2.4.2 二次函数性质的再研究 课件(共21张PPT)
文档属性
| 名称 | 2.4.2 二次函数性质的再研究 课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-07 15:04:42 | ||
图片预览




文档简介
(共21张PPT)
数学北师大
必修1
2.4
二次函数性质的再研究
在初中,我们已经学过了二次函数,知道其图像为抛物线,并了解其图像的开口方向、对称轴、顶点等特征.
下面我们进一步研究一般的二次函数
f(x)=ax2
+bx+c
(a≠0).
探究:(1)
y=x2和y=ax2
(a≠0)的图像之间有什么关系?
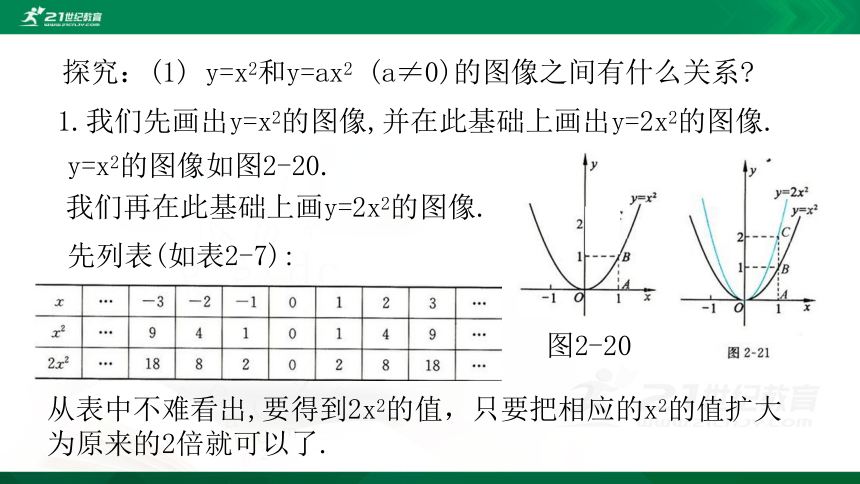
1.我们先画出y=x2的图像,并在此基础上画出y=2x2的图像.
y=x2的图像如图2-20.
我们再在此基础上画y=2x2的图像.
先列表(如表2-7):
图2-20
从表中不难看出,要得到2x2的值,只要把相应的x2的值扩大为原来的2倍就可以了.
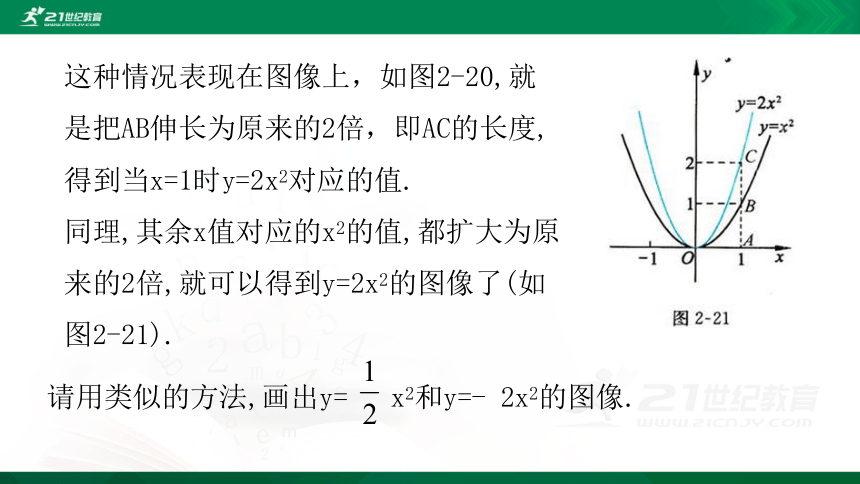
这种情况表现在图像上,如图2-20,就是把AB伸长为原来的2倍,即AC的长度,得到当x=1时y=2x2对应的值.
同理,其余x值对应的x2的值,都扩大为原来的2倍,就可以得到y=2x2的图像了(如图2-21).
请用类似的方法,画出y=
x2和y=-
2x2的图像.
二次函数y=
ax2
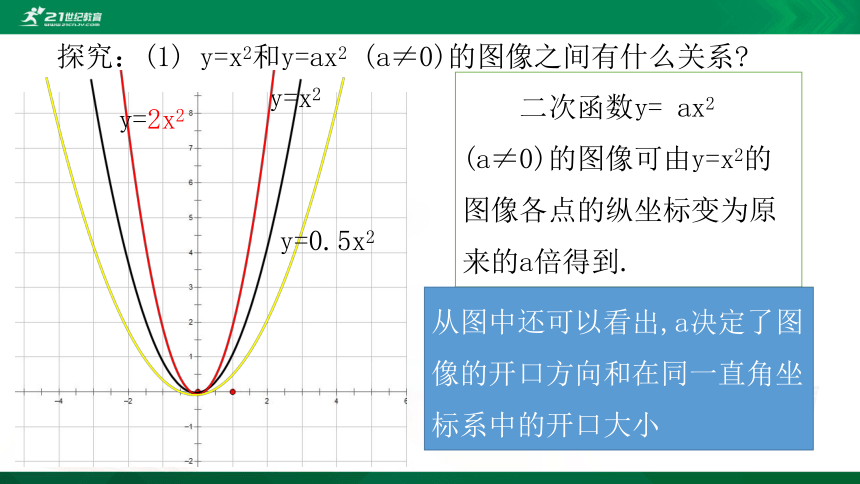
(a≠0)的图像可由y=x2的图像各点的纵坐标变为原来的a倍得到.
从图中还可以看出,a决定了图像的开口方向和在同一直角坐标系中的开口大小
探究:(1)
y=x2和y=ax2
(a≠0)的图像之间有什么关系?
y=x2
y=2x2
y=0.5x2
探究:(2)
y=ax2和y=a(x+h)2+k(a≠0)的图像之间有什么关系?
2
4
6
8
-2
-4
-6
-8
-2
-4
-6
-8
4
6
2
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
O
我们一起回顾y=2x2与y=2(x+
1)2
+3图像的关系.
在初中我们已经知道,只要把y=2x2的图像向左平移1个单位长度,【y=2(x+1)2
】再向上平移3个单位长度,
就可以得到y=2(x+1)2+3的图像.它们形状相同,位置不同
(如图2-22).
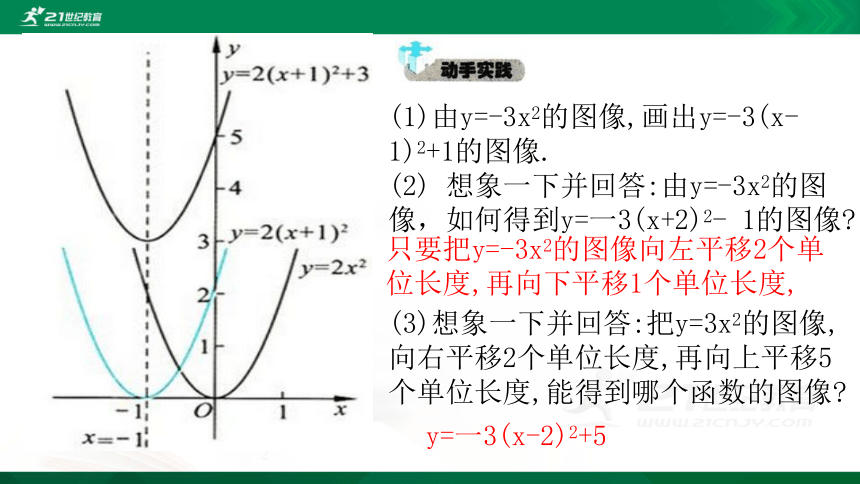
(1)由y=-3x2的图像,画出y=-3(x-
1)2+1的图像.
(2)
想象一下并回答:由y=-3x2的图像,如何得到y=一3(x+2)2-
1的图像?
(3)想象一下并回答:把y=3x2的图像,向右平移2个单位长度,再向上平移5个单位长度,能得到哪个函数的图像?
只要把y=-3x2的图像向左平移2个单位长度,再向下平移1个单位长度,
y=一3(x-2)2+5
一般地,二次函数
y=a(x+h)2+k(a≠0),
a决定了二次函数图像的开口大小及方向;
h决定了二次函数图像的左右平移,而且“h正左移,h负右移”;
k决定了二次函数图像的上下平移,而且“k正上移,k负下移”。
(2)
y=ax2和y=a(x+h)2+k(a≠0)的图像之间有什么关系?
(3)
y=ax2和y=ax2
+bx
+c(a≠0)的图像之间有什么关系?
3.我们再一起回顾一下y=2x2与y=2x2
+4x-1图像的关系.我们在初中时就知道,为研究y=2x2
+4x-
1的图像,应该通过配方把它化成我们已经掌握的y=a(x+h)2+k的形式,
即y=
2x2+4x-
1=
2(x2+2x)-
1=
2(x2+2x+1-
1)-
1=
2[(x+
1)2-
1]-
1=2(x+1)2-
3.
至此,我们就知道,把y=2x2的图像左移1个单位长度,再下移3个单位长度,就可得到y=2x2
+4x-1的图像(如图2-23).
(3)
y=ax2和y=ax2
+bx
+c(a≠0)的图像之间有什么关系?
一般地,二次函数
y=ax2
+bx+c(a≠0)
,通过配方可以得到它的恒等形式y=a(x
+h)2+k,
从而知道,由y=ax2的图像如何平移就得到它(y=ax2
+bx
+c(a≠0))的图像.
上面,我们经历了y=x2到y=ax2
,y=ax2到y=a(x+h)2+k,y=ax2到y=ax2
+bx
+c(其中,a均不为0)的图像变化过程.通过这个过程,我们就能体会到研究一般函数图像的拓展过程.
例1二次函数
f(x)与g(x)的图像开口大小相同,开口方向也相同,已知函数g(x)的解析式和f(x)图像的顶点,写出函数f(x)的解析式:
(1)函数g(x)=x2,
f(x)图像的顶点是(4,
-7);
(2)函数g(x)=-
2(x+1)2
,f(x)图像的顶点是(一3,
2).
解
如果二次函数的图像与
y=ax2的图像开口大小相同,开口方向也相同,顶点坐标是(-h,
k),则其解析式为y=a(x+h)2+k.
(1)因为f(x)与g(x)=x2的图像开口大小相同,开口方向也相同,f(x)图像的顶点是(4,-7),
所以f(x)=(x-4)2-7=x2-8x+9;
(2)因为f(x)与g(x)=-2(x+1)2的图像开口大小相同,开口方向也相同,g(x)=-2(x+1)2又与y=-2x2的图像开口大小相同,开口方向也相同,所以f(x)与y=-2x2的图像开口大小也相同,开口方向也相同.
又因为f(x)图像的顶点是(一3,
2),
所以f(x)=-2(x+3)2+2=-2x2-
12x-
16.
例1二次函数
f(x)与g(x)的图像开口大小相同,开口方向也相同,已知函数g(x)的解析式和f
(x)图像的顶点,写出函数f(x)的解析式:
(1)函数g(x)=x2,
f(x)图像的顶点是(4,
-7);
(2)函数g(x)=-
2(x+1)2
,f(x)图像的顶点是(一3,
2).
知识小结
一般地,二次函数
y=a(x+h)2+k(a≠0),
a决定了二次函数图像的开口大小及方向;
h决定了二次函数图像的左右平移,而且“h正左移,h负右移”;
k决定了二次函数图像的上下平移,而且“k正上移,k负下移”。
y=ax2和y=a(x+h)2+k(a≠0)的图像之间关系
作业:已知二次函数f(x)满足f(2)=-1,f(-1)=-1,且f(x)的最大值是8,求此二次函数的解析式.
作业:已知二次函数f(x)满足f(2)=-1,f(-1)=-1,且f(x)的最大值是8,求此二次函数的解析式.
作业:已知二次函数f(x)满足f(2)=-1,f(-1)=-1,且f(x)的最大值是8,求此二次函数的解析式.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
数学北师大
必修1
2.4
二次函数性质的再研究
在初中,我们已经学过了二次函数,知道其图像为抛物线,并了解其图像的开口方向、对称轴、顶点等特征.
下面我们进一步研究一般的二次函数
f(x)=ax2
+bx+c
(a≠0).
探究:(1)
y=x2和y=ax2
(a≠0)的图像之间有什么关系?
1.我们先画出y=x2的图像,并在此基础上画出y=2x2的图像.
y=x2的图像如图2-20.
我们再在此基础上画y=2x2的图像.
先列表(如表2-7):
图2-20
从表中不难看出,要得到2x2的值,只要把相应的x2的值扩大为原来的2倍就可以了.
这种情况表现在图像上,如图2-20,就是把AB伸长为原来的2倍,即AC的长度,得到当x=1时y=2x2对应的值.
同理,其余x值对应的x2的值,都扩大为原来的2倍,就可以得到y=2x2的图像了(如图2-21).
请用类似的方法,画出y=
x2和y=-
2x2的图像.
二次函数y=
ax2
(a≠0)的图像可由y=x2的图像各点的纵坐标变为原来的a倍得到.
从图中还可以看出,a决定了图像的开口方向和在同一直角坐标系中的开口大小
探究:(1)
y=x2和y=ax2
(a≠0)的图像之间有什么关系?
y=x2
y=2x2
y=0.5x2
探究:(2)
y=ax2和y=a(x+h)2+k(a≠0)的图像之间有什么关系?
2
4
6
8
-2
-4
-6
-8
-2
-4
-6
-8
4
6
2
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
O
我们一起回顾y=2x2与y=2(x+
1)2
+3图像的关系.
在初中我们已经知道,只要把y=2x2的图像向左平移1个单位长度,【y=2(x+1)2
】再向上平移3个单位长度,
就可以得到y=2(x+1)2+3的图像.它们形状相同,位置不同
(如图2-22).
(1)由y=-3x2的图像,画出y=-3(x-
1)2+1的图像.
(2)
想象一下并回答:由y=-3x2的图像,如何得到y=一3(x+2)2-
1的图像?
(3)想象一下并回答:把y=3x2的图像,向右平移2个单位长度,再向上平移5个单位长度,能得到哪个函数的图像?
只要把y=-3x2的图像向左平移2个单位长度,再向下平移1个单位长度,
y=一3(x-2)2+5
一般地,二次函数
y=a(x+h)2+k(a≠0),
a决定了二次函数图像的开口大小及方向;
h决定了二次函数图像的左右平移,而且“h正左移,h负右移”;
k决定了二次函数图像的上下平移,而且“k正上移,k负下移”。
(2)
y=ax2和y=a(x+h)2+k(a≠0)的图像之间有什么关系?
(3)
y=ax2和y=ax2
+bx
+c(a≠0)的图像之间有什么关系?
3.我们再一起回顾一下y=2x2与y=2x2
+4x-1图像的关系.我们在初中时就知道,为研究y=2x2
+4x-
1的图像,应该通过配方把它化成我们已经掌握的y=a(x+h)2+k的形式,
即y=
2x2+4x-
1=
2(x2+2x)-
1=
2(x2+2x+1-
1)-
1=
2[(x+
1)2-
1]-
1=2(x+1)2-
3.
至此,我们就知道,把y=2x2的图像左移1个单位长度,再下移3个单位长度,就可得到y=2x2
+4x-1的图像(如图2-23).
(3)
y=ax2和y=ax2
+bx
+c(a≠0)的图像之间有什么关系?
一般地,二次函数
y=ax2
+bx+c(a≠0)
,通过配方可以得到它的恒等形式y=a(x
+h)2+k,
从而知道,由y=ax2的图像如何平移就得到它(y=ax2
+bx
+c(a≠0))的图像.
上面,我们经历了y=x2到y=ax2
,y=ax2到y=a(x+h)2+k,y=ax2到y=ax2
+bx
+c(其中,a均不为0)的图像变化过程.通过这个过程,我们就能体会到研究一般函数图像的拓展过程.
例1二次函数
f(x)与g(x)的图像开口大小相同,开口方向也相同,已知函数g(x)的解析式和f(x)图像的顶点,写出函数f(x)的解析式:
(1)函数g(x)=x2,
f(x)图像的顶点是(4,
-7);
(2)函数g(x)=-
2(x+1)2
,f(x)图像的顶点是(一3,
2).
解
如果二次函数的图像与
y=ax2的图像开口大小相同,开口方向也相同,顶点坐标是(-h,
k),则其解析式为y=a(x+h)2+k.
(1)因为f(x)与g(x)=x2的图像开口大小相同,开口方向也相同,f(x)图像的顶点是(4,-7),
所以f(x)=(x-4)2-7=x2-8x+9;
(2)因为f(x)与g(x)=-2(x+1)2的图像开口大小相同,开口方向也相同,g(x)=-2(x+1)2又与y=-2x2的图像开口大小相同,开口方向也相同,所以f(x)与y=-2x2的图像开口大小也相同,开口方向也相同.
又因为f(x)图像的顶点是(一3,
2),
所以f(x)=-2(x+3)2+2=-2x2-
12x-
16.
例1二次函数
f(x)与g(x)的图像开口大小相同,开口方向也相同,已知函数g(x)的解析式和f
(x)图像的顶点,写出函数f(x)的解析式:
(1)函数g(x)=x2,
f(x)图像的顶点是(4,
-7);
(2)函数g(x)=-
2(x+1)2
,f(x)图像的顶点是(一3,
2).
知识小结
一般地,二次函数
y=a(x+h)2+k(a≠0),
a决定了二次函数图像的开口大小及方向;
h决定了二次函数图像的左右平移,而且“h正左移,h负右移”;
k决定了二次函数图像的上下平移,而且“k正上移,k负下移”。
y=ax2和y=a(x+h)2+k(a≠0)的图像之间关系
作业:已知二次函数f(x)满足f(2)=-1,f(-1)=-1,且f(x)的最大值是8,求此二次函数的解析式.
作业:已知二次函数f(x)满足f(2)=-1,f(-1)=-1,且f(x)的最大值是8,求此二次函数的解析式.
作业:已知二次函数f(x)满足f(2)=-1,f(-1)=-1,且f(x)的最大值是8,求此二次函数的解析式.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
