2.4.1 二次函数图象 课件(共16张PPT)
文档属性
| 名称 | 2.4.1 二次函数图象 课件(共16张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-07 15:01:12 | ||
图片预览





文档简介
(共16张PPT)
数学北师大
必修1
2.4.1
二次函数图象
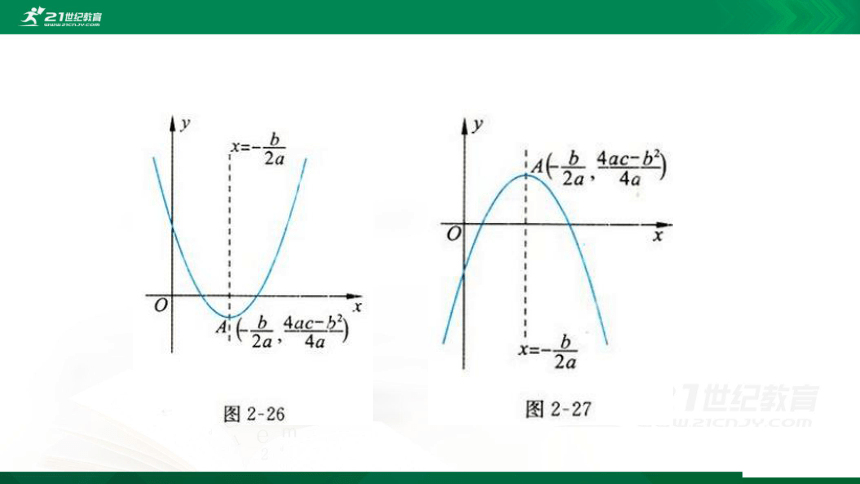
二次函数f(x)=ax2+bx+c(a≠0)的性质,主要包括图像的开口方向、顶点坐标、对称轴、单调区间、最大值和最小值.
对于二次函数f(x)=ax2+bx+c=a(x+
)2+
当a>0时,它的图像开口向上,顶点坐标为(
,
)
对称轴为直线x=
f(x)在(-∞,
)上是减少的
f(x)在(
,
+∞
)上是增加的
当:x=
,时,函数取得最小值
二次函数f(x)=ax2+bx+c(a≠0)的性质,主要包括图像的开口方向、顶点坐标、对称轴、单调区间、最大值和最小值.
对于二次函数f(x)=ax2+bx+c=a(x+
)2+
当a<0时,它的图像开口向下,顶点坐标为(
,
)
对称轴为直线x=
f(x)在(-∞,
)上是增加的
f(x)在(
,
+∞
)上是减少的
当:x=
,时,函数取得最大值
上述性质可以分别通过图2-26和图2-27直观地表示出来,也能够进行证明.下面,就其中a>0时函数的单调性进行证明.
证明:设a>0,任取x1
,x2
,且
x1
,则
f(x1)一f(x2)=
(ax22+bx2+c)-(ax12
+bx1+c)
=a(x22-x12)+b(x2-x1)=(ax2+ax1+b)(x2-x1)
<
(a×
+a×
+b)(x2-x1)<0
∴f(x1)一f(x2)<0
x2-x1>0
∴f(x1)∴f(x)在(-∞,
)上是减少的
f(x)在(
,
+∞)上是增加的
同理可证
之后我们就可以通讨a,
和
直接得到函数的主要
显然,将f(x)=ax2+bx+c配方成
f(x)=a(x+
)2+
性质,并且可以依此画出函数图像.
例2将函数y=—3x2-6x+1配方,确定其对称轴,顶点坐标,求出它的单调区间及最大值或最小值,并画出它的图像.
解:y=—3x2-6x+1=-3(x+1)2+4
由于x2的系数是负数,所以函数图像开口向下;
顶点坐标为(-1,4);
对称轴为直线x+1=0(或x=—1);
函数在区间(-∞,-1]上是增加的,
在区间[一1,+∞)上是减少的;
函数有最大值,没有最小值,函数的最大值是4.
采用描点画图,选顶点A(-
1,4),与x轴的交点B(
,o)和c(
,0),与y轴的交点D(0,1),再任取点E(—2,1),
过这5个点画出图像,如图2-28.
从这个例题中可以看出,根据配方后得到的性质画函数图像,可以直接选出关键点,减少了选点的盲目性,使画图的操作更简便,使图像更精确.
例3绿缘商店每月按出厂价每瓶3元购进一种饮料.根据以前的统计数据,若零售价定为每瓶4元,每月可销售400瓶;若每瓶售价每降低0.05元,则可多销售40瓶.在每月的进货量当月销售完的前提下,请你给该商店设计一个方案:销售价应定为多少元和从工厂购进多少瓶时,才可获得最大的利润?
解:设销售价为x元/瓶(x>3),则根据题意(销售量等于进货量),正好当月销售完的进货量为
即400(9-2x)瓶.
此时所得的利润为f(x)=400(9-2x)(x—3)
=400(-2x2+15x—27)(元).
根据函数性质,当x=3.75时,
f(x)取得最大值450.
这时进货量为400(9-2x)=400(9-2×=600(瓶).
故销售价为3.75元、购进600瓶时可获得最大利润为450元.
3.已知函数f(x)=ax2-2ax+2+b(a≠0)在[2,3]上有最大值5和最小值2,求a,b的值.
解:f(x)=ax2-2ax+2+b=a(x-1)2+2+b-a的对称轴方程是x=1.
(1)当a>0时,f(x)在[2,3]上是增函数.
求二次函数f(x)=ax2+bx+c在[m,n]上的最值或值域的一般方法是:
(1)检查x0=
是否属于
[
m,n];
(2)当x0∈[m,n]时,f(m),f(n),f(x0)
中的较大者是最大值,较小者是最小值;
(3)当x0
[m,n]时,f(m),f(n)中的较大
者是最大值,较小者是最小值.
课堂小结
3.如果函数f(x)=(x-1)2+1定义在区间[t,t+1]上,求f(x)的最小值.
图1
图2
图3
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
数学北师大
必修1
2.4.1
二次函数图象
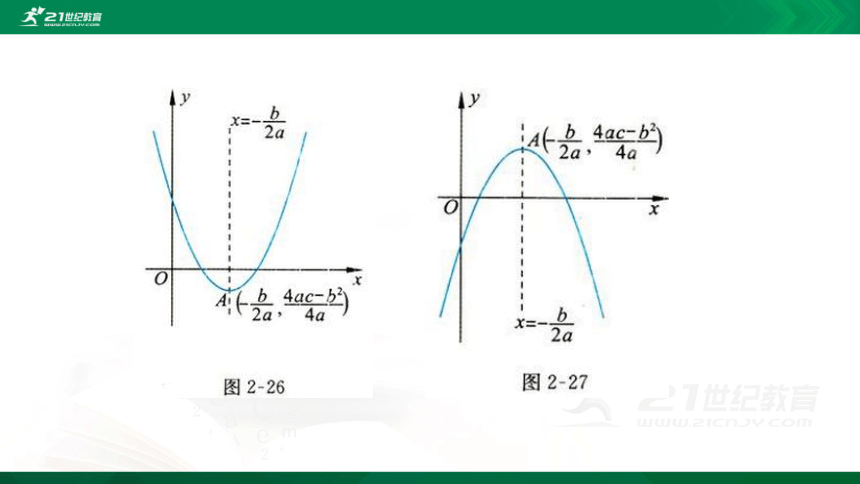
二次函数f(x)=ax2+bx+c(a≠0)的性质,主要包括图像的开口方向、顶点坐标、对称轴、单调区间、最大值和最小值.
对于二次函数f(x)=ax2+bx+c=a(x+
)2+
当a>0时,它的图像开口向上,顶点坐标为(
,
)
对称轴为直线x=
f(x)在(-∞,
)上是减少的
f(x)在(
,
+∞
)上是增加的
当:x=
,时,函数取得最小值
二次函数f(x)=ax2+bx+c(a≠0)的性质,主要包括图像的开口方向、顶点坐标、对称轴、单调区间、最大值和最小值.
对于二次函数f(x)=ax2+bx+c=a(x+
)2+
当a<0时,它的图像开口向下,顶点坐标为(
,
)
对称轴为直线x=
f(x)在(-∞,
)上是增加的
f(x)在(
,
+∞
)上是减少的
当:x=
,时,函数取得最大值
上述性质可以分别通过图2-26和图2-27直观地表示出来,也能够进行证明.下面,就其中a>0时函数的单调性进行证明.
证明:设a>0,任取x1
,x2
,且
x1
f(x1)一f(x2)=
(ax22+bx2+c)-(ax12
+bx1+c)
=a(x22-x12)+b(x2-x1)=(ax2+ax1+b)(x2-x1)
<
(a×
+a×
+b)(x2-x1)<0
∴f(x1)一f(x2)<0
x2-x1>0
∴f(x1)
)上是减少的
f(x)在(
,
+∞)上是增加的
同理可证
之后我们就可以通讨a,
和
直接得到函数的主要
显然,将f(x)=ax2+bx+c配方成
f(x)=a(x+
)2+
性质,并且可以依此画出函数图像.
例2将函数y=—3x2-6x+1配方,确定其对称轴,顶点坐标,求出它的单调区间及最大值或最小值,并画出它的图像.
解:y=—3x2-6x+1=-3(x+1)2+4
由于x2的系数是负数,所以函数图像开口向下;
顶点坐标为(-1,4);
对称轴为直线x+1=0(或x=—1);
函数在区间(-∞,-1]上是增加的,
在区间[一1,+∞)上是减少的;
函数有最大值,没有最小值,函数的最大值是4.
采用描点画图,选顶点A(-
1,4),与x轴的交点B(
,o)和c(
,0),与y轴的交点D(0,1),再任取点E(—2,1),
过这5个点画出图像,如图2-28.
从这个例题中可以看出,根据配方后得到的性质画函数图像,可以直接选出关键点,减少了选点的盲目性,使画图的操作更简便,使图像更精确.
例3绿缘商店每月按出厂价每瓶3元购进一种饮料.根据以前的统计数据,若零售价定为每瓶4元,每月可销售400瓶;若每瓶售价每降低0.05元,则可多销售40瓶.在每月的进货量当月销售完的前提下,请你给该商店设计一个方案:销售价应定为多少元和从工厂购进多少瓶时,才可获得最大的利润?
解:设销售价为x元/瓶(x>3),则根据题意(销售量等于进货量),正好当月销售完的进货量为
即400(9-2x)瓶.
此时所得的利润为f(x)=400(9-2x)(x—3)
=400(-2x2+15x—27)(元).
根据函数性质,当x=3.75时,
f(x)取得最大值450.
这时进货量为400(9-2x)=400(9-2×=600(瓶).
故销售价为3.75元、购进600瓶时可获得最大利润为450元.
3.已知函数f(x)=ax2-2ax+2+b(a≠0)在[2,3]上有最大值5和最小值2,求a,b的值.
解:f(x)=ax2-2ax+2+b=a(x-1)2+2+b-a的对称轴方程是x=1.
(1)当a>0时,f(x)在[2,3]上是增函数.
求二次函数f(x)=ax2+bx+c在[m,n]上的最值或值域的一般方法是:
(1)检查x0=
是否属于
[
m,n];
(2)当x0∈[m,n]时,f(m),f(n),f(x0)
中的较大者是最大值,较小者是最小值;
(3)当x0
[m,n]时,f(m),f(n)中的较大
者是最大值,较小者是最小值.
课堂小结
3.如果函数f(x)=(x-1)2+1定义在区间[t,t+1]上,求f(x)的最小值.
图1
图2
图3
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
