人教版八上高分笔记之导与练11章 三角形章末整合(原卷+答案)
文档属性
| 名称 | 人教版八上高分笔记之导与练11章 三角形章末整合(原卷+答案) |  | |
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-05 20:57:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第11章
三角形
本章学习的主要知识有三角形和多边形,其中三角形中主要学习了与三角形有关的线段和三角形内角、外角相关的知识,多边形中主要学习了多边形的内角和与外角和,一般考查的内容包括三角形的计数,三角形的三边关系,三角形的中线、高、角平分线,三角形的内角和及外角性质,多边形的内角和与外角和等.本章热门考点可概括为两个概念、三种线段、三个关系、两种计算、两个技巧和三种思想。
考点1?两个概念
概念1?与三角形有关的概念
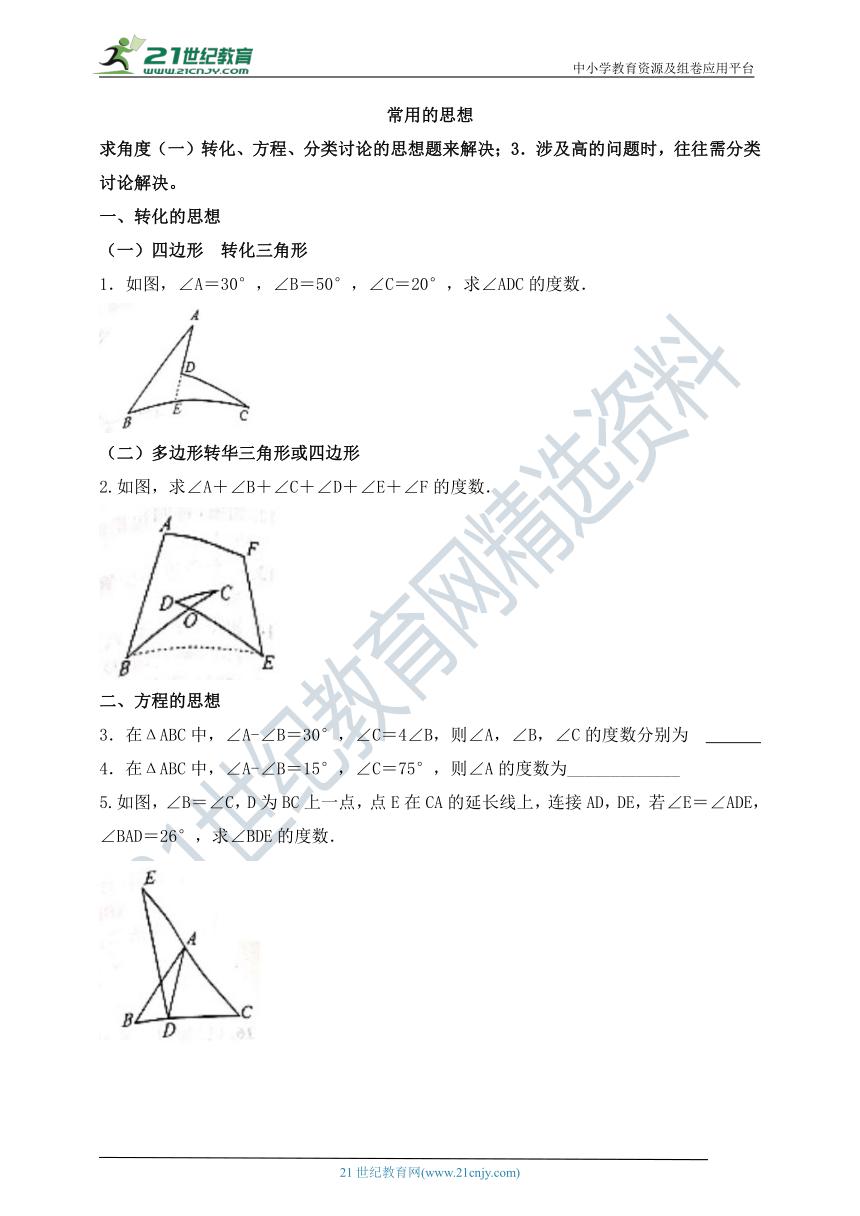
1.如图,图中有8个三角形;其中以AB为边的三角形为
??;以∠OCB为内角的三角形为?
;在ΔBOC中,OC所对的角是
,∠OCB所对的边是?
.
概念2
与多边形有关的概念
下列说法正确的是?(
)
A.由一些线段首尾顺次相接组成的图形叫做多边形
B.多边形的两边所在直线组成的角是这个多边形的内角或外角
C.各个角都相等,各条边都相等的多边形是正多边形
D.连接多边形的两个顶点的线段,叫做多边形的对角线
考点二
三种线段
如图,AD,CE是ΔABC的两条高,AB=4cm,BC=8cm,CE=6cm,则AD的长为?
3题
4题
4.在△ABC中,E是边BC上的一点,EC=2BE,点D是AC的中点,连接AE,BD交于点F,若S△ABC=12,则S△ADF-S△BEF=___
___
5.如图,在ΔABC中,AF是中线,AE是角平分线,AD是高,∠BAC=90°,FC=6.根据图形填空:
(1)BF=
,?BC=
;?
(2)∠BAE=
,?
∠CAE=
;?
(3)∠ADB=??
,∠ADC=?
?
考点3?三个关系
关系1
三角形的三边关系
6.已知三角形的两边长分别为1和4,第三边长为整数,则该三角形的周长为?(
)
A.7
B.8
C.9
D.10
关系2
三角形内、外角的关系
7.如图,在ΔABC中,D是BC边上的一点,∠1=∠2,∠3=∠4,∠BAC=57°.求∠CAD的度数.
关系3
多边形内、外角的关系
8.用一条足够长的和方形纸条,打一个结,然后轻轻拉紧,压平就可以得到如图所示的正五边形ABCDE,其中∠BAC=
度.
常用的思想
求角度(一)转化、方程、分类讨论的思想题来解决;3.涉及高的问题时,往往需分类讨论解决。
一、转化的思想
(一)四边形?转化三角形
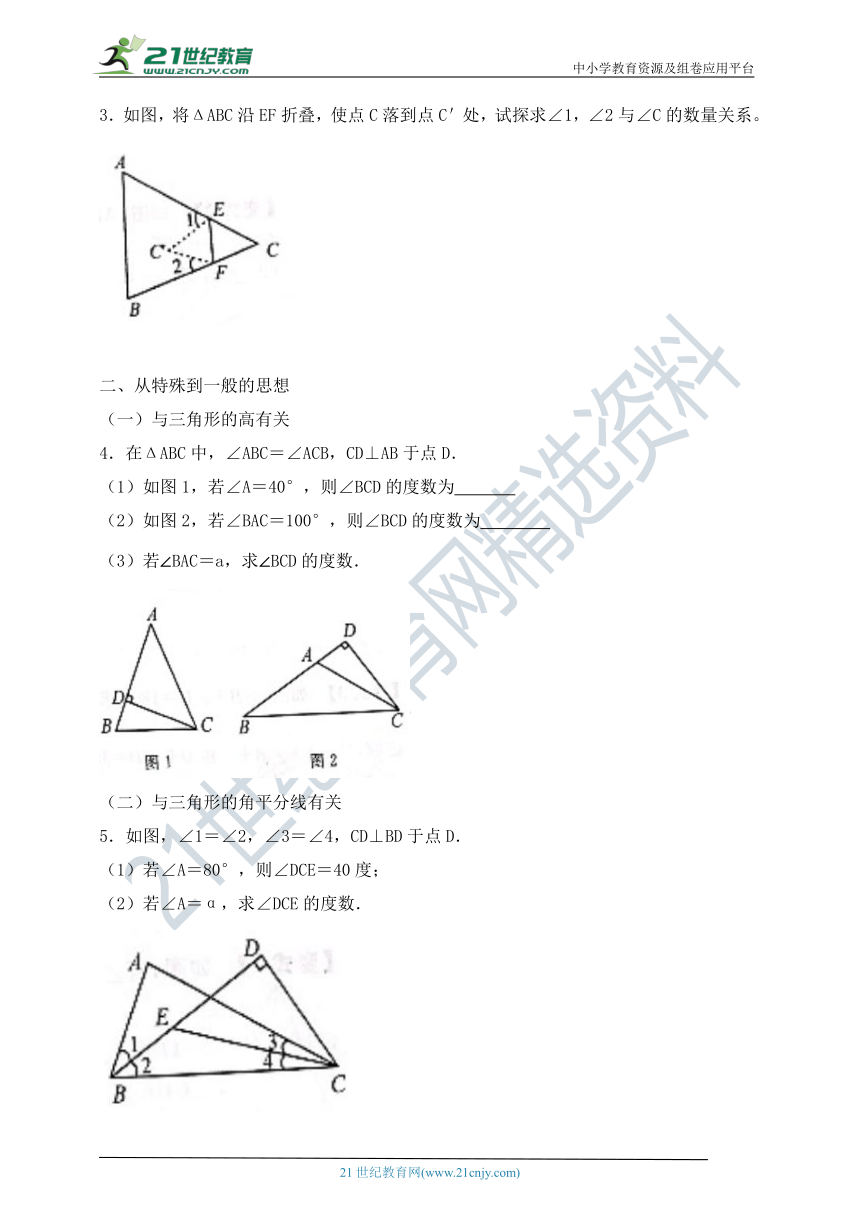
1.如图,∠A=30°,∠B=50°,∠C=20°,求∠ADC的度数.
(二)多边形转华三角形或四边形
2.如图,求∠A+∠B+∠C+∠D+∠E+∠F的度数.
二、方程的思想
3.在ΔABC中,∠A-∠B=30°,∠C=4∠B,则∠A,∠B,∠C的度数分别为??
4.在ΔABC中,∠A-∠B=15°,∠C=75°,则∠A的度数为_____________
5.如图,∠B=∠C,D为BC上一点,点E在CA的延长线上,连接AD,DE,若∠E=∠ADE,∠BAD=26°,求∠BDE的度数.
在ΔABC中,AD是高,∠BAD=60°,∠CAD=20°,AE平分∠BAC,则∠EAD的度数为
7.在ΔABC中,∠ABC=∠C,BD是AC边上的高,∠ABD=40°,求∠C的度数.
8.已知非直角ΔABC中,∠A=40°,高BD和CE所在直线交于点H,求∠BHC的度数.?
方法技巧??求角度(二)整体、从特殊到一般的思想
一、整体的思想
1.如图,∠1+∠2=70°,若∠A=60°,求∠BOC的度数。
如图,求∠A+∠B+∠C+∠D+∠E的度数.
3.如图,将ΔABC沿EF折叠,使点C落到点C'处,试探求∠1,∠2与∠C的数量关系。
从特殊到一般的思想
(一)与三角形的高有关
4.在ΔABC中,∠ABC=∠ACB,CD⊥AB于点D.
(1)如图1,若∠A=40°,则∠BCD的度数为
(2)如图2,若∠BAC=100°,则∠BCD的度数为
(3)若∠BAC=a,求∠BCD的度数.
(二)与三角形的角平分线有关
5.如图,∠1=∠2,∠3=∠4,CD⊥BD于点D.
(1)若∠A=80°,则∠DCE=40度;
(2)若∠A=α,求∠DCE的度数.
答案:考点1?两个概念
概念1?与三角形有关的概念
1.如图,图中有8个三角形;其中以AB为边的三角形为△ABO,ΔABC,ΔABD??;以∠OCB为内角的三角形为?ΔBOC,ΔABC;在ΔBOC中,OC所对的角是∠OBC,∠OCB所对的边是?OB.
概念2
与多边形有关的概念
下列说法正确的是?(
C
)
A.由一些线段首尾顺次相接组成的图形叫做多边形
B.多边形的两边所在直线组成的角是这个多边形的内角或外角
C.各个角都相等,各条边都相等的多边形是正多边形
D.连接多边形的两个顶点的线段,叫做多边形的对角线
考点二
三种线段
如图,AD,CE是ΔABC的两条高,AB=4cm,BC=8cm,CE=6cm,则AD的长为?3cm?
3题
4题
4.在△ABC中,E是边BC上的一点,EC=2BE,点D是AC的中点,连接AE,BD交于点F,若S△ABC=12,则S△ADF-S△BEF=___2___
5.如图,在ΔABC中,AF是中线,AE是角平分线,AD是高,∠BAC=90°,FC=6.根据图形填空:
(1)BF=6,?BC=12;?
(2)∠BAE=45°,?
∠CAE=45°;?
(3)∠ADB=??90°,∠ADC=?900?
考点3?三个关系
关系1
三角形的三边关系
6.已知三角形的两边长分别为1和4,第三边长为整数,则该三角形的周长为?(
C
)
A.7
B.8
C.9
D.10
关系2
三角形内、外角的关系
7.如图,在ΔABC中,D是BC边上的一点,∠1=∠2,∠3=∠4,∠BAC=57°.求∠CAD的度数.
解:设∠1=∠2=x°,则∠3=∠4=∠1+∠2=2x°.
在ΔABC中,∠2+∠4+∠BAC=180°,∠BAC=57°,?
x+2x+57=180,?
解得x=41.
∠CAD=∠BAC-∠1=57-41°=16°.?
关系3
多边形内、外角的关系
8.用一条足够长的和方形纸条,打一个结,然后轻轻拉紧,压平就可以得到如图所示的正五边形ABCDE,其中∠BAC=36度.
常用的思想?
求角度(一)转化、方程、分类讨论的思想
问题来解决;3.涉及高的问题时,往往需分类讨论解决。
一、转化的思想
(一)四边形?转化三角形
1.如图,∠A=30°,∠B=50°,∠C=20°,求∠ADC的度数.
解:∠ADC=100°.
方法一:延长AD交BC于点E.
方法二:作射线BD.
方法三:连接AC.
(二)多边形转华三角形或四边形
2.如图,求∠A+∠B+∠C+∠D+∠E+∠F的度数.
解:∠A+∠ABC+∠C+∠D+∠DEF+∠F=360°.
二、方程的思想
3.在ΔABC中,∠A-∠B=30°,∠C=4∠B,则∠A,∠B,∠C的度数分别为??55°,25°,100°60°
4.在ΔABC中,∠A-∠B=15°,∠C=75°,则∠A的度数为__600____
5.如图,∠B=∠C,D为BC上一点,点E在CA的延长线上,连接AD,DE,若∠E=∠ADE,∠BAD=26°,求∠BDE的度数.
解:设∠E=∠ADE=a,∴∠CAD=2a,
∵∠BAD=26°,∠BAC=2α+26°,
∵∠B=∠C,.∴∠C=77°-α,
∵∠BDE=∠C+∠E,∴∠BDE=77°.
三、分类讨论的思想
6.在ΔABC中,AD是高,∠BAD=60°,∠CAD=20°,AE平分∠BAC,则∠EAD的度数为20°或40°
解:当高AD在ΔABC内部时,∠EAD=20°;
当高AD在ΔABC外部时,∠EAD=40°.
7.在ΔABC中,∠ABC=∠C,BD是AC边上的高,∠ABD=40°,求∠C的度数.
解:①∠BAC为锐角时,∠C=65°;
②∠BAC为钝角时,∠C=25°.
8.已知非直角ΔABC中,∠A=40°,高BD和CE所在直线交于点H,求∠BHC的度数.?
解:①∠ACB为锐角时,∠BHC=140°;
②∠ACB为钝角时,∠BHC=40°;
③∠ABC为钝角时,∠BHC=40°.?
方法技巧??求角度(二)整体、从特殊到一般的思想
一、整体的思想
1.如图,∠1+∠2=70°,若∠A=60°,求∠BOC的度数。
解:130°.
如图,求∠A+∠B+∠C+∠D+∠E的度数.
解:180°,方法一:∠C+∠D=∠BPC,∠BFC+∠B=∠EGA,
∠A+∠EGA+∠E=180°;?
方法二:连接AB:∠C+∠D=∠FAB+∠FBA.
3.如图,将ΔABC沿EF折叠,使点C落到点C'处,试探求∠1,∠2与∠C的数量关系。
解:∠1=180°-2∠CEF,∠2=180°-2∠CFE,
∴∠1+∠2=360°-2(∠CEF+∠CFE)=360°-2(180°-∠C)?
=360°-360°+2∠C=2∠C.?
从特殊到一般的思想
(一)与三角形的高有关
4.在ΔABC中,∠ABC=∠ACB,CD⊥AB于点D.
(1)如图1,若∠A=40°,则∠BCD的度数为20°
(2)如图2,若∠BAC=100°,则∠BCD的度数为50°
(3)若∠BAC=a,求∠BCD的度数.
解:(1)20°;(2)50°;(3)α.
(二)与三角形的角平分线有关
5.如图,∠1=∠2,∠3=∠4,CD⊥BD于点D.
(1)若∠A=80°,则∠DCE=40度;
(2)若∠A=α,求∠DCE的度数.
解:(1)40;
易证:∠BEC=900-∠A
∴∠DCE=∠BEC-900=900+∠A-900=∠A
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
第11章
三角形
本章学习的主要知识有三角形和多边形,其中三角形中主要学习了与三角形有关的线段和三角形内角、外角相关的知识,多边形中主要学习了多边形的内角和与外角和,一般考查的内容包括三角形的计数,三角形的三边关系,三角形的中线、高、角平分线,三角形的内角和及外角性质,多边形的内角和与外角和等.本章热门考点可概括为两个概念、三种线段、三个关系、两种计算、两个技巧和三种思想。
考点1?两个概念
概念1?与三角形有关的概念
1.如图,图中有8个三角形;其中以AB为边的三角形为
??;以∠OCB为内角的三角形为?
;在ΔBOC中,OC所对的角是
,∠OCB所对的边是?
.
概念2
与多边形有关的概念
下列说法正确的是?(
)
A.由一些线段首尾顺次相接组成的图形叫做多边形
B.多边形的两边所在直线组成的角是这个多边形的内角或外角
C.各个角都相等,各条边都相等的多边形是正多边形
D.连接多边形的两个顶点的线段,叫做多边形的对角线
考点二
三种线段
如图,AD,CE是ΔABC的两条高,AB=4cm,BC=8cm,CE=6cm,则AD的长为?
3题
4题
4.在△ABC中,E是边BC上的一点,EC=2BE,点D是AC的中点,连接AE,BD交于点F,若S△ABC=12,则S△ADF-S△BEF=___
___
5.如图,在ΔABC中,AF是中线,AE是角平分线,AD是高,∠BAC=90°,FC=6.根据图形填空:
(1)BF=
,?BC=
;?
(2)∠BAE=
,?
∠CAE=
;?
(3)∠ADB=??
,∠ADC=?
?
考点3?三个关系
关系1
三角形的三边关系
6.已知三角形的两边长分别为1和4,第三边长为整数,则该三角形的周长为?(
)
A.7
B.8
C.9
D.10
关系2
三角形内、外角的关系
7.如图,在ΔABC中,D是BC边上的一点,∠1=∠2,∠3=∠4,∠BAC=57°.求∠CAD的度数.
关系3
多边形内、外角的关系
8.用一条足够长的和方形纸条,打一个结,然后轻轻拉紧,压平就可以得到如图所示的正五边形ABCDE,其中∠BAC=
度.
常用的思想
求角度(一)转化、方程、分类讨论的思想题来解决;3.涉及高的问题时,往往需分类讨论解决。
一、转化的思想
(一)四边形?转化三角形
1.如图,∠A=30°,∠B=50°,∠C=20°,求∠ADC的度数.
(二)多边形转华三角形或四边形
2.如图,求∠A+∠B+∠C+∠D+∠E+∠F的度数.
二、方程的思想
3.在ΔABC中,∠A-∠B=30°,∠C=4∠B,则∠A,∠B,∠C的度数分别为??
4.在ΔABC中,∠A-∠B=15°,∠C=75°,则∠A的度数为_____________
5.如图,∠B=∠C,D为BC上一点,点E在CA的延长线上,连接AD,DE,若∠E=∠ADE,∠BAD=26°,求∠BDE的度数.
在ΔABC中,AD是高,∠BAD=60°,∠CAD=20°,AE平分∠BAC,则∠EAD的度数为
7.在ΔABC中,∠ABC=∠C,BD是AC边上的高,∠ABD=40°,求∠C的度数.
8.已知非直角ΔABC中,∠A=40°,高BD和CE所在直线交于点H,求∠BHC的度数.?
方法技巧??求角度(二)整体、从特殊到一般的思想
一、整体的思想
1.如图,∠1+∠2=70°,若∠A=60°,求∠BOC的度数。
如图,求∠A+∠B+∠C+∠D+∠E的度数.
3.如图,将ΔABC沿EF折叠,使点C落到点C'处,试探求∠1,∠2与∠C的数量关系。
从特殊到一般的思想
(一)与三角形的高有关
4.在ΔABC中,∠ABC=∠ACB,CD⊥AB于点D.
(1)如图1,若∠A=40°,则∠BCD的度数为
(2)如图2,若∠BAC=100°,则∠BCD的度数为
(3)若∠BAC=a,求∠BCD的度数.
(二)与三角形的角平分线有关
5.如图,∠1=∠2,∠3=∠4,CD⊥BD于点D.
(1)若∠A=80°,则∠DCE=40度;
(2)若∠A=α,求∠DCE的度数.
答案:考点1?两个概念
概念1?与三角形有关的概念
1.如图,图中有8个三角形;其中以AB为边的三角形为△ABO,ΔABC,ΔABD??;以∠OCB为内角的三角形为?ΔBOC,ΔABC;在ΔBOC中,OC所对的角是∠OBC,∠OCB所对的边是?OB.
概念2
与多边形有关的概念
下列说法正确的是?(
C
)
A.由一些线段首尾顺次相接组成的图形叫做多边形
B.多边形的两边所在直线组成的角是这个多边形的内角或外角
C.各个角都相等,各条边都相等的多边形是正多边形
D.连接多边形的两个顶点的线段,叫做多边形的对角线
考点二
三种线段
如图,AD,CE是ΔABC的两条高,AB=4cm,BC=8cm,CE=6cm,则AD的长为?3cm?
3题
4题
4.在△ABC中,E是边BC上的一点,EC=2BE,点D是AC的中点,连接AE,BD交于点F,若S△ABC=12,则S△ADF-S△BEF=___2___
5.如图,在ΔABC中,AF是中线,AE是角平分线,AD是高,∠BAC=90°,FC=6.根据图形填空:
(1)BF=6,?BC=12;?
(2)∠BAE=45°,?
∠CAE=45°;?
(3)∠ADB=??90°,∠ADC=?900?
考点3?三个关系
关系1
三角形的三边关系
6.已知三角形的两边长分别为1和4,第三边长为整数,则该三角形的周长为?(
C
)
A.7
B.8
C.9
D.10
关系2
三角形内、外角的关系
7.如图,在ΔABC中,D是BC边上的一点,∠1=∠2,∠3=∠4,∠BAC=57°.求∠CAD的度数.
解:设∠1=∠2=x°,则∠3=∠4=∠1+∠2=2x°.
在ΔABC中,∠2+∠4+∠BAC=180°,∠BAC=57°,?
x+2x+57=180,?
解得x=41.
∠CAD=∠BAC-∠1=57-41°=16°.?
关系3
多边形内、外角的关系
8.用一条足够长的和方形纸条,打一个结,然后轻轻拉紧,压平就可以得到如图所示的正五边形ABCDE,其中∠BAC=36度.
常用的思想?
求角度(一)转化、方程、分类讨论的思想
问题来解决;3.涉及高的问题时,往往需分类讨论解决。
一、转化的思想
(一)四边形?转化三角形
1.如图,∠A=30°,∠B=50°,∠C=20°,求∠ADC的度数.
解:∠ADC=100°.
方法一:延长AD交BC于点E.
方法二:作射线BD.
方法三:连接AC.
(二)多边形转华三角形或四边形
2.如图,求∠A+∠B+∠C+∠D+∠E+∠F的度数.
解:∠A+∠ABC+∠C+∠D+∠DEF+∠F=360°.
二、方程的思想
3.在ΔABC中,∠A-∠B=30°,∠C=4∠B,则∠A,∠B,∠C的度数分别为??55°,25°,100°60°
4.在ΔABC中,∠A-∠B=15°,∠C=75°,则∠A的度数为__600____
5.如图,∠B=∠C,D为BC上一点,点E在CA的延长线上,连接AD,DE,若∠E=∠ADE,∠BAD=26°,求∠BDE的度数.
解:设∠E=∠ADE=a,∴∠CAD=2a,
∵∠BAD=26°,∠BAC=2α+26°,
∵∠B=∠C,.∴∠C=77°-α,
∵∠BDE=∠C+∠E,∴∠BDE=77°.
三、分类讨论的思想
6.在ΔABC中,AD是高,∠BAD=60°,∠CAD=20°,AE平分∠BAC,则∠EAD的度数为20°或40°
解:当高AD在ΔABC内部时,∠EAD=20°;
当高AD在ΔABC外部时,∠EAD=40°.
7.在ΔABC中,∠ABC=∠C,BD是AC边上的高,∠ABD=40°,求∠C的度数.
解:①∠BAC为锐角时,∠C=65°;
②∠BAC为钝角时,∠C=25°.
8.已知非直角ΔABC中,∠A=40°,高BD和CE所在直线交于点H,求∠BHC的度数.?
解:①∠ACB为锐角时,∠BHC=140°;
②∠ACB为钝角时,∠BHC=40°;
③∠ABC为钝角时,∠BHC=40°.?
方法技巧??求角度(二)整体、从特殊到一般的思想
一、整体的思想
1.如图,∠1+∠2=70°,若∠A=60°,求∠BOC的度数。
解:130°.
如图,求∠A+∠B+∠C+∠D+∠E的度数.
解:180°,方法一:∠C+∠D=∠BPC,∠BFC+∠B=∠EGA,
∠A+∠EGA+∠E=180°;?
方法二:连接AB:∠C+∠D=∠FAB+∠FBA.
3.如图,将ΔABC沿EF折叠,使点C落到点C'处,试探求∠1,∠2与∠C的数量关系。
解:∠1=180°-2∠CEF,∠2=180°-2∠CFE,
∴∠1+∠2=360°-2(∠CEF+∠CFE)=360°-2(180°-∠C)?
=360°-360°+2∠C=2∠C.?
从特殊到一般的思想
(一)与三角形的高有关
4.在ΔABC中,∠ABC=∠ACB,CD⊥AB于点D.
(1)如图1,若∠A=40°,则∠BCD的度数为20°
(2)如图2,若∠BAC=100°,则∠BCD的度数为50°
(3)若∠BAC=a,求∠BCD的度数.
解:(1)20°;(2)50°;(3)α.
(二)与三角形的角平分线有关
5.如图,∠1=∠2,∠3=∠4,CD⊥BD于点D.
(1)若∠A=80°,则∠DCE=40度;
(2)若∠A=α,求∠DCE的度数.
解:(1)40;
易证:∠BEC=900-∠A
∴∠DCE=∠BEC-900=900+∠A-900=∠A
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
