福建省漳州市芗城中学2010-2011学年高二下学期期末考试数学(文)试题
文档属性
| 名称 | 福建省漳州市芗城中学2010-2011学年高二下学期期末考试数学(文)试题 |

|
|
| 格式 | zip | ||
| 文件大小 | 340.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-06-21 00:00:00 | ||
图片预览



文档简介
本试卷分第1卷(选择题)和第Ⅱ卷(非选择题).本试卷满分150分.考试时间120分钟.
第Ⅰ卷(选择题 共60分)
选择题:本大题共12小题,每题5分,共60分.在给出的四个选项中,只有一项是符合题目要求的。
1. 已知集合A={1,3,5,7,9},B={0,3,6,9,12},则A∩B=( )
A. {3,5} B. {3,6} C. {3,7} D. {3,9}
2. 命题“若一个数是负数,则它的平方是正数”的否命题是( )
A. “若一个数是正数,则它的平方不是正数”
B. “若一个数是正数,则它的平方是负数”
C. “若一个数不是负数,则它的平方不是正数”
D. “若一个数不是负数,则它的平方是负数”
3、 已知命题:,则( )
A. B.
C. D.
4. 若命题p∧q为假,且 为假,则( )
A. p或q为假 B. q假
C. q真 D. p假
5.函数在区间 上的最大值是( )
A.1 B.9 C. 27 D.
6.下列函数中,在上是减函数的是( )
A. B. C. D.
7.已知,则“”是“”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
8.方程的根所在的区间是( )
A. B. C. D.
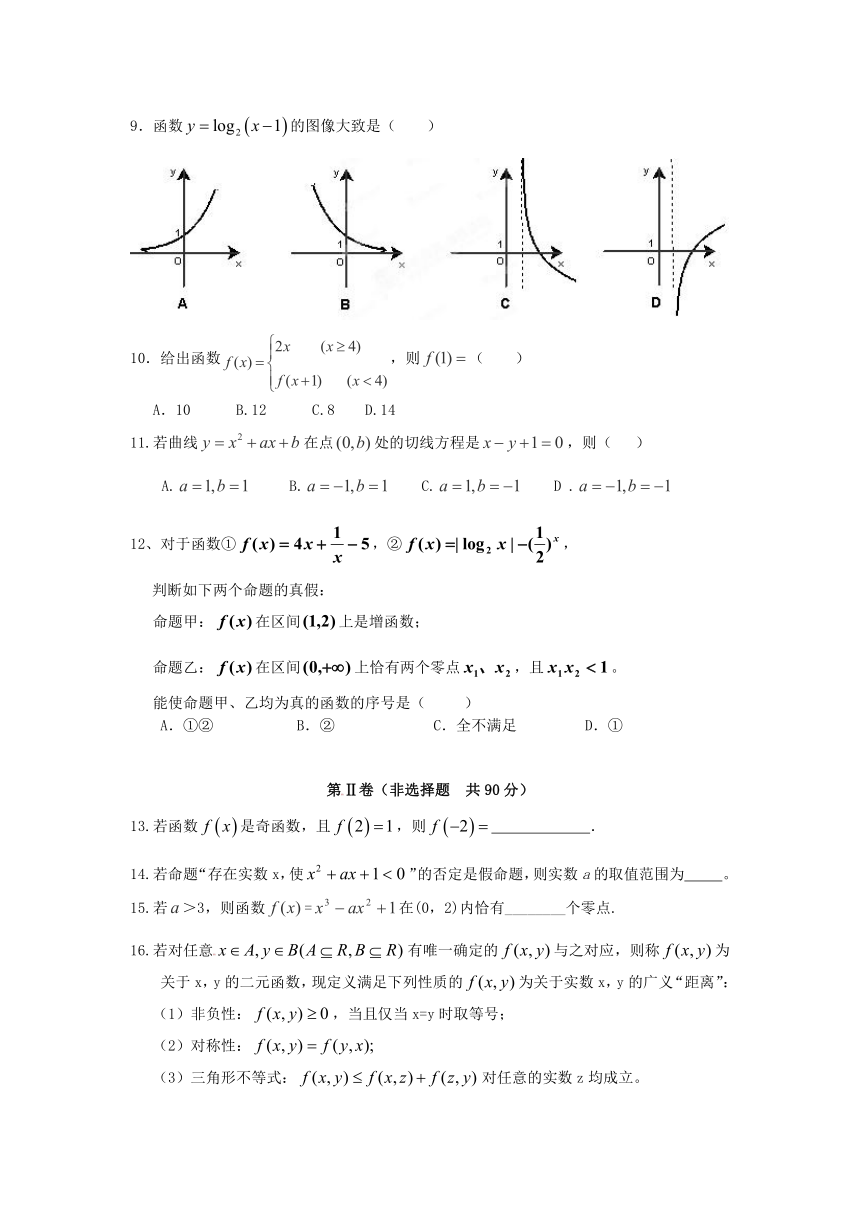
9.函数的图像大致是( )
10.给出函数,则( )
A.10 B.12 C.8 D.14
11.若曲线在点处的切线方程是,则( )
A. B. C. D .
12、对于函数①,②,
判断如下两个命题的真假:
命题甲:在区间上是增函数;
命题乙:在区间上恰有两个零点,且。
能使命题甲、乙均为真的函数的序号是( )
A.①② B.② C.全不满足 D.①
第Ⅱ卷(非选择题 共90分)
若函数是奇函数,且,则 .
若命题“存在实数x,使”的否定是假命题,则实数a的取值范围为 。
若>3,则函数=在(0,2)内恰有________个零点.
若对任意有唯一确定的与之对应,则称为关于x,y的二元函数,现定义满足下列性质的为关于实数x,y的广义“距离”:
(1)非负性:,当且仅当x=y时取等号;
(2)对称性:
(3)三角形不等式:对任意的实数z均成立。
给出三个二元函数:①②
③
则所有能够成为关于x,y的广义“距离”的序号为 。
三、解答题:17-21每题满分12分,22题满分14分.解答须写文字说明、证明过程、演算步骤.
17.设命题:函数f(x)=x3-ax-1在区间上单调递减;命题:函数的值域是.如果命题为真命题,为假命题,求的取值范围.
集合A={x|x2-2x-3≤0,x∈R},B={x|x2-2mx+m2-4≤0,x∈R,m∈R}.
(1)若A∩B=[0,3],求实数m的值;
(2)若A ,求实数m的取值范围.
19、已知是上的奇函数,且当时,,
(1)当时,的解析式 ;
求函数的零点。
20. 2010年9月5日生效的一年期个人贷款利率为7.29%,小陈准备购一部汽车,购车一年后一次性付清车款,这时某商业银行推出一种一年期优惠贷款业务,年利率为,且(0.045,0.062),贷款量与利率的平方成正比,因此,小陈申请这种一年期优惠贷款.(利息=贷款量乘以利率)
写出小陈采用优惠贷款方式贷款应支付的利息;
(2) 一年期优惠利率为多少时,两种贷款的利息差最大
21.已知关于x的二次函数f(x)=x2+(2t-1)x+1-2t.
(1)求证:对于任意t∈R,方程f(x)=1必有实数根;
(2)若<t<,求证:方程f(x)=0在区间(-1,0)及(0,)内各有一个实数根.
22.设函数(),其中.
(Ⅰ)当时,求曲线在点处的切线方程;
(Ⅱ)当时,求函数的极大值和极小值;
(Ⅲ)当时,是否存在函数图像上两点以及函数图像上两点,使得以这四点为顶点的四边形ABCD满足如下条件:四边形ABCD是平行四边形;轴;。若存在,指出四边形ABCD的个数;若不存在,说明理由。
芗城中学10-11下学期高二年期末考试卷
数学(文科)试卷答案
选择题(每题5分)
解答题(12*5+14=74)
17、
...10分
综上所述:..........12分
(2) RB={x|xm+2}........8分
A RB,∴m-2>3或m+2<-1................10分
∴m>5或m<-3..................12分
19、(本小题12分)
解:(1)当时,
则 .....2分
∵ 是的奇函数 ∴.......4分
∴当时,
……………6分
(本小题12分)
(1)由题意,贷款量为(,应支付利息=
(2)小陈的两种贷款方式的利息差为
令=0,解得或
当
所以,时,利息差取得极大值,即一年期优惠利率为4.68%时,利息差最大.
(2)当<t<时,因为f(-1)=3-4t=4(-t)>0,
f(0)=1-2t=2(-t)<0,f()=+(2t-1)+1-2t=-t>0,.........9分
f(-1)f(0)<0 , f(0)f()<0.........11分
所以方程f(x)=0在区间(-1,0)及(0,)内各有一个实数根.....12分
22.(Ⅰ)当时,,得,且,.所以,曲线在点处的切线方程是,整理得......4分
(Ⅱ)解:,.
令,解得或. .....6分
由于,以下分两种情况讨论.
(1)若,当变化时,的正负如下表:
因此,函数在处取得极小值,且;
函数在处取得极大值,且.
若,当变化时,的正负如下表:
因此,函数在处取得极小值,且;
函数在处取得极大值,且........10分
令,得或
由表格知,为的极大值,为的极大值,而 ,故的图像与x轴有且只有一个交点,有且只有一个零点。
时,,令,,
由知为的极大值,为的极大值,而
,故的图像与x轴有三个交点,有三个零点。
由知,方程有四个不同的实根,从小到大依次记为,这四个根对应的四条线段中的每两条对应一个平行四边形ABCD,共有6个,所以满足题意的平行四边形ABCD有6个。...........14分
第Ⅰ卷(选择题 共60分)
选择题:本大题共12小题,每题5分,共60分.在给出的四个选项中,只有一项是符合题目要求的。
1. 已知集合A={1,3,5,7,9},B={0,3,6,9,12},则A∩B=( )
A. {3,5} B. {3,6} C. {3,7} D. {3,9}
2. 命题“若一个数是负数,则它的平方是正数”的否命题是( )
A. “若一个数是正数,则它的平方不是正数”
B. “若一个数是正数,则它的平方是负数”
C. “若一个数不是负数,则它的平方不是正数”
D. “若一个数不是负数,则它的平方是负数”
3、 已知命题:,则( )
A. B.
C. D.
4. 若命题p∧q为假,且 为假,则( )
A. p或q为假 B. q假
C. q真 D. p假
5.函数在区间 上的最大值是( )
A.1 B.9 C. 27 D.
6.下列函数中,在上是减函数的是( )
A. B. C. D.
7.已知,则“”是“”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
8.方程的根所在的区间是( )
A. B. C. D.
9.函数的图像大致是( )
10.给出函数,则( )
A.10 B.12 C.8 D.14
11.若曲线在点处的切线方程是,则( )
A. B. C. D .
12、对于函数①,②,
判断如下两个命题的真假:
命题甲:在区间上是增函数;
命题乙:在区间上恰有两个零点,且。
能使命题甲、乙均为真的函数的序号是( )
A.①② B.② C.全不满足 D.①
第Ⅱ卷(非选择题 共90分)
若函数是奇函数,且,则 .
若命题“存在实数x,使”的否定是假命题,则实数a的取值范围为 。
若>3,则函数=在(0,2)内恰有________个零点.
若对任意有唯一确定的与之对应,则称为关于x,y的二元函数,现定义满足下列性质的为关于实数x,y的广义“距离”:
(1)非负性:,当且仅当x=y时取等号;
(2)对称性:
(3)三角形不等式:对任意的实数z均成立。
给出三个二元函数:①②
③
则所有能够成为关于x,y的广义“距离”的序号为 。
三、解答题:17-21每题满分12分,22题满分14分.解答须写文字说明、证明过程、演算步骤.
17.设命题:函数f(x)=x3-ax-1在区间上单调递减;命题:函数的值域是.如果命题为真命题,为假命题,求的取值范围.
集合A={x|x2-2x-3≤0,x∈R},B={x|x2-2mx+m2-4≤0,x∈R,m∈R}.
(1)若A∩B=[0,3],求实数m的值;
(2)若A ,求实数m的取值范围.
19、已知是上的奇函数,且当时,,
(1)当时,的解析式 ;
求函数的零点。
20. 2010年9月5日生效的一年期个人贷款利率为7.29%,小陈准备购一部汽车,购车一年后一次性付清车款,这时某商业银行推出一种一年期优惠贷款业务,年利率为,且(0.045,0.062),贷款量与利率的平方成正比,因此,小陈申请这种一年期优惠贷款.(利息=贷款量乘以利率)
写出小陈采用优惠贷款方式贷款应支付的利息;
(2) 一年期优惠利率为多少时,两种贷款的利息差最大
21.已知关于x的二次函数f(x)=x2+(2t-1)x+1-2t.
(1)求证:对于任意t∈R,方程f(x)=1必有实数根;
(2)若<t<,求证:方程f(x)=0在区间(-1,0)及(0,)内各有一个实数根.
22.设函数(),其中.
(Ⅰ)当时,求曲线在点处的切线方程;
(Ⅱ)当时,求函数的极大值和极小值;
(Ⅲ)当时,是否存在函数图像上两点以及函数图像上两点,使得以这四点为顶点的四边形ABCD满足如下条件:四边形ABCD是平行四边形;轴;。若存在,指出四边形ABCD的个数;若不存在,说明理由。
芗城中学10-11下学期高二年期末考试卷
数学(文科)试卷答案
选择题(每题5分)
解答题(12*5+14=74)
17、
...10分
综上所述:..........12分
(2) RB={x|x
A RB,∴m-2>3或m+2<-1................10分
∴m>5或m<-3..................12分
19、(本小题12分)
解:(1)当时,
则 .....2分
∵ 是的奇函数 ∴.......4分
∴当时,
……………6分
(本小题12分)
(1)由题意,贷款量为(,应支付利息=
(2)小陈的两种贷款方式的利息差为
令=0,解得或
当
所以,时,利息差取得极大值,即一年期优惠利率为4.68%时,利息差最大.
(2)当<t<时,因为f(-1)=3-4t=4(-t)>0,
f(0)=1-2t=2(-t)<0,f()=+(2t-1)+1-2t=-t>0,.........9分
f(-1)f(0)<0 , f(0)f()<0.........11分
所以方程f(x)=0在区间(-1,0)及(0,)内各有一个实数根.....12分
22.(Ⅰ)当时,,得,且,.所以,曲线在点处的切线方程是,整理得......4分
(Ⅱ)解:,.
令,解得或. .....6分
由于,以下分两种情况讨论.
(1)若,当变化时,的正负如下表:
因此,函数在处取得极小值,且;
函数在处取得极大值,且.
若,当变化时,的正负如下表:
因此,函数在处取得极小值,且;
函数在处取得极大值,且........10分
令,得或
由表格知,为的极大值,为的极大值,而 ,故的图像与x轴有且只有一个交点,有且只有一个零点。
时,,令,,
由知为的极大值,为的极大值,而
,故的图像与x轴有三个交点,有三个零点。
由知,方程有四个不同的实根,从小到大依次记为,这四个根对应的四条线段中的每两条对应一个平行四边形ABCD,共有6个,所以满足题意的平行四边形ABCD有6个。...........14分
同课章节目录
