人教七下数学5.3.1平行线的性质教案(2课时,表格式)
文档属性
| 名称 | 人教七下数学5.3.1平行线的性质教案(2课时,表格式) |  | |
| 格式 | docx | ||
| 文件大小 | 75.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-07 07:07:50 | ||
图片预览

文档简介
(总第八课时)5.3.1平行线的性质(第1课时)
年级
七年级
课题
5.3.1平行线的性质(1)
课型
新授
教
学
目
标
知识
技能
1.探索并掌握平行线的三条性质。.
2.能用平行线性质进行简单的推理和计算.
过程
方法
经历观察、操作、推理、交流等活动,进一步发展空间观念和推理能力毛.
情感
态度
培养探索精神,培养合作交流能力.
教学重点
探索并掌握平行线的性质,能用平行线性质进行简单的推理和计算.
教学难点
区分平行线的性质和判定.
教学方法
启发、讨论、探究
教学手段
多媒体
教
学
过
程
设
计
问题与情境
师生活动
情
景
引
入
1.回忆平行线的判定方法:
用文字和符号两种方法表示
2.如果两条直线平行,那么同位角、内错角、同旁内角有何数量关系?
学生猜想答案
由性质和判定的逻辑关系引入新课,培养学生直觉思维。
合
作
探
究
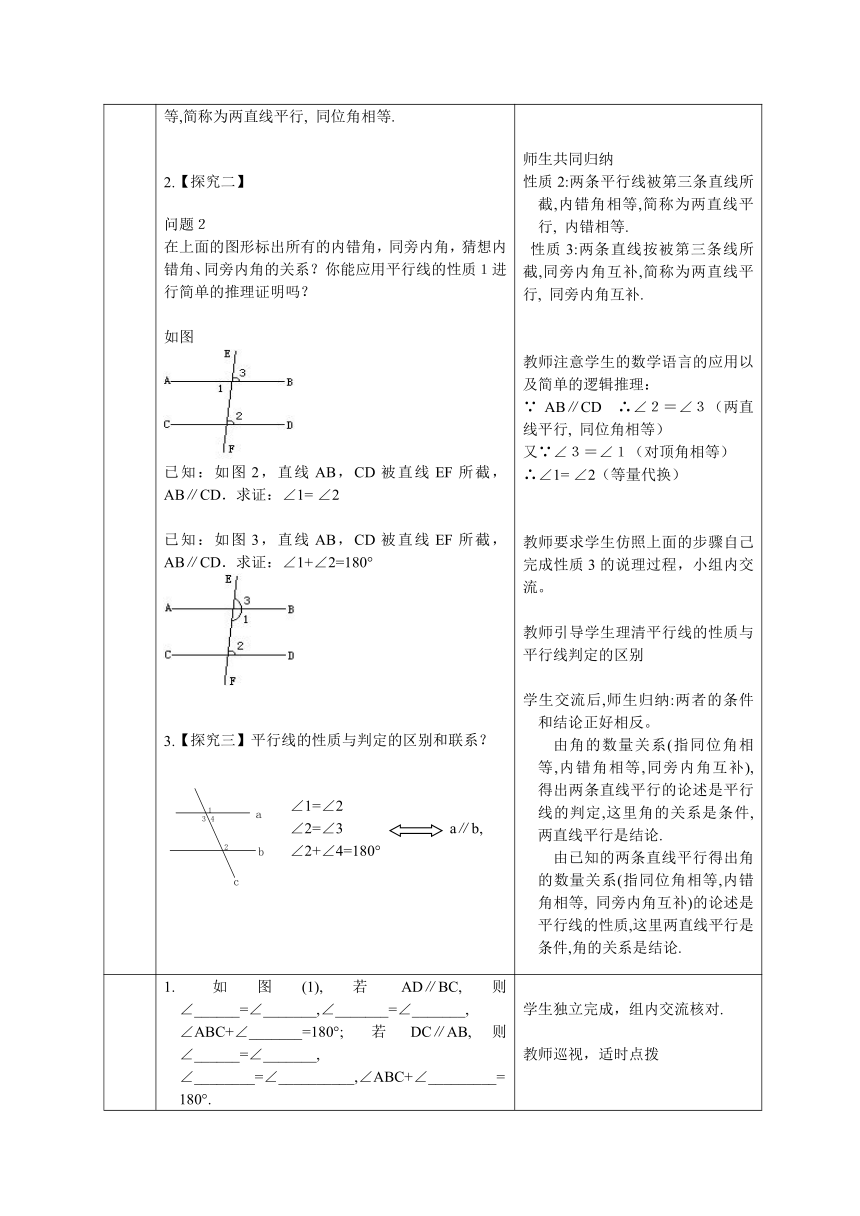
1.【探究一】
问题1:学生画出下图进行实验观察.设l1∥l2,l3与它们相交,请度量∠1和∠2的大小,
你能发现什么关系?请同学们再作出直线l4,再度量一下∠3和∠4的大小,你还能发现它们有什么关系?
师生归纳平行线的性质,教师板书.
性质1:两条平行线被第三条直线所截,同位角相等,简称为两直线平行,
同位角相等.
2.【探究二】
问题2
在上面的图形标出所有的内错角,同旁内角,猜想内错角、同旁内角的关系?你能应用平行线的性质1进行简单的推理证明吗?
如图
已知:如图2,直线AB,CD被直线EF所截,AB∥CD.求证:∠1=
∠2
已知:如图3,直线AB,CD被直线EF所截,AB∥CD.求证:∠1+∠2=180°
3.【探究三】平行线的性质与判定的区别和联系?
∠1=∠2
∠2=∠3
a∥b,
∠2+∠4=180°
学生合作实验.
发现并归纳平行线的性质1
师生共同归纳
性质2:两条平行线被第三条直线所截,内错角相等,简称为两直线平行,
内错相等.
性质3:两条直线按被第三条线所截,同旁内角互补,简称为两直线平行,
同旁内角互补.
教师注意学生的数学语言的应用以及简单的逻辑推理:
∵
AB∥CD ∴∠2=∠3(两直线平行,
同位角相等)
又∵∠3=∠1(对顶角相等)
∴∠1=
∠2(等量代换)
教师要求学生仿照上面的步骤自己完成性质3的说理过程,小组内交流。
教师引导学生理清平行线的性质与平行线判定的区别
学生交流后,师生归纳:两者的条件和结论正好相反。
由角的数量关系(指同位角相等,内错角相等,同旁内角互补),
得出两条直线平行的论述是平行线的判定,这里角的关系是条件,两直线平行是结论.
由已知的两条直线平行得出角的数量关系(指同位角相等,内错角相等,
同旁内角互补)的论述是平行线的性质,这里两直线平行是条件,角的关系是结论.
巩
固
应
用
1.
如图(1),若AD∥BC,则∠______=∠_______,∠_______=∠_______,
∠ABC+∠_______=180°;
若DC∥AB,则∠______=∠_______,
∠________=∠__________,∠ABC+∠_________=180°.
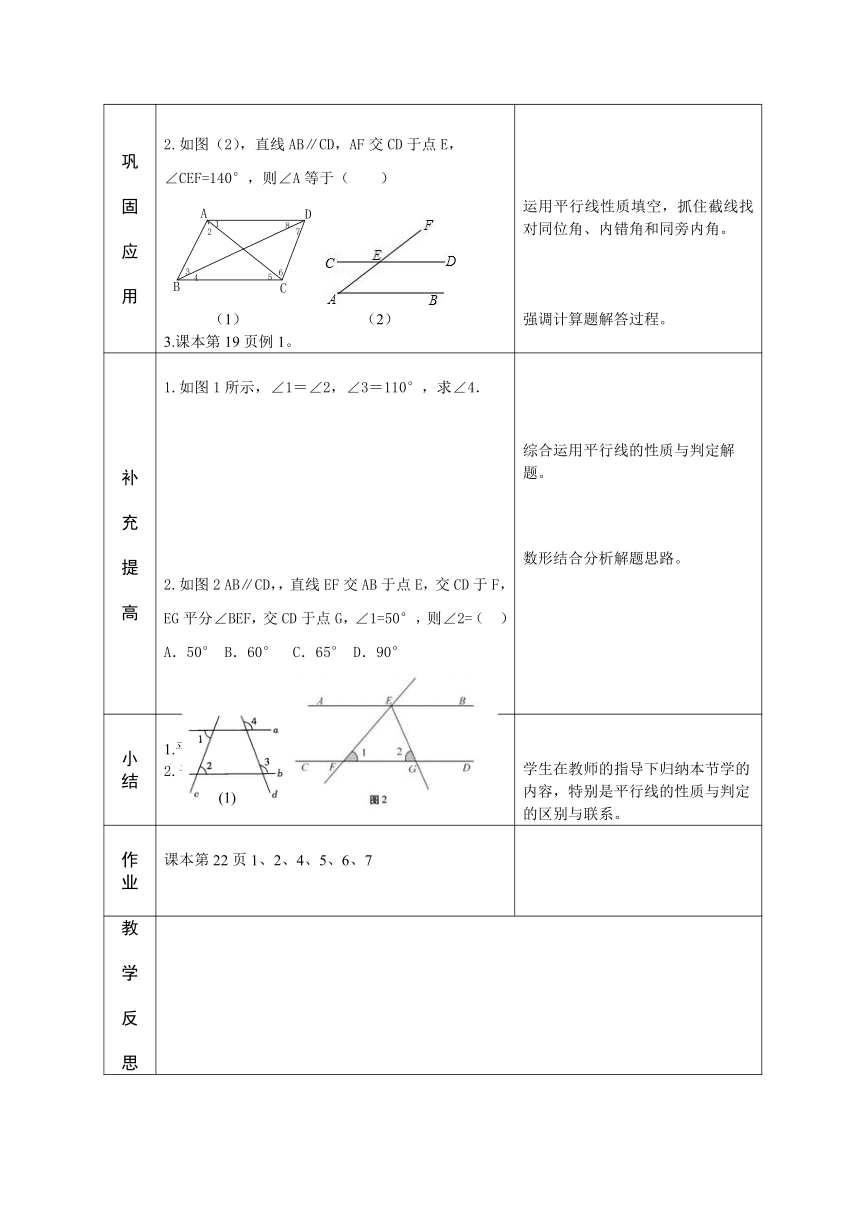
2.如图(2),直线AB∥CD,AF交CD于点E,∠CEF=140°,则∠A等于( )
(1)
(2)
3.课本第19页例1。
学生独立完成,组内交流核对.
教师巡视,适时点拨
运用平行线性质填空,抓住截线找对同位角、内错角和同旁内角。
强调计算题解答过程。
补
充
提
高
1.如图1所示,∠1=∠2,∠3=110°,求∠4.
2.如图2
AB∥CD,,直线EF交AB于点E,交CD于F,EG平分∠BEF,交CD于点G,∠1=50°,则∠2=(
)
A.50°
B.60°
C.65°
D.90°
综合运用平行线的性质与判定解题。
数形结合分析解题思路。
小
结
1.平行线的性质。
2.平行线性质与判定的区别与联系。
学生在教师的指导下归纳本节学的
内容,特别是平行线的性质与判定
的区别与联系。
作
业
课本第22页1、2、4、5、6、7
教
学
反
思
(总第九课时)5.3.1平行线的性质(第2课时)
年级
七年级
课题
5.3.1平行线的性质(2)
课型
新授
教
学
目
标
知识
技能
1.熟练掌握平行线的判定和性质。.
2.能综合运用平行线性质和判定进行推理和计算.
过程
方法
培养学生“两头凑”分析方法,提高学生推理能力,领会化归思想毛.
情感
态度
感受数学活动充满探索性与创造性,激发学生的探究热情.
教学重点
综合运用平行线性质和判定进行推理和计算.
教学难点
通过添加辅助线利用平行线知识解题.
教学方法
启发、讨论、探究
教学手段
多媒体
教
学
过
程
设
计
问题与情境
师生活动
复
习
引
入
1.回忆平行线的判定方法:
平行公理推论,三条判定定理
2.回忆平行线的性质:
复习平行线的性质和判定,为解题奠定基础。
合
作
探
究
1.例1:如图,AB∥CD,∠1=102°,求∠2、∠3、∠4、∠5的度数,并说明根据?
2.例2:如图,EF过△ABC的一个顶点A,且EF∥BC,如果∠B=40°,∠2=75°,那么∠1、∠3、∠C、∠BAC+∠B+∠C各是多少度,为什么?
3.
如图,已知B、E分别是AC、DF上的点,∠1=∠2∠C=∠D.∠A与∠F相等吗?请说明理由.
4.
如图,已知AB∥EF,猜想∠B、∠F、∠C之间的关系,写出这种关系,试加以说明.
作CD∥AB,因为AB∥EF,CD∥AB,所以CD∥EF(平行于同一条直线的两条直线互相平行).
所以∠F=∠FCD(两直线平行,内错角相等).因为CD∥AB.
所以∠B=∠BCD(两直线平行,内错角相等).
所以∠B+∠F=∠BCF.
改变点C的位置进行探究。
运用平行线性质计算,学生独立思考完成。
引导学生用“两头凑”方法分析思路
教师分析思路过程,学生练习写推理过程。
猜想:∠B+∠F=∠C.
∠B与∠C是直线AB、CF被直线BC所截而成的内错角,但是AB与CF不平行.能不能创造条件,应用平行线性质,学生自然想到过点C作CD∥AB,这样就能用上平行线的性质,得到∠B=∠BCD.
接下来需证∠F=∠FCD,只要说明CD与EF平行,你能做到这一点吗?
小组合作,激发学生探究精神。
巩
固
应
用
1.设a、b、c为同一平面内的三条直线,下列判断不正确的是(
)
A.设a⊥c,b⊥c,则a⊥b
B.若a∥c,b∥c,则a∥b
C.若a∥b,b⊥c,则a⊥c
D.若a⊥b,b⊥c,则a⊥c
2.两条直线被第三条直线所截,则一组内错角的平分线的位置关系是(
)
A.平行;
B.垂直;
C.相交但不垂直;D.平行或相交
变式:把“内错角”变为“同位角”、“同旁内角”
3.一大门的栏杆如图所示,垂直于地面于,平行于地面,则∠ABC+∠BCD
=
度.
学生综合运用平行线性质和判定说理,培养学生探究意识。
运用平行线知识解决实际问题,激发学生学习兴趣。
补
充
提
高
已知:如图,∠AGD=∠ACB,
∠1=∠2,CD与EF平行吗?为什么?
学生综合运用平行线性质和判定说理,激发钻研精神。
教师启发,学生合作完成。
小
结
1.综合运用平行线的性质与判定计算和说理。
2.掌握“两头凑”分析方法,感悟化归思想。
反思本节课所学知识、方法和思想。
作
业
课本第24页8、13、15题
教
学
反
思
年级
七年级
课题
5.3.1平行线的性质(1)
课型
新授
教
学
目
标
知识
技能
1.探索并掌握平行线的三条性质。.
2.能用平行线性质进行简单的推理和计算.
过程
方法
经历观察、操作、推理、交流等活动,进一步发展空间观念和推理能力毛.
情感
态度
培养探索精神,培养合作交流能力.
教学重点
探索并掌握平行线的性质,能用平行线性质进行简单的推理和计算.
教学难点
区分平行线的性质和判定.
教学方法
启发、讨论、探究
教学手段
多媒体
教
学
过
程
设
计
问题与情境
师生活动
情
景
引
入
1.回忆平行线的判定方法:
用文字和符号两种方法表示
2.如果两条直线平行,那么同位角、内错角、同旁内角有何数量关系?
学生猜想答案
由性质和判定的逻辑关系引入新课,培养学生直觉思维。
合
作
探
究
1.【探究一】
问题1:学生画出下图进行实验观察.设l1∥l2,l3与它们相交,请度量∠1和∠2的大小,
你能发现什么关系?请同学们再作出直线l4,再度量一下∠3和∠4的大小,你还能发现它们有什么关系?
师生归纳平行线的性质,教师板书.
性质1:两条平行线被第三条直线所截,同位角相等,简称为两直线平行,
同位角相等.
2.【探究二】
问题2
在上面的图形标出所有的内错角,同旁内角,猜想内错角、同旁内角的关系?你能应用平行线的性质1进行简单的推理证明吗?
如图
已知:如图2,直线AB,CD被直线EF所截,AB∥CD.求证:∠1=
∠2
已知:如图3,直线AB,CD被直线EF所截,AB∥CD.求证:∠1+∠2=180°
3.【探究三】平行线的性质与判定的区别和联系?
∠1=∠2
∠2=∠3
a∥b,
∠2+∠4=180°
学生合作实验.
发现并归纳平行线的性质1
师生共同归纳
性质2:两条平行线被第三条直线所截,内错角相等,简称为两直线平行,
内错相等.
性质3:两条直线按被第三条线所截,同旁内角互补,简称为两直线平行,
同旁内角互补.
教师注意学生的数学语言的应用以及简单的逻辑推理:
∵
AB∥CD ∴∠2=∠3(两直线平行,
同位角相等)
又∵∠3=∠1(对顶角相等)
∴∠1=
∠2(等量代换)
教师要求学生仿照上面的步骤自己完成性质3的说理过程,小组内交流。
教师引导学生理清平行线的性质与平行线判定的区别
学生交流后,师生归纳:两者的条件和结论正好相反。
由角的数量关系(指同位角相等,内错角相等,同旁内角互补),
得出两条直线平行的论述是平行线的判定,这里角的关系是条件,两直线平行是结论.
由已知的两条直线平行得出角的数量关系(指同位角相等,内错角相等,
同旁内角互补)的论述是平行线的性质,这里两直线平行是条件,角的关系是结论.
巩
固
应
用
1.
如图(1),若AD∥BC,则∠______=∠_______,∠_______=∠_______,
∠ABC+∠_______=180°;
若DC∥AB,则∠______=∠_______,
∠________=∠__________,∠ABC+∠_________=180°.
2.如图(2),直线AB∥CD,AF交CD于点E,∠CEF=140°,则∠A等于( )
(1)
(2)
3.课本第19页例1。
学生独立完成,组内交流核对.
教师巡视,适时点拨
运用平行线性质填空,抓住截线找对同位角、内错角和同旁内角。
强调计算题解答过程。
补
充
提
高
1.如图1所示,∠1=∠2,∠3=110°,求∠4.
2.如图2
AB∥CD,,直线EF交AB于点E,交CD于F,EG平分∠BEF,交CD于点G,∠1=50°,则∠2=(
)
A.50°
B.60°
C.65°
D.90°
综合运用平行线的性质与判定解题。
数形结合分析解题思路。
小
结
1.平行线的性质。
2.平行线性质与判定的区别与联系。
学生在教师的指导下归纳本节学的
内容,特别是平行线的性质与判定
的区别与联系。
作
业
课本第22页1、2、4、5、6、7
教
学
反
思
(总第九课时)5.3.1平行线的性质(第2课时)
年级
七年级
课题
5.3.1平行线的性质(2)
课型
新授
教
学
目
标
知识
技能
1.熟练掌握平行线的判定和性质。.
2.能综合运用平行线性质和判定进行推理和计算.
过程
方法
培养学生“两头凑”分析方法,提高学生推理能力,领会化归思想毛.
情感
态度
感受数学活动充满探索性与创造性,激发学生的探究热情.
教学重点
综合运用平行线性质和判定进行推理和计算.
教学难点
通过添加辅助线利用平行线知识解题.
教学方法
启发、讨论、探究
教学手段
多媒体
教
学
过
程
设
计
问题与情境
师生活动
复
习
引
入
1.回忆平行线的判定方法:
平行公理推论,三条判定定理
2.回忆平行线的性质:
复习平行线的性质和判定,为解题奠定基础。
合
作
探
究
1.例1:如图,AB∥CD,∠1=102°,求∠2、∠3、∠4、∠5的度数,并说明根据?
2.例2:如图,EF过△ABC的一个顶点A,且EF∥BC,如果∠B=40°,∠2=75°,那么∠1、∠3、∠C、∠BAC+∠B+∠C各是多少度,为什么?
3.
如图,已知B、E分别是AC、DF上的点,∠1=∠2∠C=∠D.∠A与∠F相等吗?请说明理由.
4.
如图,已知AB∥EF,猜想∠B、∠F、∠C之间的关系,写出这种关系,试加以说明.
作CD∥AB,因为AB∥EF,CD∥AB,所以CD∥EF(平行于同一条直线的两条直线互相平行).
所以∠F=∠FCD(两直线平行,内错角相等).因为CD∥AB.
所以∠B=∠BCD(两直线平行,内错角相等).
所以∠B+∠F=∠BCF.
改变点C的位置进行探究。
运用平行线性质计算,学生独立思考完成。
引导学生用“两头凑”方法分析思路
教师分析思路过程,学生练习写推理过程。
猜想:∠B+∠F=∠C.
∠B与∠C是直线AB、CF被直线BC所截而成的内错角,但是AB与CF不平行.能不能创造条件,应用平行线性质,学生自然想到过点C作CD∥AB,这样就能用上平行线的性质,得到∠B=∠BCD.
接下来需证∠F=∠FCD,只要说明CD与EF平行,你能做到这一点吗?
小组合作,激发学生探究精神。
巩
固
应
用
1.设a、b、c为同一平面内的三条直线,下列判断不正确的是(
)
A.设a⊥c,b⊥c,则a⊥b
B.若a∥c,b∥c,则a∥b
C.若a∥b,b⊥c,则a⊥c
D.若a⊥b,b⊥c,则a⊥c
2.两条直线被第三条直线所截,则一组内错角的平分线的位置关系是(
)
A.平行;
B.垂直;
C.相交但不垂直;D.平行或相交
变式:把“内错角”变为“同位角”、“同旁内角”
3.一大门的栏杆如图所示,垂直于地面于,平行于地面,则∠ABC+∠BCD
=
度.
学生综合运用平行线性质和判定说理,培养学生探究意识。
运用平行线知识解决实际问题,激发学生学习兴趣。
补
充
提
高
已知:如图,∠AGD=∠ACB,
∠1=∠2,CD与EF平行吗?为什么?
学生综合运用平行线性质和判定说理,激发钻研精神。
教师启发,学生合作完成。
小
结
1.综合运用平行线的性质与判定计算和说理。
2.掌握“两头凑”分析方法,感悟化归思想。
反思本节课所学知识、方法和思想。
作
业
课本第24页8、13、15题
教
学
反
思
