1.3.1.1 有理数的加法 课件(共27张PPT)
文档属性
| 名称 | 1.3.1.1 有理数的加法 课件(共27张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-07 20:40:23 | ||
图片预览







文档简介
(共27张PPT)
1.3
有理数的加减法
1.3.1
有理数的加法
第1课时
有理数的加法
人教版·七年级上册
上课课件
1.了解有理数加法的意义,理解有理数加法法则的合理性.
2.能运用该法则准确进行有理数的加法运算.(重点)
3.经历探索有理数加法法则的过程,理解并掌握有理数加法的法则.(难点)
学习目标
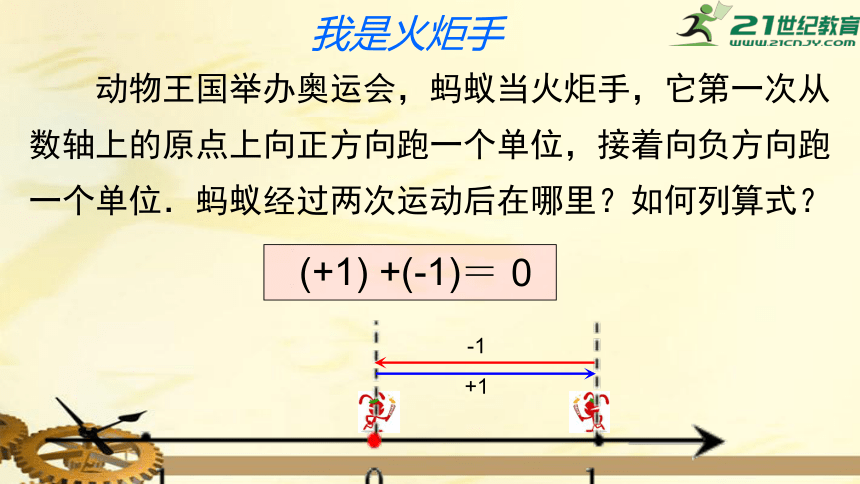
我是火炬手
+1
-1
(+1)
+(-1)=
0
动物王国举办奥运会,蚂蚁当火炬手,它第一次从数轴上的原点上向正方向跑一个单位,接着向负方向跑一个单位.蚂蚁经过两次运动后在哪里?如何列算式?
在小学,我们学过正数及0的加法运算.引入负数后,怎样进行加法运算呢?
实际问题中,有时也会遇到与负数有关的加法运算.例如,在本章引言中,把收入记作正数,支出记作负数,在求“结余”时,需要计算8.5+(-4.5),4.0+(-5.2)等.
新课导入
小学学过的加法类型是正数与正数相加、正数与0相加.引入负数后,加法的类型还有哪几种呢?
推进新课
思考
正数
0
负数
正数
0
负数
正数+正数
0+正数
负数+正数
0+0
负数+0
0+负数
负数+负数
正数+0
正数+负数
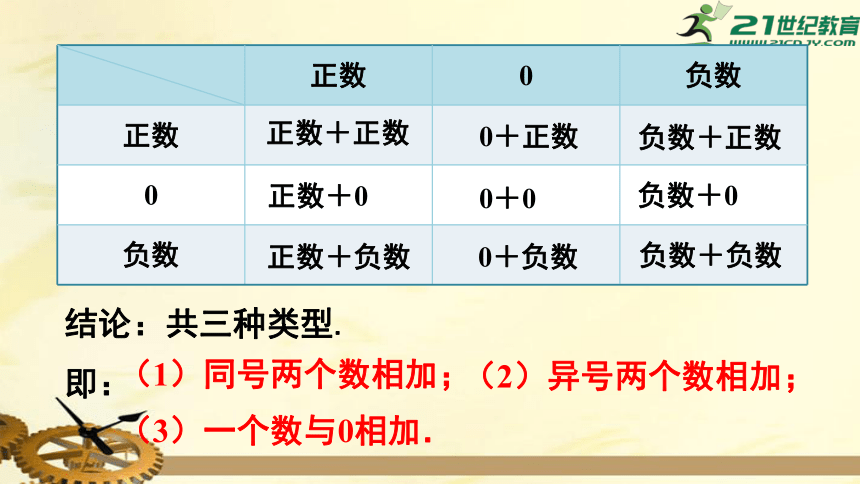
结论:共三种类型.
即:
(1)同号两个数相加;
(2)异号两个数相加;
(3)一个数与0相加.
探究有理数加法的法则
知识点1
一个物体作左右方向的运动,我们规定向左为负,向右为正.比如:向右运动5
m记作5
m,向左运动5
m记作-5
m.
观察探究
(1)如果物体先向右运动5
m,再向右运动了3
m,那么两次运动的最后结果是什么?可以用怎样的算式表示?
(+5)+(+3)
=
8
-1
0
1
2
3
4
5
6
7
8
5
3
+
8
思考
(2)如果物体先向左运动5
m,再向左运动3
m,那么两次运动的最后结果是什么?可以用怎样的算式表示?
-3
-5
(-5)+(-3)=-8
+
-8
-8
-7
-6
-5
-4
-3
-2
-1
0
1
根据以上两个算式能否尝试总结同号两数相加的法则?
(+5)+(+3)=
8
(-5)+(-3)=-8
归纳法则
注意关注加数的符号和绝对值
同号两数相加,取相同符号,并把绝对值相加.
结论:
利用数轴,求以下物体两次运动的结果,并用算式表示:
(1)先向左运动3
m,再向右运动5
m,
物体从起点向____运动了____m,____________;
(2)先向右运动了3
m,再向左运动了5
m,
物体从起点向____运动了____m,____________;
(3)先向左运动了5
m,再向右运动了5
m,
物体从起点运动了____m,_____________.
0
右
左
2
2
(-3)+5=2
3+(-5)=-2
(-5)+5=
0
探究
根据以上三个算式能否尝试总结异号两数相加的法则?
注意关注加数的符号和绝对值
绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值,互为相反数的两个数相加得0
.
结论:
(-3)+5=
2
3+(-5)=-2
(-5)+5=
0
归纳法则
如果物体第1
s向右(或左)运动5
m,第2
s原地不动,那么2
s后物体从起点向右(或左)运动了5
m.如何用算式表示呢?
直接说出结论
5+0=5.
或
(-5)+0=-5.
结论:
一个数同0相加,仍得这个数.
归纳法则
1.同号两数相加,取相同的符号,并把绝对值相加.
2.绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值.互为相反数的两个数相加得0.
3.一个数同0相加,仍得这个数.
有理数加法法则:
例
计算:
(1)(-3)+(-9);
(2)(-4.7)+3.9;
(3)
0+(-7);
(4)(-9)+(+9).
有理数加法的运算
知识点2
解:
(1)(-3)+(-9)=
同号两数相加
-
(3+9)
=-12;
(2)(-4.7)+3.9=
取相同符号
把绝对值相加
(4.7-3.9)
-
=-0.8;
异号两数相加
取绝对值较大加数的符号
用较大的绝对值减较小的绝对值
解:
(3)
0+(-7)=-7;
(4)(-9)+(+9)=
0.
有理数加法的运算步骤:
一要辨别加数的类型(同号、异号);
二要确定和的符号;
三要计算绝对值的和(或差).
可要记住哟!
即“一看、二定、三算”.
教科书
第18页
练习
课堂练习
1.用算式表示下面的结果:
(1)温度由-4
℃上升7
℃;
(2)收入7元,又支出5元.
-4+7=3
7-5=2
2.口算:
(1)(-4)+(-6);
(2)
4+(-6);
(3)(-4)+6;
(4)(-4)+4;
(5)(-4)+14;
(6)(-14)+4;
(7)
6+(-6);
(8)
0+(-6).
-10
-2
2
0
10
-10
0
-6
随堂演练
1.两个有理数的和为负数,则这两个数一定(
).
A.都是负数
B.只有一个负数
C.至少有一个负数
D.无法确定
C
基础巩固
2.请你用生活中的例子解释算式(+3)+(-3)
=
0;(-1)+(-2)
=
-3.
综合应用
解:①冬季某天早晨温度为0度,到中午气温上升了3度,再到下午又下降了3度,下午气温为0度;
②取向东为正方向,先向西走了1
km,后又走了2
km,一共向西走了3
km.
3.数a,b表示的点如图所示,则
(1)a
+
b
_____
0;
(2)a
+
(-b)_____
0;
(3)(-a)
+
b
_____
0;
(4)(-a)
+
(-b)
_____0.
(填“>”“<”或“=”)
拓展延伸
>
<
>
<
课堂小结
1.同号两数相加,取相同的符号,并把绝对值相加.
2.绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值,互为相反数的两个数相加得0.
3.一个数同0相加,仍得这个数.
有理数加法法则:
课后作业
1、完成教材本课时对应习题;
2、完成同步练习册本课时的习题。
谢谢观看
THANKS
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!!
1.3
有理数的加减法
1.3.1
有理数的加法
第1课时
有理数的加法
人教版·七年级上册
上课课件
1.了解有理数加法的意义,理解有理数加法法则的合理性.
2.能运用该法则准确进行有理数的加法运算.(重点)
3.经历探索有理数加法法则的过程,理解并掌握有理数加法的法则.(难点)
学习目标
我是火炬手
+1
-1
(+1)
+(-1)=
0
动物王国举办奥运会,蚂蚁当火炬手,它第一次从数轴上的原点上向正方向跑一个单位,接着向负方向跑一个单位.蚂蚁经过两次运动后在哪里?如何列算式?
在小学,我们学过正数及0的加法运算.引入负数后,怎样进行加法运算呢?
实际问题中,有时也会遇到与负数有关的加法运算.例如,在本章引言中,把收入记作正数,支出记作负数,在求“结余”时,需要计算8.5+(-4.5),4.0+(-5.2)等.
新课导入
小学学过的加法类型是正数与正数相加、正数与0相加.引入负数后,加法的类型还有哪几种呢?
推进新课
思考
正数
0
负数
正数
0
负数
正数+正数
0+正数
负数+正数
0+0
负数+0
0+负数
负数+负数
正数+0
正数+负数
结论:共三种类型.
即:
(1)同号两个数相加;
(2)异号两个数相加;
(3)一个数与0相加.
探究有理数加法的法则
知识点1
一个物体作左右方向的运动,我们规定向左为负,向右为正.比如:向右运动5
m记作5
m,向左运动5
m记作-5
m.
观察探究
(1)如果物体先向右运动5
m,再向右运动了3
m,那么两次运动的最后结果是什么?可以用怎样的算式表示?
(+5)+(+3)
=
8
-1
0
1
2
3
4
5
6
7
8
5
3
+
8
思考
(2)如果物体先向左运动5
m,再向左运动3
m,那么两次运动的最后结果是什么?可以用怎样的算式表示?
-3
-5
(-5)+(-3)=-8
+
-8
-8
-7
-6
-5
-4
-3
-2
-1
0
1
根据以上两个算式能否尝试总结同号两数相加的法则?
(+5)+(+3)=
8
(-5)+(-3)=-8
归纳法则
注意关注加数的符号和绝对值
同号两数相加,取相同符号,并把绝对值相加.
结论:
利用数轴,求以下物体两次运动的结果,并用算式表示:
(1)先向左运动3
m,再向右运动5
m,
物体从起点向____运动了____m,____________;
(2)先向右运动了3
m,再向左运动了5
m,
物体从起点向____运动了____m,____________;
(3)先向左运动了5
m,再向右运动了5
m,
物体从起点运动了____m,_____________.
0
右
左
2
2
(-3)+5=2
3+(-5)=-2
(-5)+5=
0
探究
根据以上三个算式能否尝试总结异号两数相加的法则?
注意关注加数的符号和绝对值
绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值,互为相反数的两个数相加得0
.
结论:
(-3)+5=
2
3+(-5)=-2
(-5)+5=
0
归纳法则
如果物体第1
s向右(或左)运动5
m,第2
s原地不动,那么2
s后物体从起点向右(或左)运动了5
m.如何用算式表示呢?
直接说出结论
5+0=5.
或
(-5)+0=-5.
结论:
一个数同0相加,仍得这个数.
归纳法则
1.同号两数相加,取相同的符号,并把绝对值相加.
2.绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值.互为相反数的两个数相加得0.
3.一个数同0相加,仍得这个数.
有理数加法法则:
例
计算:
(1)(-3)+(-9);
(2)(-4.7)+3.9;
(3)
0+(-7);
(4)(-9)+(+9).
有理数加法的运算
知识点2
解:
(1)(-3)+(-9)=
同号两数相加
-
(3+9)
=-12;
(2)(-4.7)+3.9=
取相同符号
把绝对值相加
(4.7-3.9)
-
=-0.8;
异号两数相加
取绝对值较大加数的符号
用较大的绝对值减较小的绝对值
解:
(3)
0+(-7)=-7;
(4)(-9)+(+9)=
0.
有理数加法的运算步骤:
一要辨别加数的类型(同号、异号);
二要确定和的符号;
三要计算绝对值的和(或差).
可要记住哟!
即“一看、二定、三算”.
教科书
第18页
练习
课堂练习
1.用算式表示下面的结果:
(1)温度由-4
℃上升7
℃;
(2)收入7元,又支出5元.
-4+7=3
7-5=2
2.口算:
(1)(-4)+(-6);
(2)
4+(-6);
(3)(-4)+6;
(4)(-4)+4;
(5)(-4)+14;
(6)(-14)+4;
(7)
6+(-6);
(8)
0+(-6).
-10
-2
2
0
10
-10
0
-6
随堂演练
1.两个有理数的和为负数,则这两个数一定(
).
A.都是负数
B.只有一个负数
C.至少有一个负数
D.无法确定
C
基础巩固
2.请你用生活中的例子解释算式(+3)+(-3)
=
0;(-1)+(-2)
=
-3.
综合应用
解:①冬季某天早晨温度为0度,到中午气温上升了3度,再到下午又下降了3度,下午气温为0度;
②取向东为正方向,先向西走了1
km,后又走了2
km,一共向西走了3
km.
3.数a,b表示的点如图所示,则
(1)a
+
b
_____
0;
(2)a
+
(-b)_____
0;
(3)(-a)
+
b
_____
0;
(4)(-a)
+
(-b)
_____0.
(填“>”“<”或“=”)
拓展延伸
>
<
>
<
课堂小结
1.同号两数相加,取相同的符号,并把绝对值相加.
2.绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值,互为相反数的两个数相加得0.
3.一个数同0相加,仍得这个数.
有理数加法法则:
课后作业
1、完成教材本课时对应习题;
2、完成同步练习册本课时的习题。
谢谢观看
THANKS
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!!
