3.2 立体几何中的向量方法 课件-2021-2022学年高二上学期数学人教A版选修2-1(共20张PPT)
文档属性
| 名称 | 3.2 立体几何中的向量方法 课件-2021-2022学年高二上学期数学人教A版选修2-1(共20张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-08 09:49:50 | ||
图片预览





文档简介
(共20张PPT)
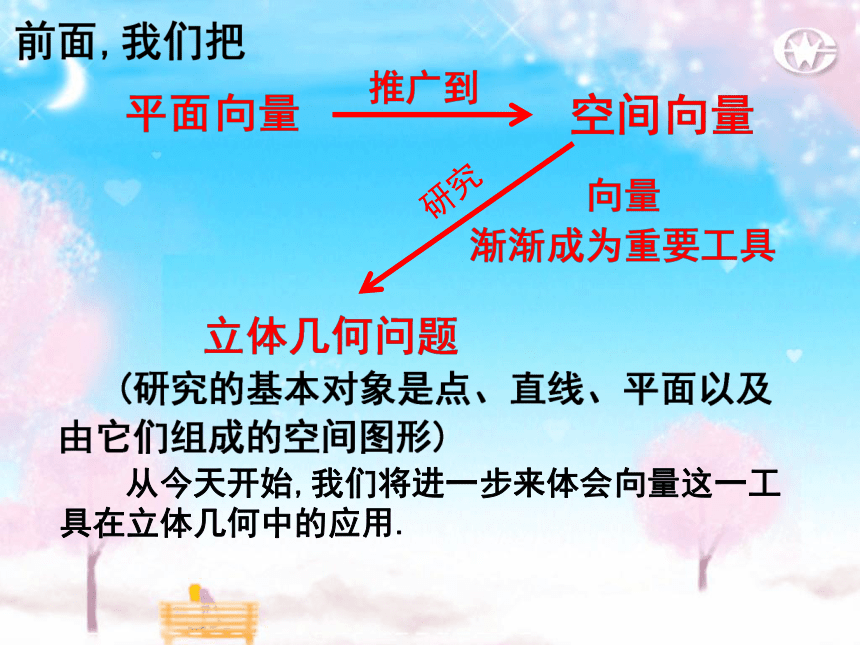
立体几何中的向量方法
研究
从今天开始,我们将进一步来体会向量这一工具在立体几何中的应用.
O
P
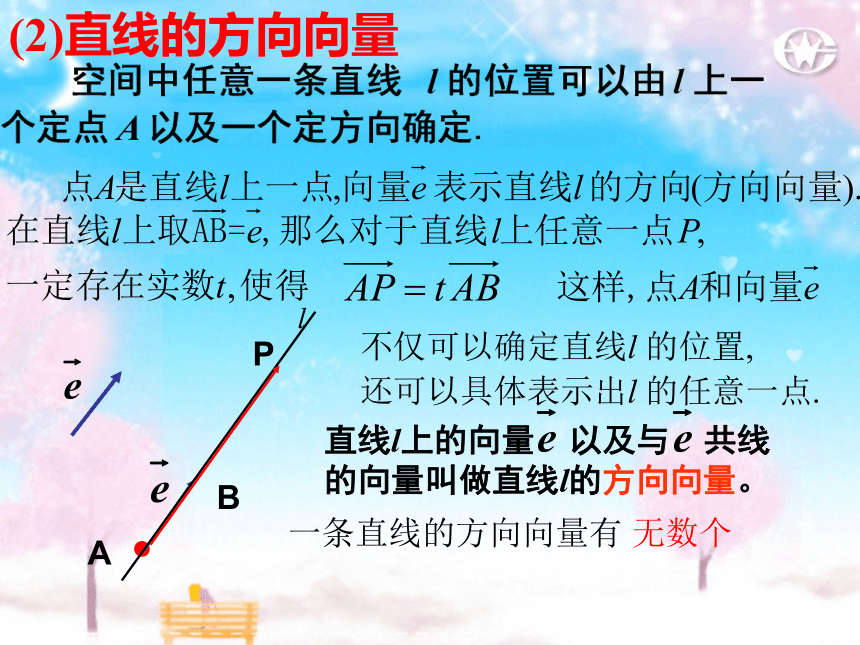
(2)直线的方向向量
A
B
直线l上的向量
以及与
共线的向量叫做直线l的方向向量。
P
一条直线的方向向量有
无数个
不仅可以确定直线l
的位置,
还可以具体表示出l
的任意一点.
P
O
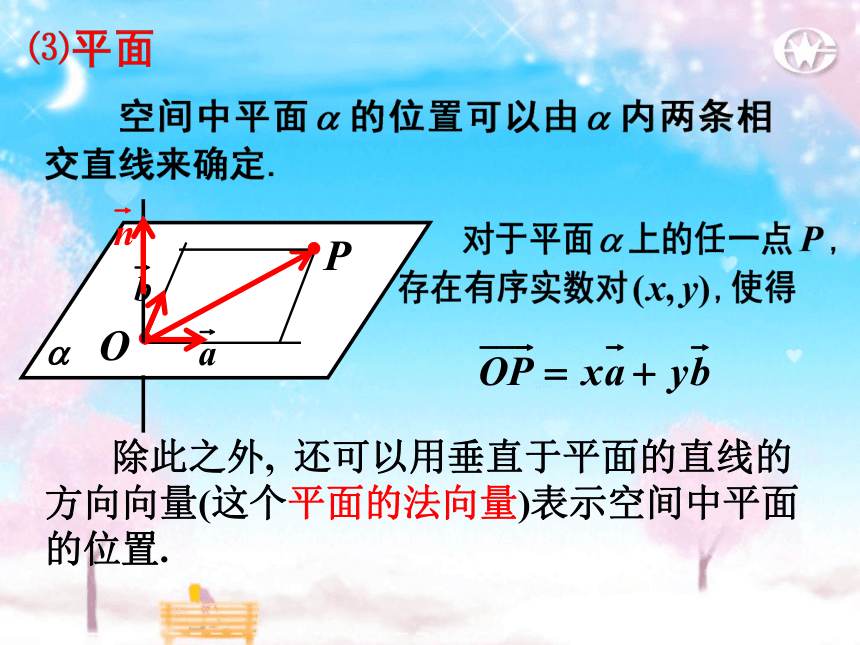
除此之外,
还可以用垂直于平面的直线的
方向向量(这个平面的法向量)表示空间中平面的位置.
由于垂直于同一平面的直线是互相平行的,
所以,可以用垂直于平面的直线的方向向量来刻画平面的“方向”。
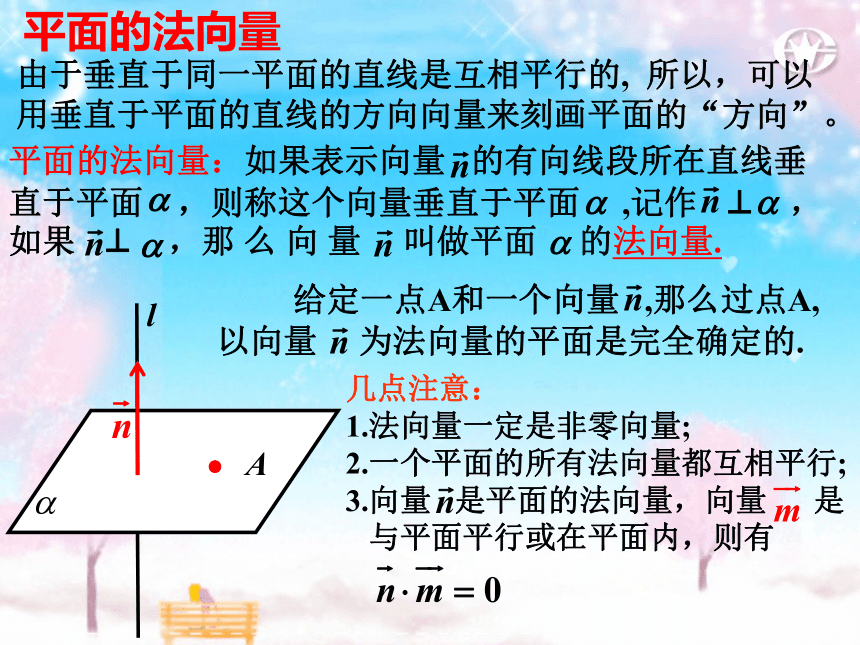
平面的法向量
平面的法向量:如果表示向量
的有向线段所在直线垂直于平面
,则称这个向量垂直于平面
,记作
⊥
,如果
⊥
,那
么
向
量
叫做平面
的法向量.
A
l
给定一点A和一个向量
,那么过点A,以向量
为法向量的平面是完全确定的.
几点注意:
1.法向量一定是非零向量;
2.一个平面的所有法向量都互相平行;
3.向量
是平面的法向量,向量
是
与平面平行或在平面内,则有
因为方向向量与法向量可以确定直线和平面的位置,所以我们可以利用直线的方向向量与平面的法向量表示空间直线、平面间的平行、垂直、夹角等位置关系。
1.设
分别是直线l1,l2的方向向量,根据下
列条件,判断l1,l2的位置关系.
题型一 利用方向向量和法向量判定线、面位置关系
[思路探索]
可先判断两直线的方向向量之间的位置关系,再转化为两直线间的位置关系.
2、设
分别是平面
的法向量,根据
下列条件判断平面
的位置关系.
[思路探索]
可先判断两平面的法向量之间的位置关系,再转化为两平面间的位置关系.
3、设
是平面
的法向量,
是直线l
的方向向
量,根据下列条件判断平面
与直线l
的位置关系.
[思路探索]
可先判断直线的方向向与平面的法向量
之间的位置关系,再转化为直线与平面间的位置关系.
题型二 求平面的法向量
(答案不唯一)
(设坐标,选向量,解方程,定结论)
1.在三棱锥S-ABC中,CS,CA,CB两两垂直,CA=CB=3,CS=2,在如图所示的坐标系中,
求平面SAB的一个法向量。
1.在三棱锥S-ABC中,CS,CA,CB两两垂直,CA=CB=3,CS=2,在如图所示的坐标系中,
求平面SAB的一个法向量。
谢谢合作!
下课了!
立体几何中的向量方法
研究
从今天开始,我们将进一步来体会向量这一工具在立体几何中的应用.
O
P
(2)直线的方向向量
A
B
直线l上的向量
以及与
共线的向量叫做直线l的方向向量。
P
一条直线的方向向量有
无数个
不仅可以确定直线l
的位置,
还可以具体表示出l
的任意一点.
P
O
除此之外,
还可以用垂直于平面的直线的
方向向量(这个平面的法向量)表示空间中平面的位置.
由于垂直于同一平面的直线是互相平行的,
所以,可以用垂直于平面的直线的方向向量来刻画平面的“方向”。
平面的法向量
平面的法向量:如果表示向量
的有向线段所在直线垂直于平面
,则称这个向量垂直于平面
,记作
⊥
,如果
⊥
,那
么
向
量
叫做平面
的法向量.
A
l
给定一点A和一个向量
,那么过点A,以向量
为法向量的平面是完全确定的.
几点注意:
1.法向量一定是非零向量;
2.一个平面的所有法向量都互相平行;
3.向量
是平面的法向量,向量
是
与平面平行或在平面内,则有
因为方向向量与法向量可以确定直线和平面的位置,所以我们可以利用直线的方向向量与平面的法向量表示空间直线、平面间的平行、垂直、夹角等位置关系。
1.设
分别是直线l1,l2的方向向量,根据下
列条件,判断l1,l2的位置关系.
题型一 利用方向向量和法向量判定线、面位置关系
[思路探索]
可先判断两直线的方向向量之间的位置关系,再转化为两直线间的位置关系.
2、设
分别是平面
的法向量,根据
下列条件判断平面
的位置关系.
[思路探索]
可先判断两平面的法向量之间的位置关系,再转化为两平面间的位置关系.
3、设
是平面
的法向量,
是直线l
的方向向
量,根据下列条件判断平面
与直线l
的位置关系.
[思路探索]
可先判断直线的方向向与平面的法向量
之间的位置关系,再转化为直线与平面间的位置关系.
题型二 求平面的法向量
(答案不唯一)
(设坐标,选向量,解方程,定结论)
1.在三棱锥S-ABC中,CS,CA,CB两两垂直,CA=CB=3,CS=2,在如图所示的坐标系中,
求平面SAB的一个法向量。
1.在三棱锥S-ABC中,CS,CA,CB两两垂直,CA=CB=3,CS=2,在如图所示的坐标系中,
求平面SAB的一个法向量。
谢谢合作!
下课了!
