第十章概率全章基础巩固试卷-2020-2021学年高一下学期数学人教A版(2019)必修第二册(Word含答案解析)
文档属性
| 名称 | 第十章概率全章基础巩固试卷-2020-2021学年高一下学期数学人教A版(2019)必修第二册(Word含答案解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-08 21:27:56 | ||
图片预览




文档简介
高一第二学期数学第十章概率全章基础巩固试卷-2020-2021学年人教版必修第二册
一、单选题
1.打靶次,事件表示“击中发”,其中、、、.那么表示(
)
A.全部击中
B.至少击中发
C.至少击中发
D.以上均不正确
2.下列试验是古典概型的是(
)
A.口袋中有2个白球和3个黑球,从中任取一球,基本事件为{取中白球}和{取中黑球}
B.在区间[-1,5]上任取一个实数x,使x2-3x+2>0
C.抛一枚质地均匀的硬币,观察其出现正面或反面
D.某人射击中靶或不中靶
3.围棋盒子中有多粒黑子和白子,已知从中取出2粒都是黑子的概率为,都是白子的概率是则从中任意取出2粒恰好是同一色的概率是(
)
A.
B.
C.
D.1
4.如图所示,表示个开关,若在某段时间内,它们正常工作的概率分别为,,,则该系统的可靠性(个开关只要一个开关正常工作即可靠)为(
)
A.0.504
B.0.994
C.0.496
D.0.064
5.有下列说法正确的是(
)
①频数和频率都能反映一个对象在试验总次数中出现的频繁程度;
②在同一次试验中,每个试验结果出现的频数之和等于试验的样本总数;
③在同一次试验中,每个试验结果出现的频率之和不一定等于1;
④概率就是频率.
A.①③
B.①②④
C.①②
D.③④
6.从分别写有1,2,3,4,5的5张卡片中随机抽取1张,放回后再随机抽取1张,则抽得的第一张卡片上的数大于第二张卡片上的数的概率为(
)
A.
B.
C.
D.
7.从装有2个红球和2个黑球的口袋内任取两个球,那么互斥而不对立的事件是(
)
A.至少有一个黑球与都是黑球
B.至少有一个黑球与至少有一个红球
C.恰好有一个黑球与恰好有两个黑球
D.至少有一个黑球与都是红球
8.甲乙两人进行扑克牌得分比赛,甲的三张扑克牌分别记为,,,乙的三张扑克牌分别记为,,.这六张扑克牌的大小顺序为.比赛规则为:每张牌只能出一次,每局比赛双方各出一张牌,共比赛三局,在每局比赛中牌大者得1分,牌小者得0分.若每局比赛之前彼此都不知道对方所出之牌,则六张牌都出完时乙得2分的概率为(
)
A.
B.
C.
D.
9.从数字中随机取两个不同的数,分别记为和,则为整数的概率是(
)
A.
B.
C.
D.
10.从装有两个白球和两个黄球的口袋中任取2个球,以下给出了四组事件:
①至少有1个白球与至少有1个黄球;
②至少有1个黄球与都是黄球;
③恰有1个白球与恰有1个黄球;
④恰有1个白球与都是黄球.
其中互斥而不对立的事件共有(
)
A.0组
B.1组
C.2组
D.3组
二、多选题
11.设,,为三个事件,下列各式意义表述正确的是(
)
A.表示事件不发生且事件和事件同时发生
B.表示事件,,中至少有一个没发生
C.表示事件,至少有一个发生
D.表示事件,,恰有一个发生
12.博览会安排了分别标有序号为“1号”“2号”“3号”的三辆车,等可能随机顺序前往酒店接嘉宾.某嘉宾突发奇想,设计两种乘车方案.方案一:不乘坐第一辆车,若第二辆车的车序号大于第一辆车的车序号,就乘坐此车,否则乘坐第三辆车:方案二:直接乘坐第一辆车.记方案一与方案二坐到“3号”车的概率分别为,,则(
)
A.
B.
C.
D.
13.下图是某市6月1日至14日的空气质量指数趋势图,空气质量指数小于100表示空气质量优良,空气质量指数大于200表示空气重度污染,某人随机选择6月1日至6月13日中的某一天到达该市,并停留2天.下列说法正确的有(
)
A.该市14天空气质量指数的平均值大于100
B.此人到达当日空气质量优良的概率为
C.此人在该市停留期间只有1天空气重度污染的概率为
D.每连续3天计算一次空气质量指数的方差,其中第5天到第7天的方差最大
14.已知甲罐中有四个相同的小球,标号为1,2,3,4;乙罐中有五个相同的小球,标号为1,2,3,5,6,现从甲罐、乙罐中分别随机抽取1个小球,记事件“抽取的两个小球标号之和大于5”,事件“抽取的两个小球标号之积大于8”,则(
)
A.事件发生的概率为
B.事件发生的概率为
C.事件发生的概率为
D.从甲罐中抽到标号为2的小球的概率为
三、填空题
15.某医院一天派出医生下乡医疗,派出医生人数及其概率如下:
医生人数
0
1
2
3
4
5人及以上
概率
0.1
0.16
0.3
0.2
0.2
0.04
则至少派出医生2人的概率是________.
16.设为三个随机事件,若与互斥,与对立,且,,则_____________.
17.在一次全运会男子羽毛球单打比赛中,运动员甲和乙进入了决赛.羽毛球的比赛规则是3局2胜制,假设每局比赛甲获胜的概率为0.6,乙获胜的概率为0.4,利用计算机模拟试验,估计甲获得冠军的概率.为此,用计算机产生1~5之间的随机数,当出现随机数1,2或3时,表示一局比赛甲获胜,其概率为0.6.由于要比赛三局,所以每3个随机数为一组.例如,产生了20组随机数:
423
231
423
344
114
453
525
323
152
342
345
443
512
541
125
342
334
252
324
254
相当于做了20次重复试验,用频率估计甲获得冠军的概率的近似值为_____.
18.如图,把一个表面涂有蓝漆的正方体木块锯成64个完全相同的小正方体,若从中任取一块,则这一块至多有一面涂有蓝漆的概率为_______.
四、解答题
19.先后三次抛掷同一枚硬币,若正面朝上,则记为1;若反面朝上,则记为0.
(1)试写出这个试验的样本空间;
(2)写出“三次结果对应数字之和为1”所包含的样本点;
(3)记事件为“三次结果对应数字之和不小于2”,求.
20.甲?乙两人独立破译一个密码,他们译出的概率分别为和求:
(1)两人都译出的概率;
(2)两人中至少一人译出的概率;
(3)至多有一人译出的概率.
21.某班倡议假期每位学生每天至少锻炼一小时.为了解学生的锻炼情况,对该班全部34名学生在某周的锻炼时间进行了调查,调查结果如下表:
锻炼时长(小时)
5
6
7
8
9
男生人数(人)
1
2
4
3
4
女生人数(人)
3
8
6
2
1
(Ⅰ)试根据上述数据,求这个班级女生在该周的平均锻炼时长;
(Ⅱ)若从锻炼8小时的学生中任选2人参加一项活动,求选到男生和女生各1人的概率;
(Ⅲ)试判断该班男生锻炼时长的方差与女生锻炼时长的方差的大小.(直接写出结果)
22.袋中装有6个形状、大小完全相同的球,其中黑球2个、白球2个、红球2个,规定取出一个黑球记0分,取出一个白球记1分,取出一个红球记2分,抽取这些球的时候,谁也无法看到球的颜色,首先由甲取出3个球,并不再将它们放回原袋中,然后由乙取出剩余的3个球,规定取出球的总积分多者获胜.
(1)求甲、乙成平局的概率;
(2)从概率的角度分析先后取球的顺序是否影响比赛的公平性.
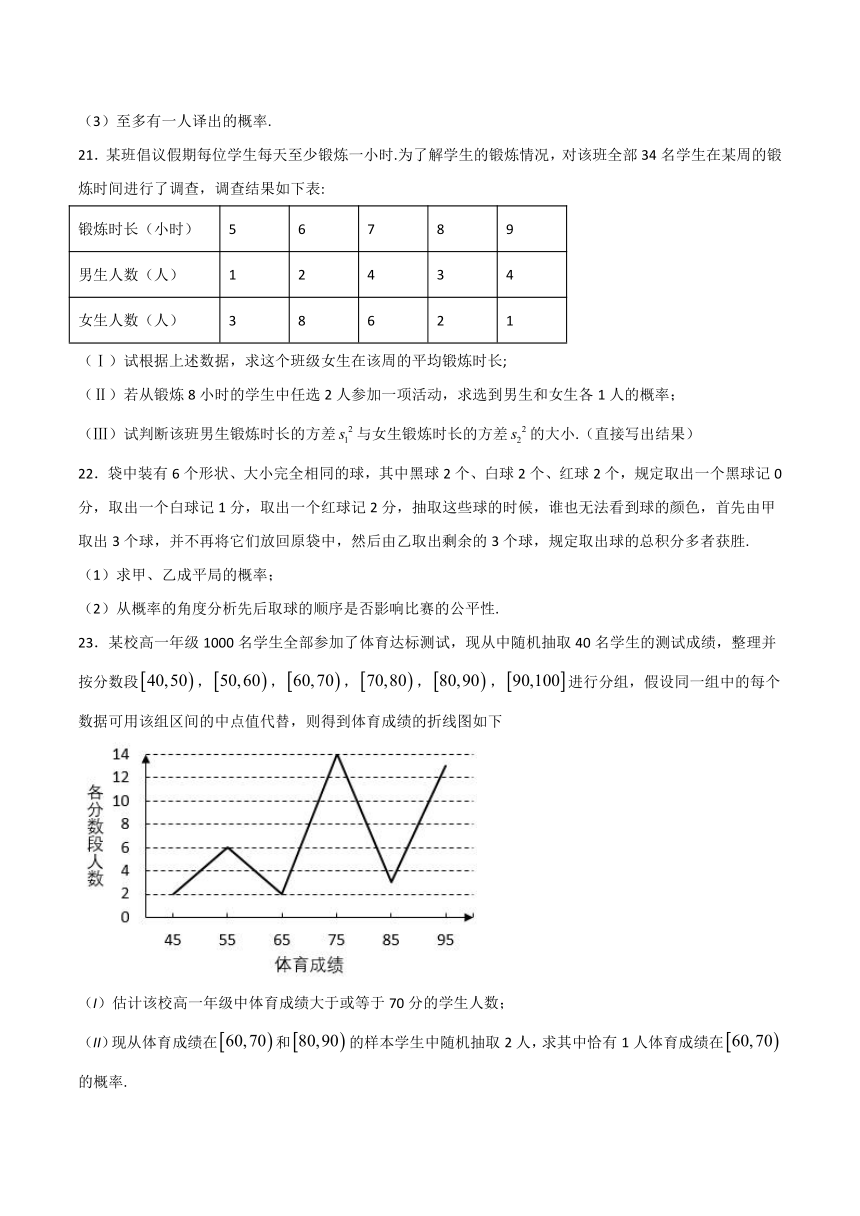
23.某校高一年级1000名学生全部参加了体育达标测试,现从中随机抽取40名学生的测试成绩,整理并按分数段,,,,,进行分组,假设同一组中的每个数据可用该组区间的中点值代替,则得到体育成绩的折线图如下
(I)估计该校高一年级中体育成绩大于或等于70分的学生人数;
(II)现从体育成绩在和的样本学生中随机抽取2人,求其中恰有1人体育成绩在的概率.
参考答案
1.B
所表示的含义是、、这三个事件中至少有一个发生,即可能击中发、发或发.
故选:B.
2.C
【详解】
根据古典概型的两个特征进行判断.
A项中两个基本事件不是等可能的,
B项中基本事件的个数是无限的,
D项中“中靶”与“不中靶”不是等可能的,
C项符合古典概型的两个特征.
3.C
【详解】
从中取出2粒恰好是同一色包含都是黑子或都是白子两个事件,这两个事件是互斥事件,设两粒是同一色为事件,同为黑子为事件,同为白子为事件,
则.
故选:C
4.B
【详解】
三个开关相互独立,三个中只要至少有一个正常工作即可,
由间接法知.
故选:B.
5.C
【详解】
由频率?频数?概率的定义易知①②正确.
故选:C.
6.A
【详解】
从5张卡片中随机抽取1张,放回后再随机抽取1张的情况如图:
基本事件总数为25,
第一张卡片上的数大于第二张卡片上的数的事件数为10,
故所求概率.
故选:A.
7.C
【详解】
A:事件:“至少有一个黑球”与事件:“都是黑球”可以同时发生,如:两个都是黑球,这两个事件不是互斥事件,故错误;
B:事件:“至少有一个黑球”与事件:“至少有一个红球”可以同时发生,如:一个红球一个黑球,故错误;
C:事件:“恰好有一个黑球”与事件:“恰有两个黑球”不能同时发生,但从口袋中任取两个球时还有可能是两个都是红球,两个事件是互斥事件但不是对立事件,故正确
D:事件:“至少有一个黑球”与“都是红球”不能同时发生,但一定会有一个发生,
这两个事件是对立事件,故错误;
故选:C
8.D
【详解】
解:依题意基本事件总数有种;
分别有以下情况:
,,,此时乙得1分;
,,,此时乙得1分;
,,,此时乙得1分;
,,,此时乙得1分;
,,,此时乙得2分;
,,,此时乙得2分;
故六张牌都出完时乙得2分的概率
故选:D
9.B
【详解】
解:从数字中随机取两个不同的数,
则有种选法,有种选法,共有种情况;
则满足为整数的情况如下:
当时,或有种情况;
当时,有种情况;
当或时,则不可能为整数,
故共有种情况,
故为整数的概率是:.
故选:B.
10.B
①中“至少有1个白球”与“至少有1个黄球”可以同时发生,如恰有1个白球和1个黄球,①中的两个事件不是互斥事件.
②中“至少有1个黄球”说明可以是1个白球和1个黄球或2个黄球,则两个事件不互斥.
③中“恰有1个白球”与“恰有1个黄球”,都是指有1个白球和1个黄球,因此两个事件是同一事件.
④中两事件不能同时发生,也可能都不发生,因此两事件是互斥事件,但不是对立事件;
故选:B.
11.ACD
根据题意,依次分析选项:
对于,表示事件不发生且事件和事件同时发生,正确;
对于,表示事件、、至少一个发生,则表示事件都没有发生,错误;
对于,表示事件,至少有一个发生,正确;
对于,表示事件、不发生且事件发生,事件、不发生且事件发生,事件、不发生且事件发生,则表示事件,,恰有一个发生,正确,
故选:.
12.CD
解:分别标有序号为“1号”“2号”“3号”的三辆车,等可能随机顺序前往酒店接嘉宾,
基本事件有:,2,,,3,,,1,,,3,,,1,,,2,,
共6种,
设计两种乘车方案.方案一:不乘坐第一辆车,若第二辆车的车序号大于第一辆车的车序号,
就乘坐此车,否则乘坐第三辆车,
方案一坐到“3号”车包含的基本事件有:,3,,,1,,,3,,有3种,
方案一坐到“3号”车的概率,
方案二:直接乘坐第一辆车,则方案二坐到“3号”车的概率为.
.
故选:.
13.ABCD
【详解】
A.,故正确;
B.在6月1日至6月13日这13天中,1日,2日,3日,7日,12日,13日共6天的空气质量优良,所以此人到达当日空气质量优良的概率为,故正确;
C.6月1日至6月14日连续两天包含的基本事件有13个,此人在该市停留期间只有1天空气重度污染的基本事件是共4个,所以此人在该市停留期间只有1天空气重度污染的概率是,故正确;
D.
空气质量指数趋势图可以看出,从3月5日开始连续三天的空气质量指数方差最大,故正确.
故选:ABCD
14.BC
由题意,从甲罐、乙罐中分别随机抽取1个小球,共包含个基本事件;
“抽取的两个小球标号之和大于5”包含的基本事件有:,,,,,,,,,,,共个基本事件;
“抽取的两个小球标号之积大于8”包含的基本事件有:,,,,,,,,共个基本事件;
即事件是事件的子事件;
因此事件发生的概率为,故A错;
事件包含的基本事件个数为个,所以事件发生的概率为;故B正确;
事件包含的基本事件个数为个,所以事件发生的概率为,故C正确;
从甲罐中抽到标号为2的小球,包含的基本事件为:,,,,共个基本事件,故从甲罐中抽到标号为2的小球的概率为,即D错误.
故选:BC.
15.
【详解】
由题意可知,事件“至少派出医生2人”包含“派出的医生数是2、3、4、5人及以上”,这几个事件是互斥的,概率之和为,故至少派出医生2人的概率是.
故答案为:.
16.
【详解】
与对立,,
与互斥,.
17.
解:由题意可知,20组随机数中甲获胜的有:423
231
423
114
323
152
342
512
125
342
334
252
324有13组,
所以甲获胜的频率为,
所以甲获得冠军的概率的近似值约为,
故答案为:
18.
解:有两面涂有蓝漆的小木块有24个,有三面涂有蓝漆的小木块有8个,
则至多有一面涂有蓝漆的小木块有32个,故.
故答案为:
.
19.
(1)先后三次抛掷同一枚硬币,若正面朝上,则记为1;若反面朝上,则记为0.
其样本空间为;
(2)三次结果对应数字之和为1的样本点为共3个;
(3)三次结果对应数字之和不小于2的样本点为共4个,故.
20.(1);(2);(3).
甲?乙两人独立破译一个密码,他们译出的概率分别为和.
两人都译出的概率为:.
两人中至少一人译出的概率为:
.
至多有一人译出的概率:
.
21.(Ⅰ)小时(Ⅱ)(Ⅲ)
(Ⅰ)这个班级女生在该周的平均锻炼时长为小时
(Ⅱ)由表中数据可知,锻炼8小时的学生中男生有人,记为,女生有人,记为
从中任选2人的所有情况为,,,共种,
其中选到男生和女生各1人的共有种
故选到男生和女生各1人的概率
(Ⅲ)
22.
解:(1)记黑球为1,2号,白球为3,4号,红球为5,6号,
则甲的可能取球共有以下20种情况:123,124,125,126,134,135,136,145,146,156,234,235,236,245,246,256,345,346,356,456,
甲乙平局时都得3分,所以甲取出的三个小球是一黑一白一红,共8种情况,
故平局的概率.
(2)甲获胜时,得分只能是4分或5分,即取出的是2红1白,1红2白,2红1黑共6种情况,
故先取者(甲)获胜的概率,
后取者(乙)获胜的概率,
所以,故先取后取获胜的概率一样.
23.(I)750;(II)
(I)根据折线图可以得到体育成绩大于或等于70分的学生人数为,所以
该校高一年级中体育成绩大于或等于70分的学生人数估计为:.
(II)体育成绩在和的人数分别为、3,分别记为
若随机抽取2人,则所有的基本事件为:
,
故基本事件的总数为.
其中恰有1人体育成绩在的基本事件的个数有6个,
设为:“恰有1人体育成绩在”,则.
试卷第1页,总3页
一、单选题
1.打靶次,事件表示“击中发”,其中、、、.那么表示(
)
A.全部击中
B.至少击中发
C.至少击中发
D.以上均不正确
2.下列试验是古典概型的是(
)
A.口袋中有2个白球和3个黑球,从中任取一球,基本事件为{取中白球}和{取中黑球}
B.在区间[-1,5]上任取一个实数x,使x2-3x+2>0
C.抛一枚质地均匀的硬币,观察其出现正面或反面
D.某人射击中靶或不中靶
3.围棋盒子中有多粒黑子和白子,已知从中取出2粒都是黑子的概率为,都是白子的概率是则从中任意取出2粒恰好是同一色的概率是(
)
A.
B.
C.
D.1
4.如图所示,表示个开关,若在某段时间内,它们正常工作的概率分别为,,,则该系统的可靠性(个开关只要一个开关正常工作即可靠)为(
)
A.0.504
B.0.994
C.0.496
D.0.064
5.有下列说法正确的是(
)
①频数和频率都能反映一个对象在试验总次数中出现的频繁程度;
②在同一次试验中,每个试验结果出现的频数之和等于试验的样本总数;
③在同一次试验中,每个试验结果出现的频率之和不一定等于1;
④概率就是频率.
A.①③
B.①②④
C.①②
D.③④
6.从分别写有1,2,3,4,5的5张卡片中随机抽取1张,放回后再随机抽取1张,则抽得的第一张卡片上的数大于第二张卡片上的数的概率为(
)
A.
B.
C.
D.
7.从装有2个红球和2个黑球的口袋内任取两个球,那么互斥而不对立的事件是(
)
A.至少有一个黑球与都是黑球
B.至少有一个黑球与至少有一个红球
C.恰好有一个黑球与恰好有两个黑球
D.至少有一个黑球与都是红球
8.甲乙两人进行扑克牌得分比赛,甲的三张扑克牌分别记为,,,乙的三张扑克牌分别记为,,.这六张扑克牌的大小顺序为.比赛规则为:每张牌只能出一次,每局比赛双方各出一张牌,共比赛三局,在每局比赛中牌大者得1分,牌小者得0分.若每局比赛之前彼此都不知道对方所出之牌,则六张牌都出完时乙得2分的概率为(
)
A.
B.
C.
D.
9.从数字中随机取两个不同的数,分别记为和,则为整数的概率是(
)
A.
B.
C.
D.
10.从装有两个白球和两个黄球的口袋中任取2个球,以下给出了四组事件:
①至少有1个白球与至少有1个黄球;
②至少有1个黄球与都是黄球;
③恰有1个白球与恰有1个黄球;
④恰有1个白球与都是黄球.
其中互斥而不对立的事件共有(
)
A.0组
B.1组
C.2组
D.3组
二、多选题
11.设,,为三个事件,下列各式意义表述正确的是(
)
A.表示事件不发生且事件和事件同时发生
B.表示事件,,中至少有一个没发生
C.表示事件,至少有一个发生
D.表示事件,,恰有一个发生
12.博览会安排了分别标有序号为“1号”“2号”“3号”的三辆车,等可能随机顺序前往酒店接嘉宾.某嘉宾突发奇想,设计两种乘车方案.方案一:不乘坐第一辆车,若第二辆车的车序号大于第一辆车的车序号,就乘坐此车,否则乘坐第三辆车:方案二:直接乘坐第一辆车.记方案一与方案二坐到“3号”车的概率分别为,,则(
)
A.
B.
C.
D.
13.下图是某市6月1日至14日的空气质量指数趋势图,空气质量指数小于100表示空气质量优良,空气质量指数大于200表示空气重度污染,某人随机选择6月1日至6月13日中的某一天到达该市,并停留2天.下列说法正确的有(
)
A.该市14天空气质量指数的平均值大于100
B.此人到达当日空气质量优良的概率为
C.此人在该市停留期间只有1天空气重度污染的概率为
D.每连续3天计算一次空气质量指数的方差,其中第5天到第7天的方差最大
14.已知甲罐中有四个相同的小球,标号为1,2,3,4;乙罐中有五个相同的小球,标号为1,2,3,5,6,现从甲罐、乙罐中分别随机抽取1个小球,记事件“抽取的两个小球标号之和大于5”,事件“抽取的两个小球标号之积大于8”,则(
)
A.事件发生的概率为
B.事件发生的概率为
C.事件发生的概率为
D.从甲罐中抽到标号为2的小球的概率为
三、填空题
15.某医院一天派出医生下乡医疗,派出医生人数及其概率如下:
医生人数
0
1
2
3
4
5人及以上
概率
0.1
0.16
0.3
0.2
0.2
0.04
则至少派出医生2人的概率是________.
16.设为三个随机事件,若与互斥,与对立,且,,则_____________.
17.在一次全运会男子羽毛球单打比赛中,运动员甲和乙进入了决赛.羽毛球的比赛规则是3局2胜制,假设每局比赛甲获胜的概率为0.6,乙获胜的概率为0.4,利用计算机模拟试验,估计甲获得冠军的概率.为此,用计算机产生1~5之间的随机数,当出现随机数1,2或3时,表示一局比赛甲获胜,其概率为0.6.由于要比赛三局,所以每3个随机数为一组.例如,产生了20组随机数:
423
231
423
344
114
453
525
323
152
342
345
443
512
541
125
342
334
252
324
254
相当于做了20次重复试验,用频率估计甲获得冠军的概率的近似值为_____.
18.如图,把一个表面涂有蓝漆的正方体木块锯成64个完全相同的小正方体,若从中任取一块,则这一块至多有一面涂有蓝漆的概率为_______.
四、解答题
19.先后三次抛掷同一枚硬币,若正面朝上,则记为1;若反面朝上,则记为0.
(1)试写出这个试验的样本空间;
(2)写出“三次结果对应数字之和为1”所包含的样本点;
(3)记事件为“三次结果对应数字之和不小于2”,求.
20.甲?乙两人独立破译一个密码,他们译出的概率分别为和求:
(1)两人都译出的概率;
(2)两人中至少一人译出的概率;
(3)至多有一人译出的概率.
21.某班倡议假期每位学生每天至少锻炼一小时.为了解学生的锻炼情况,对该班全部34名学生在某周的锻炼时间进行了调查,调查结果如下表:
锻炼时长(小时)
5
6
7
8
9
男生人数(人)
1
2
4
3
4
女生人数(人)
3
8
6
2
1
(Ⅰ)试根据上述数据,求这个班级女生在该周的平均锻炼时长;
(Ⅱ)若从锻炼8小时的学生中任选2人参加一项活动,求选到男生和女生各1人的概率;
(Ⅲ)试判断该班男生锻炼时长的方差与女生锻炼时长的方差的大小.(直接写出结果)
22.袋中装有6个形状、大小完全相同的球,其中黑球2个、白球2个、红球2个,规定取出一个黑球记0分,取出一个白球记1分,取出一个红球记2分,抽取这些球的时候,谁也无法看到球的颜色,首先由甲取出3个球,并不再将它们放回原袋中,然后由乙取出剩余的3个球,规定取出球的总积分多者获胜.
(1)求甲、乙成平局的概率;
(2)从概率的角度分析先后取球的顺序是否影响比赛的公平性.
23.某校高一年级1000名学生全部参加了体育达标测试,现从中随机抽取40名学生的测试成绩,整理并按分数段,,,,,进行分组,假设同一组中的每个数据可用该组区间的中点值代替,则得到体育成绩的折线图如下
(I)估计该校高一年级中体育成绩大于或等于70分的学生人数;
(II)现从体育成绩在和的样本学生中随机抽取2人,求其中恰有1人体育成绩在的概率.
参考答案
1.B
所表示的含义是、、这三个事件中至少有一个发生,即可能击中发、发或发.
故选:B.
2.C
【详解】
根据古典概型的两个特征进行判断.
A项中两个基本事件不是等可能的,
B项中基本事件的个数是无限的,
D项中“中靶”与“不中靶”不是等可能的,
C项符合古典概型的两个特征.
3.C
【详解】
从中取出2粒恰好是同一色包含都是黑子或都是白子两个事件,这两个事件是互斥事件,设两粒是同一色为事件,同为黑子为事件,同为白子为事件,
则.
故选:C
4.B
【详解】
三个开关相互独立,三个中只要至少有一个正常工作即可,
由间接法知.
故选:B.
5.C
【详解】
由频率?频数?概率的定义易知①②正确.
故选:C.
6.A
【详解】
从5张卡片中随机抽取1张,放回后再随机抽取1张的情况如图:
基本事件总数为25,
第一张卡片上的数大于第二张卡片上的数的事件数为10,
故所求概率.
故选:A.
7.C
【详解】
A:事件:“至少有一个黑球”与事件:“都是黑球”可以同时发生,如:两个都是黑球,这两个事件不是互斥事件,故错误;
B:事件:“至少有一个黑球”与事件:“至少有一个红球”可以同时发生,如:一个红球一个黑球,故错误;
C:事件:“恰好有一个黑球”与事件:“恰有两个黑球”不能同时发生,但从口袋中任取两个球时还有可能是两个都是红球,两个事件是互斥事件但不是对立事件,故正确
D:事件:“至少有一个黑球”与“都是红球”不能同时发生,但一定会有一个发生,
这两个事件是对立事件,故错误;
故选:C
8.D
【详解】
解:依题意基本事件总数有种;
分别有以下情况:
,,,此时乙得1分;
,,,此时乙得1分;
,,,此时乙得1分;
,,,此时乙得1分;
,,,此时乙得2分;
,,,此时乙得2分;
故六张牌都出完时乙得2分的概率
故选:D
9.B
【详解】
解:从数字中随机取两个不同的数,
则有种选法,有种选法,共有种情况;
则满足为整数的情况如下:
当时,或有种情况;
当时,有种情况;
当或时,则不可能为整数,
故共有种情况,
故为整数的概率是:.
故选:B.
10.B
①中“至少有1个白球”与“至少有1个黄球”可以同时发生,如恰有1个白球和1个黄球,①中的两个事件不是互斥事件.
②中“至少有1个黄球”说明可以是1个白球和1个黄球或2个黄球,则两个事件不互斥.
③中“恰有1个白球”与“恰有1个黄球”,都是指有1个白球和1个黄球,因此两个事件是同一事件.
④中两事件不能同时发生,也可能都不发生,因此两事件是互斥事件,但不是对立事件;
故选:B.
11.ACD
根据题意,依次分析选项:
对于,表示事件不发生且事件和事件同时发生,正确;
对于,表示事件、、至少一个发生,则表示事件都没有发生,错误;
对于,表示事件,至少有一个发生,正确;
对于,表示事件、不发生且事件发生,事件、不发生且事件发生,事件、不发生且事件发生,则表示事件,,恰有一个发生,正确,
故选:.
12.CD
解:分别标有序号为“1号”“2号”“3号”的三辆车,等可能随机顺序前往酒店接嘉宾,
基本事件有:,2,,,3,,,1,,,3,,,1,,,2,,
共6种,
设计两种乘车方案.方案一:不乘坐第一辆车,若第二辆车的车序号大于第一辆车的车序号,
就乘坐此车,否则乘坐第三辆车,
方案一坐到“3号”车包含的基本事件有:,3,,,1,,,3,,有3种,
方案一坐到“3号”车的概率,
方案二:直接乘坐第一辆车,则方案二坐到“3号”车的概率为.
.
故选:.
13.ABCD
【详解】
A.,故正确;
B.在6月1日至6月13日这13天中,1日,2日,3日,7日,12日,13日共6天的空气质量优良,所以此人到达当日空气质量优良的概率为,故正确;
C.6月1日至6月14日连续两天包含的基本事件有13个,此人在该市停留期间只有1天空气重度污染的基本事件是共4个,所以此人在该市停留期间只有1天空气重度污染的概率是,故正确;
D.
空气质量指数趋势图可以看出,从3月5日开始连续三天的空气质量指数方差最大,故正确.
故选:ABCD
14.BC
由题意,从甲罐、乙罐中分别随机抽取1个小球,共包含个基本事件;
“抽取的两个小球标号之和大于5”包含的基本事件有:,,,,,,,,,,,共个基本事件;
“抽取的两个小球标号之积大于8”包含的基本事件有:,,,,,,,,共个基本事件;
即事件是事件的子事件;
因此事件发生的概率为,故A错;
事件包含的基本事件个数为个,所以事件发生的概率为;故B正确;
事件包含的基本事件个数为个,所以事件发生的概率为,故C正确;
从甲罐中抽到标号为2的小球,包含的基本事件为:,,,,共个基本事件,故从甲罐中抽到标号为2的小球的概率为,即D错误.
故选:BC.
15.
【详解】
由题意可知,事件“至少派出医生2人”包含“派出的医生数是2、3、4、5人及以上”,这几个事件是互斥的,概率之和为,故至少派出医生2人的概率是.
故答案为:.
16.
【详解】
与对立,,
与互斥,.
17.
解:由题意可知,20组随机数中甲获胜的有:423
231
423
114
323
152
342
512
125
342
334
252
324有13组,
所以甲获胜的频率为,
所以甲获得冠军的概率的近似值约为,
故答案为:
18.
解:有两面涂有蓝漆的小木块有24个,有三面涂有蓝漆的小木块有8个,
则至多有一面涂有蓝漆的小木块有32个,故.
故答案为:
.
19.
(1)先后三次抛掷同一枚硬币,若正面朝上,则记为1;若反面朝上,则记为0.
其样本空间为;
(2)三次结果对应数字之和为1的样本点为共3个;
(3)三次结果对应数字之和不小于2的样本点为共4个,故.
20.(1);(2);(3).
甲?乙两人独立破译一个密码,他们译出的概率分别为和.
两人都译出的概率为:.
两人中至少一人译出的概率为:
.
至多有一人译出的概率:
.
21.(Ⅰ)小时(Ⅱ)(Ⅲ)
(Ⅰ)这个班级女生在该周的平均锻炼时长为小时
(Ⅱ)由表中数据可知,锻炼8小时的学生中男生有人,记为,女生有人,记为
从中任选2人的所有情况为,,,共种,
其中选到男生和女生各1人的共有种
故选到男生和女生各1人的概率
(Ⅲ)
22.
解:(1)记黑球为1,2号,白球为3,4号,红球为5,6号,
则甲的可能取球共有以下20种情况:123,124,125,126,134,135,136,145,146,156,234,235,236,245,246,256,345,346,356,456,
甲乙平局时都得3分,所以甲取出的三个小球是一黑一白一红,共8种情况,
故平局的概率.
(2)甲获胜时,得分只能是4分或5分,即取出的是2红1白,1红2白,2红1黑共6种情况,
故先取者(甲)获胜的概率,
后取者(乙)获胜的概率,
所以,故先取后取获胜的概率一样.
23.(I)750;(II)
(I)根据折线图可以得到体育成绩大于或等于70分的学生人数为,所以
该校高一年级中体育成绩大于或等于70分的学生人数估计为:.
(II)体育成绩在和的人数分别为、3,分别记为
若随机抽取2人,则所有的基本事件为:
,
故基本事件的总数为.
其中恰有1人体育成绩在的基本事件的个数有6个,
设为:“恰有1人体育成绩在”,则.
试卷第1页,总3页
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
