2021-2022七上第三章 3.1.1 一元一次方程课件(共39张PPT)
文档属性
| 名称 | 2021-2022七上第三章 3.1.1 一元一次方程课件(共39张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-07 00:00:00 | ||
图片预览






文档简介
(共39张PPT)
3.1
从算式到方程
3.1.1
一元一次方程
人教版
数学
七年级
上册
汽车匀速行驶途经王家庄、青山、秀水三地的时间如表所示,翠湖在青山、秀水两地之间,距青山50千米,距秀水70千米.王家庄到翠湖的路程有多远?
地名
时间
王家庄
10:00
青山
13:00
秀水
15:00
导入新知
你会用方程方法解决这个实际问题吗?
汽车匀速行驶途经王家庄、青山、秀水三地的时间如表所示,翠湖在青山、秀水两地之间,距青山50千米,距秀水70千米.王家庄到翠湖的路程有多远?
地名
时间
王家庄
10:00
青山
13:00
秀水
15:00
用算术方法解决
导入新知
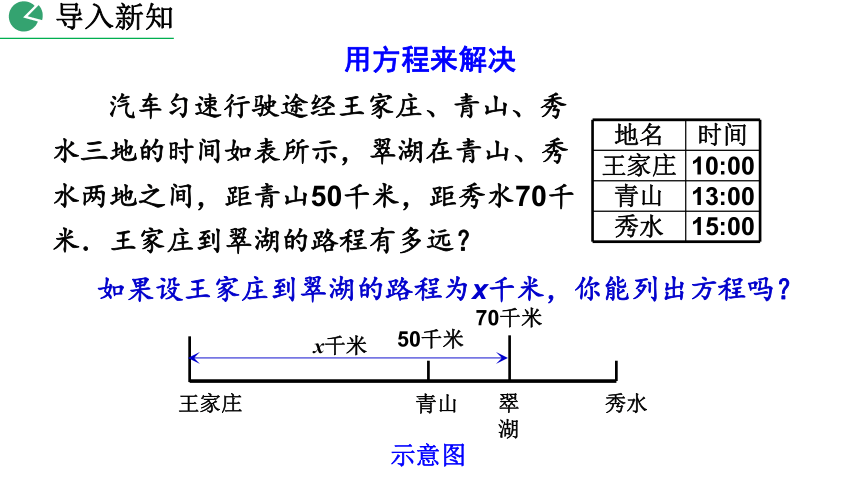
如果设王家庄到翠湖的路程为x千米,你能列出方程吗?
汽车匀速行驶途经王家庄、青山、秀水三地的时间如表所示,翠湖在青山、秀水两地之间,距青山50千米,距秀水70千米.王家庄到翠湖的路程有多远?
地名
时间
王家庄
10:00
青山
13:00
秀水
15:00
王家庄
青山
翠湖
秀水
50千米
70千米
x千米
示意图
用方程来解决
导入新知
2.通过实际问题的分析找出等量关系列出方程.
3.
通过列方程的过程,感受方程作为刻画现实世界有效模型的意义,从而体会数学的方程模型思想.
素养目标
1.
理解方程及一元一次方程的概念,会检验一个数是不是方程的解.
在小学,我们已经见过像
2x=50,3x+1=4,5x-7=8
这样简单的方程,还有下面列出的式子:
方程
含有未知数的等式
又如:
|x+5|
=2
x2
–8x+2=0
x+1=2x-5
6x-11=12
知识点
1
方程和一元一次方程的概念
探究新知
如:
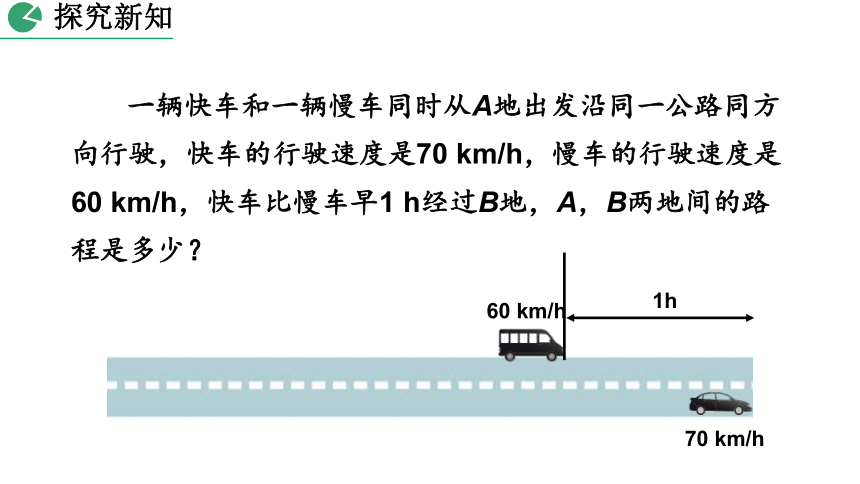
一辆快车和一辆慢车同时从A地出发沿同一公路同方向行驶,快车的行驶速度是70
km/h,慢车的行驶速度是60
km/h,快车比慢车早1
h经过B地,A,B两地间的路程是多少?
1h
60
km/h
70
km/h
探究新知
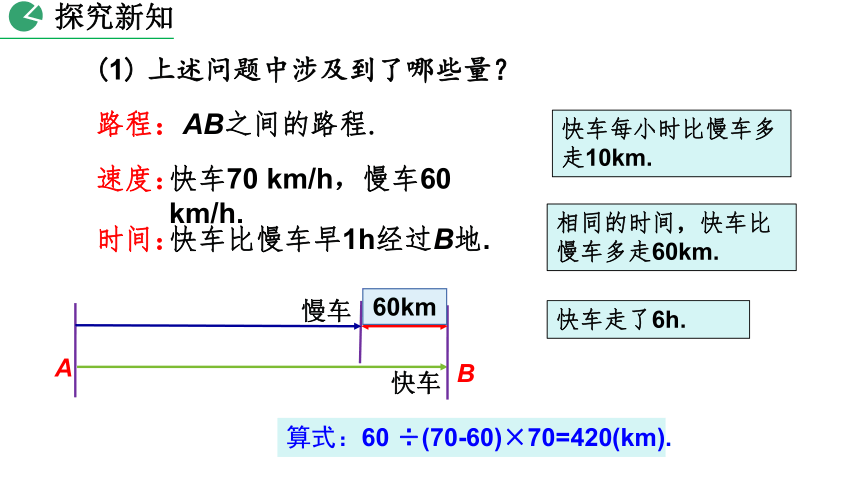
(1)
上述问题中涉及到了哪些量?
快车70
km/h,慢车60
km/h.
快车比慢车早1h经过B地.
AB之间的路程.
速度:
时间:
路程:
A
B
快车
慢车
1h
快车每小时比慢车多走10km.
60km
相同的时间,快车比慢车多走60km.
快车走了6h.
算式:60
÷(70-60)×70=420(km).
探究新知
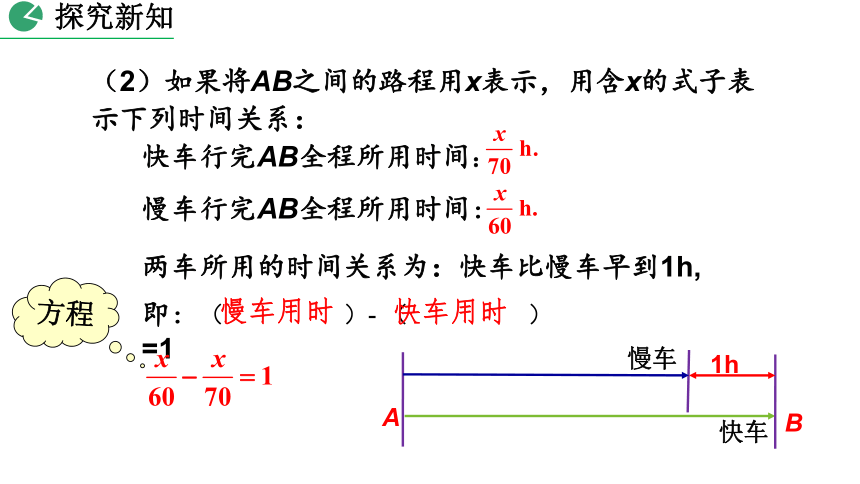
(2)如果将AB之间的路程用x表示,用含x的式子表示下列时间关系:
快车行完AB全程所用时间:
慢车行完AB全程所用时间:
两车所用的时间关系为:快车比慢车早到1h,
即:(
)-
(
)=1
慢车用时
快车用时
A
B
快车
慢车
1h
方程
探究新知
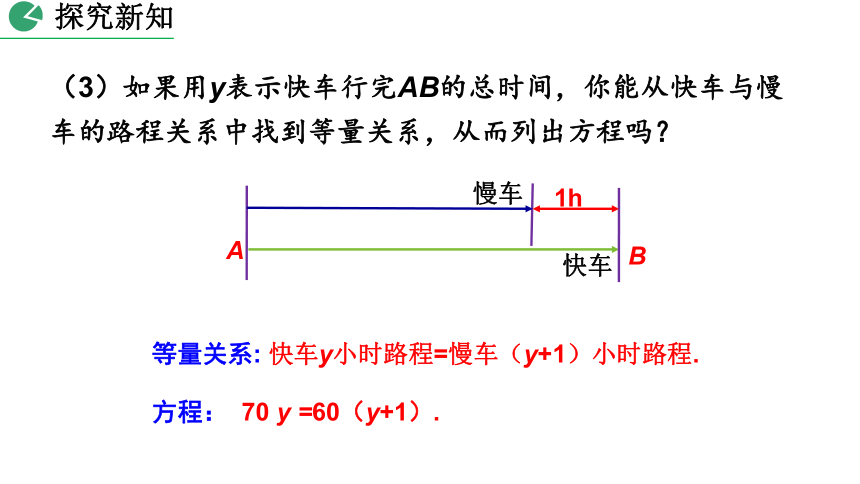
(3)如果用y表示快车行完AB的总时间,你能从快车与慢车的路程关系中找到等量关系,从而列出方程吗?
方程:
70
y
=60(y+1).
等量关系:
快车y小时路程=慢车(y+1)小时路程.
A
B
快车
慢车
1h
探究新知
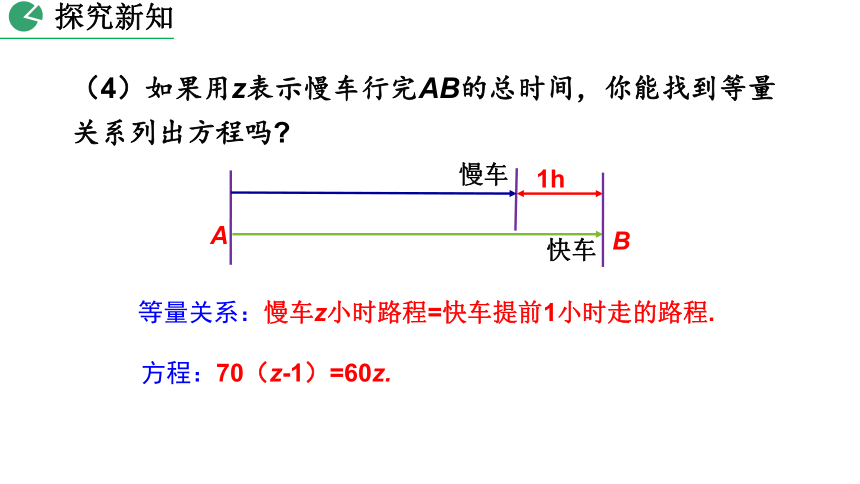
(4)如果用z表示慢车行完AB的总时间,你能找到等量关系列出方程吗?
方程:70(z-1)=60z.
等量关系:慢车z小时路程=快车提前1小时走的路程.
A
B
快车
慢车
1h
探究新知
比较:列算式和列方程.
列算式:列出的算式表示解题的计算过程,
只能用已知数.对于较复杂的问题,列算式比较困难.
列方程:方程是根据题中的等量关系列出的等式.
既可用已知数,又可用未知数,解决问题比较方便.
探究新知
从算式到方程是数学的进步!
观察下列方程,它们有什么共同点?
70
y=60(y+1)
70(z-1)=60z
问题1:每个方程中,各含有几个未知数?
问题2:说一说每个方程中未知数的次数.
问题3:等号两边的式子有什么共同点?
1个
1次
都是整式
探究新知
这样的方程叫做一元一次方程.
等号两边都是整式,
(一次)
只含有一个未知数,
(一元)
未知数的次数都是1,
探究新知
一元一次方程
例1
哪些是一元一次方程?
(1)
;
(2)
;
(3)
;
(4)
;
(5)
;
(6)
;
(7)
.
(4)(5)是一元一次方程.
解析:
只含有一个未知数(元),未知数的次数都是1(次)的整式方程叫做一元一次方程.
素养考点
1
一元一次方程的识别
不是等式
不是整式方程
是不等式,不是方程
未知数的次数是2
含有两个未知数
探究新知
√
√
(1)3y-7
;
(2)
;
(3)16y-7=9-2y
;
(4)7y-y2=12;
(5)-4.5y-12=x-10
;
(6)3b-3<10
;
(7)
.
7a+8=10
下列哪些是一元一次方程?
巩固练习
例2
若关于x的方程
是一元一次方程,则
n
的值为
.
【变式题】
方程
是关于x的一元一次方程,则
m=
.
2或-2
1
方法总结:一元一次方程中求字母的值,需谨记两个条件:
①未知数的次数为1;②未知数的系数不为0.
利用一元一次方程的定义求字母的值
素养考点
2
探究新知
加了限制条件,需进行取舍.
方程3x5-2k
-8=0是关于x的一元一次方程,则k=_____.
2
方程x|m|
+4=0是关于x的一元一次方程,则m=_____.
方程(m-1)x
-2=0是关于x的一元一次方程,则m_____.
1或-1
≠1
巩固练习
例3
根据下列问题,设未知数并列出方程:
(1)
用一根长24
cm的铁丝围成一个正方形,正方形的边长是多少?
解:设正方形的边长为x
cm.
等量关系:正方形边长×4=周长,
列方程:
.
x
根据实际问题建立方程模型
素养考点
3
探究新知
(2)
一台计算机已使用1700
h,预计每月再使用150
h,经过多少月这台计算机的使用时间达到规定的检修时间2450
h?
解:设x月后这台计算机的使用时间达到2450h.
等量关系:已用时间+再用时间=检修时间,
列方程:
.
.
探究新知
(3)
某校女生占全体学生数的52%,比男生多8人,这个学校一共有多少学生?
解:设这个学校的学生人数为x,那么女生人数为
0.52x,男生人数为(1-
0.52)x.
列方程:0.52x-
(1-0.52)x=8.
等量关系:女生人数-
男生人数=8,
探究新知
例4
某文具店一支铅笔的售价为1.2元,一支圆珠笔的售价为2元.该店在“6·1”儿童节举行文具优惠售卖活动,铅笔按原价打8折出售,圆珠笔按原价打9折出售,结果两种笔共卖出60支,卖得金额87元.求卖出铅笔的支数.
解:设卖出铅笔x支,则卖出圆珠笔(60-x)支.
等量关系:x支铅笔的售价+(60-x)支圆珠笔的售价=87
列方程:
.
探究新知
分析实际问题中的数量关系,利用其中的相等关系列出方程,是用数学解决实际问题的一种方法.
思考:1.
怎样将一个实际问题转化为方程问题?
2.
列方程的依据是什么?
设未知数列方程
一元一次方程
抓关键句子找等量关系
实际问题
探究新知
(1)某长方形足球场的周长为310米,长和宽之差为25米,求这个足球场的宽.
解:设这个足球场的宽为x米,依题意,得
2x+2(x+25)=310.
解:设从甲队调给乙队x人,依题意,得
54-x=
(66+x).
(2)甲队有54人,乙队有66人,问从甲队调给乙队几人,可使甲队的人数是乙队人数的三分之一
?
根据下列问题,设出未知数,列出方程:
巩固练习
对于方程4x=24,容易知道
x
=
6可以使等式成立,
对
于方程
170+15x
=245,你知道
x
等于什么时,等式成立吗?我们来试一试.
x
1
2
3
4
5
6
…
…
我们知道当x=5时,170+15x的值是245,所以方程
170+15x
=
245中的未知数的值应是5.
185
200
215
230
245
260
170+15x
方程的解
知识点
2
探究新知
2x-3=5x-15
x=4是方程2x-3=5x-15的解.
左边=2×3-3
=
3,
右边=5×3-15
=
0,
x=
4,
5,
6时呢?
x=3是不是方程的解呢?
把x=3代入方程:
因为左边≠右边,
所以x=3不是方程的解.
解:
探究新知
使方程左右两边相等的未知数的值叫方程的解.求方程解的过程叫做解方程.
x=420是
方程的解吗?
探究新知
方程的解
例
x=1000和x=2000中哪一个是方程
0.52x-(1-0.52)x=80
的解?
解:当x=1000时,
方程左边=0.52×1000-(1-0.52)×1000=520-480=40,
右边=80,左边≠右边,所以x=1000不是此方程的解.
当
x=2000时,
方程左边=
0.52×2000-(1-0.52)×2000=1040-960=80,
右边=80,左边=右边,所以x=2000是此方程的解.
方程的解的识别
素养考点
探究新知
1.
将数值代入方程左边进行计算;
2.
将数值代入方程右边进行计算;
3.
若左边=右边,则是方程的解,反之,则不是.
判断一个数值是不是方程的解的步骤:
方法归纳
探究新知
下列一元一次方程中,解为
的是(
)
A.
B.
C.
D.
B
巩固练习
由于受H7N9禽流感的影响,我市某城区今年2月份鸡的价格比1月份下降a%,3月份比2月份下降b%,已知1月份鸡的价格为24元/千克.设3月份鸡的价格为m元/千克,则( )
A.
m=24(1-a%-b%)
B.
m=24(1-a%)b%
C.
m=24-a%-b%
D.
m=24(1-a%)(1-b%)
D
连接中考
2.
若
x
=1是方程x2
-2mx
+1=0的一个解,则m的值为(
)
A.
0
B.
2
C.
1
D.
-1
1.
x
=1是下列哪个方程的解
(
)
A.
B.
C.
D.
B
C
基础巩固题
课堂检测
3.
下列方程:
;
;
;
;
其中是方程的是
,是一元一次方程的
是
.(填序号)
①②③④⑤
②③
课堂检测
根据下列问题,找出等量关系,设未知数列出方程,并指出其是不是一元一次方程.
(1)环形跑道一周长400m,沿跑道跑多少周,可以跑3000m?
解:设沿跑道跑x周.
400x=3000,
是一元一次方程.
能力提升题
课堂检测
一周长×周数=总路程
(2)甲种铅笔每支0.3
元,乙种铅笔每支0.6
元,用
9
元钱买了两种铅笔共20
支,两种铅笔各买了多少支?
解:设甲种铅笔买了x支,乙种铅笔买了(20-x)支.
0.3x+0.6(20-x)=9,
是一元一次方程.
课堂检测
(3)一个梯形的下底比上底多2
cm,高是5
cm,面
积是40
cm2,求上底.
解:设上底为x
cm,则下底为(x+2)cm.
,
是一元一次方程.
(上底+下底)×高=梯形面积
课堂检测
解:因为方程
是关于x的一元
一次方程,
所以|m|-1
=
1,且m-2≠0,得m
=
-2.
所以原方程为-4x+3
=
-7.
已知方程
是关于x的一元一次方程,求m的值,并写出其方程.
拓广探索题
课堂检测
方程
方程
建立方程模型
含有未知数的等式叫做方程.
一元一次方程
只含有一个未知数,未知数的次数是1,等号两边都是整式,这样的方程叫做一元一次方程.
方程的解
解方程就是求出使方程中等号两边相等的未知数的值,这个值就是方程的解.
实际问题
一元一次方程
设未知数
找等量关系
列方程
课堂小结
课后作业
作业
内容
教材作业
从课后习题中选取
自主安排
配套练习册练习
3.1
从算式到方程
3.1.1
一元一次方程
人教版
数学
七年级
上册
汽车匀速行驶途经王家庄、青山、秀水三地的时间如表所示,翠湖在青山、秀水两地之间,距青山50千米,距秀水70千米.王家庄到翠湖的路程有多远?
地名
时间
王家庄
10:00
青山
13:00
秀水
15:00
导入新知
你会用方程方法解决这个实际问题吗?
汽车匀速行驶途经王家庄、青山、秀水三地的时间如表所示,翠湖在青山、秀水两地之间,距青山50千米,距秀水70千米.王家庄到翠湖的路程有多远?
地名
时间
王家庄
10:00
青山
13:00
秀水
15:00
用算术方法解决
导入新知
如果设王家庄到翠湖的路程为x千米,你能列出方程吗?
汽车匀速行驶途经王家庄、青山、秀水三地的时间如表所示,翠湖在青山、秀水两地之间,距青山50千米,距秀水70千米.王家庄到翠湖的路程有多远?
地名
时间
王家庄
10:00
青山
13:00
秀水
15:00
王家庄
青山
翠湖
秀水
50千米
70千米
x千米
示意图
用方程来解决
导入新知
2.通过实际问题的分析找出等量关系列出方程.
3.
通过列方程的过程,感受方程作为刻画现实世界有效模型的意义,从而体会数学的方程模型思想.
素养目标
1.
理解方程及一元一次方程的概念,会检验一个数是不是方程的解.
在小学,我们已经见过像
2x=50,3x+1=4,5x-7=8
这样简单的方程,还有下面列出的式子:
方程
含有未知数的等式
又如:
|x+5|
=2
x2
–8x+2=0
x+1=2x-5
6x-11=12
知识点
1
方程和一元一次方程的概念
探究新知
如:
一辆快车和一辆慢车同时从A地出发沿同一公路同方向行驶,快车的行驶速度是70
km/h,慢车的行驶速度是60
km/h,快车比慢车早1
h经过B地,A,B两地间的路程是多少?
1h
60
km/h
70
km/h
探究新知
(1)
上述问题中涉及到了哪些量?
快车70
km/h,慢车60
km/h.
快车比慢车早1h经过B地.
AB之间的路程.
速度:
时间:
路程:
A
B
快车
慢车
1h
快车每小时比慢车多走10km.
60km
相同的时间,快车比慢车多走60km.
快车走了6h.
算式:60
÷(70-60)×70=420(km).
探究新知
(2)如果将AB之间的路程用x表示,用含x的式子表示下列时间关系:
快车行完AB全程所用时间:
慢车行完AB全程所用时间:
两车所用的时间关系为:快车比慢车早到1h,
即:(
)-
(
)=1
慢车用时
快车用时
A
B
快车
慢车
1h
方程
探究新知
(3)如果用y表示快车行完AB的总时间,你能从快车与慢车的路程关系中找到等量关系,从而列出方程吗?
方程:
70
y
=60(y+1).
等量关系:
快车y小时路程=慢车(y+1)小时路程.
A
B
快车
慢车
1h
探究新知
(4)如果用z表示慢车行完AB的总时间,你能找到等量关系列出方程吗?
方程:70(z-1)=60z.
等量关系:慢车z小时路程=快车提前1小时走的路程.
A
B
快车
慢车
1h
探究新知
比较:列算式和列方程.
列算式:列出的算式表示解题的计算过程,
只能用已知数.对于较复杂的问题,列算式比较困难.
列方程:方程是根据题中的等量关系列出的等式.
既可用已知数,又可用未知数,解决问题比较方便.
探究新知
从算式到方程是数学的进步!
观察下列方程,它们有什么共同点?
70
y=60(y+1)
70(z-1)=60z
问题1:每个方程中,各含有几个未知数?
问题2:说一说每个方程中未知数的次数.
问题3:等号两边的式子有什么共同点?
1个
1次
都是整式
探究新知
这样的方程叫做一元一次方程.
等号两边都是整式,
(一次)
只含有一个未知数,
(一元)
未知数的次数都是1,
探究新知
一元一次方程
例1
哪些是一元一次方程?
(1)
;
(2)
;
(3)
;
(4)
;
(5)
;
(6)
;
(7)
.
(4)(5)是一元一次方程.
解析:
只含有一个未知数(元),未知数的次数都是1(次)的整式方程叫做一元一次方程.
素养考点
1
一元一次方程的识别
不是等式
不是整式方程
是不等式,不是方程
未知数的次数是2
含有两个未知数
探究新知
√
√
(1)3y-7
;
(2)
;
(3)16y-7=9-2y
;
(4)7y-y2=12;
(5)-4.5y-12=x-10
;
(6)3b-3<10
;
(7)
.
7a+8=10
下列哪些是一元一次方程?
巩固练习
例2
若关于x的方程
是一元一次方程,则
n
的值为
.
【变式题】
方程
是关于x的一元一次方程,则
m=
.
2或-2
1
方法总结:一元一次方程中求字母的值,需谨记两个条件:
①未知数的次数为1;②未知数的系数不为0.
利用一元一次方程的定义求字母的值
素养考点
2
探究新知
加了限制条件,需进行取舍.
方程3x5-2k
-8=0是关于x的一元一次方程,则k=_____.
2
方程x|m|
+4=0是关于x的一元一次方程,则m=_____.
方程(m-1)x
-2=0是关于x的一元一次方程,则m_____.
1或-1
≠1
巩固练习
例3
根据下列问题,设未知数并列出方程:
(1)
用一根长24
cm的铁丝围成一个正方形,正方形的边长是多少?
解:设正方形的边长为x
cm.
等量关系:正方形边长×4=周长,
列方程:
.
x
根据实际问题建立方程模型
素养考点
3
探究新知
(2)
一台计算机已使用1700
h,预计每月再使用150
h,经过多少月这台计算机的使用时间达到规定的检修时间2450
h?
解:设x月后这台计算机的使用时间达到2450h.
等量关系:已用时间+再用时间=检修时间,
列方程:
.
.
探究新知
(3)
某校女生占全体学生数的52%,比男生多8人,这个学校一共有多少学生?
解:设这个学校的学生人数为x,那么女生人数为
0.52x,男生人数为(1-
0.52)x.
列方程:0.52x-
(1-0.52)x=8.
等量关系:女生人数-
男生人数=8,
探究新知
例4
某文具店一支铅笔的售价为1.2元,一支圆珠笔的售价为2元.该店在“6·1”儿童节举行文具优惠售卖活动,铅笔按原价打8折出售,圆珠笔按原价打9折出售,结果两种笔共卖出60支,卖得金额87元.求卖出铅笔的支数.
解:设卖出铅笔x支,则卖出圆珠笔(60-x)支.
等量关系:x支铅笔的售价+(60-x)支圆珠笔的售价=87
列方程:
.
探究新知
分析实际问题中的数量关系,利用其中的相等关系列出方程,是用数学解决实际问题的一种方法.
思考:1.
怎样将一个实际问题转化为方程问题?
2.
列方程的依据是什么?
设未知数列方程
一元一次方程
抓关键句子找等量关系
实际问题
探究新知
(1)某长方形足球场的周长为310米,长和宽之差为25米,求这个足球场的宽.
解:设这个足球场的宽为x米,依题意,得
2x+2(x+25)=310.
解:设从甲队调给乙队x人,依题意,得
54-x=
(66+x).
(2)甲队有54人,乙队有66人,问从甲队调给乙队几人,可使甲队的人数是乙队人数的三分之一
?
根据下列问题,设出未知数,列出方程:
巩固练习
对于方程4x=24,容易知道
x
=
6可以使等式成立,
对
于方程
170+15x
=245,你知道
x
等于什么时,等式成立吗?我们来试一试.
x
1
2
3
4
5
6
…
…
我们知道当x=5时,170+15x的值是245,所以方程
170+15x
=
245中的未知数的值应是5.
185
200
215
230
245
260
170+15x
方程的解
知识点
2
探究新知
2x-3=5x-15
x=4是方程2x-3=5x-15的解.
左边=2×3-3
=
3,
右边=5×3-15
=
0,
x=
4,
5,
6时呢?
x=3是不是方程的解呢?
把x=3代入方程:
因为左边≠右边,
所以x=3不是方程的解.
解:
探究新知
使方程左右两边相等的未知数的值叫方程的解.求方程解的过程叫做解方程.
x=420是
方程的解吗?
探究新知
方程的解
例
x=1000和x=2000中哪一个是方程
0.52x-(1-0.52)x=80
的解?
解:当x=1000时,
方程左边=0.52×1000-(1-0.52)×1000=520-480=40,
右边=80,左边≠右边,所以x=1000不是此方程的解.
当
x=2000时,
方程左边=
0.52×2000-(1-0.52)×2000=1040-960=80,
右边=80,左边=右边,所以x=2000是此方程的解.
方程的解的识别
素养考点
探究新知
1.
将数值代入方程左边进行计算;
2.
将数值代入方程右边进行计算;
3.
若左边=右边,则是方程的解,反之,则不是.
判断一个数值是不是方程的解的步骤:
方法归纳
探究新知
下列一元一次方程中,解为
的是(
)
A.
B.
C.
D.
B
巩固练习
由于受H7N9禽流感的影响,我市某城区今年2月份鸡的价格比1月份下降a%,3月份比2月份下降b%,已知1月份鸡的价格为24元/千克.设3月份鸡的价格为m元/千克,则( )
A.
m=24(1-a%-b%)
B.
m=24(1-a%)b%
C.
m=24-a%-b%
D.
m=24(1-a%)(1-b%)
D
连接中考
2.
若
x
=1是方程x2
-2mx
+1=0的一个解,则m的值为(
)
A.
0
B.
2
C.
1
D.
-1
1.
x
=1是下列哪个方程的解
(
)
A.
B.
C.
D.
B
C
基础巩固题
课堂检测
3.
下列方程:
;
;
;
;
其中是方程的是
,是一元一次方程的
是
.(填序号)
①②③④⑤
②③
课堂检测
根据下列问题,找出等量关系,设未知数列出方程,并指出其是不是一元一次方程.
(1)环形跑道一周长400m,沿跑道跑多少周,可以跑3000m?
解:设沿跑道跑x周.
400x=3000,
是一元一次方程.
能力提升题
课堂检测
一周长×周数=总路程
(2)甲种铅笔每支0.3
元,乙种铅笔每支0.6
元,用
9
元钱买了两种铅笔共20
支,两种铅笔各买了多少支?
解:设甲种铅笔买了x支,乙种铅笔买了(20-x)支.
0.3x+0.6(20-x)=9,
是一元一次方程.
课堂检测
(3)一个梯形的下底比上底多2
cm,高是5
cm,面
积是40
cm2,求上底.
解:设上底为x
cm,则下底为(x+2)cm.
,
是一元一次方程.
(上底+下底)×高=梯形面积
课堂检测
解:因为方程
是关于x的一元
一次方程,
所以|m|-1
=
1,且m-2≠0,得m
=
-2.
所以原方程为-4x+3
=
-7.
已知方程
是关于x的一元一次方程,求m的值,并写出其方程.
拓广探索题
课堂检测
方程
方程
建立方程模型
含有未知数的等式叫做方程.
一元一次方程
只含有一个未知数,未知数的次数是1,等号两边都是整式,这样的方程叫做一元一次方程.
方程的解
解方程就是求出使方程中等号两边相等的未知数的值,这个值就是方程的解.
实际问题
一元一次方程
设未知数
找等量关系
列方程
课堂小结
课后作业
作业
内容
教材作业
从课后习题中选取
自主安排
配套练习册练习
