(苏教版)溧水县第二高级中学数学教学案必修3:第19课时(线性回归方程的应用)
文档属性
| 名称 | (苏教版)溧水县第二高级中学数学教学案必修3:第19课时(线性回归方程的应用) |
|
|
| 格式 | zip | ||
| 文件大小 | 20.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-06-22 00:00:00 | ||
图片预览


文档简介
总 课 题 统 计 总课时 第19课时
分 课 题 线性回归方程的应用 分课时 第 2 课时
教学目标 会求解回归直线方程,并学会做出估计.
重点难点 求解回归直线方程.
例题剖析
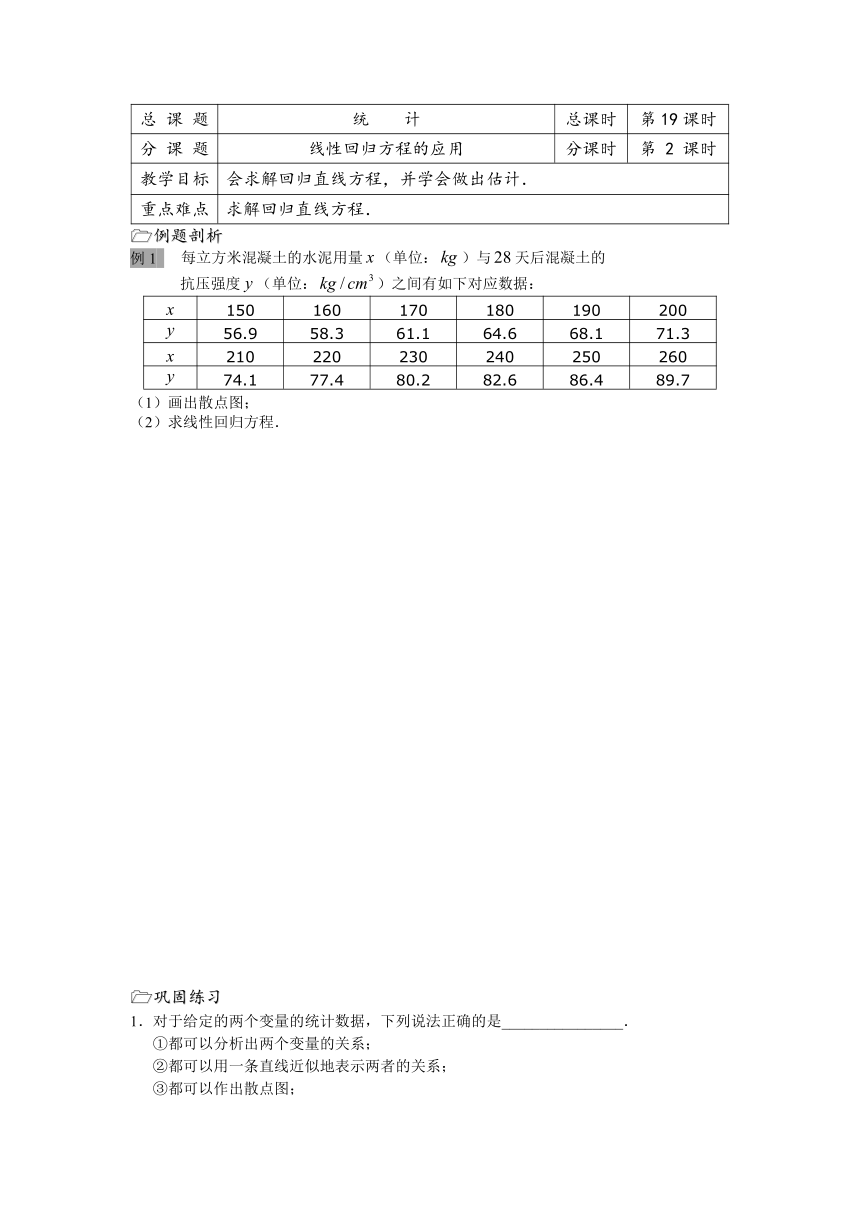
每立方米混凝土的水泥用量(单位:)与天后混凝土的
抗压强度(单位:)之间有如下对应数据:
150 160 170 180 190 200
56.9 58.3 61.1 64.6 68.1 71.3
210 220 230 240 250 260
74.1 77.4 80.2 82.6 86.4 89.7
(1)画出散点图;
(2)求线性回归方程.
巩固练习
1.对于给定的两个变量的统计数据,下列说法正确的是________________.
①都可以分析出两个变量的关系;
②都可以用一条直线近似地表示两者的关系;
③都可以作出散点图;
④都可以用确定的表达式表示两者的关系.
2.假设关于某设备的使用年限(年)和所支出的维修费用(万元),
有如下的统计资料:
使用年限(年) 2 3 4 5 6
维修费用(万元) 2.2 3.8 5.5 6.5 7.0
(1)试求线性回归方程;
(2)估计使用年限为年时,维修费用是多少?
课堂小结
会求解回归直线方程,并学会做出估计.
课后训练
班级:高二( )班 姓名:____________
一 基础题
1.在研究硝酸钠的可溶性程度时,对不同的温度观测它在水中的溶解度,得观察数据:
温度 0 10 20 50 70
溶解度 66.7 76.0 85.0 112.3 128.0
则由此得到的回归直线的斜率是______________.
2.以下是收集到的新房屋的销售价格与房屋的大小的数据:
房屋大小() 115 110 80 135 105
销售价格(万元) 24.8 21.6 18.4 29.2 22
(1)画出散点图;
(2)求线性回归方程,并估计买的新房的费用.
二 提高题
3.以家庭为单位,某中商品年需求量与该商品价格之间的一组调查数据如下表:
价格(元) 5 2 2 2.3 2.5 2.6 2.8 3 3.3 3.5
需求量() 1 3.5 3 2.7 2.4 2.5 2 1.5 1.2 1.2
(1)画出散点图;
(2)求线性回归方程,并估计价格为元时该商品的需求量.
.精品资料。欢迎使用。 ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
例1
分 课 题 线性回归方程的应用 分课时 第 2 课时
教学目标 会求解回归直线方程,并学会做出估计.
重点难点 求解回归直线方程.
例题剖析
每立方米混凝土的水泥用量(单位:)与天后混凝土的
抗压强度(单位:)之间有如下对应数据:
150 160 170 180 190 200
56.9 58.3 61.1 64.6 68.1 71.3
210 220 230 240 250 260
74.1 77.4 80.2 82.6 86.4 89.7
(1)画出散点图;
(2)求线性回归方程.
巩固练习
1.对于给定的两个变量的统计数据,下列说法正确的是________________.
①都可以分析出两个变量的关系;
②都可以用一条直线近似地表示两者的关系;
③都可以作出散点图;
④都可以用确定的表达式表示两者的关系.
2.假设关于某设备的使用年限(年)和所支出的维修费用(万元),
有如下的统计资料:
使用年限(年) 2 3 4 5 6
维修费用(万元) 2.2 3.8 5.5 6.5 7.0
(1)试求线性回归方程;
(2)估计使用年限为年时,维修费用是多少?
课堂小结
会求解回归直线方程,并学会做出估计.
课后训练
班级:高二( )班 姓名:____________
一 基础题
1.在研究硝酸钠的可溶性程度时,对不同的温度观测它在水中的溶解度,得观察数据:
温度 0 10 20 50 70
溶解度 66.7 76.0 85.0 112.3 128.0
则由此得到的回归直线的斜率是______________.
2.以下是收集到的新房屋的销售价格与房屋的大小的数据:
房屋大小() 115 110 80 135 105
销售价格(万元) 24.8 21.6 18.4 29.2 22
(1)画出散点图;
(2)求线性回归方程,并估计买的新房的费用.
二 提高题
3.以家庭为单位,某中商品年需求量与该商品价格之间的一组调查数据如下表:
价格(元) 5 2 2 2.3 2.5 2.6 2.8 3 3.3 3.5
需求量() 1 3.5 3 2.7 2.4 2.5 2 1.5 1.2 1.2
(1)画出散点图;
(2)求线性回归方程,并估计价格为元时该商品的需求量.
.精品资料。欢迎使用。 ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
例1
