(苏教版)溧水县第二高级中学数学教学案必修3:第21课时(随机现象和随机事件的概率)
文档属性
| 名称 | (苏教版)溧水县第二高级中学数学教学案必修3:第21课时(随机现象和随机事件的概率) |  | |
| 格式 | zip | ||
| 文件大小 | 28.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-06-22 12:34:24 | ||
图片预览

文档简介
总课题 概 率 总课时 第21课时
分课题 随机现象和随机事件的概率 分课时 第 1 课时
教学目标 了解必然事件,不可能事件及随机事件的意义;了解随机事件发生的不确定性及频率的稳定性,进一步了解概率的意义及概率与频率的区别;通过对概率的学习,使学生对对立统一的辩证规律有进一步认识.
重点难点 必然事件、不可能事件,随机事件的含义;根据统计定义计算概率的方法.
引入新课
1.观察下列现象:
(1)在标准大气压下,把水加热到100°C,沸腾; (2)导体通电,发热;
(3)实心铁块丢入水中,铁块浮起; (4)同性电荷,互相吸引; (5)买一张福到彩票,中奖; (6)掷一枚硬币,正面向上;
这些现象各有什么特点
2.(1)确定性现象与随机现象:
(2)试验与事件:
(3)事件的分类与事件的符号表示:
3.概率的定义及频率与概率的关系:
4.求事件的概率的基本方法:
注意:概率的取值范围是__________________________________.
例题剖析
例1 试判断下列事件是随机事件、必然事件还是不可能事件.
(1)我国东南沿海某地明年将次受到热带气旋的侵袭;
(2)若为实数,则;
(3)某人开车通过个路口都将遇到绿灯;
(4)抛一石块,石块下落;
(5)一个正六面体的六个面分别写有数字1,2,3,4,5,6,将它抛掷两次,向上的面的数字之和大于12.
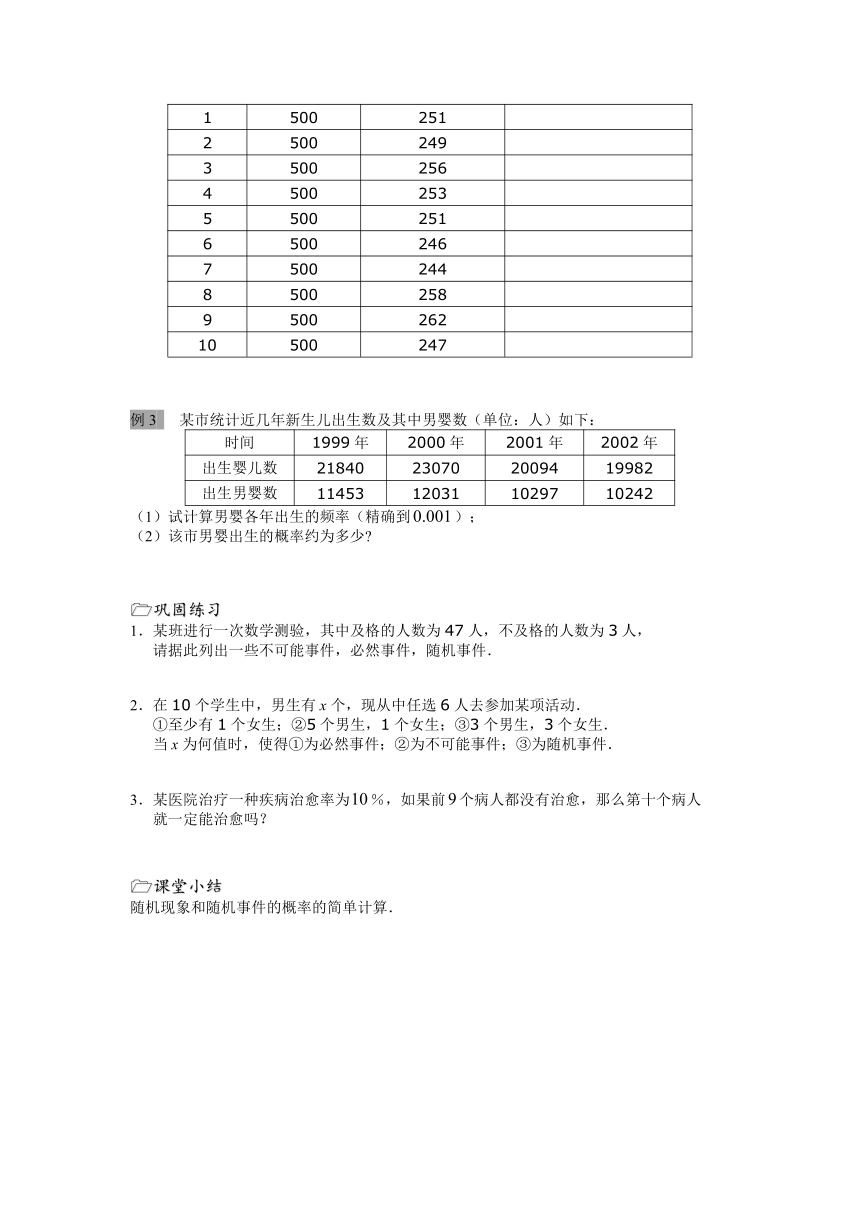
例2 下面表中列出10次抛掷硬币的试验结果,为每次试验抛掷硬币的次数,
为硬币正面向上的次数,计算每次试验中“正面向上”这一事件的频
率,并考查其概率.
试验序号 抛掷的次数 正面向上的次数 “正面向上”出现的频率
1 500 251
2 500 249
3 500 256
4 500 253
5 500 251
6 500 246
7 500 244
8 500 258
9 500 262
10 500 247
例3 某市统计近几年新生儿出生数及其中男婴数(单位:人)如下:
时间 1999年 2000年 2001年 2002年
出生婴儿数 21840 23070 20094 19982
出生男婴数 11453 12031 10297 10242
(1)试计算男婴各年出生的频率(精确到);
(2)该市男婴出生的概率约为多少
巩固练习
1.某班进行一次数学测验,其中及格的人数为47人,不及格的人数为3人,
请据此列出一些不可能事件,必然事件,随机事件.
2.在10个学生中,男生有x个,现从中任选6人去参加某项活动.
①至少有1个女生;②5个男生,1个女生;③3个男生,3个女生.
当x为何值时,使得①为必然事件;②为不可能事件;③为随机事件.
3.某医院治疗一种疾病治愈率为%,如果前个病人都没有治愈,那么第十个病人
就一定能治愈吗?
课堂小结
随机现象和随机事件的概率的简单计算.
课后训练
班级:高二( )班 姓名:____________
一 基础题
1.从15名学生中(其中男生10人,女生5人),任意选出6人的必然事件是( )
A.6人都是男生; B.至少有1人是女生;
C.6人都是女生; D.至少有1人是男生.
2.从1,2,3,…,10这10个数字中,任取3个数字,那么“这3个数字之和小于27”这一事件是( )
A.必然事件 B.不可能事件 C.随机事件 D.以上选项均不正确
3.给出下列事件:
①对非零向量,,若·,则⊥;
②直线()与函数的图象有两个不同的交点;
③若,,则;
④过空间任意三点,有且只有一个平面.
在以上事件中随机事的个数是( )
A.1 B.2 C.3 D.4
4.抛掷一枚硬币,连续5次正面向上,则有( )
A.抛掷一枚硬币,出现正面向上,概率为1;
B.第6次出现正面向上的概率大于;
C.第6次出现正面向上的概率等于;
D.第6次出现正面向上的概率小于.
5.设某种产品的合格率约为99%,估算10000件该产品中次品的件数可能是______件.
6.对某批种子的发芽情况统计,在统计的5000粒种子中共有4520粒发芽,
则“种子发芽”事件的频率为______________.
二 提高题
7.已知,,给出事件:.
(1)当为必然事件时,求的取值范围;
(2)当为不可能事件时,求的取值范围.
三 能力题
8.某射击运动负进行双向飞碟射击训练,各次训练的成绩记录如下:
射击次数 100 120 150 100 150 160 150
击中飞碟数 81 95 123 82 119 127 121
击中飞碟频率
(1)将各次记录击中飞碟的频率填入表中.
(2)这个运动员击中飞碟的概率约为多少
.精品资料。欢迎使用。 ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
分课题 随机现象和随机事件的概率 分课时 第 1 课时
教学目标 了解必然事件,不可能事件及随机事件的意义;了解随机事件发生的不确定性及频率的稳定性,进一步了解概率的意义及概率与频率的区别;通过对概率的学习,使学生对对立统一的辩证规律有进一步认识.
重点难点 必然事件、不可能事件,随机事件的含义;根据统计定义计算概率的方法.
引入新课
1.观察下列现象:
(1)在标准大气压下,把水加热到100°C,沸腾; (2)导体通电,发热;
(3)实心铁块丢入水中,铁块浮起; (4)同性电荷,互相吸引; (5)买一张福到彩票,中奖; (6)掷一枚硬币,正面向上;
这些现象各有什么特点
2.(1)确定性现象与随机现象:
(2)试验与事件:
(3)事件的分类与事件的符号表示:
3.概率的定义及频率与概率的关系:
4.求事件的概率的基本方法:
注意:概率的取值范围是__________________________________.
例题剖析
例1 试判断下列事件是随机事件、必然事件还是不可能事件.
(1)我国东南沿海某地明年将次受到热带气旋的侵袭;
(2)若为实数,则;
(3)某人开车通过个路口都将遇到绿灯;
(4)抛一石块,石块下落;
(5)一个正六面体的六个面分别写有数字1,2,3,4,5,6,将它抛掷两次,向上的面的数字之和大于12.
例2 下面表中列出10次抛掷硬币的试验结果,为每次试验抛掷硬币的次数,
为硬币正面向上的次数,计算每次试验中“正面向上”这一事件的频
率,并考查其概率.
试验序号 抛掷的次数 正面向上的次数 “正面向上”出现的频率
1 500 251
2 500 249
3 500 256
4 500 253
5 500 251
6 500 246
7 500 244
8 500 258
9 500 262
10 500 247
例3 某市统计近几年新生儿出生数及其中男婴数(单位:人)如下:
时间 1999年 2000年 2001年 2002年
出生婴儿数 21840 23070 20094 19982
出生男婴数 11453 12031 10297 10242
(1)试计算男婴各年出生的频率(精确到);
(2)该市男婴出生的概率约为多少
巩固练习
1.某班进行一次数学测验,其中及格的人数为47人,不及格的人数为3人,
请据此列出一些不可能事件,必然事件,随机事件.
2.在10个学生中,男生有x个,现从中任选6人去参加某项活动.
①至少有1个女生;②5个男生,1个女生;③3个男生,3个女生.
当x为何值时,使得①为必然事件;②为不可能事件;③为随机事件.
3.某医院治疗一种疾病治愈率为%,如果前个病人都没有治愈,那么第十个病人
就一定能治愈吗?
课堂小结
随机现象和随机事件的概率的简单计算.
课后训练
班级:高二( )班 姓名:____________
一 基础题
1.从15名学生中(其中男生10人,女生5人),任意选出6人的必然事件是( )
A.6人都是男生; B.至少有1人是女生;
C.6人都是女生; D.至少有1人是男生.
2.从1,2,3,…,10这10个数字中,任取3个数字,那么“这3个数字之和小于27”这一事件是( )
A.必然事件 B.不可能事件 C.随机事件 D.以上选项均不正确
3.给出下列事件:
①对非零向量,,若·,则⊥;
②直线()与函数的图象有两个不同的交点;
③若,,则;
④过空间任意三点,有且只有一个平面.
在以上事件中随机事的个数是( )
A.1 B.2 C.3 D.4
4.抛掷一枚硬币,连续5次正面向上,则有( )
A.抛掷一枚硬币,出现正面向上,概率为1;
B.第6次出现正面向上的概率大于;
C.第6次出现正面向上的概率等于;
D.第6次出现正面向上的概率小于.
5.设某种产品的合格率约为99%,估算10000件该产品中次品的件数可能是______件.
6.对某批种子的发芽情况统计,在统计的5000粒种子中共有4520粒发芽,
则“种子发芽”事件的频率为______________.
二 提高题
7.已知,,给出事件:.
(1)当为必然事件时,求的取值范围;
(2)当为不可能事件时,求的取值范围.
三 能力题
8.某射击运动负进行双向飞碟射击训练,各次训练的成绩记录如下:
射击次数 100 120 150 100 150 160 150
击中飞碟数 81 95 123 82 119 127 121
击中飞碟频率
(1)将各次记录击中飞碟的频率填入表中.
(2)这个运动员击中飞碟的概率约为多少
.精品资料。欢迎使用。 ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
