人教版八年级数学上册 第11章 三角形 11.2.2 三角形的外角 教案(导学案)(有答案)
文档属性
| 名称 | 人教版八年级数学上册 第11章 三角形 11.2.2 三角形的外角 教案(导学案)(有答案) | 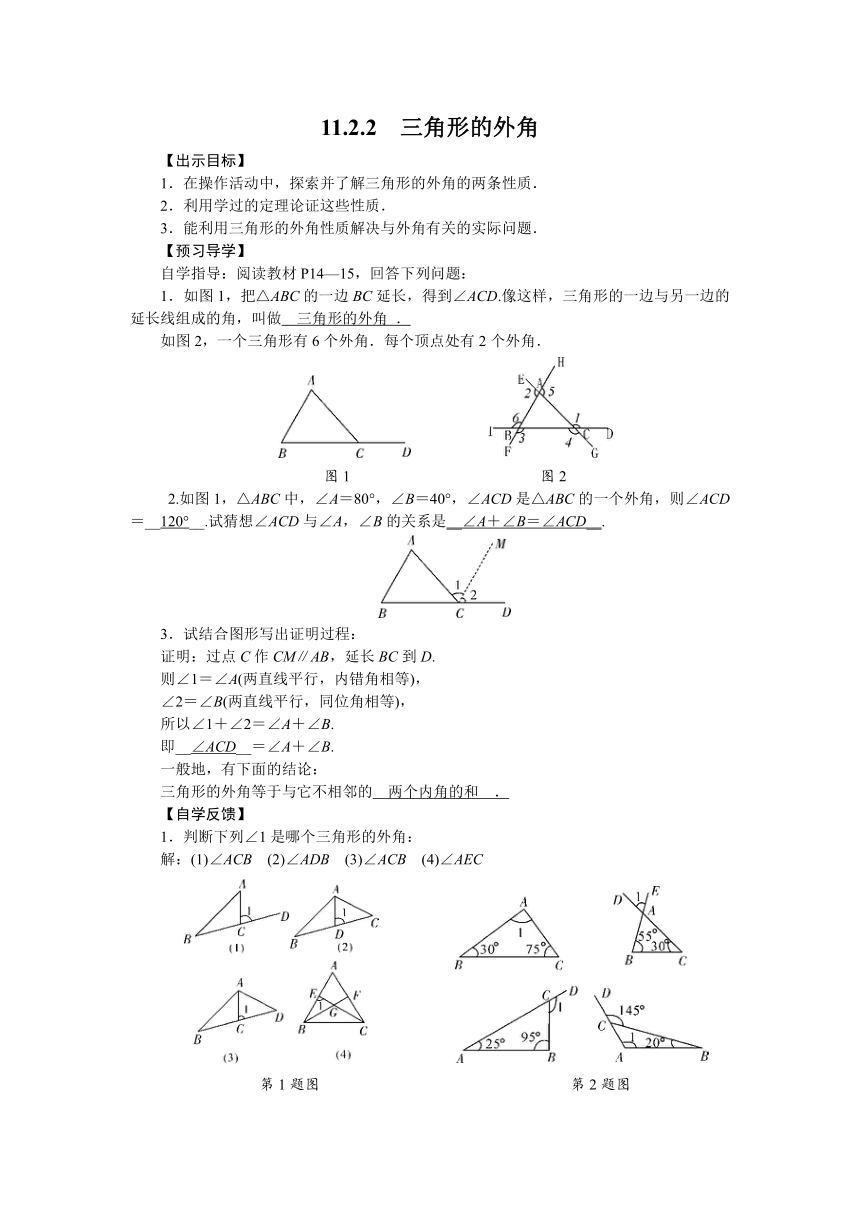 | |
| 格式 | docx | ||
| 文件大小 | 42.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-24 10:05:13 | ||
图片预览

文档简介
11.2.2 三角形的外角
【出示目标】
1.在操作活动中,探索并了解三角形的外角的两条性质.
2.利用学过的定理论证这些性质.
3.能利用三角形的外角性质解决与外角有关的实际问题.
【预习导学】
自学指导:阅读教材P14—15,回答下列问题:
1.如图1,把△ABC的一边BC延长,得到∠ACD.像这样,三角形的一边与另一边的延长线组成的角,叫做
三角形的外角
.
如图2,一个三角形有6个外角.每个顶点处有2个外角.
图1
图2
2.如图1,△ABC中,∠A=80°,∠B=40°,∠ACD是△ABC的一个外角,则∠ACD=__120°__.试猜想∠ACD与∠A,∠B的关系是__∠A+∠B=∠ACD__.
3.试结合图形写出证明过程:
证明:过点C作CM∥AB,延长BC到D.
则∠1=∠A(两直线平行,内错角相等),
∠2=∠B(两直线平行,同位角相等),
所以∠1+∠2=∠A+∠B.
即__∠ACD__=∠A+∠B.
一般地,有下面的结论:
三角形的外角等于与它不相邻的
两个内角的和
.
【自学反馈】
1.判断下列∠1是哪个三角形的外角:
解:(1)∠ACB (2)∠ADB (3)∠ACB (4)∠AEC
第1题图
第2题图
2.求下列各图中∠1的度数.
解:(1)75° (2)95° (3)170° (4)115°
【合作探究】
活动1 我思考,我发现(有勇气就会创造奇迹!)
1.定义:三角形__一边__与另一边的
延长线
组成的角,叫做三角形的外角.
第1题图
第2题图
2.画△ABC,你能画出所有的外角来吗?动手试一试,同时想一想,△ABC的外角共有几个呢?
解:6个.
活动2 三角形外角的性质
(1)看一看:图中哪些角是三角形的内角,哪些角是三角形的外角?
解:∠A、∠B、∠ACB是三角形的内角,∠ACD是三角形的外角.
(2)算一算:若∠A=70°,∠B=60°,你能求出∠ACD吗?如果能,∠ACD与∠A,∠B有什么关系?
解:∠ACD=130°,∠ACD=∠A+∠B.
(3)想一想:任何三角形的一个外角与它不相邻的两个内角是否都有这种关系?
解:有.
(4)证一证:证明你的猜想∠ACD=∠A+∠B.
解:因为∠A+∠B+∠ACB=180°,
∠ACD+∠ACB=180°,
所以∠ACD=∠A+∠B.
结论:
三角形的外角等于
与它不相邻的
两个内角之和.
活动3 三角形的外角和定理
1.如图,∠1+∠2+∠3=?
解:∠1+∠BAC=180°,
∠2+∠ABC=180°,
∠3+∠ACB=180°,
三个式子相加得到:
∠1+∠2+∠3+∠BAC+∠ABC+∠ACB=540°.
而∠BAC+∠ABC+∠ACB=180°,
所以∠1+∠2+∠3=360°.
2.结论:三角形的外角和是__360°__.
活动4 快乐之旅(闯关我们最棒!)
教师利用央视李勇主持的《非常6+1》的创意进行出题,提升学生学习兴趣.
1.求下列各图中∠1的度数.
∠1=90° ∠1=80°
∠1=95°
2.求下列各图中∠1和∠2的度数.
解:(1)∠1=60°,∠2=30° (2)∠1=50°,∠2=140°
3.已知三角形各外角的比为2∶3∶4,求则它的每个外角的度数.
解:设三个外角度数分别为:2x、3x、4x,由三角形外角和为360°得
2x+3x+4x=360°
解得x=40°
所以三个外角度数分别为80°,120°,160°.
4.如图,AB∥CD,∠A=40°,∠D=45°,求∠2和∠3.
解:∠2=40°,∠3=85°.
活动5 课堂小结
三角形外角的性质
1.三角形的外角等于与它不相邻的两个内角的和.
2.三角形的外角和是360°.
【随堂训练】
教学至此,敬请使用学案随堂训练部分
【出示目标】
1.在操作活动中,探索并了解三角形的外角的两条性质.
2.利用学过的定理论证这些性质.
3.能利用三角形的外角性质解决与外角有关的实际问题.
【预习导学】
自学指导:阅读教材P14—15,回答下列问题:
1.如图1,把△ABC的一边BC延长,得到∠ACD.像这样,三角形的一边与另一边的延长线组成的角,叫做
三角形的外角
.
如图2,一个三角形有6个外角.每个顶点处有2个外角.
图1
图2
2.如图1,△ABC中,∠A=80°,∠B=40°,∠ACD是△ABC的一个外角,则∠ACD=__120°__.试猜想∠ACD与∠A,∠B的关系是__∠A+∠B=∠ACD__.
3.试结合图形写出证明过程:
证明:过点C作CM∥AB,延长BC到D.
则∠1=∠A(两直线平行,内错角相等),
∠2=∠B(两直线平行,同位角相等),
所以∠1+∠2=∠A+∠B.
即__∠ACD__=∠A+∠B.
一般地,有下面的结论:
三角形的外角等于与它不相邻的
两个内角的和
.
【自学反馈】
1.判断下列∠1是哪个三角形的外角:
解:(1)∠ACB (2)∠ADB (3)∠ACB (4)∠AEC
第1题图
第2题图
2.求下列各图中∠1的度数.
解:(1)75° (2)95° (3)170° (4)115°
【合作探究】
活动1 我思考,我发现(有勇气就会创造奇迹!)
1.定义:三角形__一边__与另一边的
延长线
组成的角,叫做三角形的外角.
第1题图
第2题图
2.画△ABC,你能画出所有的外角来吗?动手试一试,同时想一想,△ABC的外角共有几个呢?
解:6个.
活动2 三角形外角的性质
(1)看一看:图中哪些角是三角形的内角,哪些角是三角形的外角?
解:∠A、∠B、∠ACB是三角形的内角,∠ACD是三角形的外角.
(2)算一算:若∠A=70°,∠B=60°,你能求出∠ACD吗?如果能,∠ACD与∠A,∠B有什么关系?
解:∠ACD=130°,∠ACD=∠A+∠B.
(3)想一想:任何三角形的一个外角与它不相邻的两个内角是否都有这种关系?
解:有.
(4)证一证:证明你的猜想∠ACD=∠A+∠B.
解:因为∠A+∠B+∠ACB=180°,
∠ACD+∠ACB=180°,
所以∠ACD=∠A+∠B.
结论:
三角形的外角等于
与它不相邻的
两个内角之和.
活动3 三角形的外角和定理
1.如图,∠1+∠2+∠3=?
解:∠1+∠BAC=180°,
∠2+∠ABC=180°,
∠3+∠ACB=180°,
三个式子相加得到:
∠1+∠2+∠3+∠BAC+∠ABC+∠ACB=540°.
而∠BAC+∠ABC+∠ACB=180°,
所以∠1+∠2+∠3=360°.
2.结论:三角形的外角和是__360°__.
活动4 快乐之旅(闯关我们最棒!)
教师利用央视李勇主持的《非常6+1》的创意进行出题,提升学生学习兴趣.
1.求下列各图中∠1的度数.
∠1=90° ∠1=80°
∠1=95°
2.求下列各图中∠1和∠2的度数.
解:(1)∠1=60°,∠2=30° (2)∠1=50°,∠2=140°
3.已知三角形各外角的比为2∶3∶4,求则它的每个外角的度数.
解:设三个外角度数分别为:2x、3x、4x,由三角形外角和为360°得
2x+3x+4x=360°
解得x=40°
所以三个外角度数分别为80°,120°,160°.
4.如图,AB∥CD,∠A=40°,∠D=45°,求∠2和∠3.
解:∠2=40°,∠3=85°.
活动5 课堂小结
三角形外角的性质
1.三角形的外角等于与它不相邻的两个内角的和.
2.三角形的外角和是360°.
【随堂训练】
教学至此,敬请使用学案随堂训练部分
