2021-2022学年人教版数学八年级上册13.2 用坐标表示轴对称 课件(共17张PPT)
文档属性
| 名称 | 2021-2022学年人教版数学八年级上册13.2 用坐标表示轴对称 课件(共17张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 735.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-07 00:00:00 | ||
图片预览





文档简介
(共17张PPT)
第十三章
轴对称
13.2
画轴对称图形
第2课时 用坐标表示轴对称
情景导入
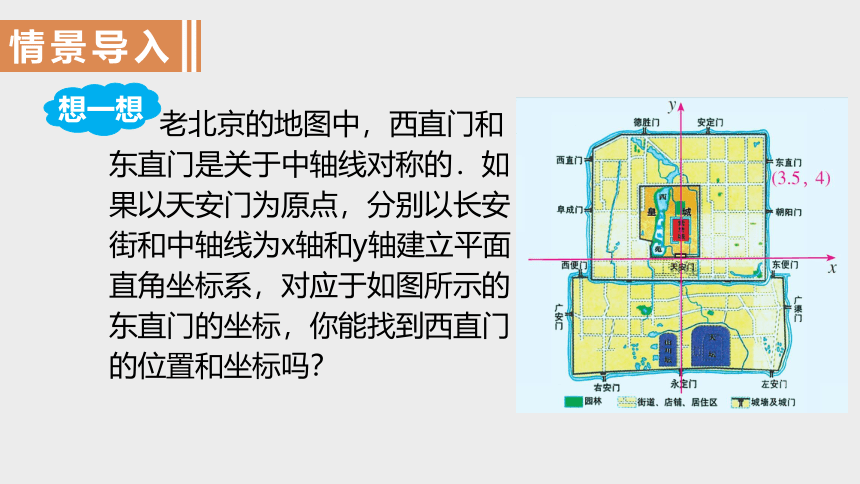
老北京的地图中,西直门和东直门是关于中轴线对称的.如果以天安门为原点,分别以长安街和中轴线为x轴和y轴建立平面直角坐标系,对应于如图所示的东直门的坐标,你能找到西直门的位置和坐标吗?
想一想
合作探究
知识板块一 关于x轴对称的点的坐标的特征
在下图的平面直角坐标系中,画出下列已知点及其关于坐标轴的对称点,并把它们的坐标填入表格中,看看每对对称点的坐标有怎样的规律,
再和同学讨论一下.
已知点
A(2,
-3)
B(-1,2)
C(-6,-5)
D(
,1)
E(4,0)
关于x轴的对
称点
A′
(
,)
B′
(
,
)
C′
(
,)
D′
(
,
)
E′
(
,
)
2
3
-1
-2
-6
5
-1
4
0
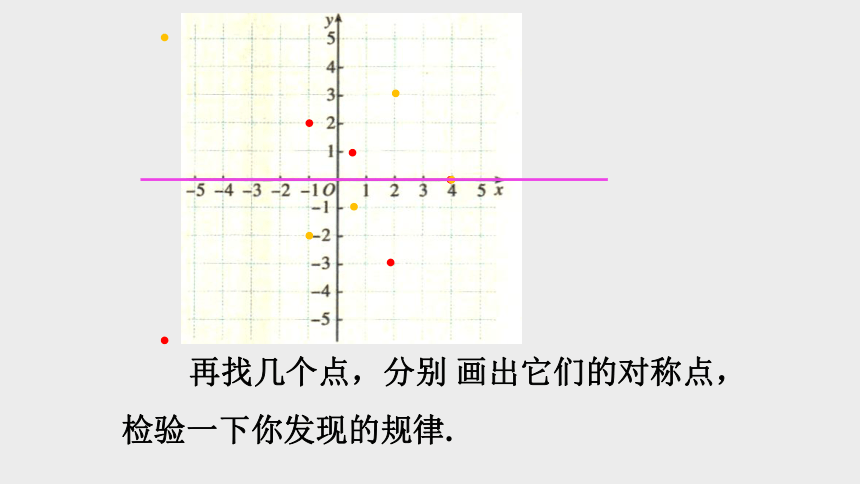
再找几个点,分别
画出它们的对称点,检验一下你发现的规律.
点(x
,
y)关于x轴对称的点的坐标为(x,
-y);
其特征为:横坐标相等,纵坐标互为相反数.
例1
已知点P1(a-1,
5
)和P2(2,
b-1)关于x轴对称,
则(a+b)2021的值为(
)
A.
0
B.
-1
C.
1
D.(-3)2016
分析:根据关于x轴对称的点的坐标特征可知a-1=2,
b
-1=-5,
解方程可得a
,
b的值,再代入求值即
可.
B
合作探究
知识板块二
关于y轴对称的点的坐标的特征
在下图的平面直角坐标系中,画出下列已知点及其关于坐标轴的对称点,并把它们的坐标填入表格中,看看每对对称点的坐标有怎样的规律,
再和同学讨论一下.
已知点
A(2,
-3)
B(-1,2)
C(-6,-5)
D(
,1)
E(4,0)
关于x轴的对
称点
A′
(
,)
B′
(
,
)
C′
(
,)
D′
(
,
)
E′
(
,
)
-2
-3
1
2
6
-5
-
1
-4
0
再找几个点,分别
画出它们的对称点,检验一下你发现的规律.
点(x
,
y)关于
y
轴对称的点的坐标为(-x,
y);
其特征为:横坐标互为相反数,纵坐标相等.
例2△ABC在平面直角坐标系中的位置如图所示.
(1)画出△ABC关于y轴对称的△A1B1C1;
(2)将△ABC向右平移6个单位长度,作出平移
后的△A2B2C2,并写出△A2B2C2各顶点的坐标;
(3)观察△A1B1C1和△A2B2C2,它们是否关于某条直线对称?若是,请在图上画出这条对称轴.
解:(1)△A1B1C1如图所示;
(2)∵△ABC向右平移6个单位长度,∴A,B,C三点的横坐标加6,纵坐标不变,作出△A2B2C2如图所示,A2(6,4),B2(4,2),C2(5,1);
(3)△A1B1C1和△A2B2C2关于图中直线l:x=3对称.
几何图形都可以看作由点组成.对于某些图形,只要画出图形中的一
些特殊点(如线段端点)的对称点,连接这些对称点,就可以得到原图形
的轴对称图形.
1.在平面直角坐标系中,点(-3,4)关于x轴对称的点是( )
A.(4,-3)
B.(-3,-4)
C.(3,4)
D.(3,-4)
当堂演练
B
当堂演练
2.如图,△ABC与△DEF关于y轴对称,
已知A(-4,6),B(-6,2),E(2,1),则点D的
坐标为( )
(-4,6)
(4,6)
(-2,1)
(6,2)
B
3.小莹和小博士下棋,小莹执圆子,小博士执方子.如图,棋盘中心方子的位置用(-1,0)表示,右下角方子的位置用(0,-1)表示.小莹将第4枚圆子放入棋盘后,所有棋子构成一个轴对称图形.她放的位置是(
)
A.(-2,1)
B.(-1,1)
C.(1,-2)
D.(-1,-2)
B
当堂演练
当堂演练
4.如图,以长方形ABCD的中心为原点建立平面直角坐标系,点A的坐标是(3,2),则点B的坐标是__________,点C的坐标是_____________,点D的坐标是_________.
(3,-2)
(-3,-2)
(-3,2)
课堂总结
1.点(x,y)关于x轴对称的点的坐标为
(x,-y).
2.点(x,y)关于y轴对称的点的坐标为(-x,y).
第十三章
轴对称
13.2
画轴对称图形
第2课时 用坐标表示轴对称
情景导入
老北京的地图中,西直门和东直门是关于中轴线对称的.如果以天安门为原点,分别以长安街和中轴线为x轴和y轴建立平面直角坐标系,对应于如图所示的东直门的坐标,你能找到西直门的位置和坐标吗?
想一想
合作探究
知识板块一 关于x轴对称的点的坐标的特征
在下图的平面直角坐标系中,画出下列已知点及其关于坐标轴的对称点,并把它们的坐标填入表格中,看看每对对称点的坐标有怎样的规律,
再和同学讨论一下.
已知点
A(2,
-3)
B(-1,2)
C(-6,-5)
D(
,1)
E(4,0)
关于x轴的对
称点
A′
(
,)
B′
(
,
)
C′
(
,)
D′
(
,
)
E′
(
,
)
2
3
-1
-2
-6
5
-1
4
0
再找几个点,分别
画出它们的对称点,检验一下你发现的规律.
点(x
,
y)关于x轴对称的点的坐标为(x,
-y);
其特征为:横坐标相等,纵坐标互为相反数.
例1
已知点P1(a-1,
5
)和P2(2,
b-1)关于x轴对称,
则(a+b)2021的值为(
)
A.
0
B.
-1
C.
1
D.(-3)2016
分析:根据关于x轴对称的点的坐标特征可知a-1=2,
b
-1=-5,
解方程可得a
,
b的值,再代入求值即
可.
B
合作探究
知识板块二
关于y轴对称的点的坐标的特征
在下图的平面直角坐标系中,画出下列已知点及其关于坐标轴的对称点,并把它们的坐标填入表格中,看看每对对称点的坐标有怎样的规律,
再和同学讨论一下.
已知点
A(2,
-3)
B(-1,2)
C(-6,-5)
D(
,1)
E(4,0)
关于x轴的对
称点
A′
(
,)
B′
(
,
)
C′
(
,)
D′
(
,
)
E′
(
,
)
-2
-3
1
2
6
-5
-
1
-4
0
再找几个点,分别
画出它们的对称点,检验一下你发现的规律.
点(x
,
y)关于
y
轴对称的点的坐标为(-x,
y);
其特征为:横坐标互为相反数,纵坐标相等.
例2△ABC在平面直角坐标系中的位置如图所示.
(1)画出△ABC关于y轴对称的△A1B1C1;
(2)将△ABC向右平移6个单位长度,作出平移
后的△A2B2C2,并写出△A2B2C2各顶点的坐标;
(3)观察△A1B1C1和△A2B2C2,它们是否关于某条直线对称?若是,请在图上画出这条对称轴.
解:(1)△A1B1C1如图所示;
(2)∵△ABC向右平移6个单位长度,∴A,B,C三点的横坐标加6,纵坐标不变,作出△A2B2C2如图所示,A2(6,4),B2(4,2),C2(5,1);
(3)△A1B1C1和△A2B2C2关于图中直线l:x=3对称.
几何图形都可以看作由点组成.对于某些图形,只要画出图形中的一
些特殊点(如线段端点)的对称点,连接这些对称点,就可以得到原图形
的轴对称图形.
1.在平面直角坐标系中,点(-3,4)关于x轴对称的点是( )
A.(4,-3)
B.(-3,-4)
C.(3,4)
D.(3,-4)
当堂演练
B
当堂演练
2.如图,△ABC与△DEF关于y轴对称,
已知A(-4,6),B(-6,2),E(2,1),则点D的
坐标为( )
(-4,6)
(4,6)
(-2,1)
(6,2)
B
3.小莹和小博士下棋,小莹执圆子,小博士执方子.如图,棋盘中心方子的位置用(-1,0)表示,右下角方子的位置用(0,-1)表示.小莹将第4枚圆子放入棋盘后,所有棋子构成一个轴对称图形.她放的位置是(
)
A.(-2,1)
B.(-1,1)
C.(1,-2)
D.(-1,-2)
B
当堂演练
当堂演练
4.如图,以长方形ABCD的中心为原点建立平面直角坐标系,点A的坐标是(3,2),则点B的坐标是__________,点C的坐标是_____________,点D的坐标是_________.
(3,-2)
(-3,-2)
(-3,2)
课堂总结
1.点(x,y)关于x轴对称的点的坐标为
(x,-y).
2.点(x,y)关于y轴对称的点的坐标为(-x,y).
