湘教版七上数学1.5.1有理数的乘法(1)课件(共27张PPT)
文档属性
| 名称 | 湘教版七上数学1.5.1有理数的乘法(1)课件(共27张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-07 20:46:47 | ||
图片预览







文档简介
(共27张PPT)
1.5.2
有理数的乘法(1)
湘教版
七年级上
教学目标
1.
理解有理数乘法的计算法则;
2.
学会计算有理数的乘法;
3.
通过观察、探索、归纳法则的过程,增强求知欲望;
4.
通过确定积的符号和绝对值,培养严谨的学习习惯.
列算式:
某地地面温度为0℃,若垂直高度每升高1千米,温度就
降低6℃,一架飞机正在离地面8.5千米的高空飞行,这
时飞机周围的温度是多少℃?
新知导入
以0℃为标准,通常低于0℃的温度记为负数,因此根据题意可列出算式:(-6)×8.5.
我们已经熟悉了非负数的乘法运算,例如
5×3=15,
那么如何计算像(-5)×3,3×(-5),(-5)×(-3)这样
的含有负因数的乘法呢?
新知导入
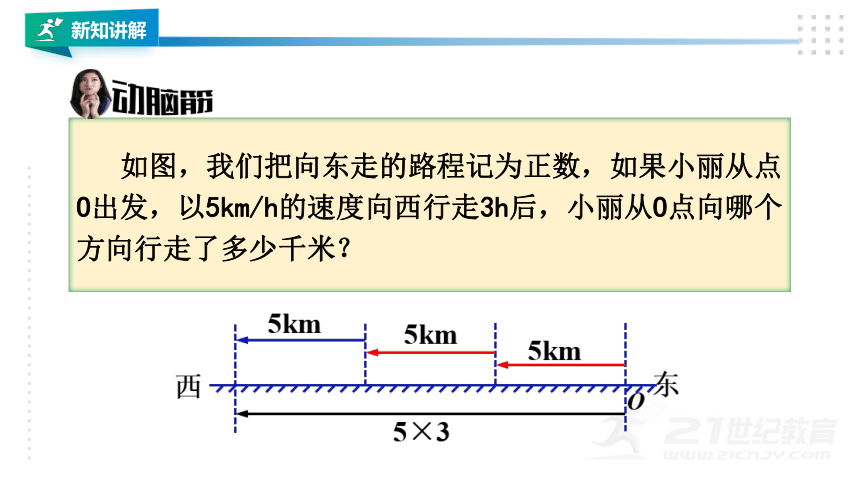
如图,我们把向东走的路程记为正数,如果小丽从点O出发,以5km/h的速度向西行走3h后,小丽从O点向哪个方向行走了多少千米?
新知讲解
新知讲解
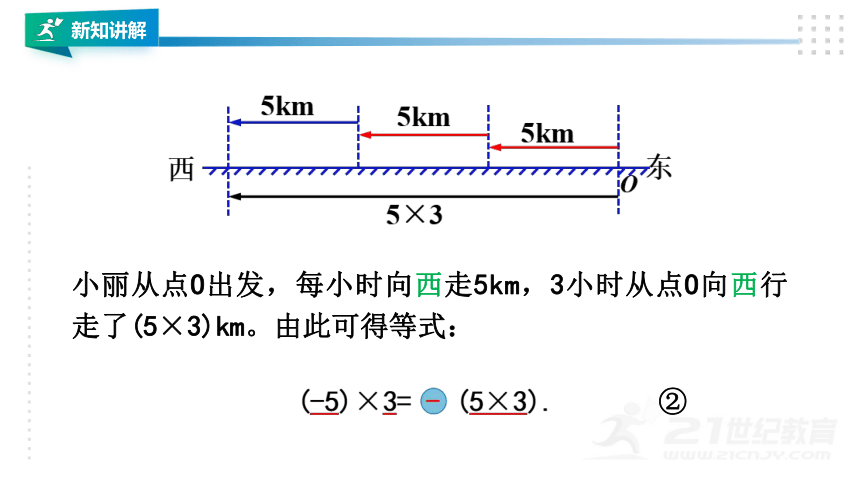
小丽从点O出发,每小时向西走5km,3小时从点O向西行走了(5×3)km。由此可得等式:
②
我们已经知道(-5)×3
=-(5×3),那么3×(-5),
(-5)×(-3)又怎样计算呢?
新知讲解
联想:非负数的乘法与加法是用分配律联系起来的,因此,当数扩充到有理数后,要规定有理数的乘法法则,当然也要求它满足分配律,以便把乘法与加法联系起来.
新知讲解
如果非负数的乘法满足分配律,那么就会有
3×(-5)+3×5=3×[(-5)+5]=3×0=0.
这表明3×(-5)与3×5互为相反数,于是有
从数的符号和绝对值两个方面,观察上面得到的
两个式子,你发现了什么?
新知讲解
新知讲解
从上面两个式子受到启发,一般规定:
异号两数相乘得负数,并把绝对值相乘.
新知讲解
根据类似的理由,规定:
任何数与0相乘,都得0.
新知讲解
类似地,我们有
(-5)×(-3)+(-5)×3
=(-5)×[(-3)+3]
=(-5)×0
=0.
这表明(-5)×(-3)与(-5)×3互为相反数.
新知讲解
因为
(-5)×3=-15,而-15的相反数是15,
所以
(-5)×(-3)=15.
即
(-5)×(-3)=15=5×3.
可以看出,(-5)×(-3)得正数,并把绝对值5与3相乘.
观察下面两个式子,你能得出什么结论?
新知讲解
5×3=15
(-5)×(-3)=5×3.
新知讲解
由此我们受到启发,于是规定:
同号两数相乘得正数,并把绝对值相乘.
例题讲解
例1
计算:
(2);
(3)
;
(1)
;
(4)
.
解:
(1)
(2)
(3)
(4)
.
例题讲解
例题讲解
有理数相乘,应先确定积的符号,再求绝对值的积.
提示:
巩固练习
1.
计算8×(-7)的结果是
(
)
A.
15
B.
-15
C.
56
D.
-56
D
解析:8×(-7)=-(8×7)=-56,故选D。
巩固练习
2.
计算(-4)×(-)的结果是
(
)
A.
-4
B.
-
C.
3
D.
-3
C
解析:
(-4)×(-)=4×
故选C。
巩固练习
3.
一个有理数和它的相反数的积
(
)
A.
一定是正数
B.
一定是负数
C.
一定是非负数
D.
一定是非正数
D
解析:若这个有理数为正数,则它的相反数为负数;若这个有理数为负数,则它的相反数为正数,根据有理数的乘法法则,则积为负数。而0的相反数是0,则积为0.所以一个有理数和它的相反数的积是负数或0,即为非正数。故选D。
巩固练习
4.
下列算式中,计算的结果是正数的是
(
)
A.
(-11)×(-11)
B.
(-10)+(-5)
C.
-16+20
D.
(-13)×7
A
解析:根据“同号两数相乘得正数”可知A符合题意,故选A.
课堂总结
异号两数相乘得负数,并把绝对值相乘;
同号两数相乘得正数,并把绝对值相乘;
任何数与0相乘,都得0.
2.
有理数相乘,应
1.
有理数的乘法法则有:
先确定积的符号,再求绝对值的积.
作业布置
1.填表:
因数
因数
积的符号
绝对值的积
积
-2
7
-1
0.3
-10
-
14
-14
+
-
3
-3
作业布置
2.
计算:
(1)
;
(2)
.
https://www.21cnjy.com/help/help_extract.php
1.5.2
有理数的乘法(1)
湘教版
七年级上
教学目标
1.
理解有理数乘法的计算法则;
2.
学会计算有理数的乘法;
3.
通过观察、探索、归纳法则的过程,增强求知欲望;
4.
通过确定积的符号和绝对值,培养严谨的学习习惯.
列算式:
某地地面温度为0℃,若垂直高度每升高1千米,温度就
降低6℃,一架飞机正在离地面8.5千米的高空飞行,这
时飞机周围的温度是多少℃?
新知导入
以0℃为标准,通常低于0℃的温度记为负数,因此根据题意可列出算式:(-6)×8.5.
我们已经熟悉了非负数的乘法运算,例如
5×3=15,
那么如何计算像(-5)×3,3×(-5),(-5)×(-3)这样
的含有负因数的乘法呢?
新知导入
如图,我们把向东走的路程记为正数,如果小丽从点O出发,以5km/h的速度向西行走3h后,小丽从O点向哪个方向行走了多少千米?
新知讲解
新知讲解
小丽从点O出发,每小时向西走5km,3小时从点O向西行走了(5×3)km。由此可得等式:
②
我们已经知道(-5)×3
=-(5×3),那么3×(-5),
(-5)×(-3)又怎样计算呢?
新知讲解
联想:非负数的乘法与加法是用分配律联系起来的,因此,当数扩充到有理数后,要规定有理数的乘法法则,当然也要求它满足分配律,以便把乘法与加法联系起来.
新知讲解
如果非负数的乘法满足分配律,那么就会有
3×(-5)+3×5=3×[(-5)+5]=3×0=0.
这表明3×(-5)与3×5互为相反数,于是有
从数的符号和绝对值两个方面,观察上面得到的
两个式子,你发现了什么?
新知讲解
新知讲解
从上面两个式子受到启发,一般规定:
异号两数相乘得负数,并把绝对值相乘.
新知讲解
根据类似的理由,规定:
任何数与0相乘,都得0.
新知讲解
类似地,我们有
(-5)×(-3)+(-5)×3
=(-5)×[(-3)+3]
=(-5)×0
=0.
这表明(-5)×(-3)与(-5)×3互为相反数.
新知讲解
因为
(-5)×3=-15,而-15的相反数是15,
所以
(-5)×(-3)=15.
即
(-5)×(-3)=15=5×3.
可以看出,(-5)×(-3)得正数,并把绝对值5与3相乘.
观察下面两个式子,你能得出什么结论?
新知讲解
5×3=15
(-5)×(-3)=5×3.
新知讲解
由此我们受到启发,于是规定:
同号两数相乘得正数,并把绝对值相乘.
例题讲解
例1
计算:
(2);
(3)
;
(1)
;
(4)
.
解:
(1)
(2)
(3)
(4)
.
例题讲解
例题讲解
有理数相乘,应先确定积的符号,再求绝对值的积.
提示:
巩固练习
1.
计算8×(-7)的结果是
(
)
A.
15
B.
-15
C.
56
D.
-56
D
解析:8×(-7)=-(8×7)=-56,故选D。
巩固练习
2.
计算(-4)×(-)的结果是
(
)
A.
-4
B.
-
C.
3
D.
-3
C
解析:
(-4)×(-)=4×
故选C。
巩固练习
3.
一个有理数和它的相反数的积
(
)
A.
一定是正数
B.
一定是负数
C.
一定是非负数
D.
一定是非正数
D
解析:若这个有理数为正数,则它的相反数为负数;若这个有理数为负数,则它的相反数为正数,根据有理数的乘法法则,则积为负数。而0的相反数是0,则积为0.所以一个有理数和它的相反数的积是负数或0,即为非正数。故选D。
巩固练习
4.
下列算式中,计算的结果是正数的是
(
)
A.
(-11)×(-11)
B.
(-10)+(-5)
C.
-16+20
D.
(-13)×7
A
解析:根据“同号两数相乘得正数”可知A符合题意,故选A.
课堂总结
异号两数相乘得负数,并把绝对值相乘;
同号两数相乘得正数,并把绝对值相乘;
任何数与0相乘,都得0.
2.
有理数相乘,应
1.
有理数的乘法法则有:
先确定积的符号,再求绝对值的积.
作业布置
1.填表:
因数
因数
积的符号
绝对值的积
积
-2
7
-1
0.3
-10
-
14
-14
+
-
3
-3
作业布置
2.
计算:
(1)
;
(2)
.
https://www.21cnjy.com/help/help_extract.php
同课章节目录
