2021—2022学年人教版数学七年级上册1.4.1.1有理数的乘法课件 (30张PPT)
文档属性
| 名称 | 2021—2022学年人教版数学七年级上册1.4.1.1有理数的乘法课件 (30张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 489.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-06 00:00:00 | ||
图片预览









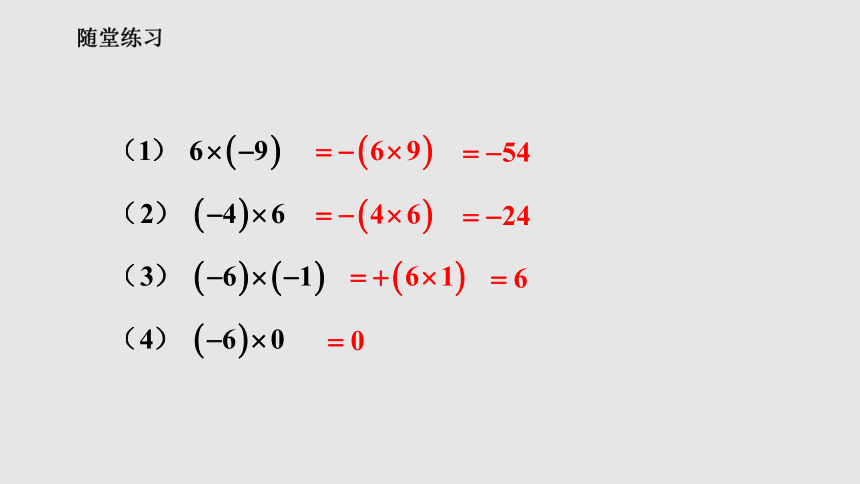
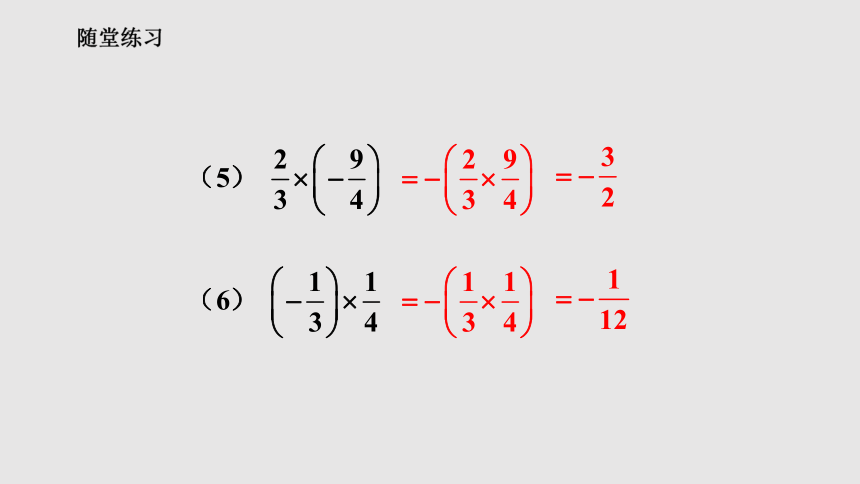
文档简介
(共30张PPT)
有理数的乘法
有理数的乘法
有理数的乘法
学习目标
1、理解有理数的乘法法则;
2、倒数的相关概念;
3、能利用有理数的乘法法则进行简单的有理数乘法运算.
应用有理数的乘法法则正确的进行有理数乘法计算。
重点
有理数的乘法法则中符号变化的理解及积的符号的确定。
难点
重难点
创设情境
甲水库的水位每天升高
3
cm,乙水库的水位每天下降
3
cm,4
天后甲、
乙水库水位的总变化量各是多少?
如果用正号表示水位上升,用负号表示水位下降,那么
4
天后
乙水库的水位变化量为:
甲水库的水位变化量为:
创设情境
一个因数互为相反数,结果也互为相反数
议一议
有理数乘法法则
两数相乘,同号得正,异号得负,并把绝对值相乘.
任何数同0相乘,仍得0.
乘法法则
同号两数相乘
得正
绝对值相乘
所以:
乘法法则
例如:
异号两数相乘
得负
绝对值相乘
所以:
有理数相乘,可以先确定积的符号,再确定积的绝对值。
乘法法则
例1
计算:
要得到一个数的相反数,只要将它乘
随堂练习
随堂练习
倒数
一般的,在有理数中仍然有:
乘积是1的两个数互为倒数。
我们说和互为倒数.
其中,
根据倒数的定义,我们可知:
互为倒数的两数乘积为
1
.
常用此性质来简化有理数运算。
倒数
练习
(1)的倒数是____________;
思考:0有倒数吗?
特殊地,0没有倒数!
(2)的倒数是____________;
1倒数是1,-1的倒数是-1.
写出下列各数的倒数:
互为相反数的两个数,其倒数也是互为相反数。
随堂练习
例2
用正负数表示气温的变化量,上升为正,下降为负。登山队攀登一座山峰,每登高1km气温的变化量为-6℃,攀登3km后,气温有什么变化?
解:
答:气温下降18℃
商店降价销售某种商品,每件降5元,售出60件后,与按原价销售相同数量的商品相比,销售额有什么变化?
解:
答:销售额减少300元.
随堂练习
观察下列各式,它们的积是正的还是负的?
多个有理数相乘,可以把它们按照顺序依次相乘。
思考
议一议
几个有理数相乘,因数都不为
0
时,积的符号怎样确定?
有一个因数为
0
时,积是多少?
负因数个数为奇数时积为负,负因数个数为偶数时积为正。
例2
先确定积的符号,再计算积的绝对值。
你能看出下式的结果吗?如果能,请说明理由。
几个数相乘,如果其中有一个因数为0,那么积就等于0.
思考
口算:
随堂练习
计算:
随堂练习
计算:
随堂练习
基础巩固
1.若四个互不相等的整数的积为6,那么这四个整数的和是(
)
A.-1或5
B.1或-5
C.-5或5
D.-1或1
D
2.已知三个有理数m、n、p,满足m+n=0,nA.负数
B.零
C.正数
D.非负数
A
3.已处x,y为有理数,现规定一种新运算※,满足。
(1)求的值;
(2)求
(3)探索的关系。
(1)
(2)
基础巩固
3.已处x,y为有理数,现规定一种新运算※,满足。
(1)求的值;
(2)求
(3)探索的关系。
(3)
所以
基础巩固
有理数的乘法法则
知识
考点
有理数的乘法运算
倒数的相关概念
课堂总结
有理数的乘法法则
有理数的乘法
有理数的乘法
有理数的乘法
学习目标
1、理解有理数的乘法法则;
2、倒数的相关概念;
3、能利用有理数的乘法法则进行简单的有理数乘法运算.
应用有理数的乘法法则正确的进行有理数乘法计算。
重点
有理数的乘法法则中符号变化的理解及积的符号的确定。
难点
重难点
创设情境
甲水库的水位每天升高
3
cm,乙水库的水位每天下降
3
cm,4
天后甲、
乙水库水位的总变化量各是多少?
如果用正号表示水位上升,用负号表示水位下降,那么
4
天后
乙水库的水位变化量为:
甲水库的水位变化量为:
创设情境
一个因数互为相反数,结果也互为相反数
议一议
有理数乘法法则
两数相乘,同号得正,异号得负,并把绝对值相乘.
任何数同0相乘,仍得0.
乘法法则
同号两数相乘
得正
绝对值相乘
所以:
乘法法则
例如:
异号两数相乘
得负
绝对值相乘
所以:
有理数相乘,可以先确定积的符号,再确定积的绝对值。
乘法法则
例1
计算:
要得到一个数的相反数,只要将它乘
随堂练习
随堂练习
倒数
一般的,在有理数中仍然有:
乘积是1的两个数互为倒数。
我们说和互为倒数.
其中,
根据倒数的定义,我们可知:
互为倒数的两数乘积为
1
.
常用此性质来简化有理数运算。
倒数
练习
(1)的倒数是____________;
思考:0有倒数吗?
特殊地,0没有倒数!
(2)的倒数是____________;
1倒数是1,-1的倒数是-1.
写出下列各数的倒数:
互为相反数的两个数,其倒数也是互为相反数。
随堂练习
例2
用正负数表示气温的变化量,上升为正,下降为负。登山队攀登一座山峰,每登高1km气温的变化量为-6℃,攀登3km后,气温有什么变化?
解:
答:气温下降18℃
商店降价销售某种商品,每件降5元,售出60件后,与按原价销售相同数量的商品相比,销售额有什么变化?
解:
答:销售额减少300元.
随堂练习
观察下列各式,它们的积是正的还是负的?
多个有理数相乘,可以把它们按照顺序依次相乘。
思考
议一议
几个有理数相乘,因数都不为
0
时,积的符号怎样确定?
有一个因数为
0
时,积是多少?
负因数个数为奇数时积为负,负因数个数为偶数时积为正。
例2
先确定积的符号,再计算积的绝对值。
你能看出下式的结果吗?如果能,请说明理由。
几个数相乘,如果其中有一个因数为0,那么积就等于0.
思考
口算:
随堂练习
计算:
随堂练习
计算:
随堂练习
基础巩固
1.若四个互不相等的整数的积为6,那么这四个整数的和是(
)
A.-1或5
B.1或-5
C.-5或5
D.-1或1
D
2.已知三个有理数m、n、p,满足m+n=0,n
B.零
C.正数
D.非负数
A
3.已处x,y为有理数,现规定一种新运算※,满足。
(1)求的值;
(2)求
(3)探索的关系。
(1)
(2)
基础巩固
3.已处x,y为有理数,现规定一种新运算※,满足。
(1)求的值;
(2)求
(3)探索的关系。
(3)
所以
基础巩固
有理数的乘法法则
知识
考点
有理数的乘法运算
倒数的相关概念
课堂总结
有理数的乘法法则
