江西省南昌市2022届高三上学期摸底考试数学(理)试题(Word版,含答案)
文档属性
| 名称 | 江西省南昌市2022届高三上学期摸底考试数学(理)试题(Word版,含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 650.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-06 14:21:19 | ||
图片预览



文档简介
南昌市2022届高三摸底测试卷
理科数学
本试卷共4页,23小题,满分150分0考试时间120分钟.
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号填涂在答题卡上,并在相应位置贴好条形码.
2.作答选择题时,选出每小题答案后,用2B铅笔把答题卡上对应题目的答案信息涂黑、如需改动,用橡皮擦干净后,再选涂其它答案.
3.非选择题必须用黑色水笔作答,答案必须写在答题卡各题目指定区域内相应位置上;如需改动,先划掉原来答案,然后再写上新答案,不准使用铅笔和涂改液.不按以上要求作答无效.
4.考生必须保证答题卡整洁.考试结束后,将试卷和答题卡一并交回.
一.选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.集合的元素个数为(
)
A.3
B.4
C.5
D.6
2.若z为纯虚数,且,则(
)
A.i
B.-i
C.2i
D.-2i
3.为数列的前n项和,若,,则(
)
A.
B.
C.10
D.
4.设F为抛物线焦点,直线,点A为C上任意一点,过点A作于P,则(
)
A.3
B.4
C.2.
D.不能确定
5.直线,,则“”是“”的(
)
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
6.已知向量,,则(
)
A.
B.
C.
D.5
7.某市出台两套出租车计价方案,方案一:2公里以内收费8元(起步价),超过2公里的部分每公里收费3元,不足1公里按1公里计算;方案二:3公里以内收费12元(起步价),超过3公里不超过10公里的部分每公里收费2.5元,超过10公里的部分每公里收费3.5元,不足1公里按1公里计算.以下说法正确的是(
)
A.方案二比方案一更优惠
B.乘客甲打车行驶4公里,他应该选择方案二
C.乘客乙打车行驶12公里,他应该选择方案二
D.乘客丙打车行驶16公里,他应该选择方案二
8.已知,且,则的值为(
)
A.
B.
C.
D.
9.函数的图像大致为(
)
A.B.C.D.
10.已知数列满足,则的前20项和(
)
A.
B.
C.
D.
11.已知双曲线的左、右焦点分别为、,过的直线l与C的左、右支分别相交于M、N两点,若,,则双曲线的离心率为(
)
A.
B.
C.2
D.
12.已知函数,若,若点不可能在曲线C上,则曲线C的方程可以是(
)
A.
B.
C.
D.
二.填空题:本题共4小题,每小题5分,共20分.
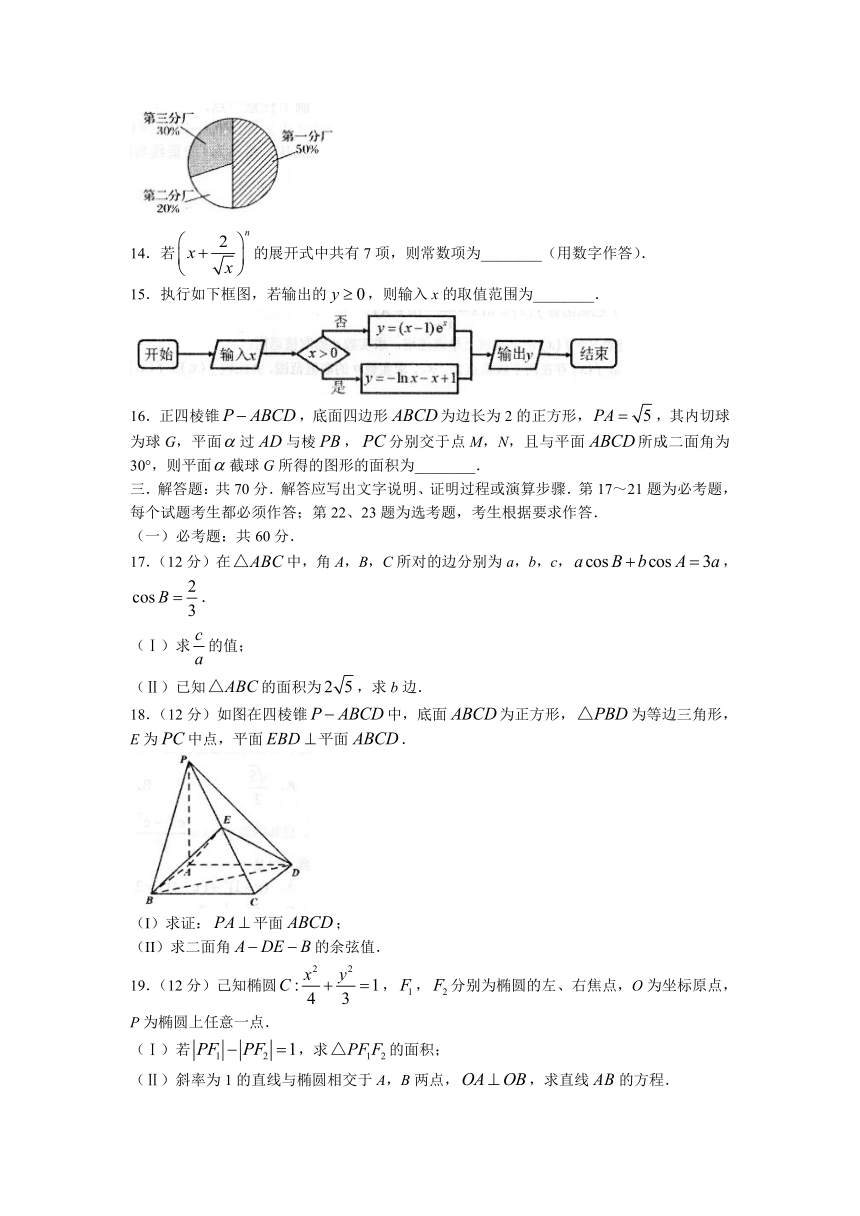
13.某企业三个分厂生产同一种电子产品,三个分厂的产量分布如图所示.现在用分层抽样方法从三个分厂生产的产品中共抽取100件进行使用寿命的测试,测试结果为第一、二、三分厂取出的产品的平均使用寿命分别为1020小时、980小时、1030小时,估计这个企业生产的产品的平均使用寿命为________小时.
14.若的展开式中共有7项,则常数项为________(用数字作答).
15.执行如下框图,若输出的,则输入x的取值范围为________.
16.正四棱锥,底面四边形为边长为2的正方形,,其内切球为球G,平面过与棱,分别交于点M,N,且与平面所成二面角为30°,则平面截球G所得的图形的面积为________.
三.解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试题考生都必须作答;第22、23题为选考题,考生根据要求作答.
(一)必考题:共60分.
17.(12分)在中,角A,B,C所对的边分别为a,b,c,,.
(Ⅰ)求的值;
(Ⅱ)已知的面积为,求b边.
18.(12分)如图在四棱锥中,底面为正方形,为等边三角形,E为中点,平面平面.
(I)求证:平面;
(II)求二面角的余弦值.
19.(12分)己知椭圆,,分别为椭圆的左、右焦点,O为坐标原点,P为椭圆上任意一点.
(Ⅰ)若,求的面积;
(Ⅱ)斜率为1的直线与椭圆相交于A,B两点,,求直线的方程.
20.(12分)已知函数.
(Ⅰ)若函数在定义域上单调递增,求实数a的取值范围;
(Ⅱ)若函数存在两个极值点,,求实数a的取值范围,并比较与的大小.
21.(12分)甲、乙、丙、丁、戊五位同学参加一次节日活动,他们都有机会抽取奖券.墙上挂着两串奖券袋(如图),A,B,C,D,E五个袋子分别装有价值100,80,120,200,90(单位:元)的奖券,抽取方法是这样的:每个同学只能从其中一串的最下端取一个袋子,得到其中奖券,直到礼物取完为止.甲先取,然后乙、丙、丁、戊依次取,若两串都有礼物袋,则每个人等可能选择一串取.
(Ⅰ)求丙取得的礼物券为80元的概率;
(Ⅱ)记丁取得的礼物券为X元,求X的分布列及其数学期望.
(二)选考题:共10分.请考生在第22、23题中任选一题作答,如果多做,则按所做的第一题计分.
22.(10分)选修4-4:坐标系与参数方程
在平面直角坐标系中,直线l的参数方程为(t为参数),以坐标原点O为极点,x轴正半轴为极轴,建立极坐标系,曲线C的极坐标方程为.
(Ⅰ)求直线l的普通方程和曲线C的直角坐标方程;
(Ⅱ)设,直线l与曲线C的交点为M,N,求.
23.(10分)选修4-5:不等式选讲
已知函数.
(Ⅰ)当时,求不等式的解集;
(Ⅱ)若对任意,都有恒成立,求实数a的取值范围.
2022届高三摸底测试卷
理科数学参考答案及评分标准
一、选择题:本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
C
C
C
A
A
A
C
C
B
D
B
C
二.填空题:本大题共4小题,每小题5分,满分20分.
13.1015
14.240
15.
16.
三.解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第17题-21题为必考题,每个试题考生都必须作答.第22题、23题为选考题,考生根据要求作答.
17.【解析】(Ⅰ)由正弦定理,(其中R为外接圆的半径),
所以,,,
代入已知条件可得:,
2分
所以,即,
4分
,故.
6分
(Ⅱ)由已知可得,
所以的面积为,
故,解得,.
9分
所以,即.
12分
18.【解析】(Ⅰ)连接交于点O,连接、,
因为为等边三角形,所以,
因为底面为正方形,所以,
因为,所以平面,
3分
又平面,所以,
因为平面平面,平面平面,
所以平面,
因为E为中点,所以,则平面.
5分
(Ⅱ)如图,以为x轴,为y轴,为z轴,
建立空间直角坐标系,设,则,
所以,,,,
则,,,
因为平面平面,
所以平面的法向量为,
7分
设平面的法向量为,则,
所以,所以,
9分
所以,
11分
所以二面角的余弦值为.
12分
19.【解析】(Ⅰ)由题意,解得,,
2分
又,所以,
即,
4分
所以;
5分
(Ⅱ)直线斜率为1,设直线方程,,,
由,消元得,得
7分
又,知,即
9分
而
所以,,得,满足,
所以直线的方程或.
12分
20.【解析】(Ⅰ)由得
2分
由题在恒成立,即在恒成立
而,所以;
5分
(Ⅱ)
由题意知,,是方程在内的两个不同实数解,
令,
注意到,其对称轴为直线,
故只需,解得,
即实数a的取值范围为;
8分
由,是方程的两根,得
,,
因此
,
10分
又,所以,
即得证.
12分
21.【解析】(Ⅰ)由题意知,列举如下:
2分
所以丙取得的礼物券为80元的概率
;
(Ⅱ)如下图,
所以X的可能取值为100,80,200,90,
又因为;
;
;
;
所以分布列为:
8分(每个概率1分)
X
80
90
100
200
P
所以.
22.【解析】(Ⅰ)直线l的参数方程为(t为参数),
转换为普通方程为
2分
曲线C的极坐标方程为,
根据转换为直角坐标方程为.
5分
(Ⅱ)易知直线l的参数方程标准形式为代入到中,
得到;设M,N所对应的参数分别为,,
则,,
8分
所以.
10分
23.【解析】(Ⅰ)因为,所以,
当时,,所以;
当时,,所以,
综上不等式的解集为.
5分
(II)因为,
8分
当时,在单调递增;当时,;
所以函数的最小值是a,所以.
10分
理科数学
本试卷共4页,23小题,满分150分0考试时间120分钟.
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号填涂在答题卡上,并在相应位置贴好条形码.
2.作答选择题时,选出每小题答案后,用2B铅笔把答题卡上对应题目的答案信息涂黑、如需改动,用橡皮擦干净后,再选涂其它答案.
3.非选择题必须用黑色水笔作答,答案必须写在答题卡各题目指定区域内相应位置上;如需改动,先划掉原来答案,然后再写上新答案,不准使用铅笔和涂改液.不按以上要求作答无效.
4.考生必须保证答题卡整洁.考试结束后,将试卷和答题卡一并交回.
一.选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.集合的元素个数为(
)
A.3
B.4
C.5
D.6
2.若z为纯虚数,且,则(
)
A.i
B.-i
C.2i
D.-2i
3.为数列的前n项和,若,,则(
)
A.
B.
C.10
D.
4.设F为抛物线焦点,直线,点A为C上任意一点,过点A作于P,则(
)
A.3
B.4
C.2.
D.不能确定
5.直线,,则“”是“”的(
)
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
6.已知向量,,则(
)
A.
B.
C.
D.5
7.某市出台两套出租车计价方案,方案一:2公里以内收费8元(起步价),超过2公里的部分每公里收费3元,不足1公里按1公里计算;方案二:3公里以内收费12元(起步价),超过3公里不超过10公里的部分每公里收费2.5元,超过10公里的部分每公里收费3.5元,不足1公里按1公里计算.以下说法正确的是(
)
A.方案二比方案一更优惠
B.乘客甲打车行驶4公里,他应该选择方案二
C.乘客乙打车行驶12公里,他应该选择方案二
D.乘客丙打车行驶16公里,他应该选择方案二
8.已知,且,则的值为(
)
A.
B.
C.
D.
9.函数的图像大致为(
)
A.B.C.D.
10.已知数列满足,则的前20项和(
)
A.
B.
C.
D.
11.已知双曲线的左、右焦点分别为、,过的直线l与C的左、右支分别相交于M、N两点,若,,则双曲线的离心率为(
)
A.
B.
C.2
D.
12.已知函数,若,若点不可能在曲线C上,则曲线C的方程可以是(
)
A.
B.
C.
D.
二.填空题:本题共4小题,每小题5分,共20分.
13.某企业三个分厂生产同一种电子产品,三个分厂的产量分布如图所示.现在用分层抽样方法从三个分厂生产的产品中共抽取100件进行使用寿命的测试,测试结果为第一、二、三分厂取出的产品的平均使用寿命分别为1020小时、980小时、1030小时,估计这个企业生产的产品的平均使用寿命为________小时.
14.若的展开式中共有7项,则常数项为________(用数字作答).
15.执行如下框图,若输出的,则输入x的取值范围为________.
16.正四棱锥,底面四边形为边长为2的正方形,,其内切球为球G,平面过与棱,分别交于点M,N,且与平面所成二面角为30°,则平面截球G所得的图形的面积为________.
三.解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试题考生都必须作答;第22、23题为选考题,考生根据要求作答.
(一)必考题:共60分.
17.(12分)在中,角A,B,C所对的边分别为a,b,c,,.
(Ⅰ)求的值;
(Ⅱ)已知的面积为,求b边.
18.(12分)如图在四棱锥中,底面为正方形,为等边三角形,E为中点,平面平面.
(I)求证:平面;
(II)求二面角的余弦值.
19.(12分)己知椭圆,,分别为椭圆的左、右焦点,O为坐标原点,P为椭圆上任意一点.
(Ⅰ)若,求的面积;
(Ⅱ)斜率为1的直线与椭圆相交于A,B两点,,求直线的方程.
20.(12分)已知函数.
(Ⅰ)若函数在定义域上单调递增,求实数a的取值范围;
(Ⅱ)若函数存在两个极值点,,求实数a的取值范围,并比较与的大小.
21.(12分)甲、乙、丙、丁、戊五位同学参加一次节日活动,他们都有机会抽取奖券.墙上挂着两串奖券袋(如图),A,B,C,D,E五个袋子分别装有价值100,80,120,200,90(单位:元)的奖券,抽取方法是这样的:每个同学只能从其中一串的最下端取一个袋子,得到其中奖券,直到礼物取完为止.甲先取,然后乙、丙、丁、戊依次取,若两串都有礼物袋,则每个人等可能选择一串取.
(Ⅰ)求丙取得的礼物券为80元的概率;
(Ⅱ)记丁取得的礼物券为X元,求X的分布列及其数学期望.
(二)选考题:共10分.请考生在第22、23题中任选一题作答,如果多做,则按所做的第一题计分.
22.(10分)选修4-4:坐标系与参数方程
在平面直角坐标系中,直线l的参数方程为(t为参数),以坐标原点O为极点,x轴正半轴为极轴,建立极坐标系,曲线C的极坐标方程为.
(Ⅰ)求直线l的普通方程和曲线C的直角坐标方程;
(Ⅱ)设,直线l与曲线C的交点为M,N,求.
23.(10分)选修4-5:不等式选讲
已知函数.
(Ⅰ)当时,求不等式的解集;
(Ⅱ)若对任意,都有恒成立,求实数a的取值范围.
2022届高三摸底测试卷
理科数学参考答案及评分标准
一、选择题:本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
C
C
C
A
A
A
C
C
B
D
B
C
二.填空题:本大题共4小题,每小题5分,满分20分.
13.1015
14.240
15.
16.
三.解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第17题-21题为必考题,每个试题考生都必须作答.第22题、23题为选考题,考生根据要求作答.
17.【解析】(Ⅰ)由正弦定理,(其中R为外接圆的半径),
所以,,,
代入已知条件可得:,
2分
所以,即,
4分
,故.
6分
(Ⅱ)由已知可得,
所以的面积为,
故,解得,.
9分
所以,即.
12分
18.【解析】(Ⅰ)连接交于点O,连接、,
因为为等边三角形,所以,
因为底面为正方形,所以,
因为,所以平面,
3分
又平面,所以,
因为平面平面,平面平面,
所以平面,
因为E为中点,所以,则平面.
5分
(Ⅱ)如图,以为x轴,为y轴,为z轴,
建立空间直角坐标系,设,则,
所以,,,,
则,,,
因为平面平面,
所以平面的法向量为,
7分
设平面的法向量为,则,
所以,所以,
9分
所以,
11分
所以二面角的余弦值为.
12分
19.【解析】(Ⅰ)由题意,解得,,
2分
又,所以,
即,
4分
所以;
5分
(Ⅱ)直线斜率为1,设直线方程,,,
由,消元得,得
7分
又,知,即
9分
而
所以,,得,满足,
所以直线的方程或.
12分
20.【解析】(Ⅰ)由得
2分
由题在恒成立,即在恒成立
而,所以;
5分
(Ⅱ)
由题意知,,是方程在内的两个不同实数解,
令,
注意到,其对称轴为直线,
故只需,解得,
即实数a的取值范围为;
8分
由,是方程的两根,得
,,
因此
,
10分
又,所以,
即得证.
12分
21.【解析】(Ⅰ)由题意知,列举如下:
2分
所以丙取得的礼物券为80元的概率
;
(Ⅱ)如下图,
所以X的可能取值为100,80,200,90,
又因为;
;
;
;
所以分布列为:
8分(每个概率1分)
X
80
90
100
200
P
所以.
22.【解析】(Ⅰ)直线l的参数方程为(t为参数),
转换为普通方程为
2分
曲线C的极坐标方程为,
根据转换为直角坐标方程为.
5分
(Ⅱ)易知直线l的参数方程标准形式为代入到中,
得到;设M,N所对应的参数分别为,,
则,,
8分
所以.
10分
23.【解析】(Ⅰ)因为,所以,
当时,,所以;
当时,,所以,
综上不等式的解集为.
5分
(II)因为,
8分
当时,在单调递增;当时,;
所以函数的最小值是a,所以.
10分
同课章节目录
