2020-2021学年高二数学人教B版(2019)选择性必修第二册综合检测卷 (Word含答案解析)
文档属性
| 名称 | 2020-2021学年高二数学人教B版(2019)选择性必修第二册综合检测卷 (Word含答案解析) |  | |
| 格式 | doc | ||
| 文件大小 | 729.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-08 21:45:14 | ||
图片预览




文档简介
第二册 综合检测卷
一、选择题(共13道,每一道4分,共52分:其中1—10题为单项选择题,每题只有一个正确答案;第11—13题为多项选择题,每题至少有两个正确答案,答案不全得2分,有错误选项得0分.)
1.记者要为5名志愿者和他们帮助的2位老人拍照,要求排成一排,2位老人相邻但不排在两端,不同的排法共有(
).
A.1
440种
B.960种
C.720种
D.480种
2.的展开式中x2y3的系数是(
).
A.-20
B.-5
C.5
D.20
3.已知方程ay=b2x2+c,其中a,b,c{-3,-2,0,1,2,3},且a,b,c互不相同,则在所有这些方程所表示的曲线中,不同的抛物线共有(
).
A.60条
B.62条
C.71条
D.80条
4.设复数z=(x-1)+yi(x,yR),若|z|≤1,则y≥x的概率为(
).
A.
B.
C.
D.
5.将序号1,2,3,4,5的5张参观券全部分给4人,每人至少一张,如果分给同一人的2张参观券连号,那么不同的分法种数为(
).
A.128
B.64
C.96
D.80
6.从个位数与十位数之和为奇数的两位数中任取一个,其个位数为的概率是(
).
A.
B.
C.
D.
7.已知某批零件的长度误差(单位:毫米)服从正态分布N(0,32),从中随机取一件,其长度误差落在区间(3,6)内的概率为(
).
(附:若随机变量ξ服从正态分布N(μ,σ2),则P(μ-σ<ξ<μ+σ)=68.26%,P(μ-2σ<ξ<μ+2σ)=95.44%.)
A.4.56%
B.13.59%
C.27.18%
D.31.74%
8.设样本数据x1,x2,…,x10的均值和方差分别为1和4,若yi=xi+a(a为非零常数,
i=1,2,…,10),则y1,y2,…,y10的均值和方差分别为(
).
A.1+a,4
B.1+a,4+a
C.1,4
D.1,4+a
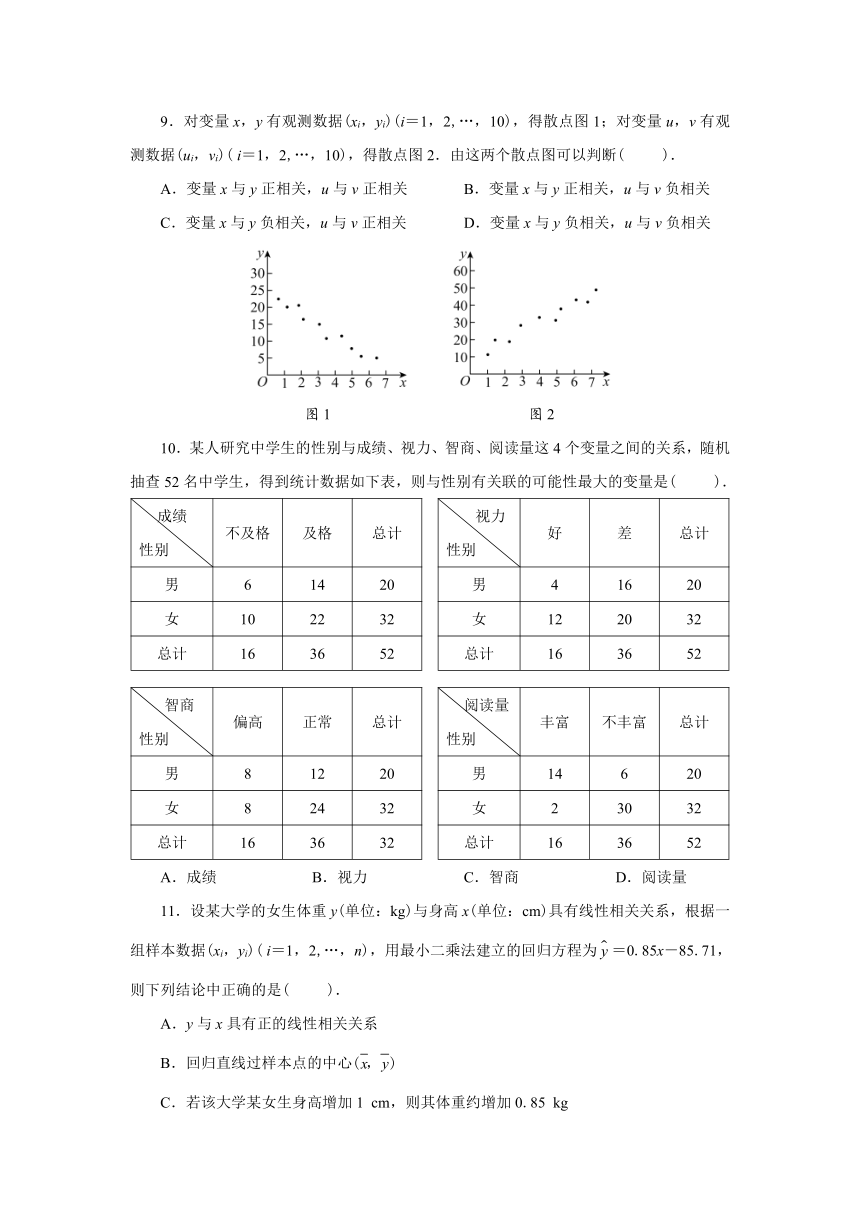
9.对变量x,y有观测数据(xi,yi)(i=1,2,…,10),得散点图1;对变量u,v有观测数据(ui,vi)(
i=1,2,…,10),得散点图2.由这两个散点图可以判断(
).
A.变量x与y正相关,u与v正相关
B.变量x与y正相关,u与v负相关
C.变量x与y负相关,u与v正相关
D.变量x与y负相关,u与v负相关
图1
图2
10.某人研究中学生的性别与成绩、视力、智商、阅读量这4个变量之间的关系,随机抽查52名中学生,得到统计数据如下表,则与性别有关联的可能性最大的变量是(
).
成绩性别
不及格
及格
总计
男
6
14
20
女
10
22
32
总计
16
36
52
视力性别好差总计男41620女122032总计163652
智商性别偏高正常总计男81220女82432总计163632
阅读量性别丰富不丰富总计男14620女23032总计163652
A.成绩
B.视力
C.智商
D.阅读量
11.设某大学的女生体重y(单位:kg)与身高x(单位:cm)具有线性相关关系,根据一组样本数据(xi,yi)(
i=1,2,…,n),用最小二乘法建立的回归方程为=0.85x-85.71,则下列结论中正确的是(
).
A.y与x具有正的线性相关关系
B.回归直线过样本点的中心
C.若该大学某女生身高增加1
cm,则其体重约增加0.85
kg
D.若该大学某女生身高为170
cm,则可近似认为其体重为58.79
kg
12.下列命题为真命题的是(
).
A.若一个球的半径缩小到原来的,则其体积缩小到原来的
B.若两组数据的平均数相等,则它们的标准差也相等
C.直线x+y+1=0与圆x2+y2=相切
D.“a≤0”是“函数f(x)=|(ax-1)x|在区间(0,+∞)内单调递增”的充分必要条件
13.设M,N为两个随机事件,则下列命题为真命题的是(
).
A.若P(M)=,P(N)=,P(MN)=,则M,N为相互独立事件
B.若P()=,P(N)=,P(MN)=,则M,N为相互独立事件
C.若P(M)=,P()=,P(MN)=,则M,N为相互独立事件
D.若M,N为互斥事件,P(M)=,P(N)=,P(MN)=
二、填空题(共5道,每一道4分,共20分.)
14.我国古代数学名著《九章算术》有“米谷粒分”题:粮仓开仓收粮,有人送来米1
534石,验得米内夹谷,抽样取米一把,数得254粒内夹谷28粒,则这批米内夹谷约为__________.
15.甲、乙、丙三位同学被问到是否去过A,B,C三个城市时:
甲说:我去过的城市比乙多,但没去过B城市;
乙说:我没去过C城市;
丙说:我们三个去过同一城市.
由此可判断乙去过的城市为__________.
16.若的展开式中x3项的系数为20,则a2+b2的最小值__________.
17.在区间[-3,3]上随机取一个数x,使得|x+1|-|x-2|≥1成立的概率为__________.
18.将一枚均匀的硬币投掷6次,则正面出现的次数比反面出现的次数多的概率为__________.
三、解答题(共5道,共78分.)
19.(15分)已知箱中装有4个白球和5个黑球,且规定:取出一个白球得2分,取出一个黑球得1分.现从该箱中任取(无放回,且每球取到的机会均等)3个球,记随机变量X为取出此3球所得分数之和.
(1)求X的分布列;
(2)求X的数学期望E(X).
20.(15分)某高校共有15
000人,其中男生10
500人,女生4
500人,为调查该校学生每周平均体育运动时间的情况,采用分层抽样的方法,收集300位学生每周平均体育运动时间的样本数据(单位:小时).
(1)应收集多少位女生样本数据?
(2)根据这300个样本数据,得到学生每周平均体育运动时间的频率分布直方图(如图所示),其中样本数据分组区间为:[0,2],(2,4],(4,6],(6,8],(8,10],(10,12].估计该校学生每周平均体育运动时间超过4个小时的概率.
(3)在样本数据中,有60位女生的每周平均体育运动时间超过4个小时.请完成每周平均体育运动时间与性别的列联表,并判断是否有95%的把握认为“该校学生的每周平均体育运动时间与性别有关”.
附:
P(χ2≥)
0.1
0.05
0.01
0.005
2.706
3.841
6.635
7.879
21.(15分)一款击鼓小游戏的规则如下:每盘游戏都需要击鼓三次,每次击鼓要么出现一次音乐,要么不出现音乐;每盘游戏击鼓三次后,出现一次音乐获得10分,出现两次音乐获得20分,出现三次音乐获得100分,没有出现音乐则扣除200分(即获得-200分).设每次击鼓出现音乐的概率为,且各次击鼓出现音乐相互独立.
(1)设每盘游戏获得的分数为X,求X的分布列;
(2)玩三盘游戏,至少有一盘出现音乐的概率是多少?
(3)玩过这款游戏的许多人都发现,若干盘游戏后,与最初的分数相比,分数没有增加反而减少了.请运用概率统计的相关知识分析分数减少的原因.
22.(15分)设袋子中装有a个红球,b个黄球,c个蓝球,且规定:取出一个红球得1分,取出一个黄球得2分,取出一个蓝球得3分.
(1)当a=3,b=2,c=1时,从该袋子中任取(有放回,且每球取到的机会均等)2个球,记随机变量ζ为取出此2球所得分数之和,求ζ的分布列;
(2)从该袋子中任取(每球取到的机会均等)1个球,记随机变量η为取出此球所得分数.若E(η)=,D(η)=,求a∶b∶c.
23.(18分)某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费x(单位:千元)对年销售量y(单位:t)和年利润z(单位:千元)的影响,对近8年的年宣传费xi和年销售量yi(i=1,2,···,8)数据作了初步处理,得到下面的散点图及一些统计量的值.
46.6
56.3
6.8
289.8
1.6
1
469
108.8
表中,.
(1)根据散点图判断,y=a+bx与y=c+d哪一个适宜作为年销售量y关于年宣传费x的回归方程类型?(给出判断即可,不必说明理由)
(2)根据(1)的判断结果及表中数据,建立y关于x的回归方程;
(3)已知这种产品的年利率z与x、y的关系为z=0.2y-x.根据(2)的结果回答下列问题:
(i)年宣传费x=49时,年销售量及年利润的预报值是多少?
(ii)年宣传费x为何值时,年利率的预报值最大?
附:对于一组数据(u1,v1),(u2,v2),…,(un,vn),其回归线的斜率和截距的最小二乘估计分别为:
,.
参考答案
一、选择题.
1.B.
解析:因为2位老人相邻,所以可以把他们当成一个整体,有种情况;然后排5个自愿者,有种排法;最后把看成整体的老人插在志愿者形成的4个空隙中,有种排法.由分步计数原理可知共有种排法.
2.A.
解析:根据二项式定理可得第n+1项展开式为,则n=2时,
,所以x2y3的系数为-20.
3.B.
解析:由已知有a≠0,b≠0,因此a,b的取法有种,c的取法有种,即可形成抛物线的条数为.当b=±2时,b2的值相同,重复的抛物线有条;同理,当b=±3时,也有重复的抛物线9条.所以,不同的抛物线有80-9-9=62条.
4.B.
解析:由已知有,即(x-1)2+y2≤1,如图可求得A(1,1),B(1,0),阴影面积等于.
因此所求概率是.
5.C.
解析:先确定哪两张是分给同一人的,有4种方法;再将参观券分下去,有种方法.由分步计数原理可知有4=4×24=96种分法.
6.D.
解析:一共有90个两位数,满足条件的两位数有45个.当个位数为0时,十位数为1,3,5,7,9共5个,因此所求概率为.
7.B.
解析:用表示ξ零件的长度,根据正态分布的性质得:
P(3<ξ<6)=[P(-6<ξ<6)-P(-3<ξ<3)]
=[95.44%-68.26%]=13.59%.
8.A.
解析:由题意有
.
方差
9.C.
解析:观察散点图,利用正相关和负相关的概念即可判断.
10.D.
解析:根据公式,将数据分别代入计算可得.
11.ABCD.
解析:由回归方程可知,y随x的增大而增大,所以y与x具有正的线性相关关系,
A选项正确;由最小二乘法建立回归方程的过程,可知,因此回归直线必过样本中心,B选项正确;由回归方程可知身高每增加1
cm,体重约增加0.85
kg,C选项正确;若某女生身高为170
cm,根据回归方程可近似认为体重为58.79
kg,D选项正确.
12.ACD.
解析:由球的体积公式可知A选项正确;两组数据的平均数相等,方差可能不相等,B选项错误;直线x+y+1=0到圆x2+y2=的距离为,因此直线与圆相切,C选项正确;f(x)=|(ax-1)x|的图象恒过原点,当a=0时,f(x)=|x|在区间(0,+∞)内单调递增;当a<0时,函数g(x)=(ax-1)x的对称轴x=<0,则f(x)=|(ax-1)x|在区间(0,+∞)内单调递增;当a>0时,g(x)=(ax-1)x的对称轴x=>0,由图象可知,在区间(0,+∞)内不是单调递增的,D选项正确.
13.ABD.
解析:P(M)=,P(N)=,若M,N为相互独立事件,则由相互独立事件的乘法公式可知P(MN)=,可知A、B选项正确;C选项中,由P(M)=,P()=,若M,N为相互独立事件,则P(MN)=,该选项错误;D选项中,若M,N为互斥事件,且P(M)=,P(N)=,则P(MN)=+=,该选项正确.
二、填空题
14.169石.
解析:依题意,这批米内夹谷约为×1
534=169石.
15.A.
解析:由丙说可知,乙至少去过A,B,C中的一个城市,由甲说可知,甲去过A,C且比乙去过的城市多,故乙只去过一个城市,且没去过C城市,故乙只去过A城市.
16.2.
解析:展开式的通项为,令12-3r=3,得r=3,所以由=20得ab=1,从而a2+b2≥2ab=2,当且仅当a=b时,a2+b2的最小值为2.
17..
解析:y=|x+1|-|x-2|=解得|x+1|-|x-2|≥1的解集为
[1,+∞).而在[-3,3]上满足不等式的x取值范围为[1,3],故所求概率为.
18..
解析:硬币投掷6次,有三类情况,①正面次数比反面次数多;②反面次数比正面次数多;③正面次数和反面次数一样多,其概率为,①②的概率显然相同,故①的概率为.
三、解答题
19.解:(1)由题意可知,X可取3,4,5,6,且
P(X=3)==,P(X=4)==,P(X=5)==,P(X=6)==.
因此X的分布列为:
X
3
4
5
6
P
(2)由(1)知,
E(X)=3·P(X=3)+3·P(X=3)+4·P(X=4)+5·P(X=5)+6·P(X=6)=.
20.解:(1)×4
500=90.所以应该收集90位女生的样本数据.
(2)由频率分布直方图得
P(X>4)=2(0.15+0.125+0.075+0.025)=0.75.
所以该校学生每周平均体育运动时间超过4小时的概率的估计值为0.75.
(3)每周平均运动时间与性别列联表如下:
运动超过4小时
运动不超过4小时
合计
男生
165
45
210
女生
60
30
90
合计
225
75
300
因此
χ2==≈4.762>3.841.
所以,有95%的把握认为“该校学生的每周平均体育运动时间与性别有关”.
21.解:(1)P(X=-200)==;
P(X=10)==;
P(X=20)==;
P(X=100)==;
所以X的分布列为:
X
-200
10
20
100
P
(2)由(1)可知,玩一盘游戏,没有音乐出现的概率为P0=;则玩三盘游戏,至少有一盘出现音乐的概率为P=;
(3)由(1)可得,E(X)=(-200)·+10·+20·+100·=-,每盘所得分数的期望为负数,所以玩得越多,所得分数越少的可能性越大.
22.解:由题意可知ζ=2,3,4,5,6,所以
P(ζ=2)=×=,P(ζ=3)=2××=,P(ζ=4)=×+2××=,P(ζ=5)=2××=,P(ζ=6)=×=;
所以ζ的分布列为:
ζ
2
3
4
5
6
P
(2)由题意知η的分布列为:
η
1
2
3
P
所以E(η)=++=,
D(η)=,
化简得解得a=3c,b=2c,故a∶b∶c=3∶2∶1.
23.解:(1)由散点图及所给图象可知,y=c+适合作为年销售y关于年宣传费用x的回归方程类型;
(2)令w=,建立y关于w的线性回归方程,由于
==68,
所以=563-68×6.8=100.6.y关于w的线性回归方程为=100.6+68w.
(3)(i)由(2)知,当x=49时,年销售量y的预报值
=100.6+=576.6,
=576.6×0.2-49=66.32.
(ii)根据(2)的结果知,年利润z的预报值
=0.2(100.6+)-x=-x++20.12,
所以当==6.8,即x=46.24时,取得最大值.
故宣传费用为46.24千元时,年利润的预报值最大.
一、选择题(共13道,每一道4分,共52分:其中1—10题为单项选择题,每题只有一个正确答案;第11—13题为多项选择题,每题至少有两个正确答案,答案不全得2分,有错误选项得0分.)
1.记者要为5名志愿者和他们帮助的2位老人拍照,要求排成一排,2位老人相邻但不排在两端,不同的排法共有(
).
A.1
440种
B.960种
C.720种
D.480种
2.的展开式中x2y3的系数是(
).
A.-20
B.-5
C.5
D.20
3.已知方程ay=b2x2+c,其中a,b,c{-3,-2,0,1,2,3},且a,b,c互不相同,则在所有这些方程所表示的曲线中,不同的抛物线共有(
).
A.60条
B.62条
C.71条
D.80条
4.设复数z=(x-1)+yi(x,yR),若|z|≤1,则y≥x的概率为(
).
A.
B.
C.
D.
5.将序号1,2,3,4,5的5张参观券全部分给4人,每人至少一张,如果分给同一人的2张参观券连号,那么不同的分法种数为(
).
A.128
B.64
C.96
D.80
6.从个位数与十位数之和为奇数的两位数中任取一个,其个位数为的概率是(
).
A.
B.
C.
D.
7.已知某批零件的长度误差(单位:毫米)服从正态分布N(0,32),从中随机取一件,其长度误差落在区间(3,6)内的概率为(
).
(附:若随机变量ξ服从正态分布N(μ,σ2),则P(μ-σ<ξ<μ+σ)=68.26%,P(μ-2σ<ξ<μ+2σ)=95.44%.)
A.4.56%
B.13.59%
C.27.18%
D.31.74%
8.设样本数据x1,x2,…,x10的均值和方差分别为1和4,若yi=xi+a(a为非零常数,
i=1,2,…,10),则y1,y2,…,y10的均值和方差分别为(
).
A.1+a,4
B.1+a,4+a
C.1,4
D.1,4+a
9.对变量x,y有观测数据(xi,yi)(i=1,2,…,10),得散点图1;对变量u,v有观测数据(ui,vi)(
i=1,2,…,10),得散点图2.由这两个散点图可以判断(
).
A.变量x与y正相关,u与v正相关
B.变量x与y正相关,u与v负相关
C.变量x与y负相关,u与v正相关
D.变量x与y负相关,u与v负相关
图1
图2
10.某人研究中学生的性别与成绩、视力、智商、阅读量这4个变量之间的关系,随机抽查52名中学生,得到统计数据如下表,则与性别有关联的可能性最大的变量是(
).
成绩性别
不及格
及格
总计
男
6
14
20
女
10
22
32
总计
16
36
52
视力性别好差总计男41620女122032总计163652
智商性别偏高正常总计男81220女82432总计163632
阅读量性别丰富不丰富总计男14620女23032总计163652
A.成绩
B.视力
C.智商
D.阅读量
11.设某大学的女生体重y(单位:kg)与身高x(单位:cm)具有线性相关关系,根据一组样本数据(xi,yi)(
i=1,2,…,n),用最小二乘法建立的回归方程为=0.85x-85.71,则下列结论中正确的是(
).
A.y与x具有正的线性相关关系
B.回归直线过样本点的中心
C.若该大学某女生身高增加1
cm,则其体重约增加0.85
kg
D.若该大学某女生身高为170
cm,则可近似认为其体重为58.79
kg
12.下列命题为真命题的是(
).
A.若一个球的半径缩小到原来的,则其体积缩小到原来的
B.若两组数据的平均数相等,则它们的标准差也相等
C.直线x+y+1=0与圆x2+y2=相切
D.“a≤0”是“函数f(x)=|(ax-1)x|在区间(0,+∞)内单调递增”的充分必要条件
13.设M,N为两个随机事件,则下列命题为真命题的是(
).
A.若P(M)=,P(N)=,P(MN)=,则M,N为相互独立事件
B.若P()=,P(N)=,P(MN)=,则M,N为相互独立事件
C.若P(M)=,P()=,P(MN)=,则M,N为相互独立事件
D.若M,N为互斥事件,P(M)=,P(N)=,P(MN)=
二、填空题(共5道,每一道4分,共20分.)
14.我国古代数学名著《九章算术》有“米谷粒分”题:粮仓开仓收粮,有人送来米1
534石,验得米内夹谷,抽样取米一把,数得254粒内夹谷28粒,则这批米内夹谷约为__________.
15.甲、乙、丙三位同学被问到是否去过A,B,C三个城市时:
甲说:我去过的城市比乙多,但没去过B城市;
乙说:我没去过C城市;
丙说:我们三个去过同一城市.
由此可判断乙去过的城市为__________.
16.若的展开式中x3项的系数为20,则a2+b2的最小值__________.
17.在区间[-3,3]上随机取一个数x,使得|x+1|-|x-2|≥1成立的概率为__________.
18.将一枚均匀的硬币投掷6次,则正面出现的次数比反面出现的次数多的概率为__________.
三、解答题(共5道,共78分.)
19.(15分)已知箱中装有4个白球和5个黑球,且规定:取出一个白球得2分,取出一个黑球得1分.现从该箱中任取(无放回,且每球取到的机会均等)3个球,记随机变量X为取出此3球所得分数之和.
(1)求X的分布列;
(2)求X的数学期望E(X).
20.(15分)某高校共有15
000人,其中男生10
500人,女生4
500人,为调查该校学生每周平均体育运动时间的情况,采用分层抽样的方法,收集300位学生每周平均体育运动时间的样本数据(单位:小时).
(1)应收集多少位女生样本数据?
(2)根据这300个样本数据,得到学生每周平均体育运动时间的频率分布直方图(如图所示),其中样本数据分组区间为:[0,2],(2,4],(4,6],(6,8],(8,10],(10,12].估计该校学生每周平均体育运动时间超过4个小时的概率.
(3)在样本数据中,有60位女生的每周平均体育运动时间超过4个小时.请完成每周平均体育运动时间与性别的列联表,并判断是否有95%的把握认为“该校学生的每周平均体育运动时间与性别有关”.
附:
P(χ2≥)
0.1
0.05
0.01
0.005
2.706
3.841
6.635
7.879
21.(15分)一款击鼓小游戏的规则如下:每盘游戏都需要击鼓三次,每次击鼓要么出现一次音乐,要么不出现音乐;每盘游戏击鼓三次后,出现一次音乐获得10分,出现两次音乐获得20分,出现三次音乐获得100分,没有出现音乐则扣除200分(即获得-200分).设每次击鼓出现音乐的概率为,且各次击鼓出现音乐相互独立.
(1)设每盘游戏获得的分数为X,求X的分布列;
(2)玩三盘游戏,至少有一盘出现音乐的概率是多少?
(3)玩过这款游戏的许多人都发现,若干盘游戏后,与最初的分数相比,分数没有增加反而减少了.请运用概率统计的相关知识分析分数减少的原因.
22.(15分)设袋子中装有a个红球,b个黄球,c个蓝球,且规定:取出一个红球得1分,取出一个黄球得2分,取出一个蓝球得3分.
(1)当a=3,b=2,c=1时,从该袋子中任取(有放回,且每球取到的机会均等)2个球,记随机变量ζ为取出此2球所得分数之和,求ζ的分布列;
(2)从该袋子中任取(每球取到的机会均等)1个球,记随机变量η为取出此球所得分数.若E(η)=,D(η)=,求a∶b∶c.
23.(18分)某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费x(单位:千元)对年销售量y(单位:t)和年利润z(单位:千元)的影响,对近8年的年宣传费xi和年销售量yi(i=1,2,···,8)数据作了初步处理,得到下面的散点图及一些统计量的值.
46.6
56.3
6.8
289.8
1.6
1
469
108.8
表中,.
(1)根据散点图判断,y=a+bx与y=c+d哪一个适宜作为年销售量y关于年宣传费x的回归方程类型?(给出判断即可,不必说明理由)
(2)根据(1)的判断结果及表中数据,建立y关于x的回归方程;
(3)已知这种产品的年利率z与x、y的关系为z=0.2y-x.根据(2)的结果回答下列问题:
(i)年宣传费x=49时,年销售量及年利润的预报值是多少?
(ii)年宣传费x为何值时,年利率的预报值最大?
附:对于一组数据(u1,v1),(u2,v2),…,(un,vn),其回归线的斜率和截距的最小二乘估计分别为:
,.
参考答案
一、选择题.
1.B.
解析:因为2位老人相邻,所以可以把他们当成一个整体,有种情况;然后排5个自愿者,有种排法;最后把看成整体的老人插在志愿者形成的4个空隙中,有种排法.由分步计数原理可知共有种排法.
2.A.
解析:根据二项式定理可得第n+1项展开式为,则n=2时,
,所以x2y3的系数为-20.
3.B.
解析:由已知有a≠0,b≠0,因此a,b的取法有种,c的取法有种,即可形成抛物线的条数为.当b=±2时,b2的值相同,重复的抛物线有条;同理,当b=±3时,也有重复的抛物线9条.所以,不同的抛物线有80-9-9=62条.
4.B.
解析:由已知有,即(x-1)2+y2≤1,如图可求得A(1,1),B(1,0),阴影面积等于.
因此所求概率是.
5.C.
解析:先确定哪两张是分给同一人的,有4种方法;再将参观券分下去,有种方法.由分步计数原理可知有4=4×24=96种分法.
6.D.
解析:一共有90个两位数,满足条件的两位数有45个.当个位数为0时,十位数为1,3,5,7,9共5个,因此所求概率为.
7.B.
解析:用表示ξ零件的长度,根据正态分布的性质得:
P(3<ξ<6)=[P(-6<ξ<6)-P(-3<ξ<3)]
=[95.44%-68.26%]=13.59%.
8.A.
解析:由题意有
.
方差
9.C.
解析:观察散点图,利用正相关和负相关的概念即可判断.
10.D.
解析:根据公式,将数据分别代入计算可得.
11.ABCD.
解析:由回归方程可知,y随x的增大而增大,所以y与x具有正的线性相关关系,
A选项正确;由最小二乘法建立回归方程的过程,可知,因此回归直线必过样本中心,B选项正确;由回归方程可知身高每增加1
cm,体重约增加0.85
kg,C选项正确;若某女生身高为170
cm,根据回归方程可近似认为体重为58.79
kg,D选项正确.
12.ACD.
解析:由球的体积公式可知A选项正确;两组数据的平均数相等,方差可能不相等,B选项错误;直线x+y+1=0到圆x2+y2=的距离为,因此直线与圆相切,C选项正确;f(x)=|(ax-1)x|的图象恒过原点,当a=0时,f(x)=|x|在区间(0,+∞)内单调递增;当a<0时,函数g(x)=(ax-1)x的对称轴x=<0,则f(x)=|(ax-1)x|在区间(0,+∞)内单调递增;当a>0时,g(x)=(ax-1)x的对称轴x=>0,由图象可知,在区间(0,+∞)内不是单调递增的,D选项正确.
13.ABD.
解析:P(M)=,P(N)=,若M,N为相互独立事件,则由相互独立事件的乘法公式可知P(MN)=,可知A、B选项正确;C选项中,由P(M)=,P()=,若M,N为相互独立事件,则P(MN)=,该选项错误;D选项中,若M,N为互斥事件,且P(M)=,P(N)=,则P(MN)=+=,该选项正确.
二、填空题
14.169石.
解析:依题意,这批米内夹谷约为×1
534=169石.
15.A.
解析:由丙说可知,乙至少去过A,B,C中的一个城市,由甲说可知,甲去过A,C且比乙去过的城市多,故乙只去过一个城市,且没去过C城市,故乙只去过A城市.
16.2.
解析:展开式的通项为,令12-3r=3,得r=3,所以由=20得ab=1,从而a2+b2≥2ab=2,当且仅当a=b时,a2+b2的最小值为2.
17..
解析:y=|x+1|-|x-2|=解得|x+1|-|x-2|≥1的解集为
[1,+∞).而在[-3,3]上满足不等式的x取值范围为[1,3],故所求概率为.
18..
解析:硬币投掷6次,有三类情况,①正面次数比反面次数多;②反面次数比正面次数多;③正面次数和反面次数一样多,其概率为,①②的概率显然相同,故①的概率为.
三、解答题
19.解:(1)由题意可知,X可取3,4,5,6,且
P(X=3)==,P(X=4)==,P(X=5)==,P(X=6)==.
因此X的分布列为:
X
3
4
5
6
P
(2)由(1)知,
E(X)=3·P(X=3)+3·P(X=3)+4·P(X=4)+5·P(X=5)+6·P(X=6)=.
20.解:(1)×4
500=90.所以应该收集90位女生的样本数据.
(2)由频率分布直方图得
P(X>4)=2(0.15+0.125+0.075+0.025)=0.75.
所以该校学生每周平均体育运动时间超过4小时的概率的估计值为0.75.
(3)每周平均运动时间与性别列联表如下:
运动超过4小时
运动不超过4小时
合计
男生
165
45
210
女生
60
30
90
合计
225
75
300
因此
χ2==≈4.762>3.841.
所以,有95%的把握认为“该校学生的每周平均体育运动时间与性别有关”.
21.解:(1)P(X=-200)==;
P(X=10)==;
P(X=20)==;
P(X=100)==;
所以X的分布列为:
X
-200
10
20
100
P
(2)由(1)可知,玩一盘游戏,没有音乐出现的概率为P0=;则玩三盘游戏,至少有一盘出现音乐的概率为P=;
(3)由(1)可得,E(X)=(-200)·+10·+20·+100·=-,每盘所得分数的期望为负数,所以玩得越多,所得分数越少的可能性越大.
22.解:由题意可知ζ=2,3,4,5,6,所以
P(ζ=2)=×=,P(ζ=3)=2××=,P(ζ=4)=×+2××=,P(ζ=5)=2××=,P(ζ=6)=×=;
所以ζ的分布列为:
ζ
2
3
4
5
6
P
(2)由题意知η的分布列为:
η
1
2
3
P
所以E(η)=++=,
D(η)=,
化简得解得a=3c,b=2c,故a∶b∶c=3∶2∶1.
23.解:(1)由散点图及所给图象可知,y=c+适合作为年销售y关于年宣传费用x的回归方程类型;
(2)令w=,建立y关于w的线性回归方程,由于
==68,
所以=563-68×6.8=100.6.y关于w的线性回归方程为=100.6+68w.
(3)(i)由(2)知,当x=49时,年销售量y的预报值
=100.6+=576.6,
=576.6×0.2-49=66.32.
(ii)根据(2)的结果知,年利润z的预报值
=0.2(100.6+)-x=-x++20.12,
所以当==6.8,即x=46.24时,取得最大值.
故宣传费用为46.24千元时,年利润的预报值最大.
