2021—2022学年人教版数学八年级上册12.1全等三角形课件(28张ppt)
文档属性
| 名称 | 2021—2022学年人教版数学八年级上册12.1全等三角形课件(28张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 403.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-07 00:00:00 | ||
图片预览




文档简介
(共28张PPT)
12.1全等三角形
八年级上册
整理你所学过或知道的三角形的有关知识;
能找准全等三角形的对应边,理解全等三角形的对应角相等;
1
2
3
4
理解并掌握全等三角形的概念及其基本性质;
能进行简单的推理和计算,并解决一些实际问题.
本节目标
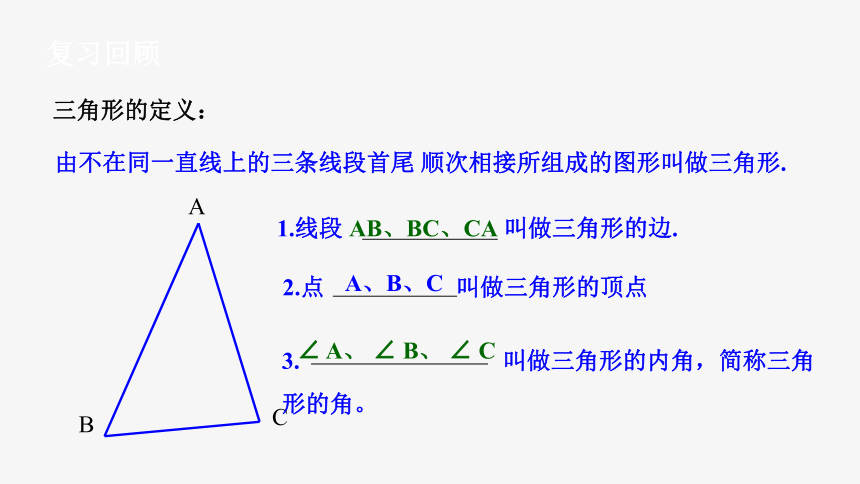
复习回顾
由不在同一直线上的三条线段首尾
顺次相接所组成的图形叫做三角形.
A
C
B
1.线段
叫做三角形的边.
2.点
叫做三角形的顶点
3.
叫做三角形的内角,简称三角形的角。
三角形的定义:
AB、BC、CA
A、B、C
∠
A、
∠
B、
∠
C
观察与思考
下列各组图形的形状与大小有什么特点?
(1)
(2)
(3)
(4)
(5)
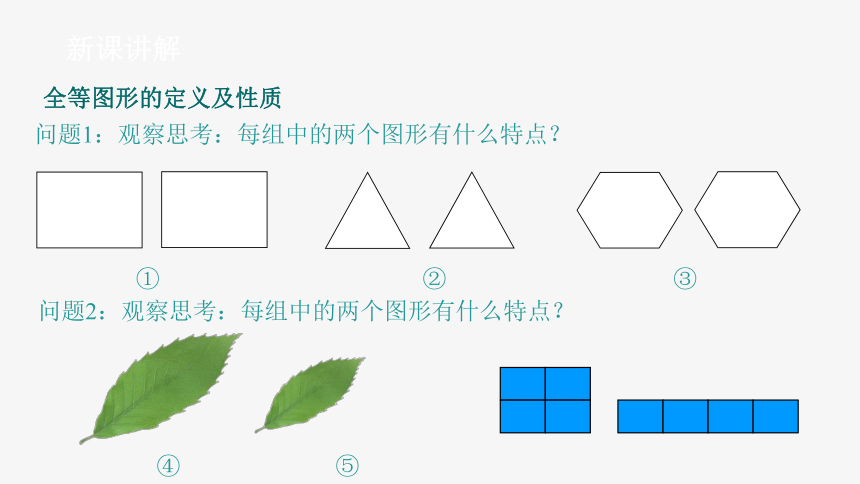
新课讲解
问题1:观察思考:每组中的两个图形有什么特点?
①
②
③
问题2:观察思考:每组中的两个图形有什么特点?
④
⑤
全等图形的定义及性质
全等图形定义:
能够完全重合的两个图形叫做全等图形.
全等形性质:
如果两个图形全等,它们的形状和大小一定都相等.
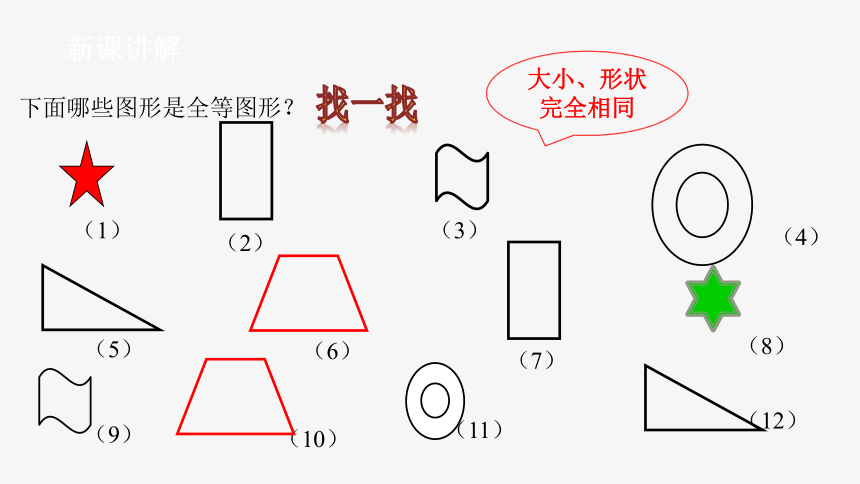
归纳总结
下面哪些图形是全等图形?
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(9)
(10)
(11)
(12)
大小、形状完全相同
找一找
新课讲解
E
D
F
E
D
F
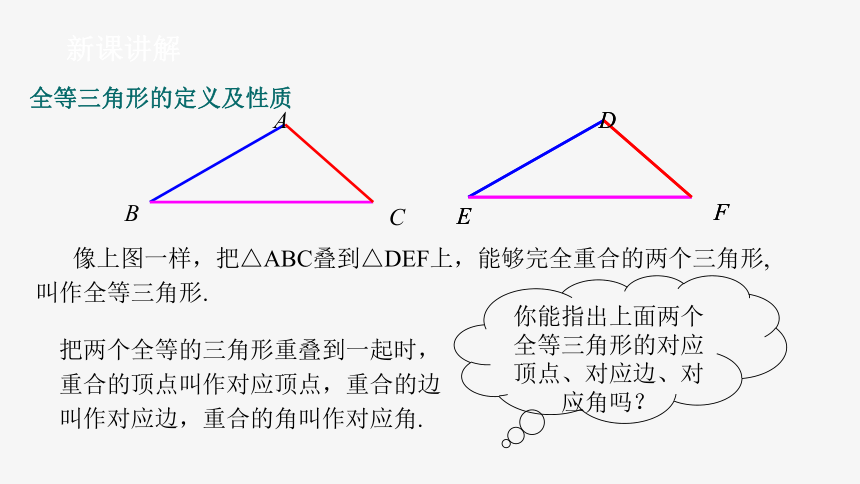
全等三角形的定义及性质
A
B
C
像上图一样,把△ABC叠到△DEF上,能够完全重合的两个三角形,叫作全等三角形.
把两个全等的三角形重叠到一起时,重合的顶点叫作对应顶点,重合的边叫作对应边,重合的角叫作对应角.
你能指出上面两个全等三角形的对应顶点、对应边、对应角吗?
新课讲解
A
A
C
B
D
E
A
B
D
C
A
B
C
D
B
C
N
M
F
E
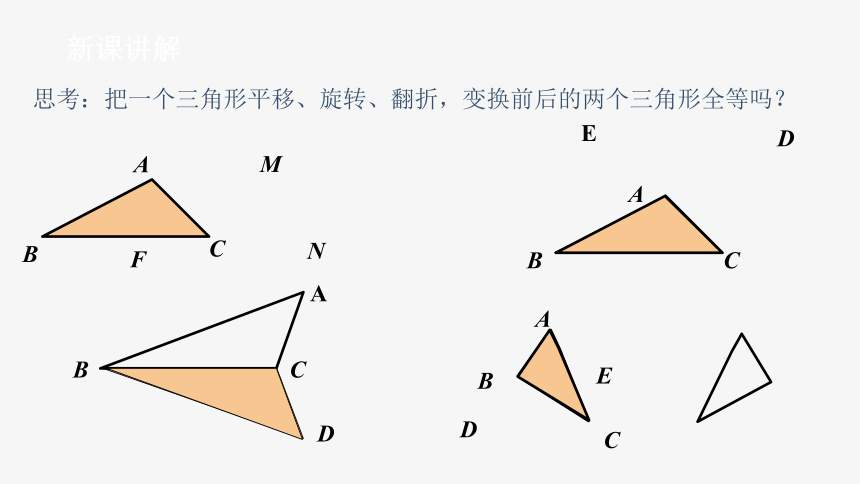
思考:把一个三角形平移、旋转、翻折,变换前后的两个三角形全等吗?
新课讲解
全等三角形的对应边相等,对应角相等
全等三角形的性质
一个图形经过平移、翻折、旋转后,
_
__变化了,但___和__都没有改变,即平移、翻折、旋转前后的两个图形___.
形状
大小
全等
位置
全等变化
归纳总结
△ABC≌△FDE
A
B
C
E
D
F
注意:记两个三角形全等时,通常把表示对应顶点的字母写在对应的位置上.
全等的表示方法
“全等”用符号“≌”表示,读作“全等于”.
新课讲解
例1:如图,若△BOD≌△COE,∠B=∠C,指出这两个全等三角形的对应边;若△ADO≌△AEO,指出这两个三角形的对应角.
解:△BOD与△COE的对应边为:
BO与CO,OD与OE,BD与CE;
△ADO与△AEO的对应角为:
∠DAO与∠EAO,∠ADO与∠AEO,
∠AOD与∠AOE.
例题+变式:全等三角形
A
D
F
C
E
B
1
2
A
B
D
C
1
4
2
3
E
A
B
C
F
1
2
3
4
找一找下列全等图形的对应元素?
A
B
C
D
F
例题+变式:全等三角形
请你利用自制的一对全等三角形拼出有公共顶点或公共边或公共角的图形.试用全等符号表示它们,分析每个图形,找准对应边、对应角.
A
B
C
D
A
B
C
D
A
B
C
D
1.有公共边
寻找对应边、对应角有什么规律?
探究归纳
1.
有公共边,则公共边为对应边;
2.
有公共角(对顶角),则公共角(对顶角)为对应角;
3.最大边与最大边(最小边与最小边)为对应边;
最大角与最大角(最小角与最小角)为对应角;
4.
对应角的对边为对应边;对应边的对角为对应角.
A
B
C
D
O
A
B
C
D
O
A
B
C
D
E
A
B
D
C
E
2.有公共点
总结归纳
探究归纳
A
B
C
E
D
F
∵△ABC≌△DEF(已知),
∴AB=DE,
AC=DF,BC=EF(全等三角形对应边相等),
∠A=∠D,
∠B=∠E,
∠C=∠F(全等三角形对应角相等).
全等三角形的对应边相等;
全等三角形的对应角相等.
全等的性质
新课讲解
∵△ABC≌△FDE
∴A
B=F
D,A
C=F
E,B
C=D
E(全等三角形对应边相等)
∠A=∠F,∠B=∠D,∠C=∠E(全等三角形对应角相等)
A
B
C
E
D
F
全等三角形的性质的几何语言
新课讲解
试一试:
如图,△ABC与△ADC全等,请用数学符号表示出
这两个三角形全等,并写出相等的边和角.
解:△ABC≌△ADC;
相等的边为:AB=AD,AC=AC,BC=DC;
相等的角为:∠BAC=∠DAC,∠B=∠D,∠ACB=∠ACD.
新课讲解
例2
如图,△ABC≌△DEF,∠A=70°,∠B=50°,BF=4,EF=7,求∠DEF的度数和CF的长.
解:∵△ABC≌△DEF,∠A=70°,
∠B=50°,BF=4,EF=7,
∴∠DEF=∠B=50°,BC=EF=7,
∴CF=BC-BF=7-4=3.
例题+变式:全等三角形的性质
例3
如图,△EFG≌△NMH,EF=2.1cm,EH=1.1cm,NH=3.3cm.
(1)试写出两三角形的对应边、对应角;
解:(1)对应边有EF和NM,FG和MH,EG和NH;应角有∠E和∠N,
∠F和∠M,
∠EGF和∠NHM.
例题+变式:全等三角形的性质
(2)求线段NM及HG的长度;
(3)观察图形中对应线段的数量或位置关系,试提出一个正确的结论并证明.
解:∵
△EFG≌△NMH,
∴NM=EF=2.1cm,EG=NH=3.3cm.
∴HG=EG
–EH=3.3-1.1=2.2(cm).
解:结论:EF∥NM
证明:
∵
△EFG≌△NMH,
∴
∠E=∠N.
∴
EF∥NM.
想一想:你还能得出
其他结论吗?
例题+变式:全等三角形的性质
课堂练习
1.能够
的两个图形叫做全等形.两个三角形
重合时,
互相
的顶点叫做对应顶点.记两个全等三角形时,通常把表示
顶点的字母写在
的位置上.
重合
重合
重合
相对应
2.如图,△ABC≌
△ADE,若∠D=∠B,
∠C=
∠AED,
则∠DAE=
;
∠DAB=
.
∠BAC
∠EAC
A
B
C
D
E
3.如图,△ABC≌△BAD,如果AB=5cm,
BD=
4cm,AD=6cm,那么BC的长是(
)
A.6cm
B.5cm
C.4cm
D.无法确定
4.在上题中,∠CAB的对应角是
(
)
A.∠DAB
B.∠DBA
C.∠DBC
D.∠CAD
A
O
C
D
B
A
B
课堂练习
5.如图,△ABC≌△AED,AB是△ABC的最大边,AE是△AED的最大边,
∠BAC
与∠
EAD是对应角,且∠BAC=25°,∠B=
35°,AB=3cm,
BC=1cm,求出∠E,
∠
ADE的度数和线段DE,AE
的长度.
B
C
E
D
A
解:∵
△ABC≌△AED,(已知)
∴∠E=
∠B=
35°,(全等三角形对应角相等)
∠ADE=∠ACB=180°-25°-35°
=120
°,
(全等三角形对应角相等)
DE=BC=1cm,
AE=AB=3cm.
(全等三角形对应边相等)
课堂练习
摆一摆:利用平移,翻折,旋转等变换所得到的三角形与原三角形组成各种各样新的图形,你还能拼出什么不同的造型吗?比一比看谁更有创意!
拓展提升
拼接的图形展示
拓展提升
本节总结
全等
三角形
定义
能够完全重合的两个三角形叫做全等三角形
基本性质
对应边相等
对应角相等
对应元素确定方法
对应边
对应角
长对长,短对短,中对中
公共边一定是对应边
大角对大角,小角对小角
公共角一定是对应角
对顶角一定是对应角
再见
12.1全等三角形
八年级上册
整理你所学过或知道的三角形的有关知识;
能找准全等三角形的对应边,理解全等三角形的对应角相等;
1
2
3
4
理解并掌握全等三角形的概念及其基本性质;
能进行简单的推理和计算,并解决一些实际问题.
本节目标
复习回顾
由不在同一直线上的三条线段首尾
顺次相接所组成的图形叫做三角形.
A
C
B
1.线段
叫做三角形的边.
2.点
叫做三角形的顶点
3.
叫做三角形的内角,简称三角形的角。
三角形的定义:
AB、BC、CA
A、B、C
∠
A、
∠
B、
∠
C
观察与思考
下列各组图形的形状与大小有什么特点?
(1)
(2)
(3)
(4)
(5)
新课讲解
问题1:观察思考:每组中的两个图形有什么特点?
①
②
③
问题2:观察思考:每组中的两个图形有什么特点?
④
⑤
全等图形的定义及性质
全等图形定义:
能够完全重合的两个图形叫做全等图形.
全等形性质:
如果两个图形全等,它们的形状和大小一定都相等.
归纳总结
下面哪些图形是全等图形?
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(9)
(10)
(11)
(12)
大小、形状完全相同
找一找
新课讲解
E
D
F
E
D
F
全等三角形的定义及性质
A
B
C
像上图一样,把△ABC叠到△DEF上,能够完全重合的两个三角形,叫作全等三角形.
把两个全等的三角形重叠到一起时,重合的顶点叫作对应顶点,重合的边叫作对应边,重合的角叫作对应角.
你能指出上面两个全等三角形的对应顶点、对应边、对应角吗?
新课讲解
A
A
C
B
D
E
A
B
D
C
A
B
C
D
B
C
N
M
F
E
思考:把一个三角形平移、旋转、翻折,变换前后的两个三角形全等吗?
新课讲解
全等三角形的对应边相等,对应角相等
全等三角形的性质
一个图形经过平移、翻折、旋转后,
_
__变化了,但___和__都没有改变,即平移、翻折、旋转前后的两个图形___.
形状
大小
全等
位置
全等变化
归纳总结
△ABC≌△FDE
A
B
C
E
D
F
注意:记两个三角形全等时,通常把表示对应顶点的字母写在对应的位置上.
全等的表示方法
“全等”用符号“≌”表示,读作“全等于”.
新课讲解
例1:如图,若△BOD≌△COE,∠B=∠C,指出这两个全等三角形的对应边;若△ADO≌△AEO,指出这两个三角形的对应角.
解:△BOD与△COE的对应边为:
BO与CO,OD与OE,BD与CE;
△ADO与△AEO的对应角为:
∠DAO与∠EAO,∠ADO与∠AEO,
∠AOD与∠AOE.
例题+变式:全等三角形
A
D
F
C
E
B
1
2
A
B
D
C
1
4
2
3
E
A
B
C
F
1
2
3
4
找一找下列全等图形的对应元素?
A
B
C
D
F
例题+变式:全等三角形
请你利用自制的一对全等三角形拼出有公共顶点或公共边或公共角的图形.试用全等符号表示它们,分析每个图形,找准对应边、对应角.
A
B
C
D
A
B
C
D
A
B
C
D
1.有公共边
寻找对应边、对应角有什么规律?
探究归纳
1.
有公共边,则公共边为对应边;
2.
有公共角(对顶角),则公共角(对顶角)为对应角;
3.最大边与最大边(最小边与最小边)为对应边;
最大角与最大角(最小角与最小角)为对应角;
4.
对应角的对边为对应边;对应边的对角为对应角.
A
B
C
D
O
A
B
C
D
O
A
B
C
D
E
A
B
D
C
E
2.有公共点
总结归纳
探究归纳
A
B
C
E
D
F
∵△ABC≌△DEF(已知),
∴AB=DE,
AC=DF,BC=EF(全等三角形对应边相等),
∠A=∠D,
∠B=∠E,
∠C=∠F(全等三角形对应角相等).
全等三角形的对应边相等;
全等三角形的对应角相等.
全等的性质
新课讲解
∵△ABC≌△FDE
∴A
B=F
D,A
C=F
E,B
C=D
E(全等三角形对应边相等)
∠A=∠F,∠B=∠D,∠C=∠E(全等三角形对应角相等)
A
B
C
E
D
F
全等三角形的性质的几何语言
新课讲解
试一试:
如图,△ABC与△ADC全等,请用数学符号表示出
这两个三角形全等,并写出相等的边和角.
解:△ABC≌△ADC;
相等的边为:AB=AD,AC=AC,BC=DC;
相等的角为:∠BAC=∠DAC,∠B=∠D,∠ACB=∠ACD.
新课讲解
例2
如图,△ABC≌△DEF,∠A=70°,∠B=50°,BF=4,EF=7,求∠DEF的度数和CF的长.
解:∵△ABC≌△DEF,∠A=70°,
∠B=50°,BF=4,EF=7,
∴∠DEF=∠B=50°,BC=EF=7,
∴CF=BC-BF=7-4=3.
例题+变式:全等三角形的性质
例3
如图,△EFG≌△NMH,EF=2.1cm,EH=1.1cm,NH=3.3cm.
(1)试写出两三角形的对应边、对应角;
解:(1)对应边有EF和NM,FG和MH,EG和NH;应角有∠E和∠N,
∠F和∠M,
∠EGF和∠NHM.
例题+变式:全等三角形的性质
(2)求线段NM及HG的长度;
(3)观察图形中对应线段的数量或位置关系,试提出一个正确的结论并证明.
解:∵
△EFG≌△NMH,
∴NM=EF=2.1cm,EG=NH=3.3cm.
∴HG=EG
–EH=3.3-1.1=2.2(cm).
解:结论:EF∥NM
证明:
∵
△EFG≌△NMH,
∴
∠E=∠N.
∴
EF∥NM.
想一想:你还能得出
其他结论吗?
例题+变式:全等三角形的性质
课堂练习
1.能够
的两个图形叫做全等形.两个三角形
重合时,
互相
的顶点叫做对应顶点.记两个全等三角形时,通常把表示
顶点的字母写在
的位置上.
重合
重合
重合
相对应
2.如图,△ABC≌
△ADE,若∠D=∠B,
∠C=
∠AED,
则∠DAE=
;
∠DAB=
.
∠BAC
∠EAC
A
B
C
D
E
3.如图,△ABC≌△BAD,如果AB=5cm,
BD=
4cm,AD=6cm,那么BC的长是(
)
A.6cm
B.5cm
C.4cm
D.无法确定
4.在上题中,∠CAB的对应角是
(
)
A.∠DAB
B.∠DBA
C.∠DBC
D.∠CAD
A
O
C
D
B
A
B
课堂练习
5.如图,△ABC≌△AED,AB是△ABC的最大边,AE是△AED的最大边,
∠BAC
与∠
EAD是对应角,且∠BAC=25°,∠B=
35°,AB=3cm,
BC=1cm,求出∠E,
∠
ADE的度数和线段DE,AE
的长度.
B
C
E
D
A
解:∵
△ABC≌△AED,(已知)
∴∠E=
∠B=
35°,(全等三角形对应角相等)
∠ADE=∠ACB=180°-25°-35°
=120
°,
(全等三角形对应角相等)
DE=BC=1cm,
AE=AB=3cm.
(全等三角形对应边相等)
课堂练习
摆一摆:利用平移,翻折,旋转等变换所得到的三角形与原三角形组成各种各样新的图形,你还能拼出什么不同的造型吗?比一比看谁更有创意!
拓展提升
拼接的图形展示
拓展提升
本节总结
全等
三角形
定义
能够完全重合的两个三角形叫做全等三角形
基本性质
对应边相等
对应角相等
对应元素确定方法
对应边
对应角
长对长,短对短,中对中
公共边一定是对应边
大角对大角,小角对小角
公共角一定是对应角
对顶角一定是对应角
再见
