7.7动能和动能定理
图片预览






文档简介
(共43张PPT)
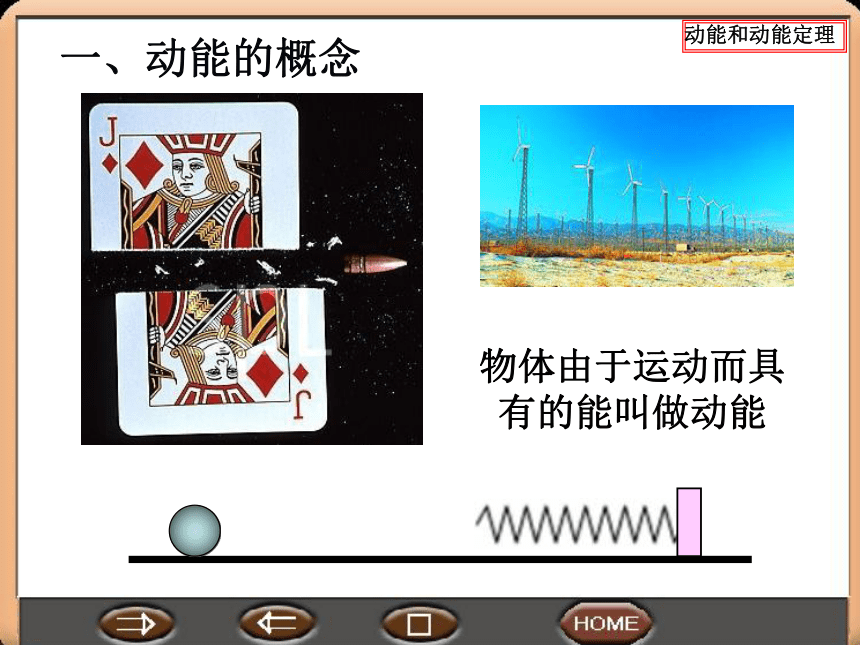
一、动能的概念
物体由于运动而具有的能叫做动能
思考
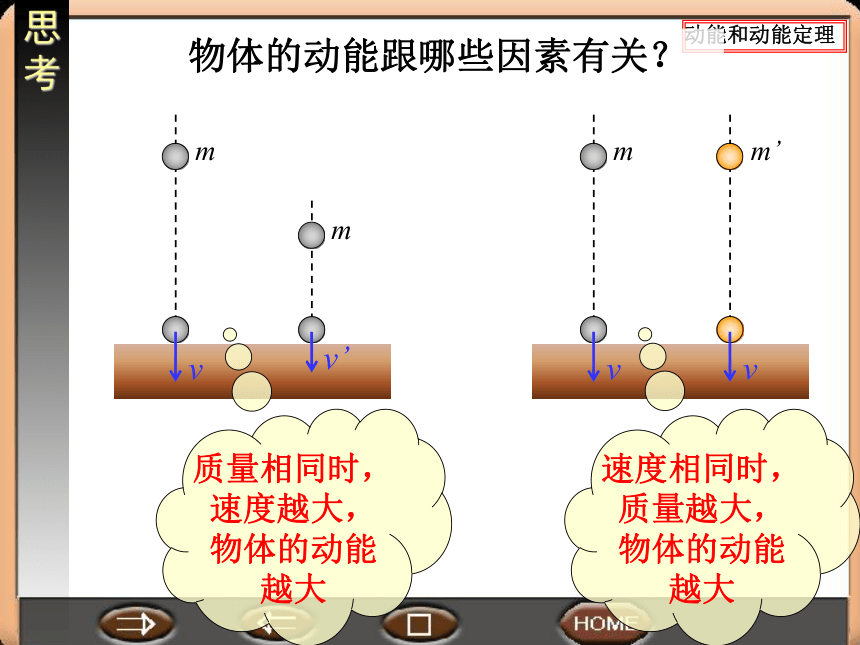
物体的动能跟哪些因素有关?
m
m
v
v’
m
m’
v
v
速度相同时,质量越大,物体的动能越大
质量相同时,速度越大,物体的动能越大
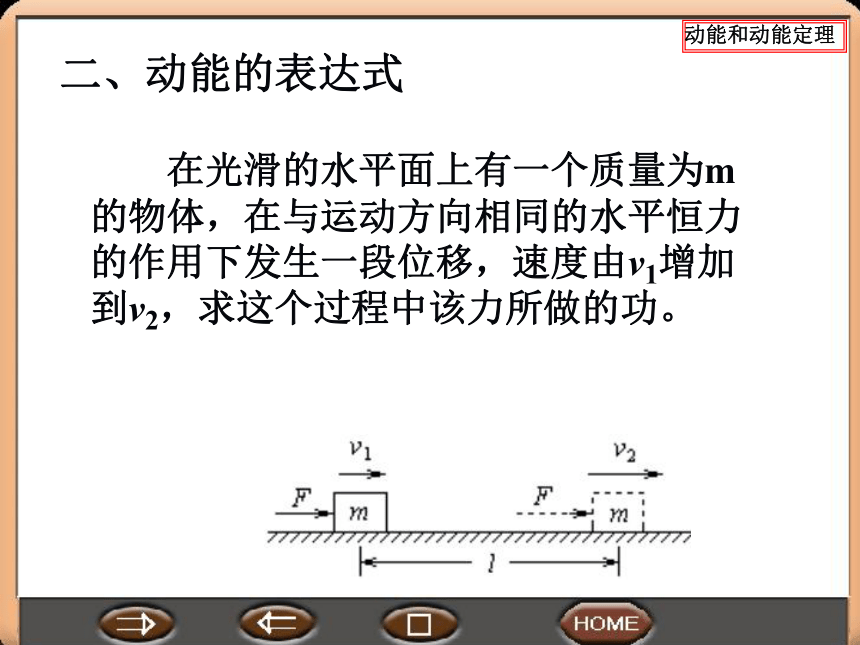
二、动能的表达式
在光滑的水平面上有一个质量为m的物体,在与运动方向相同的水平恒力的作用下发生一段位移,速度由v1增加到v2,求这个过程中该力所做的功。
二、动能的表达式
二、动能的表达式
物体的动能等于物体的质量与物体速度的二次方的乘积的一半。
单位:J
标量
1、我国发射的第一颗人造地球卫星,质量为173 kg,轨道速度为7.2km/s,求它的动能是多少
例与练
2、关于动能,下列说法正确的是( ) A、动能不变的物体,一定处于平衡状态
B、动能不可能是负的
C、一定质量的物体,动能变化时,速度一定变化;但速度变化时,动能不一定变化
D、物体做匀速圆周运动,其动能不变
例与练
力在一个过程中对物体所做的功,等于物体在这个过程中动能的变化。
三、动能定理
动能定理
W合=Ek2-Ek1
合力做的功
末态的动能
初态的动能
W合= -
mv12
1
2
mv22
1
2
动能定理:合力对物体所做的功等于物体动能的变化。
1、合力做正功,即W合>0,Ek2>Ek1 ,动能增大
2、合力做负功,即W合<0,Ek2<Ek1 ,动能减小
三、动能定理
(1)W合是外力所做的总功
3、理解:
【例1】一架喷气式飞机,质量m =5×103kg,起飞过程中从静止开始滑跑的路程为L=5.3×102m时,达到起飞的速度 v =60m/s,在此过程中飞机受到的平均阻力是飞机重量的0.02倍,求飞机受到的牵引力。
析与解
mg
N
F
f
三、动能定理
3、理解:
【例2】一辆质量m、速度为vo的汽车在关闭发动机后于水平地面滑行了距离L后停了下来,试求汽车受到的阻力大小。
析与解
mg
N
f
三、动能定理
(2)动能定理也适用于曲线运动
3、理解:
【例3】某同学从高为h 处以速度v0 水平抛出一个铅球,求铅球落地时速度大小。
v0
v
mg
三、动能定理
(3)动能定理也适用于变力做功
3、理解:
【例4】一质量为m的小球,用长为L的轻绳悬挂于天花板上,小球在水平力F的作用下,从最低点P点缓慢地移到Q点,此时绳子转过了θ角,如图所示,则力F做的功为( )
A.mgLcosθ B.mgL(1-cosθ)
C.FLsinθ D.FLθ
mg
T
变力
三、动能定理
(3)动能定理也适用于变力做功
3、理解:
【例4】一质量为m的小球,用长为L的轻绳悬挂于天花板上,小球在水平力F的作用下,从最低点P点缓慢地移到Q点,此时绳子转过了θ角,如图所示,则力F做的功为( )
mg
T
h
h= L(1-cosθ)
WG= - mgL(1-cosθ)
WF= - WG = mgL(1-cosθ)
WF+ WG = 0-0
变力
求变力做功问题 瞬间力做功问题
运动员踢球的平均作用力为200N,把一个静止的质量为1kg的球以10m/s的速度踢出,水平面上运动60m后停下,则运动员对球做的功 如果运动员踢球时球以10m/s迎面飞来,踢出速度仍为10m/s,则运动员对球做的功为多少
F
S=60m
vo
v=0
质量为m的汽车发动机的功率恒为P,摩擦阻力恒为f,牵引力为F.汽车由静止开始,经过时间t行驶了位移s时,速度达到最大值vm,则发动机所做的功为:
A.Pt B.fvmt C.
D.
E.Fs
ABCD
注意: 做选择题时要注意表达式的多种可能性
求变力做功问题 (与机车相联系的问题)
三、动能定理
(4)可以对全过程用动能定理
3、理解:
【例5】质量为m的小球从距沙坑表面h高处自由落下,进入沙坑,小球在沙坑中运动的最大深度为d,求小球在沙坑中运动受到的平均阻力大小。
对全过程:
h
d
mg
mg
f
三、动能定理
(1)确定研究对象,画出过程示意图;
4、应用动能定理解题的一般步骤:
(2)分析物体的受力,明确各力做功的情况,并确定外力所做的总功;
(3)分析物体的运动,明确物体的初、末状态,确定初、末状态的动能及动能的变化;
(4)根据动能定理列方程求解;
1、同一物体分别从高度相同,倾角不同的光滑斜面的顶端滑到底端时,相同的物理量是( )
A.动能
B.速度
C.速率
D.重力所做的功
例与练
2、质量为m=3kg的物体与水平地面之间的动摩擦因数μ=0.2,在水平恒力F=9N作用下起动,当m位移L1=8m时撤去推力F,问:物体还能滑多远?(g=10m/s2)
例与练
对全过程用动能定理:
L1
L2
F
mg
N
f
3、民航客机机舱紧急出口的气囊是一条连接出口与地面的斜面,高3.2m,长5.5m,质量是60Kg的人沿斜面滑下时所受阻力是240N,求人滑至底端时的速度。
例与练
mg
N
f
3、民航客机机舱紧急出口的气囊是一条连接出口与地面的斜面,高3.2m,长5.5m,质量是60Kg的人沿斜面滑下时所受阻力是240N,求人滑至底端时的速度。
例与练
mg
N
f
牛顿第二定律是矢量式,反映的是力与加速度的瞬时关系;
动能定理是标量式,反映做功过程中总功与始末状态动能变化的关系。
动能定理和牛顿第二定律是研究物体运动问题的两种不同的方法。
四、动能定理与牛顿第二定律
动能定理不涉及物体运动过程中的加速度和时间,对变力做功和多过程问题用动能定理处理问题有时很方便。
4、两个初速度相同的木块A、B质量之比为mA:mB=1:2, A、B与水平地面间的动摩擦因数之比为μA:μB=2:3 ,则A、B在水平地面滑行距离LA:LB为( )
A、 1:2 B、 2:3
C、 2:1 D、 3:2
例与练
O
A
B
5、质量为2Kg的物体沿半径为1m的1/4圆弧从最高点A由静止滑下,滑至最低点B时速率为4m/s,求物体在滑下过程中克服阻力所做的功。
例与练
物体在滑下过程中克服阻力所做功4J
A到B由动能定理:
6、如图所示,质量为m的物体,由高h处无初速滑下,至平面上A点静止,不考虑B点处能量转化,若施加平行于路径的外力使物体由A点沿原路径返回C点,则外力至少做功为 ( )
A.mgh B.2mgh C.3mgh D.无法计算
例与练
从C到B到A:
从A到B到C:
一、动能的概念
物体由于运动而具有的能叫做动能
思考
物体的动能跟哪些因素有关?
m
m
v
v’
m
m’
v
v
速度相同时,质量越大,物体的动能越大
质量相同时,速度越大,物体的动能越大
二、动能的表达式
在光滑的水平面上有一个质量为m的物体,在与运动方向相同的水平恒力的作用下发生一段位移,速度由v1增加到v2,求这个过程中该力所做的功。
二、动能的表达式
二、动能的表达式
物体的动能等于物体的质量与物体速度的二次方的乘积的一半。
单位:J
标量
1、我国发射的第一颗人造地球卫星,质量为173 kg,轨道速度为7.2km/s,求它的动能是多少
例与练
2、关于动能,下列说法正确的是( ) A、动能不变的物体,一定处于平衡状态
B、动能不可能是负的
C、一定质量的物体,动能变化时,速度一定变化;但速度变化时,动能不一定变化
D、物体做匀速圆周运动,其动能不变
例与练
力在一个过程中对物体所做的功,等于物体在这个过程中动能的变化。
三、动能定理
动能定理
W合=Ek2-Ek1
合力做的功
末态的动能
初态的动能
W合= -
mv12
1
2
mv22
1
2
动能定理:合力对物体所做的功等于物体动能的变化。
1、合力做正功,即W合>0,Ek2>Ek1 ,动能增大
2、合力做负功,即W合<0,Ek2<Ek1 ,动能减小
三、动能定理
(1)W合是外力所做的总功
3、理解:
【例1】一架喷气式飞机,质量m =5×103kg,起飞过程中从静止开始滑跑的路程为L=5.3×102m时,达到起飞的速度 v =60m/s,在此过程中飞机受到的平均阻力是飞机重量的0.02倍,求飞机受到的牵引力。
析与解
mg
N
F
f
三、动能定理
3、理解:
【例2】一辆质量m、速度为vo的汽车在关闭发动机后于水平地面滑行了距离L后停了下来,试求汽车受到的阻力大小。
析与解
mg
N
f
三、动能定理
(2)动能定理也适用于曲线运动
3、理解:
【例3】某同学从高为h 处以速度v0 水平抛出一个铅球,求铅球落地时速度大小。
v0
v
mg
三、动能定理
(3)动能定理也适用于变力做功
3、理解:
【例4】一质量为m的小球,用长为L的轻绳悬挂于天花板上,小球在水平力F的作用下,从最低点P点缓慢地移到Q点,此时绳子转过了θ角,如图所示,则力F做的功为( )
A.mgLcosθ B.mgL(1-cosθ)
C.FLsinθ D.FLθ
mg
T
变力
三、动能定理
(3)动能定理也适用于变力做功
3、理解:
【例4】一质量为m的小球,用长为L的轻绳悬挂于天花板上,小球在水平力F的作用下,从最低点P点缓慢地移到Q点,此时绳子转过了θ角,如图所示,则力F做的功为( )
mg
T
h
h= L(1-cosθ)
WG= - mgL(1-cosθ)
WF= - WG = mgL(1-cosθ)
WF+ WG = 0-0
变力
求变力做功问题 瞬间力做功问题
运动员踢球的平均作用力为200N,把一个静止的质量为1kg的球以10m/s的速度踢出,水平面上运动60m后停下,则运动员对球做的功 如果运动员踢球时球以10m/s迎面飞来,踢出速度仍为10m/s,则运动员对球做的功为多少
F
S=60m
vo
v=0
质量为m的汽车发动机的功率恒为P,摩擦阻力恒为f,牵引力为F.汽车由静止开始,经过时间t行驶了位移s时,速度达到最大值vm,则发动机所做的功为:
A.Pt B.fvmt C.
D.
E.Fs
ABCD
注意: 做选择题时要注意表达式的多种可能性
求变力做功问题 (与机车相联系的问题)
三、动能定理
(4)可以对全过程用动能定理
3、理解:
【例5】质量为m的小球从距沙坑表面h高处自由落下,进入沙坑,小球在沙坑中运动的最大深度为d,求小球在沙坑中运动受到的平均阻力大小。
对全过程:
h
d
mg
mg
f
三、动能定理
(1)确定研究对象,画出过程示意图;
4、应用动能定理解题的一般步骤:
(2)分析物体的受力,明确各力做功的情况,并确定外力所做的总功;
(3)分析物体的运动,明确物体的初、末状态,确定初、末状态的动能及动能的变化;
(4)根据动能定理列方程求解;
1、同一物体分别从高度相同,倾角不同的光滑斜面的顶端滑到底端时,相同的物理量是( )
A.动能
B.速度
C.速率
D.重力所做的功
例与练
2、质量为m=3kg的物体与水平地面之间的动摩擦因数μ=0.2,在水平恒力F=9N作用下起动,当m位移L1=8m时撤去推力F,问:物体还能滑多远?(g=10m/s2)
例与练
对全过程用动能定理:
L1
L2
F
mg
N
f
3、民航客机机舱紧急出口的气囊是一条连接出口与地面的斜面,高3.2m,长5.5m,质量是60Kg的人沿斜面滑下时所受阻力是240N,求人滑至底端时的速度。
例与练
mg
N
f
3、民航客机机舱紧急出口的气囊是一条连接出口与地面的斜面,高3.2m,长5.5m,质量是60Kg的人沿斜面滑下时所受阻力是240N,求人滑至底端时的速度。
例与练
mg
N
f
牛顿第二定律是矢量式,反映的是力与加速度的瞬时关系;
动能定理是标量式,反映做功过程中总功与始末状态动能变化的关系。
动能定理和牛顿第二定律是研究物体运动问题的两种不同的方法。
四、动能定理与牛顿第二定律
动能定理不涉及物体运动过程中的加速度和时间,对变力做功和多过程问题用动能定理处理问题有时很方便。
4、两个初速度相同的木块A、B质量之比为mA:mB=1:2, A、B与水平地面间的动摩擦因数之比为μA:μB=2:3 ,则A、B在水平地面滑行距离LA:LB为( )
A、 1:2 B、 2:3
C、 2:1 D、 3:2
例与练
O
A
B
5、质量为2Kg的物体沿半径为1m的1/4圆弧从最高点A由静止滑下,滑至最低点B时速率为4m/s,求物体在滑下过程中克服阻力所做的功。
例与练
物体在滑下过程中克服阻力所做功4J
A到B由动能定理:
6、如图所示,质量为m的物体,由高h处无初速滑下,至平面上A点静止,不考虑B点处能量转化,若施加平行于路径的外力使物体由A点沿原路径返回C点,则外力至少做功为 ( )
A.mgh B.2mgh C.3mgh D.无法计算
例与练
从C到B到A:
从A到B到C:
