七年级数学三角形
图片预览









文档简介
(共57张PPT)
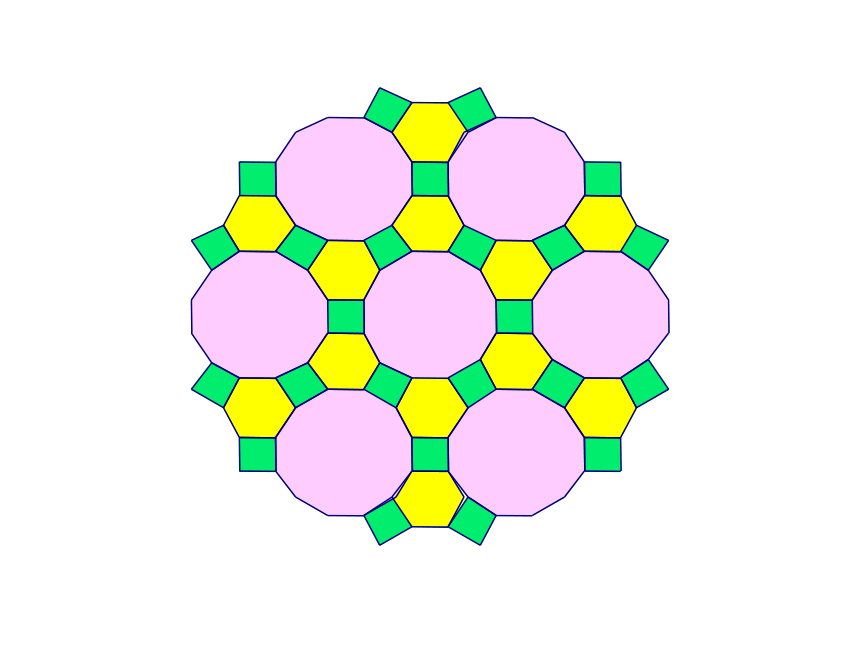
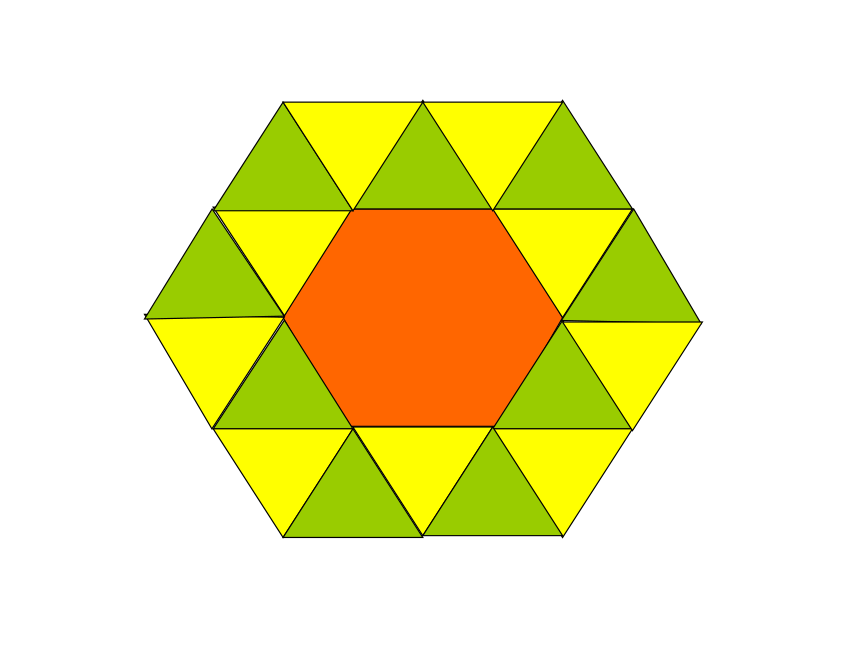
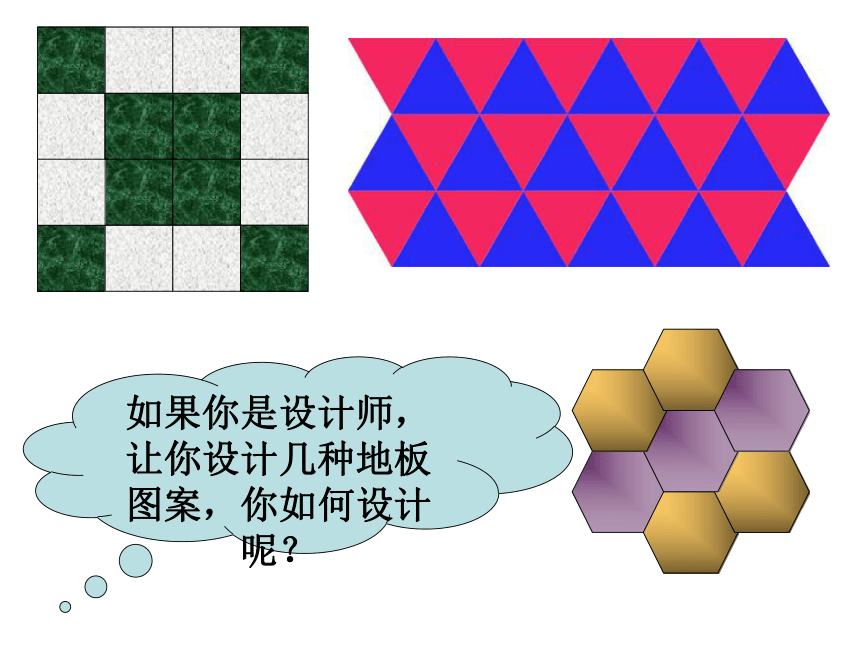
请观察,这些图形在拼接时有什么特点
如果你是设计师,让你设计几种地板图案,你如何设计呢?
平面图形的镶嵌(平面图形的密铺):
用形状和大小完全相同的一种或几种平面图形进行拼接,彼此之间不留空隙、不重叠地铺成一片,这就是平面图形的镶嵌,又称平面图形的密铺.
学一学
镶嵌的两个条件:
1、全等的一种或几种平面图形;
2、无空隙、不重叠铺成一片。
探究
哪些图形可以镶嵌,
哪些图形不可以镶嵌?
探究活动(一)
用形状、大小完全相同的三角形能否镶嵌?
正三角形的平面镶嵌
60°
60°
60°
60°
60°
60°
接点处的六个角和为360°
结论:
形状、大小完全相同的任意
三角形能镶嵌成平面图形。
通过探究我发现:
1.任意全等的三角形都______镶嵌,
2.在每个拼接点处有___个角,而这___个角的和恰好是这个三角形的内角和的___倍,也就是它们的和为____,
可以
六
六
两
360o
探究活动(二)
用同一种四边形可以镶嵌吗?
正方形的平面镶嵌
90°
结论:
形状、大小相同的任意四边形
能镶嵌成平面图形
★通过探究我发现:
1.任意全等的四边形_____镶嵌.
2.在每个拼接点处有___个角,而这___个角的和恰好是这个四边形的四个内角之___,也就是它们的和为____.
可以
四
四
和
360
能镶嵌的图形在一个拼接
点处的特点:
1.各角之和等于360 ,
2.相等的边互相重合。
结论 1
探究活动(三)
2.正六边形能镶嵌吗?说说理由。
1.正五边形能镶嵌吗?说说理由。
3.还能找到能镶嵌的其他图形吗?
做一做
正五边形可以镶嵌吗?
1
2
3
正六边形可以镶嵌吗?
正六边形的平面镶嵌
120 °
120 °
120 °
能否
平面
镶嵌
图形 一个顶点周围正多边形的个数
能
能
能
正三角形
正方形
正五边形
正六边形
6
4
3
不能
正三角形
正方形
正五边形
正六边形
内角和
各个内角
180o
60o
360o
90o
540o
108o
720o
120o
还能找到能密铺的其他正多边形吗?
要用正多边形镶嵌成一个平面的关键是看:这种正多边形的一个内角的倍数是否是360°,在正多边形里,正三角形的每个内角都是60°,正四边形的每个内角都是90°,正六边形的每个内角都是120°,这三种多边形的一个内角的倍数都是360°,而其他的正多边形的每个内角的倍数都不是360°,所以说:在正多边形里只有正三角形、正四边形、正六边形可以密铺,而其他的正多边形不可密铺.
∴解得
仅用一个正多边形进行镶嵌,要嵌成一个平面,必须要求在公共顶点上所有内角和为360度。
能单独镶嵌平面的正多边形只有三种:
正三角形、正四边形、正六边形
令正多边形的边数为n,个数为m,则有
结论1:
可以用同一种正多边形镶嵌的图形只有
正三角形,正四边形,正六边形.
结论2:
用一种形状、大小完全相同的三角形,四边形
也能进行平面镶嵌
正多边形可以镶嵌的条件:
每个内角都能被360o 整除。
探究活动(四)
----创意空间
用同一种平面图形如果不能密铺,用两种或者两种以上平面图形能不能密铺呢
二、用两种正多边形进行平面镶嵌
1、正三角形与正方形
设在一个顶点周围有m个正三角形的角,n个正方形的角,那么这些角的和应该满足方程:
m.60°+ n.90°= 360°
即 2m+ 3n= 12
这个方程的正整数解为m=3,n=2
则记作(3,3,3,4,4)
3个正三角形+2个正方形
二、用两种正多边形进行平面镶嵌
1、正三角形与正六边形
设在一个顶点周围有m个正三角形的角,n个正六边形的角,那么这些角的和应该满足方程:
m.60°+ n.120°= 360°
即 m+ 2n= 6
这个方程的正整数解为m=4,n=1或者m=2,n=2
120°
120°
60°
60°
图案(Ⅰ)
(3,3,6,6)
2个正三角形+2个正六边形
图案(Ⅱ)
60°
60°
120°
60°
60°
每个顶点处正六边形1个,正三角形4个.
(3,3, 3, 3,6)
4个正三角形+1个正六边形
1、如果用正四边形与正八边形,如何镶嵌?
2、如果用正三角形与
正十二边形,如何镶嵌?
正八边形与正方形的平面镶嵌
正十二边形与正三角形的平面镶嵌
1个正三角形+2个正十二边形
1个正方形+2个正八边形
2个正五边形+1个正十边形
收获
当拼接点处的所有角之和是360 时,就能拼成一个平面图形。
思考:
能否用1块正三角形,2块正方形,1块正六边形(边长相同)铺满地面?
正三角形、正方形、正六边形的镶嵌
资料1:用正多边形进行平面镶嵌只有以下这17组解。有书记载说明这17组解是1924年一个叫波尔亚的人给出的。实际上早在此之前,西班牙阿尔汉布拉宫的装饰已经一个不少地制出了这些图样,真是令人叹为观止。
发现二:
用一种形状、大小完全相同的三角形,四边形也能进行
平面镶嵌
发现一:
同一种正多边形进行平面镶嵌的图形只有三种:正三角形、
正方形、正六边形
发现三:
正多边形镶嵌的条件:
(1)同一顶点的各角度数和为360度;
(2)各个正多边形的边长要相等。
用正五边形和什么多边形能密铺?
请观察,这些图形在拼接时有什么特点
如果你是设计师,让你设计几种地板图案,你如何设计呢?
平面图形的镶嵌(平面图形的密铺):
用形状和大小完全相同的一种或几种平面图形进行拼接,彼此之间不留空隙、不重叠地铺成一片,这就是平面图形的镶嵌,又称平面图形的密铺.
学一学
镶嵌的两个条件:
1、全等的一种或几种平面图形;
2、无空隙、不重叠铺成一片。
探究
哪些图形可以镶嵌,
哪些图形不可以镶嵌?
探究活动(一)
用形状、大小完全相同的三角形能否镶嵌?
正三角形的平面镶嵌
60°
60°
60°
60°
60°
60°
接点处的六个角和为360°
结论:
形状、大小完全相同的任意
三角形能镶嵌成平面图形。
通过探究我发现:
1.任意全等的三角形都______镶嵌,
2.在每个拼接点处有___个角,而这___个角的和恰好是这个三角形的内角和的___倍,也就是它们的和为____,
可以
六
六
两
360o
探究活动(二)
用同一种四边形可以镶嵌吗?
正方形的平面镶嵌
90°
结论:
形状、大小相同的任意四边形
能镶嵌成平面图形
★通过探究我发现:
1.任意全等的四边形_____镶嵌.
2.在每个拼接点处有___个角,而这___个角的和恰好是这个四边形的四个内角之___,也就是它们的和为____.
可以
四
四
和
360
能镶嵌的图形在一个拼接
点处的特点:
1.各角之和等于360 ,
2.相等的边互相重合。
结论 1
探究活动(三)
2.正六边形能镶嵌吗?说说理由。
1.正五边形能镶嵌吗?说说理由。
3.还能找到能镶嵌的其他图形吗?
做一做
正五边形可以镶嵌吗?
1
2
3
正六边形可以镶嵌吗?
正六边形的平面镶嵌
120 °
120 °
120 °
能否
平面
镶嵌
图形 一个顶点周围正多边形的个数
能
能
能
正三角形
正方形
正五边形
正六边形
6
4
3
不能
正三角形
正方形
正五边形
正六边形
内角和
各个内角
180o
60o
360o
90o
540o
108o
720o
120o
还能找到能密铺的其他正多边形吗?
要用正多边形镶嵌成一个平面的关键是看:这种正多边形的一个内角的倍数是否是360°,在正多边形里,正三角形的每个内角都是60°,正四边形的每个内角都是90°,正六边形的每个内角都是120°,这三种多边形的一个内角的倍数都是360°,而其他的正多边形的每个内角的倍数都不是360°,所以说:在正多边形里只有正三角形、正四边形、正六边形可以密铺,而其他的正多边形不可密铺.
∴解得
仅用一个正多边形进行镶嵌,要嵌成一个平面,必须要求在公共顶点上所有内角和为360度。
能单独镶嵌平面的正多边形只有三种:
正三角形、正四边形、正六边形
令正多边形的边数为n,个数为m,则有
结论1:
可以用同一种正多边形镶嵌的图形只有
正三角形,正四边形,正六边形.
结论2:
用一种形状、大小完全相同的三角形,四边形
也能进行平面镶嵌
正多边形可以镶嵌的条件:
每个内角都能被360o 整除。
探究活动(四)
----创意空间
用同一种平面图形如果不能密铺,用两种或者两种以上平面图形能不能密铺呢
二、用两种正多边形进行平面镶嵌
1、正三角形与正方形
设在一个顶点周围有m个正三角形的角,n个正方形的角,那么这些角的和应该满足方程:
m.60°+ n.90°= 360°
即 2m+ 3n= 12
这个方程的正整数解为m=3,n=2
则记作(3,3,3,4,4)
3个正三角形+2个正方形
二、用两种正多边形进行平面镶嵌
1、正三角形与正六边形
设在一个顶点周围有m个正三角形的角,n个正六边形的角,那么这些角的和应该满足方程:
m.60°+ n.120°= 360°
即 m+ 2n= 6
这个方程的正整数解为m=4,n=1或者m=2,n=2
120°
120°
60°
60°
图案(Ⅰ)
(3,3,6,6)
2个正三角形+2个正六边形
图案(Ⅱ)
60°
60°
120°
60°
60°
每个顶点处正六边形1个,正三角形4个.
(3,3, 3, 3,6)
4个正三角形+1个正六边形
1、如果用正四边形与正八边形,如何镶嵌?
2、如果用正三角形与
正十二边形,如何镶嵌?
正八边形与正方形的平面镶嵌
正十二边形与正三角形的平面镶嵌
1个正三角形+2个正十二边形
1个正方形+2个正八边形
2个正五边形+1个正十边形
收获
当拼接点处的所有角之和是360 时,就能拼成一个平面图形。
思考:
能否用1块正三角形,2块正方形,1块正六边形(边长相同)铺满地面?
正三角形、正方形、正六边形的镶嵌
资料1:用正多边形进行平面镶嵌只有以下这17组解。有书记载说明这17组解是1924年一个叫波尔亚的人给出的。实际上早在此之前,西班牙阿尔汉布拉宫的装饰已经一个不少地制出了这些图样,真是令人叹为观止。
发现二:
用一种形状、大小完全相同的三角形,四边形也能进行
平面镶嵌
发现一:
同一种正多边形进行平面镶嵌的图形只有三种:正三角形、
正方形、正六边形
发现三:
正多边形镶嵌的条件:
(1)同一顶点的各角度数和为360度;
(2)各个正多边形的边长要相等。
用正五边形和什么多边形能密铺?
