2010-2012高考物理高频考点精选分类解析32 带电粒子在电场、磁场中的运动
文档属性
| 名称 | 2010-2012高考物理高频考点精选分类解析32 带电粒子在电场、磁场中的运动 |  | |
| 格式 | zip | ||
| 文件大小 | 107.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2012-06-22 20:15:57 | ||
图片预览


文档简介
本人声明:本资源属本人原创作品,授予21世纪教育网独家发行。
2010~2012高考物理高频考点精选分类解析
高频考点32 带电粒子在电场、磁场中的运动
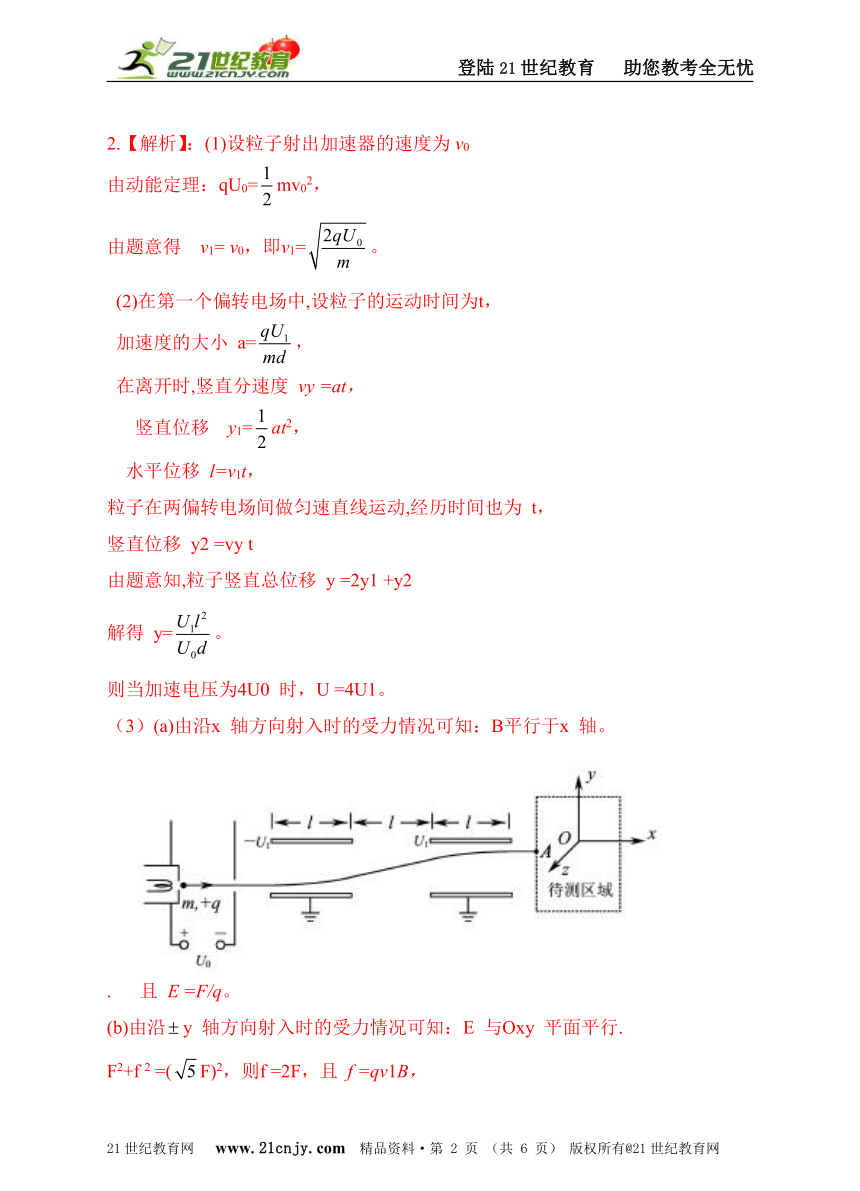
1.(16 分) (2012·江苏物理)如图所示,待测区域中存在匀强电场和匀强磁场,根据带电粒子射入时的受力情况可推测其电场和磁场。 图中装置由加速器和平移器组成,平移器由两对水平放置、相距为l的相同平行金属板构成,极板长度为l、间距为d,两对极板间偏转电压大小相等、电场方向相反。质量为m、电荷量为+q 的粒子经加速电压U0 加速后,水平射入偏转电压为U1 的平移器,最终从A 点水平射入待测区域。不考虑粒子受到的重力。.
(1)求粒子射出平移器时的速度大小v1;
(2)当加速电压变为4U0 时,欲使粒子仍从A 点射入待测区域,求此时的偏转电压U;
(3)已知粒子以不同速度水平向右射入待测区域,刚进入时的受力大小均为F. 现取水平向右为x 轴正方向,,建立如图所示的直角坐标系Oxyz.。保持加速电压为U0 不变,,移动装置使粒子沿不同的坐标轴方向射入待测区域,,粒子刚射入时的受力大小如下表所示.
请推测该区域中电场强度和磁感应强度的大小及可能的方向.。
2.【解析】:(1)设粒子射出加速器的速度为v0
由动能定理:qU0=mv02,
由题意得 v1= v0,即v1=。
(2)在第一个偏转电场中,设粒子的运动时间为t,
加速度的大小 a=,
在离开时,竖直分速度 vy =at,
竖直位移 y1=at2,
水平位移 l=v1t,
粒子在两偏转电场间做匀速直线运动,经历时间也为 t,
竖直位移 y2 =vy t
由题意知,粒子竖直总位移 y =2y1 +y2
解得 y=。
则当加速电压为4U0 时,U =4U1。
(3)(a)由沿x 轴方向射入时的受力情况可知:B平行于x 轴。
. 且 E =F/q。
(b)由沿y 轴方向射入时的受力情况可知:E 与Oxy 平面平行.
F2+f 2 =(F)2,则f =2F,且 f =qv1B,
解得:B=。
(c)设电场方向与x 轴方向夹角为α。.
若B 沿x 轴方向,由沿z 轴方向射入时的受力情况得
(f+Fsinα)2+(Fcosα)2=(F)2,
解得α=30°,或α=150°。
即E与Oxy 平面平行且与x 轴方向的夹角为30°或150°.。
同理,若B 沿-x 轴方向
E 与Oxy 平面平行且与x 轴方向的夹角为-30°或-150°.。
【考点定位】此题考查带电粒子在复合场中的运动。
2.(2011全国理综)如图,与水平面成45°角的平面MN将空间分成I和II两个区域。一质量为m、电荷量为q(q>0)的粒子以速度v0从平面MN上的P0点水平向右射入I区。粒子在I区运动时,只受到大小不变、方向竖直向下的电场作用,电场强度大小为E;在II区运动时,只受到匀强磁场的作用,磁感应强度大小为B,方向垂直于纸面向里。求粒子首次从II区离开时到出发点P0的距离。粒子的重力可以忽略。
【解析】:带电粒子进入电场后,在电场力作用下沿抛物线运动,其加速度方向竖直向下,设其大小为a,由牛顿运动定律得qE=ma ①
经过时间t0,粒子从平面MN上的点P1进入磁场,由运动学公式和几何关系得,
v0t0=at02 ②
粒子速度大小v1为v1=。③
设速度方向与竖直方向的夹角为α,tanα=。④
此时粒子到出发点P0的距离为s0=v0t0 ⑤
此后粒子进入磁场,在洛仑兹力作用下做匀速圆周运动,圆周半径r1=.⑥
设粒子首次离开磁场的点为P2,弧所张的圆心角为2β,则点P1到点P2的距离为
s1=2r1sinβ,⑦
由几何关系得 α+ β=45°⑧
联立①②③④⑥⑦⑧解得s1= ⑨
点P2与点P0相距l=s0+s1 ⑩
联立①②⑤⑨⑩解得l=
【点评】此题考查带电粒子在电场中的类平抛运动和磁场中的匀速圆周运动,难度中等。
3(2011重庆理综卷第25题)某仪器用电场和磁场来控制电子在材料表面上方的运动,如图4所示,材料表面上方矩形区域PP'N'N充满竖直向下的匀强电场,宽为d;矩形区域NN'M'M充满垂直纸面向里的匀强磁场,磁感应强度为B,长为3s,宽为s;NN'为磁场与电场之间的薄隔离层。一个电荷量为e、质量为m、初速为零的电子,从P点开始被电场加速经隔离层垂直进入磁场,电子每次穿越隔离层,运动方向不变,其动能损失是每次穿越前动能的10%,最后电子仅能从磁场边界M'N'飞出。不计电子所受重力。
(1)求电子第二次与第一次圆周运动半径之比;
(2)求电场强度的取值范围;
(3)A是的中点,若要使电子在A、间垂直于A飞出,求电子在磁场区域中运动的时间。
【解析】(1)设圆周运动的半径分别为R1、R2、···R n、R n+1、···,第一和第二次圆周运动速率分别为v1和v2,动能分别为Ek1和Ek2。
由Ek2=0.81 Ek1,R1= ,R2= , Ek1=mv12,Ek2=mv22
解得R2∶R1=0.9
(2)设电场强度为E,第一次到达隔离层前的速率为v’。
由:eEd=mv’2,0.9×mv’2=mv12,R1≤s,
解得E≤。
又由Rn=0.9 n-1 R1,
2 R1(1+0.9+0.92+···+0.9 n+···)>s
解得:E>。
所以电场强度的取值范围为
(3)设电子在匀强磁场中做匀速圆周运动的周期为T,运动的半圆周个数为n,运动的总时间为t。由题意,有:
+ R n+1=3s,
R1≤s,R n+1=0.9 n R 1,R n+1≥s/2,
解得:n=2.
又由:T=,解得t=。
【点评】此题与科技实际结合紧密,情景新颖,难度较大,分值较高。
4.(2010山东理综)如图3所示,以两虚线为边界,中间存在平行纸面且与边界垂直的水平电场,宽度为d,两侧为相同的匀强磁场,方向垂直纸面向里。一质量为m、带电量+q、重力不计的带电粒子,以初速度v1垂直边界射入磁场做匀速圆周运动,后进入电场做匀加速运动,然后第二次进入磁场中运动,此后粒子在电场和磁场中交替运动。已知粒子第二次在磁场中运动的半径是第一次的二倍,第三次是第一次的三倍,以此类推。求
(1)粒子第一次经过电场的过程中电场力所做的功W1。
(2)粒子第n次经过电场时电场强度的大小En。
(3)粒子第n次经过电场所用的时间tn。
(4)假设粒子在磁场中运动时,电场区域场强为零。请画出从粒子第一次射入磁场至第三次离开电场的过程中,电场强度随时间变化的关系图线(不要求写出推导过程,不要求标明坐标刻度值)。
【解析】带电粒子在磁场中做匀速圆周运动,由qvB=mv2/r得r=mv/qB。
则v1∶v2∶…∶vn=r1∶r2∶…∶rn=1∶2∶…∶n
(1)第一次过电场,由动能定理得
(2)第n次经过电场时,由动能定理得
解得En=
(3)第n次经过电场时的平均速度,
则时间为。
(4)根据电场强度的大小的表达式En=,第一次经过电场时,n=1,E1=;第二次经过电场时,n=2,E2=;第三次经过电场时,n=3,E3=;······,注意带电粒子在匀强磁场中运动时间相等,据此可画出电场强度随时间变化的关系图线如图。
2010~2012高考物理高频考点精选分类解析
高频考点32 带电粒子在电场、磁场中的运动
1.(16 分) (2012·江苏物理)如图所示,待测区域中存在匀强电场和匀强磁场,根据带电粒子射入时的受力情况可推测其电场和磁场。 图中装置由加速器和平移器组成,平移器由两对水平放置、相距为l的相同平行金属板构成,极板长度为l、间距为d,两对极板间偏转电压大小相等、电场方向相反。质量为m、电荷量为+q 的粒子经加速电压U0 加速后,水平射入偏转电压为U1 的平移器,最终从A 点水平射入待测区域。不考虑粒子受到的重力。.
(1)求粒子射出平移器时的速度大小v1;
(2)当加速电压变为4U0 时,欲使粒子仍从A 点射入待测区域,求此时的偏转电压U;
(3)已知粒子以不同速度水平向右射入待测区域,刚进入时的受力大小均为F. 现取水平向右为x 轴正方向,,建立如图所示的直角坐标系Oxyz.。保持加速电压为U0 不变,,移动装置使粒子沿不同的坐标轴方向射入待测区域,,粒子刚射入时的受力大小如下表所示.
请推测该区域中电场强度和磁感应强度的大小及可能的方向.。
2.【解析】:(1)设粒子射出加速器的速度为v0
由动能定理:qU0=mv02,
由题意得 v1= v0,即v1=。
(2)在第一个偏转电场中,设粒子的运动时间为t,
加速度的大小 a=,
在离开时,竖直分速度 vy =at,
竖直位移 y1=at2,
水平位移 l=v1t,
粒子在两偏转电场间做匀速直线运动,经历时间也为 t,
竖直位移 y2 =vy t
由题意知,粒子竖直总位移 y =2y1 +y2
解得 y=。
则当加速电压为4U0 时,U =4U1。
(3)(a)由沿x 轴方向射入时的受力情况可知:B平行于x 轴。
. 且 E =F/q。
(b)由沿y 轴方向射入时的受力情况可知:E 与Oxy 平面平行.
F2+f 2 =(F)2,则f =2F,且 f =qv1B,
解得:B=。
(c)设电场方向与x 轴方向夹角为α。.
若B 沿x 轴方向,由沿z 轴方向射入时的受力情况得
(f+Fsinα)2+(Fcosα)2=(F)2,
解得α=30°,或α=150°。
即E与Oxy 平面平行且与x 轴方向的夹角为30°或150°.。
同理,若B 沿-x 轴方向
E 与Oxy 平面平行且与x 轴方向的夹角为-30°或-150°.。
【考点定位】此题考查带电粒子在复合场中的运动。
2.(2011全国理综)如图,与水平面成45°角的平面MN将空间分成I和II两个区域。一质量为m、电荷量为q(q>0)的粒子以速度v0从平面MN上的P0点水平向右射入I区。粒子在I区运动时,只受到大小不变、方向竖直向下的电场作用,电场强度大小为E;在II区运动时,只受到匀强磁场的作用,磁感应强度大小为B,方向垂直于纸面向里。求粒子首次从II区离开时到出发点P0的距离。粒子的重力可以忽略。
【解析】:带电粒子进入电场后,在电场力作用下沿抛物线运动,其加速度方向竖直向下,设其大小为a,由牛顿运动定律得qE=ma ①
经过时间t0,粒子从平面MN上的点P1进入磁场,由运动学公式和几何关系得,
v0t0=at02 ②
粒子速度大小v1为v1=。③
设速度方向与竖直方向的夹角为α,tanα=。④
此时粒子到出发点P0的距离为s0=v0t0 ⑤
此后粒子进入磁场,在洛仑兹力作用下做匀速圆周运动,圆周半径r1=.⑥
设粒子首次离开磁场的点为P2,弧所张的圆心角为2β,则点P1到点P2的距离为
s1=2r1sinβ,⑦
由几何关系得 α+ β=45°⑧
联立①②③④⑥⑦⑧解得s1= ⑨
点P2与点P0相距l=s0+s1 ⑩
联立①②⑤⑨⑩解得l=
【点评】此题考查带电粒子在电场中的类平抛运动和磁场中的匀速圆周运动,难度中等。
3(2011重庆理综卷第25题)某仪器用电场和磁场来控制电子在材料表面上方的运动,如图4所示,材料表面上方矩形区域PP'N'N充满竖直向下的匀强电场,宽为d;矩形区域NN'M'M充满垂直纸面向里的匀强磁场,磁感应强度为B,长为3s,宽为s;NN'为磁场与电场之间的薄隔离层。一个电荷量为e、质量为m、初速为零的电子,从P点开始被电场加速经隔离层垂直进入磁场,电子每次穿越隔离层,运动方向不变,其动能损失是每次穿越前动能的10%,最后电子仅能从磁场边界M'N'飞出。不计电子所受重力。
(1)求电子第二次与第一次圆周运动半径之比;
(2)求电场强度的取值范围;
(3)A是的中点,若要使电子在A、间垂直于A飞出,求电子在磁场区域中运动的时间。
【解析】(1)设圆周运动的半径分别为R1、R2、···R n、R n+1、···,第一和第二次圆周运动速率分别为v1和v2,动能分别为Ek1和Ek2。
由Ek2=0.81 Ek1,R1= ,R2= , Ek1=mv12,Ek2=mv22
解得R2∶R1=0.9
(2)设电场强度为E,第一次到达隔离层前的速率为v’。
由:eEd=mv’2,0.9×mv’2=mv12,R1≤s,
解得E≤。
又由Rn=0.9 n-1 R1,
2 R1(1+0.9+0.92+···+0.9 n+···)>s
解得:E>。
所以电场强度的取值范围为
+ R n+1=3s,
R1≤s,R n+1=0.9 n R 1,R n+1≥s/2,
解得:n=2.
又由:T=,解得t=。
【点评】此题与科技实际结合紧密,情景新颖,难度较大,分值较高。
4.(2010山东理综)如图3所示,以两虚线为边界,中间存在平行纸面且与边界垂直的水平电场,宽度为d,两侧为相同的匀强磁场,方向垂直纸面向里。一质量为m、带电量+q、重力不计的带电粒子,以初速度v1垂直边界射入磁场做匀速圆周运动,后进入电场做匀加速运动,然后第二次进入磁场中运动,此后粒子在电场和磁场中交替运动。已知粒子第二次在磁场中运动的半径是第一次的二倍,第三次是第一次的三倍,以此类推。求
(1)粒子第一次经过电场的过程中电场力所做的功W1。
(2)粒子第n次经过电场时电场强度的大小En。
(3)粒子第n次经过电场所用的时间tn。
(4)假设粒子在磁场中运动时,电场区域场强为零。请画出从粒子第一次射入磁场至第三次离开电场的过程中,电场强度随时间变化的关系图线(不要求写出推导过程,不要求标明坐标刻度值)。
【解析】带电粒子在磁场中做匀速圆周运动,由qvB=mv2/r得r=mv/qB。
则v1∶v2∶…∶vn=r1∶r2∶…∶rn=1∶2∶…∶n
(1)第一次过电场,由动能定理得
(2)第n次经过电场时,由动能定理得
解得En=
(3)第n次经过电场时的平均速度,
则时间为。
(4)根据电场强度的大小的表达式En=,第一次经过电场时,n=1,E1=;第二次经过电场时,n=2,E2=;第三次经过电场时,n=3,E3=;······,注意带电粒子在匀强磁场中运动时间相等,据此可画出电场强度随时间变化的关系图线如图。
同课章节目录
