4.3.1等比数列的概念(教案)-高中数学人教A版(2019)选择性必修第二册
文档属性
| 名称 | 4.3.1等比数列的概念(教案)-高中数学人教A版(2019)选择性必修第二册 |

|
|
| 格式 | docx | ||
| 文件大小 | 403.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-08 21:58:03 | ||
图片预览


文档简介
第四章
数列
4.3.1等比数列的概念
教学设计
一、教学目标
1.通过实例,理解等比数列的概念和通项公式的意义,了解等比中项的概念.
2.掌握等比数列的通项公式,能运用公式解决相关问题.
3.体会等比数列与指数函数的关系.
4.通过等比数列的概念、通项公式认识等比数列的性质,能够运用等比数列的性质解决有关问题.
二、教学重难点
1、教学重点
等比中项、等比数列的通项公式、等比数列的性质及应用.
2、教学难点
等比数列的运算、等比数列的性质及应用.
三、教学过程
1、新课导入
前面我们学习了等差数列的相关知识,那么还有什么数列是值得研究的呢?类比等差数列的研究思路和方法,这节课就来学习一下等比数列的相关知识.
2、探索新知
一、等比数列的概念
一般地,如果一个数列从第2项起,每一项与它的前一项的比都等于同一个常数,那么这个数列叫做等比数列,这个常数叫做等比数列的公比,公比通常用字母q表示(显然).
二、等比中项
如果在a与b中间插入一个数G,使a,G,b成等比数列,那么G叫做a与b的等比中项.
此时,.
三、等比数列的通项公式
设一个等比数列的公比为q,根据等比数列的定义,可得.
所以,,,……
由此可得,又,这就是说,当时上式也成立.
因此,首项为,公比为q的等比数列的通项公式为.
四、等比数列与指数函数的关系
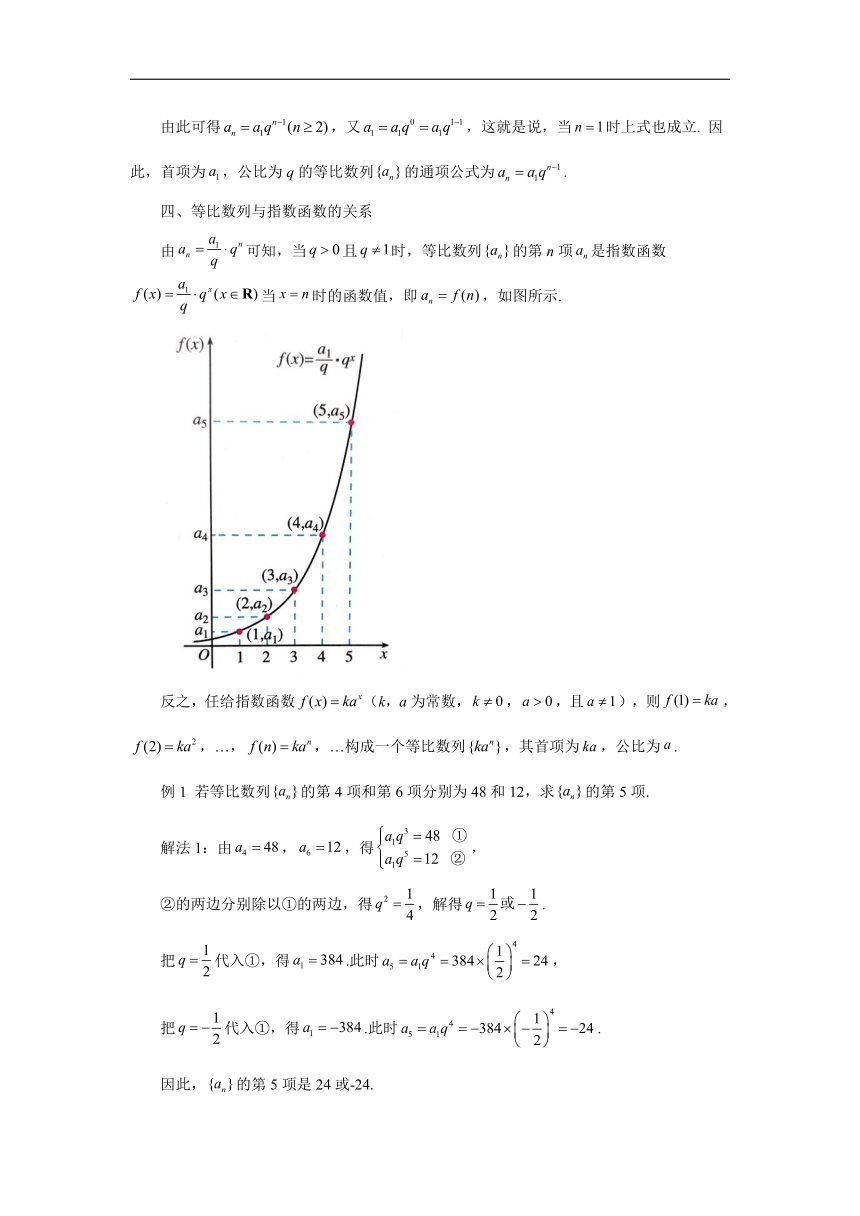
由可知,当且时,等比数列的第n项是指数函数当时的函数值,即,如图所示.
反之,任给指数函数(k,a为常数,,,且),则,,…,,…构成一个等比数列,其首项为,公比为.
例1
若等比数列的第4项和第6项分别为48和12,求的第5项.
解法1:由,,得,
②的两边分别除以①的两边,得,解得.
把代入①,得.此时,
把代入①,得.此时.
因此,的第5项是24或-24.
解法2:因为是与的等比中项,所以.
所以.
因此,的第5项是24或-24.
例2
已知等比数列的公比为,试用的第项表示.
解:由题意得①,②,
②的两边分别除以①的两边,得,
所以.
例3
数列共有5项,前三项成等比数列,后三项成等差数列,第3项等于80,第2项与第4项的和等于136,第1项与第5项的和等于132.
求这个数列.
解:设前三项的公比为,后三项的公差为,则数列的各项依次为,,80,,.
于是得,
解方程组,得或.
所以这个数列是20,40,80,96,112,或180,120,80,16,-48.
例4
用10000元购买某个理财产品一年.
(1)若以月利率0.400%的复利计息,12个月能获得多少利息(精确到1元)?
(2)若以季度复利计息,存4个季度,则当每季度利率为多少时,按季结算的利息不少于按月结算的利息(精确到)?
分析:复利是指把前一期的利息与本金之和算作本金,再计算下一期的利息,所以若原始本金为a元,每期的利率为r,则从第一期开始,各期的本利和a,,,…构成等比数列.
解:(1)设这笔钱存n个月以后的本利和组成一个数列,则是等比数列,
首项,公比,
所以.
所以12个月后的利息为(元).
(2)设季度利率为r,这笔钱存n个季度以后的本利和组成一个数列,
则也是一个等比数列,首项,公比为1+r.
于是.
因此,以季度复利计息,存4个季度后的利息为元.
解不等式,得.
所以,当季度利率不小于1.206%时,按季结算的利息不少于按月结算的利息.
例5
已知数列的首项.
(1)若为等差数列,公差,证明数列为等比数列;
(2)若为等比数列,公比,证明数列为等差数列.
证明:(1)由,,得的通项公式为.
设,则.
又,
所以是以27为首项,9为公比的等比数列.
(2)由,,得.
两边取以3为底的对数,得.
所以.
又,
所以是首项为1,公差为-2的等差数列.
例6
某工厂去年12月试产1050个高新电子产品,产品合格率为90%,从今年1月开始,工厂在接下来的两年中将生产这款产品,1月按去年12月的产量和产品合格率生产.以后每月的产量都在前一个月的基础上提高5%,产品合格率比前一个月增加0.4%,那么生产该产品一年后,月不合格品的数量能否控制在100个以内?
分析:设从今年1月起,各月的产量及不合格率分别构成数列,,则各月不合格品的数量构成数列,由题意可知,数列是等比数列,是等差数列,由于数列既非等差数列又非等比数列,所以可以先列表观察规律,再寻求问题的解决方法.
解:设从今年1月起,各月的产量及不合格率分别构成数列,.
由题意知,,
,其中,
则从今年1月起,各月不合格产品的数量是
,
由计算工具计算(精确到0.1)并列表如下.
n
1
2
3
4
5
6
7
105.0
105.8
106.5
107.0
107.2
107.2
106.9
n
8
9
10
11
12
13
14
106.4
105.5
104.2
102.6
100.6
98.1
95.0
观察发现,数列先递增,在第6项以后递减,所以只要设法证明当时,递减,且即可.
由,得,
所以当时,递减.
又,所以当时,.
所以生产该产品一年后,月不合格品的数量能控制在100个以内.
应用等比数列通项公式解实际应用问题的步骤
(1)构建等比数列模型;
(2)明确,,,等基本量;
(3)利用求解;
(4)还原为实际问题.
3、课堂练习
1.实数数列1,a,16为等比数列,则(
)
A.
B.4
C.2
D.或4
答案:D
解析:由等比中项性质得,所以.故选D.
2.已知等比数列满足,,则(
)
A.21
B.42
C.63
D.84
答案:B
解析:设等比数列的公比为,则,又因为,所以,解得,所以,故选B.
3.在等差数列中,,如果是与的等比中项,那么____________.
答案:9
解析:设等差数列的公差为d,由题意得,,又是与的等比中项,,即,,解得或(舍去).
4.已知数列满足,,数列满足,则数列的通项公式为___________.
答案:
解析:,,即,,且,,则,又,数列是首项为,公比为3的等比数列,.
4、小结作业
小结:本节课学习了等比数列的概念、等比中项、等比数列的通项公式、等比数列的性质及其应用.
作业:完成本节课课后习题.
四、板书设计
4.3.1等比数列的概念
1.等比数列的概念:一般地,如果一个数列从第2项起,每一项与它的前一项的比都等于同一个常数,那么这个数列叫做等比数列,这个常数叫做等比数列的公比,公比通常用字母q表示(显然).
2.等比中项:如果在a与b中间插入一个数G,使a,G,b成等比数列,那么G叫做a与b的等比中项.
此时,.
3.等比数列的通项公式:首项为,公比为q的等比数列的通项公式为.
数列
4.3.1等比数列的概念
教学设计
一、教学目标
1.通过实例,理解等比数列的概念和通项公式的意义,了解等比中项的概念.
2.掌握等比数列的通项公式,能运用公式解决相关问题.
3.体会等比数列与指数函数的关系.
4.通过等比数列的概念、通项公式认识等比数列的性质,能够运用等比数列的性质解决有关问题.
二、教学重难点
1、教学重点
等比中项、等比数列的通项公式、等比数列的性质及应用.
2、教学难点
等比数列的运算、等比数列的性质及应用.
三、教学过程
1、新课导入
前面我们学习了等差数列的相关知识,那么还有什么数列是值得研究的呢?类比等差数列的研究思路和方法,这节课就来学习一下等比数列的相关知识.
2、探索新知
一、等比数列的概念
一般地,如果一个数列从第2项起,每一项与它的前一项的比都等于同一个常数,那么这个数列叫做等比数列,这个常数叫做等比数列的公比,公比通常用字母q表示(显然).
二、等比中项
如果在a与b中间插入一个数G,使a,G,b成等比数列,那么G叫做a与b的等比中项.
此时,.
三、等比数列的通项公式
设一个等比数列的公比为q,根据等比数列的定义,可得.
所以,,,……
由此可得,又,这就是说,当时上式也成立.
因此,首项为,公比为q的等比数列的通项公式为.
四、等比数列与指数函数的关系
由可知,当且时,等比数列的第n项是指数函数当时的函数值,即,如图所示.
反之,任给指数函数(k,a为常数,,,且),则,,…,,…构成一个等比数列,其首项为,公比为.
例1
若等比数列的第4项和第6项分别为48和12,求的第5项.
解法1:由,,得,
②的两边分别除以①的两边,得,解得.
把代入①,得.此时,
把代入①,得.此时.
因此,的第5项是24或-24.
解法2:因为是与的等比中项,所以.
所以.
因此,的第5项是24或-24.
例2
已知等比数列的公比为,试用的第项表示.
解:由题意得①,②,
②的两边分别除以①的两边,得,
所以.
例3
数列共有5项,前三项成等比数列,后三项成等差数列,第3项等于80,第2项与第4项的和等于136,第1项与第5项的和等于132.
求这个数列.
解:设前三项的公比为,后三项的公差为,则数列的各项依次为,,80,,.
于是得,
解方程组,得或.
所以这个数列是20,40,80,96,112,或180,120,80,16,-48.
例4
用10000元购买某个理财产品一年.
(1)若以月利率0.400%的复利计息,12个月能获得多少利息(精确到1元)?
(2)若以季度复利计息,存4个季度,则当每季度利率为多少时,按季结算的利息不少于按月结算的利息(精确到)?
分析:复利是指把前一期的利息与本金之和算作本金,再计算下一期的利息,所以若原始本金为a元,每期的利率为r,则从第一期开始,各期的本利和a,,,…构成等比数列.
解:(1)设这笔钱存n个月以后的本利和组成一个数列,则是等比数列,
首项,公比,
所以.
所以12个月后的利息为(元).
(2)设季度利率为r,这笔钱存n个季度以后的本利和组成一个数列,
则也是一个等比数列,首项,公比为1+r.
于是.
因此,以季度复利计息,存4个季度后的利息为元.
解不等式,得.
所以,当季度利率不小于1.206%时,按季结算的利息不少于按月结算的利息.
例5
已知数列的首项.
(1)若为等差数列,公差,证明数列为等比数列;
(2)若为等比数列,公比,证明数列为等差数列.
证明:(1)由,,得的通项公式为.
设,则.
又,
所以是以27为首项,9为公比的等比数列.
(2)由,,得.
两边取以3为底的对数,得.
所以.
又,
所以是首项为1,公差为-2的等差数列.
例6
某工厂去年12月试产1050个高新电子产品,产品合格率为90%,从今年1月开始,工厂在接下来的两年中将生产这款产品,1月按去年12月的产量和产品合格率生产.以后每月的产量都在前一个月的基础上提高5%,产品合格率比前一个月增加0.4%,那么生产该产品一年后,月不合格品的数量能否控制在100个以内?
分析:设从今年1月起,各月的产量及不合格率分别构成数列,,则各月不合格品的数量构成数列,由题意可知,数列是等比数列,是等差数列,由于数列既非等差数列又非等比数列,所以可以先列表观察规律,再寻求问题的解决方法.
解:设从今年1月起,各月的产量及不合格率分别构成数列,.
由题意知,,
,其中,
则从今年1月起,各月不合格产品的数量是
,
由计算工具计算(精确到0.1)并列表如下.
n
1
2
3
4
5
6
7
105.0
105.8
106.5
107.0
107.2
107.2
106.9
n
8
9
10
11
12
13
14
106.4
105.5
104.2
102.6
100.6
98.1
95.0
观察发现,数列先递增,在第6项以后递减,所以只要设法证明当时,递减,且即可.
由,得,
所以当时,递减.
又,所以当时,.
所以生产该产品一年后,月不合格品的数量能控制在100个以内.
应用等比数列通项公式解实际应用问题的步骤
(1)构建等比数列模型;
(2)明确,,,等基本量;
(3)利用求解;
(4)还原为实际问题.
3、课堂练习
1.实数数列1,a,16为等比数列,则(
)
A.
B.4
C.2
D.或4
答案:D
解析:由等比中项性质得,所以.故选D.
2.已知等比数列满足,,则(
)
A.21
B.42
C.63
D.84
答案:B
解析:设等比数列的公比为,则,又因为,所以,解得,所以,故选B.
3.在等差数列中,,如果是与的等比中项,那么____________.
答案:9
解析:设等差数列的公差为d,由题意得,,又是与的等比中项,,即,,解得或(舍去).
4.已知数列满足,,数列满足,则数列的通项公式为___________.
答案:
解析:,,即,,且,,则,又,数列是首项为,公比为3的等比数列,.
4、小结作业
小结:本节课学习了等比数列的概念、等比中项、等比数列的通项公式、等比数列的性质及其应用.
作业:完成本节课课后习题.
四、板书设计
4.3.1等比数列的概念
1.等比数列的概念:一般地,如果一个数列从第2项起,每一项与它的前一项的比都等于同一个常数,那么这个数列叫做等比数列,这个常数叫做等比数列的公比,公比通常用字母q表示(显然).
2.等比中项:如果在a与b中间插入一个数G,使a,G,b成等比数列,那么G叫做a与b的等比中项.
此时,.
3.等比数列的通项公式:首项为,公比为q的等比数列的通项公式为.
