重庆名校2021-2022学年高一上学期入学诊断考试数学试题 (Word版,含答案)
文档属性
| 名称 | 重庆名校2021-2022学年高一上学期入学诊断考试数学试题 (Word版,含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 951.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-06 00:00:00 | ||
图片预览



文档简介
重庆名校2021-2022学年度上期开学诊断
高2024届数学试题
尊重自己!爱护复旦!复旦过去的光荣,将来的灿烂,全赖我们共同爱护,共同发展!同学:今天在考试的时候,不要忘记自己!不要忘记复旦!考场秩序井然,人人洁身自爱。
本试卷分为I卷和Ⅱ卷,考试时间120分钟,满分150分。请将答案工整地书写在答题卡上
第I卷(选择题)
一、单选题(本大题共12个小题,每小题4分,共48分)
1.实数2021的相反数是(
)
A.2021
B.
C.
D.
2.据国家航天局消息,航天科技集团所研制的天问一号探测器由长征五号运载火箭发射,并成功着陆于火星预选着陆区,距离地球约320000000千米.其中320000000用科学记数法表示为( )
A.
B.
C.
D.
3.下列计算正确的是( )
A.
B.
C.
D.
4.不等式组的解集在数轴上表示正确的是( )
A.
B.
C.
D.
5.计算(
)
A.
B.
C.
D.
6.多项式的一个因式为(
)
A.
B.
C.
D.
7.为执行国家药品降价政策,给人民群众带来实惠,某药品经过两次降价,每瓶零售价由100元降为64元,求平均每次降价的百分率.设平均每次降价的百分率为x,可列方程得( )
A.
B.
C.
D.
8.如图,为⊙O的直径,弦于点E,直线l切⊙O于点C,延长交l于点F,若,,则的长度为( )
A.2
B.
C.
D.4
9.已知一个直角三角形的两条直角边长恰好是方程的两根,则这个直角三角形的斜边长为(
)
A.
B.
C.
D.
10.已知函数,当时,函数的最大值为,最小值为,则实数的取值范围是(
)
A.
B.
C.
D.
11.关于的分式方程的解为正数,且使关于的一元一次不等式组
有解,则所有满足条件的整数的值之和为(
)
A.-2
B.-3
C.-4
D.-5
12.已知函数,当时,则因变量的取值范围是(
)
A.
B.
C.
D.
第II卷(非选择题)
二、填空题(本大题共8个小题,每小题4分,共32分)
13.在平面直角坐标系中,把点向右平移5个单位得到点,则点的坐标为____.
14.若二次根式有意义,则x的取值范围用区间表示为___.
15.“共和国勋章”获得者、“杂交水稻之父”袁隆平为世界粮食安全作出了杰出贡献.全球共有40多个国家引种杂交水稻,中国境外种植面积达800万公顷.某村引进了甲、乙两种超级杂交水稻品种,在条件(肥力、日照、通风……)不同的6块试验田中同时播种并核定亩产,统计结果为:/亩,﹐/亩,,则______品种更适合在该村推广.(填“甲”或“乙”)
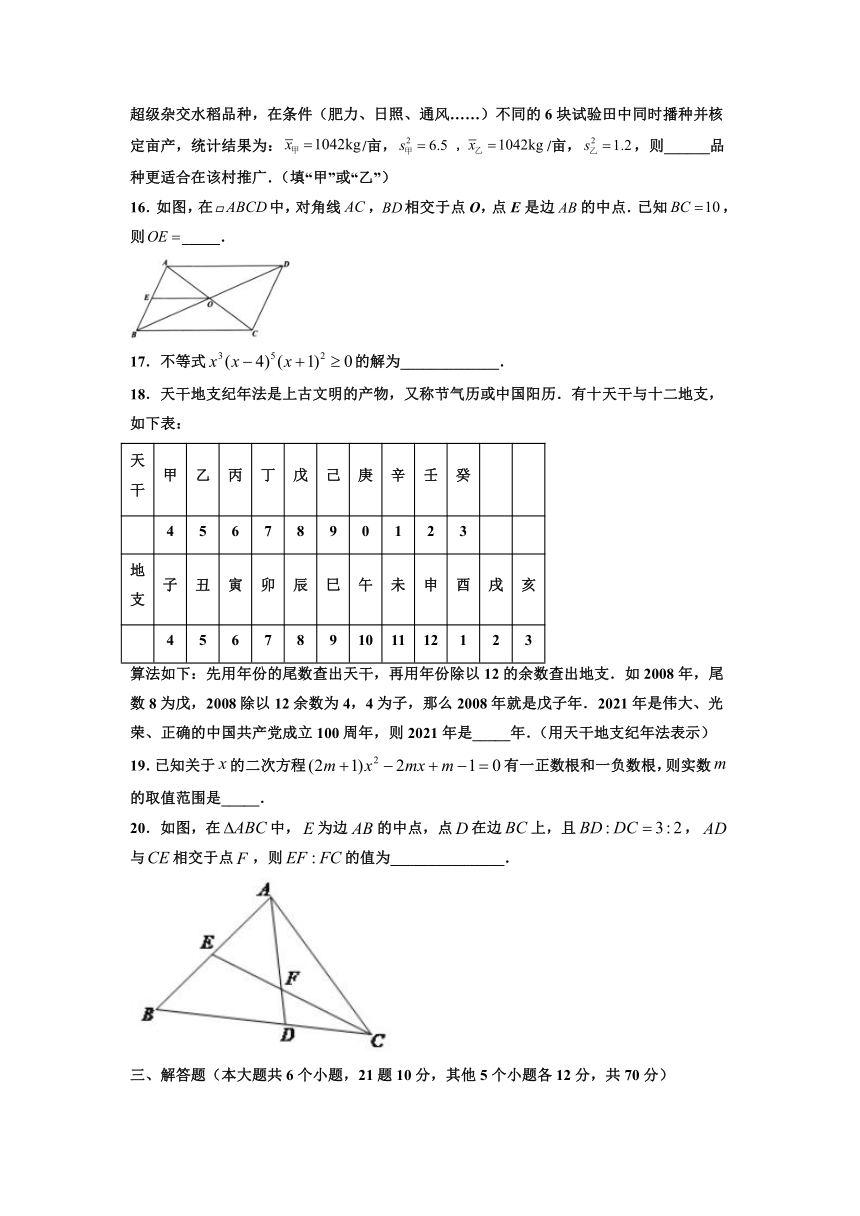
16.如图,在中,对角线,相交于点O,点E是边的中点.已知,则_____.
17.不等式的解为_____________.
18.天干地支纪年法是上古文明的产物,又称节气历或中国阳历.有十天干与十二地支,如下表:
天干
甲
乙
丙
丁
戊
己
庚
辛
壬
癸
4
5
6
7
8
9
0
1
2
3
地支
子
丑
寅
卯
辰
巳
午
未
申
酉
戌
亥
4
5
6
7
8
9
10
11
12
1
2
3
算法如下:先用年份的尾数查出天干,再用年份除以12的余数查出地支.如2008年,尾数8为戊,2008除以12余数为4,4为子,那么2008年就是戊子年.2021年是伟大、光荣、正确的中国共产党成立100周年,则2021年是_____年.(用天干地支纪年法表示)
19.已知关于的二次方程有一正数根和一负数根,则实数的取值范围是_____.
20.如图,在中,为边的中点,点在边上,且,与相交于点,则的值为_______________.
三、解答题(本大题共6个小题,21题10分,其他5个小题各12分,共70分)
21.先化简,再求值:,其中.
22.如图,矩形中点E为边上一点,将沿AE翻折后,点B恰好落在对角线的中点F上.
23.“共和国勋章”获得者钟南山院士说:按照疫苗保护率达到70%计算,中国的新冠疫苗覆盖率需要达到近80%,才有可能形成群体免疫,本着自愿的原则,18至60周岁符合身体条件的中国公民均可免费接种新冠疫苗.居民甲、乙准备接种疫苗,其居住地及工作单位附近有两个大型医院和两个社区卫生服务中心均可免费接种疫苗,提供疫苗种类如下表:
接种地点
疫苗种类
医院
A
新冠病毒灭活疫苗
B
重组新冠病毒疫苗(CHO细胞)
社区卫生服务中心
C
新冠病毒灭活疫苗
D
重组新冠病毒疫苗(CHO细胞)
若居民甲、乙均在A、B、C、D中随机独立选取一个接种点接种疫苗,且选择每个接种点的机会均等(提示:用A、B、C、D表示选取结果)
(1)求居民甲接种的是新冠病毒灭活疫苗的概率;
(2)请用列表或画树状图的方法求居民甲、乙接种的是相同种类疫苗的概率.
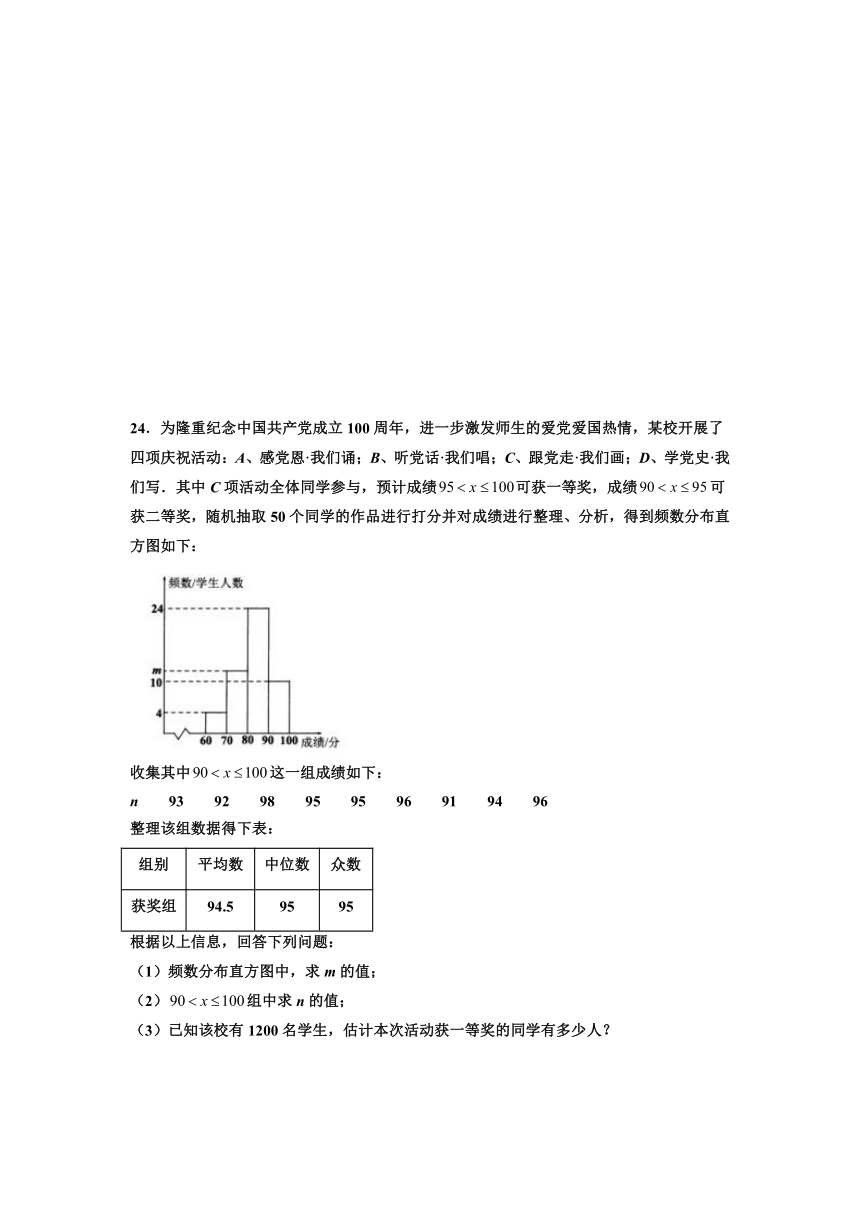
24.为隆重纪念中国共产党成立100周年,进一步激发师生的爱党爱国热情,某校开展了四项庆祝活动:A、感党恩·我们诵;B、听党话·我们唱;C、跟党走·我们画;D、学党史·我们写.其中C项活动全体同学参与,预计成绩可获一等奖,成绩可获二等奖,随机抽取50个同学的作品进行打分并对成绩进行整理、分析,得到频数分布直方图如下:
收集其中这一组成绩如下:
n
93
92
98
95
95
96
91
94
96
整理该组数据得下表:
组别
平均数
中位数
众数
获奖组
94.5
95
95
根据以上信息,回答下列问题:
(1)频数分布直方图中,求m的值;
(2)组中求n的值;
(3)已知该校有1200名学生,估计本次活动获一等奖的同学有多少人?
25.如图,点在反比例函数的图象上,轴,且交y轴于点C,交反比例函数于点B,已知.
(1)求直线的解析式;
(2)求反比例函数的解析式;
(3)点D为反比例函数上一动点,连接交y轴于点E,当E为中点时,求的面积.
26.如图,一次函数图象与坐标轴交于点A、B,二次函数图象过A、B两点.
(1)求二次函数解析式;
(2)点B关于抛物线对称轴的对称点为点C,点P是对称轴上一动点,在抛物线上是否存在点Q,使得以B、C、P、Q为顶点的四边形是菱形?若存在,求出Q点坐标;若不存在,请说明理由.
重庆名校2021-2022学年度上期开学诊断
高2024届数学试题
尊重自己!爱护复旦!复旦过去的光荣,将来的灿烂,全赖我们共同爱护,共同发展!同学:今天在考试的时候,不要忘记自己!不要忘记复旦!考场秩序井然,人人洁身自爱。
本试卷分为I卷和Ⅱ卷,考试时间120分钟,满分150分。请将答案工整地书写在答题卡上
第I卷(选择题)
一、单选题(本大题共12个小题,每小题4分,共48分)
1.实数2021的相反数是(B
)
A.2021
B.
C.
D.
2.据国家航天局消息,航天科技集团所研制的天问一号探测器由长征五号运载火箭发射,并成功着陆于火星预选着陆区,距离地球约320000000千米.其中320000000用科学记数法表示为( B )
A.
B.
C.
D.
3.下列计算正确的是( A )
A.
B.
C.
D.
4.不等式组的解集在数轴上表示正确的是( D )
A.
B.
C.
D.
5.计算(
C
)
A.
B.
C.
D.
6.多项式的一个因式为(
B
)
A.
B.
C.
D.
7.为执行国家药品降价政策,给人民群众带来实惠,某药品经过两次降价,每瓶零售价由100元降为64元,求平均每次降价的百分率.设平均每次降价的百分率为x,可列方程得( A )
A.
B.
C.
D.
8.如图,为⊙O的直径,弦于点E,直线l切⊙O于点C,延长交l于点F,若,,则的长度为( B )
A.2
B.
C.
D.4
9.已知一个直角三角形的两条直角边长恰好是方程的两根,则这个直角三角形的斜边长为(
B
)
A.
B.
C.
D.
10.已知函数,当时,函数的最大值为,最小值为,则实数的取值范围是(
A
)
A.
B.
C.
D.
11.关于的分式方程的解为正数,且使关于的一元一次不等式组
有解,则所有满足条件的整数的值之和为(
D
)
A.-2
B.-3
C.-4
D.-5
12.已知函数,当时,则因变量的取值范围是(
C
)
A.
B.
C.
D.
第II卷(非选择题)
二、填空题(本大题共8个小题,每小题4分,共32分)
13.在平面直角坐标系中,把点向右平移5个单位得到点,则点的坐标为____.
14.若二次根式有意义,则x的取值范围用区间表示为___.
15.“共和国勋章”获得者、“杂交水稻之父”袁隆平为世界粮食安全作出了杰出贡献.全球共有40多个国家引种杂交水稻,中国境外种植面积达800万公顷.某村引进了甲、乙两种超级杂交水稻品种,在条件(肥力、日照、通风……)不同的6块试验田中同时播种并核定亩产,统计结果为:/亩,﹐/亩,,则___乙___品种更适合在该村推广.(填“甲”或“乙”)
16.如图,在中,对角线,相交于点O,点E是边的中点.已知,则___5__.
17.不等式的解为_____________.
18.天干地支纪年法是上古文明的产物,又称节气历或中国阳历.有十天干与十二地支,如下表:
天干
甲
乙
丙
丁
戊
己
庚
辛
壬
癸
4
5
6
7
8
9
0
1
2
3
地支
子
丑
寅
卯
辰
巳
午
未
申
酉
戌
亥
4
5
6
7
8
9
10
11
12
1
2
3
算法如下:先用年份的尾数查出天干,再用年份除以12的余数查出地支.如2008年,尾数8为戊,2008除以12余数为4,4为子,那么2008年就是戊子年.2021年是伟大、光荣、正确的中国共产党成立100周年,则2021年是__辛丑___年.(用天干地支纪年法表示)
19.已知关于的二次方程有一正数根和一负数根,则实数的取值范围是_____.
20.如图,在中,为边的中点,点在边上,且,与相交于点,则的值为_______________.
三、解答题(本大题共6个小题,21题10分,其他5个小题各12分,共70分)
21.先化简,再求值:,其中.
解:
当时,
原式
.
22.如图,矩形中点E为边上一点,将沿AE翻折后,点B恰好落在对角线的中点F上.
(1)证明:
;
(2)若,求折痕的长度
解:(1)
矩形,
由对折可得:
为的中点,
(2),
由折叠可得:
23.“共和国勋章”获得者钟南山院士说:按照疫苗保护率达到70%计算,中国的新冠疫苗覆盖率需要达到近80%,才有可能形成群体免疫,本着自愿的原则,18至60周岁符合身体条件的中国公民均可免费接种新冠疫苗.居民甲、乙准备接种疫苗,其居住地及工作单位附近有两个大型医院和两个社区卫生服务中心均可免费接种疫苗,提供疫苗种类如下表:
接种地点
疫苗种类
医院
A
新冠病毒灭活疫苗
B
重组新冠病毒疫苗(CHO细胞)
社区卫生服务中心
C
新冠病毒灭活疫苗
D
重组新冠病毒疫苗(CHO细胞)
若居民甲、乙均在A、B、C、D中随机独立选取一个接种点接种疫苗,且选择每个接种点的机会均等(提示:用A、B、C、D表示选取结果)
(1)求居民甲接种的是新冠病毒灭活疫苗的概率;
(2)请用列表或画树状图的方法求居民甲、乙接种的是相同种类疫苗的概率.
解:(1)由概率的含义可得:
居民甲接种的是新冠病毒灭活疫苗的概率是
(2)列表如下:
由表中信息可得一共有种等可能的结果数,属于同种疫苗的结果数有:
,,,,,,,共
种,
所以居民甲、乙接种的是相同种类疫苗的概率为:
24.为隆重纪念中国共产党成立100周年,进一步激发师生的爱党爱国热情,某校开展了四项庆祝活动:A、感党恩·我们诵;B、听党话·我们唱;C、跟党走·我们画;D、学党史·我们写.其中C项活动全体同学参与,预计成绩可获一等奖,成绩可获二等奖,随机抽取50个同学的作品进行打分并对成绩进行整理、分析,得到频数分布直方图如下:
收集其中这一组成绩如下:
n
93
92
98
95
95
96
91
94
96
整理该组数据得下表:
组别
平均数
中位数
众数
获奖组
94.5
95
95
根据以上信息,回答下列问题:
(1)频数分布直方图中,求m的值;
(2)组中求n的值;
(3)已知该校有1200名学生,估计本次活动获一等奖的同学有多少人?
解:(1)m=50-4-10-24=12,
故答案为:12;
(2)90<x≤100这一组成绩如下:
n
93
92
98
95
95
96
91
94
96,其中95,96都出现了2次,
∵该组数据的众数是95,
∴n=95,
故答案为:95;
(3)抽取50个同学的作品成绩95<x≤100的人数为3,
∴1200×=72(人),
答:估计本次活动获一等奖的同学有72人.
25.如图,点在反比例函数的图象上,轴,且交y轴于点C,交反比例函数于点B,已知.
(1)求直线的解析式;
(2)求反比例函数的解析式;
(3)点D为反比例函数上一动点,连接交y轴于点E,当E为中点时,求的面积.
解:(1)
点在反比例函数的图象上,
则
设直线为:
则
所以直线为:
(2)
轴,
.
所以反比例函数为:
(3)设
而为的中点,
26.如图,一次函数图象与坐标轴交于点A、B,二次函数图象过A、B两点.
(1)求二次函数解析式;
(2)点B关于抛物线对称轴的对称点为点C,点P是对称轴上一动点,在抛物线上是否存在点Q,使得以B、C、P、Q为顶点的四边形是菱形?若存在,求出Q点坐标;若不存在,请说明理由.
解:(1)对于:当x=0时,;
当y=0时,,妥得,x=3
∴A(3,0),B(0,)
把A(3,0),B(0,)代入得:
解得,
∴抛物线的解析式为:;
(2)抛物线的对称轴为直线
故设P(1,p),Q(m,n)
①当BC为菱形对角线时,如图,
∵B,C关于对称没对称,且对称轴与x轴垂直,
∴∴BC与对称轴垂直,且BC//x轴
∵在菱形BQCP中,BC⊥PQ
∴PQ⊥x轴
∵点P在x=1上,
∴点Q也在x=1上,
当x=1时,
∴Q(1,);
②当BC为菱形一边时,若点Q在点P右侧时,如图,
∴BC//PQ,且BC=PQ
∵BC//x轴,
∴令,则有
解得,
∴
∴PQ=BC=2
∵
∴PB=BC=2
∴迠P在x轴上,
∴P(1,0)
∴Q(3,0);
若点Q在点P的左侧,如图,
同理可得,Q(-1,0)
综上所述,Q点坐标为(1,)或(3,0)或(-1,0)
高2024届数学试题
尊重自己!爱护复旦!复旦过去的光荣,将来的灿烂,全赖我们共同爱护,共同发展!同学:今天在考试的时候,不要忘记自己!不要忘记复旦!考场秩序井然,人人洁身自爱。
本试卷分为I卷和Ⅱ卷,考试时间120分钟,满分150分。请将答案工整地书写在答题卡上
第I卷(选择题)
一、单选题(本大题共12个小题,每小题4分,共48分)
1.实数2021的相反数是(
)
A.2021
B.
C.
D.
2.据国家航天局消息,航天科技集团所研制的天问一号探测器由长征五号运载火箭发射,并成功着陆于火星预选着陆区,距离地球约320000000千米.其中320000000用科学记数法表示为( )
A.
B.
C.
D.
3.下列计算正确的是( )
A.
B.
C.
D.
4.不等式组的解集在数轴上表示正确的是( )
A.
B.
C.
D.
5.计算(
)
A.
B.
C.
D.
6.多项式的一个因式为(
)
A.
B.
C.
D.
7.为执行国家药品降价政策,给人民群众带来实惠,某药品经过两次降价,每瓶零售价由100元降为64元,求平均每次降价的百分率.设平均每次降价的百分率为x,可列方程得( )
A.
B.
C.
D.
8.如图,为⊙O的直径,弦于点E,直线l切⊙O于点C,延长交l于点F,若,,则的长度为( )
A.2
B.
C.
D.4
9.已知一个直角三角形的两条直角边长恰好是方程的两根,则这个直角三角形的斜边长为(
)
A.
B.
C.
D.
10.已知函数,当时,函数的最大值为,最小值为,则实数的取值范围是(
)
A.
B.
C.
D.
11.关于的分式方程的解为正数,且使关于的一元一次不等式组
有解,则所有满足条件的整数的值之和为(
)
A.-2
B.-3
C.-4
D.-5
12.已知函数,当时,则因变量的取值范围是(
)
A.
B.
C.
D.
第II卷(非选择题)
二、填空题(本大题共8个小题,每小题4分,共32分)
13.在平面直角坐标系中,把点向右平移5个单位得到点,则点的坐标为____.
14.若二次根式有意义,则x的取值范围用区间表示为___.
15.“共和国勋章”获得者、“杂交水稻之父”袁隆平为世界粮食安全作出了杰出贡献.全球共有40多个国家引种杂交水稻,中国境外种植面积达800万公顷.某村引进了甲、乙两种超级杂交水稻品种,在条件(肥力、日照、通风……)不同的6块试验田中同时播种并核定亩产,统计结果为:/亩,﹐/亩,,则______品种更适合在该村推广.(填“甲”或“乙”)
16.如图,在中,对角线,相交于点O,点E是边的中点.已知,则_____.
17.不等式的解为_____________.
18.天干地支纪年法是上古文明的产物,又称节气历或中国阳历.有十天干与十二地支,如下表:
天干
甲
乙
丙
丁
戊
己
庚
辛
壬
癸
4
5
6
7
8
9
0
1
2
3
地支
子
丑
寅
卯
辰
巳
午
未
申
酉
戌
亥
4
5
6
7
8
9
10
11
12
1
2
3
算法如下:先用年份的尾数查出天干,再用年份除以12的余数查出地支.如2008年,尾数8为戊,2008除以12余数为4,4为子,那么2008年就是戊子年.2021年是伟大、光荣、正确的中国共产党成立100周年,则2021年是_____年.(用天干地支纪年法表示)
19.已知关于的二次方程有一正数根和一负数根,则实数的取值范围是_____.
20.如图,在中,为边的中点,点在边上,且,与相交于点,则的值为_______________.
三、解答题(本大题共6个小题,21题10分,其他5个小题各12分,共70分)
21.先化简,再求值:,其中.
22.如图,矩形中点E为边上一点,将沿AE翻折后,点B恰好落在对角线的中点F上.
23.“共和国勋章”获得者钟南山院士说:按照疫苗保护率达到70%计算,中国的新冠疫苗覆盖率需要达到近80%,才有可能形成群体免疫,本着自愿的原则,18至60周岁符合身体条件的中国公民均可免费接种新冠疫苗.居民甲、乙准备接种疫苗,其居住地及工作单位附近有两个大型医院和两个社区卫生服务中心均可免费接种疫苗,提供疫苗种类如下表:
接种地点
疫苗种类
医院
A
新冠病毒灭活疫苗
B
重组新冠病毒疫苗(CHO细胞)
社区卫生服务中心
C
新冠病毒灭活疫苗
D
重组新冠病毒疫苗(CHO细胞)
若居民甲、乙均在A、B、C、D中随机独立选取一个接种点接种疫苗,且选择每个接种点的机会均等(提示:用A、B、C、D表示选取结果)
(1)求居民甲接种的是新冠病毒灭活疫苗的概率;
(2)请用列表或画树状图的方法求居民甲、乙接种的是相同种类疫苗的概率.
24.为隆重纪念中国共产党成立100周年,进一步激发师生的爱党爱国热情,某校开展了四项庆祝活动:A、感党恩·我们诵;B、听党话·我们唱;C、跟党走·我们画;D、学党史·我们写.其中C项活动全体同学参与,预计成绩可获一等奖,成绩可获二等奖,随机抽取50个同学的作品进行打分并对成绩进行整理、分析,得到频数分布直方图如下:
收集其中这一组成绩如下:
n
93
92
98
95
95
96
91
94
96
整理该组数据得下表:
组别
平均数
中位数
众数
获奖组
94.5
95
95
根据以上信息,回答下列问题:
(1)频数分布直方图中,求m的值;
(2)组中求n的值;
(3)已知该校有1200名学生,估计本次活动获一等奖的同学有多少人?
25.如图,点在反比例函数的图象上,轴,且交y轴于点C,交反比例函数于点B,已知.
(1)求直线的解析式;
(2)求反比例函数的解析式;
(3)点D为反比例函数上一动点,连接交y轴于点E,当E为中点时,求的面积.
26.如图,一次函数图象与坐标轴交于点A、B,二次函数图象过A、B两点.
(1)求二次函数解析式;
(2)点B关于抛物线对称轴的对称点为点C,点P是对称轴上一动点,在抛物线上是否存在点Q,使得以B、C、P、Q为顶点的四边形是菱形?若存在,求出Q点坐标;若不存在,请说明理由.
重庆名校2021-2022学年度上期开学诊断
高2024届数学试题
尊重自己!爱护复旦!复旦过去的光荣,将来的灿烂,全赖我们共同爱护,共同发展!同学:今天在考试的时候,不要忘记自己!不要忘记复旦!考场秩序井然,人人洁身自爱。
本试卷分为I卷和Ⅱ卷,考试时间120分钟,满分150分。请将答案工整地书写在答题卡上
第I卷(选择题)
一、单选题(本大题共12个小题,每小题4分,共48分)
1.实数2021的相反数是(B
)
A.2021
B.
C.
D.
2.据国家航天局消息,航天科技集团所研制的天问一号探测器由长征五号运载火箭发射,并成功着陆于火星预选着陆区,距离地球约320000000千米.其中320000000用科学记数法表示为( B )
A.
B.
C.
D.
3.下列计算正确的是( A )
A.
B.
C.
D.
4.不等式组的解集在数轴上表示正确的是( D )
A.
B.
C.
D.
5.计算(
C
)
A.
B.
C.
D.
6.多项式的一个因式为(
B
)
A.
B.
C.
D.
7.为执行国家药品降价政策,给人民群众带来实惠,某药品经过两次降价,每瓶零售价由100元降为64元,求平均每次降价的百分率.设平均每次降价的百分率为x,可列方程得( A )
A.
B.
C.
D.
8.如图,为⊙O的直径,弦于点E,直线l切⊙O于点C,延长交l于点F,若,,则的长度为( B )
A.2
B.
C.
D.4
9.已知一个直角三角形的两条直角边长恰好是方程的两根,则这个直角三角形的斜边长为(
B
)
A.
B.
C.
D.
10.已知函数,当时,函数的最大值为,最小值为,则实数的取值范围是(
A
)
A.
B.
C.
D.
11.关于的分式方程的解为正数,且使关于的一元一次不等式组
有解,则所有满足条件的整数的值之和为(
D
)
A.-2
B.-3
C.-4
D.-5
12.已知函数,当时,则因变量的取值范围是(
C
)
A.
B.
C.
D.
第II卷(非选择题)
二、填空题(本大题共8个小题,每小题4分,共32分)
13.在平面直角坐标系中,把点向右平移5个单位得到点,则点的坐标为____.
14.若二次根式有意义,则x的取值范围用区间表示为___.
15.“共和国勋章”获得者、“杂交水稻之父”袁隆平为世界粮食安全作出了杰出贡献.全球共有40多个国家引种杂交水稻,中国境外种植面积达800万公顷.某村引进了甲、乙两种超级杂交水稻品种,在条件(肥力、日照、通风……)不同的6块试验田中同时播种并核定亩产,统计结果为:/亩,﹐/亩,,则___乙___品种更适合在该村推广.(填“甲”或“乙”)
16.如图,在中,对角线,相交于点O,点E是边的中点.已知,则___5__.
17.不等式的解为_____________.
18.天干地支纪年法是上古文明的产物,又称节气历或中国阳历.有十天干与十二地支,如下表:
天干
甲
乙
丙
丁
戊
己
庚
辛
壬
癸
4
5
6
7
8
9
0
1
2
3
地支
子
丑
寅
卯
辰
巳
午
未
申
酉
戌
亥
4
5
6
7
8
9
10
11
12
1
2
3
算法如下:先用年份的尾数查出天干,再用年份除以12的余数查出地支.如2008年,尾数8为戊,2008除以12余数为4,4为子,那么2008年就是戊子年.2021年是伟大、光荣、正确的中国共产党成立100周年,则2021年是__辛丑___年.(用天干地支纪年法表示)
19.已知关于的二次方程有一正数根和一负数根,则实数的取值范围是_____.
20.如图,在中,为边的中点,点在边上,且,与相交于点,则的值为_______________.
三、解答题(本大题共6个小题,21题10分,其他5个小题各12分,共70分)
21.先化简,再求值:,其中.
解:
当时,
原式
.
22.如图,矩形中点E为边上一点,将沿AE翻折后,点B恰好落在对角线的中点F上.
(1)证明:
;
(2)若,求折痕的长度
解:(1)
矩形,
由对折可得:
为的中点,
(2),
由折叠可得:
23.“共和国勋章”获得者钟南山院士说:按照疫苗保护率达到70%计算,中国的新冠疫苗覆盖率需要达到近80%,才有可能形成群体免疫,本着自愿的原则,18至60周岁符合身体条件的中国公民均可免费接种新冠疫苗.居民甲、乙准备接种疫苗,其居住地及工作单位附近有两个大型医院和两个社区卫生服务中心均可免费接种疫苗,提供疫苗种类如下表:
接种地点
疫苗种类
医院
A
新冠病毒灭活疫苗
B
重组新冠病毒疫苗(CHO细胞)
社区卫生服务中心
C
新冠病毒灭活疫苗
D
重组新冠病毒疫苗(CHO细胞)
若居民甲、乙均在A、B、C、D中随机独立选取一个接种点接种疫苗,且选择每个接种点的机会均等(提示:用A、B、C、D表示选取结果)
(1)求居民甲接种的是新冠病毒灭活疫苗的概率;
(2)请用列表或画树状图的方法求居民甲、乙接种的是相同种类疫苗的概率.
解:(1)由概率的含义可得:
居民甲接种的是新冠病毒灭活疫苗的概率是
(2)列表如下:
由表中信息可得一共有种等可能的结果数,属于同种疫苗的结果数有:
,,,,,,,共
种,
所以居民甲、乙接种的是相同种类疫苗的概率为:
24.为隆重纪念中国共产党成立100周年,进一步激发师生的爱党爱国热情,某校开展了四项庆祝活动:A、感党恩·我们诵;B、听党话·我们唱;C、跟党走·我们画;D、学党史·我们写.其中C项活动全体同学参与,预计成绩可获一等奖,成绩可获二等奖,随机抽取50个同学的作品进行打分并对成绩进行整理、分析,得到频数分布直方图如下:
收集其中这一组成绩如下:
n
93
92
98
95
95
96
91
94
96
整理该组数据得下表:
组别
平均数
中位数
众数
获奖组
94.5
95
95
根据以上信息,回答下列问题:
(1)频数分布直方图中,求m的值;
(2)组中求n的值;
(3)已知该校有1200名学生,估计本次活动获一等奖的同学有多少人?
解:(1)m=50-4-10-24=12,
故答案为:12;
(2)90<x≤100这一组成绩如下:
n
93
92
98
95
95
96
91
94
96,其中95,96都出现了2次,
∵该组数据的众数是95,
∴n=95,
故答案为:95;
(3)抽取50个同学的作品成绩95<x≤100的人数为3,
∴1200×=72(人),
答:估计本次活动获一等奖的同学有72人.
25.如图,点在反比例函数的图象上,轴,且交y轴于点C,交反比例函数于点B,已知.
(1)求直线的解析式;
(2)求反比例函数的解析式;
(3)点D为反比例函数上一动点,连接交y轴于点E,当E为中点时,求的面积.
解:(1)
点在反比例函数的图象上,
则
设直线为:
则
所以直线为:
(2)
轴,
.
所以反比例函数为:
(3)设
而为的中点,
26.如图,一次函数图象与坐标轴交于点A、B,二次函数图象过A、B两点.
(1)求二次函数解析式;
(2)点B关于抛物线对称轴的对称点为点C,点P是对称轴上一动点,在抛物线上是否存在点Q,使得以B、C、P、Q为顶点的四边形是菱形?若存在,求出Q点坐标;若不存在,请说明理由.
解:(1)对于:当x=0时,;
当y=0时,,妥得,x=3
∴A(3,0),B(0,)
把A(3,0),B(0,)代入得:
解得,
∴抛物线的解析式为:;
(2)抛物线的对称轴为直线
故设P(1,p),Q(m,n)
①当BC为菱形对角线时,如图,
∵B,C关于对称没对称,且对称轴与x轴垂直,
∴∴BC与对称轴垂直,且BC//x轴
∵在菱形BQCP中,BC⊥PQ
∴PQ⊥x轴
∵点P在x=1上,
∴点Q也在x=1上,
当x=1时,
∴Q(1,);
②当BC为菱形一边时,若点Q在点P右侧时,如图,
∴BC//PQ,且BC=PQ
∵BC//x轴,
∴令,则有
解得,
∴
∴PQ=BC=2
∵
∴PB=BC=2
∴迠P在x轴上,
∴P(1,0)
∴Q(3,0);
若点Q在点P的左侧,如图,
同理可得,Q(-1,0)
综上所述,Q点坐标为(1,)或(3,0)或(-1,0)
同课章节目录
