华东师大版数学九年级上册25.2.3列举所有机会均等的结果 课件(共21张PPT)
文档属性
| 名称 | 华东师大版数学九年级上册25.2.3列举所有机会均等的结果 课件(共21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-07 00:00:00 | ||
图片预览







文档简介
(共21张PPT)
九年级数学
新课导入:
上店镇开往汝阳县有三辆班车,票价相同但车的舒适度不同,雷扬和高飞需乘车去县城,但不知道三辆车开来的顺序,两人
采用不同的乘车方案:雷扬:无论如何决定乘坐开来的第一辆车,而高飞:则先观察后上车,当第一辆车开来时,他不上车,而是仔细观察车的舒适状况,若第二辆车的状况比第一辆车好,他就上第二辆车,若第二辆不如第一辆车,他就上第三辆车。若按这三辆车的舒适度分为优、中、差三等,请你思考?
1)三辆车按出现的先后顺序共有几种可能?
2)分析那种方案乘坐优等车的可能性大?
1、会准确运用列表法、画树状图法求随机事件的概率;
2、准确根据问题中涉及的因素选择恰当的方法求随机事件的概率;
3、培养逻辑思维能力,能在复杂事件中找准解题关键点.
2.概率的计算公式是什么?
一个事件发生的可能性,就叫做该事件的概率。
一.知识准备
3.已经掌握的求随机事件概率的方法:
1.什么是概率?
关注的结果的个数m
P(事件发生)=
所有机会均等的结果的个数n
(1)理论分析的方法;
(2)在大量重复试验中,用频率估计概率.
随机掷一枚均匀的硬币两次,至少有一次正面朝上的概率是多少?
共有4种结果,并且可能性相同,而至少有一次正面朝上的结果有3种:(正,正),(正,反),(反,正),因此至少有一次正面朝上的概率是
开始
正
反
正
反
正
反
(正,正)
(正,反)
(反,正)
(反,反)
一、自主学习
解:画图如下
结果:
例4、抛掷一枚普通的硬币3次.有人说连续掷出三个正面和先掷出两个正面再掷出一个反面的机会是一样的.你同意吗?
?
开始
第一次
正
反
第二次
正
反
正
反
第三次
正
反
正
正
正
反
反
反
从上至下每一条路径就是一种可能的结
果,而且每种结果发生的机会相等.
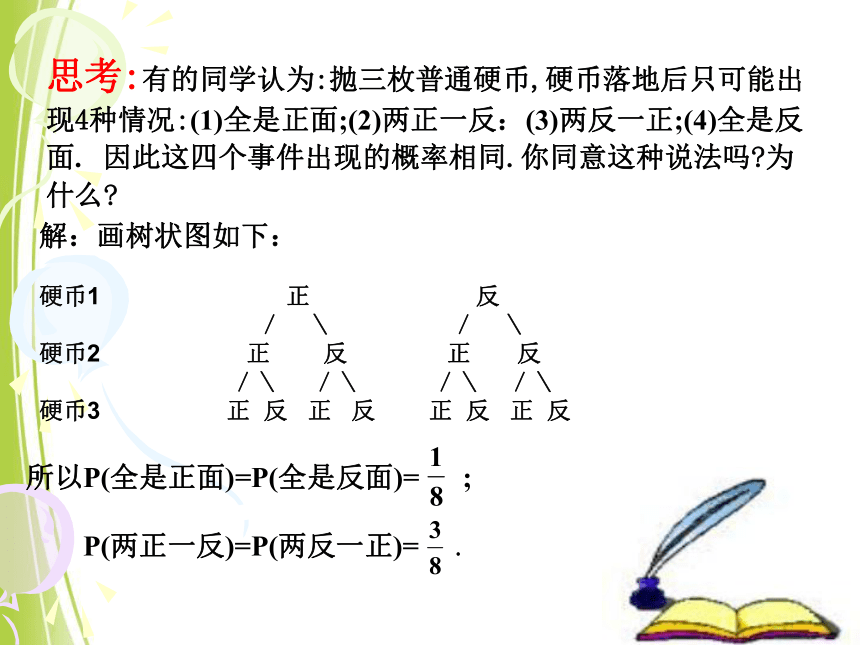
思考:有的同学认为:抛三枚普通硬币,硬币落地后只可能出现4种情况:(1)全是正面;(2)两正一反:(3)两反一正;(4)全是反面.
因此这四个事件出现的概率相同.你同意这种说法吗?为什么?
解:画树状图如下:
??????????????????????????????????????????????????????????????????????????????
硬币1????????????
?
?
正??????????????
反
??????????????????????
/?
\???????
/??
\
硬币2???????????
?正????
反????
正?????
反
???????????????????
/\??
/\??
/\??
/\
硬币3???????
?
正?
反?
正
反?
正
反?
正
反
所以P(全是正面)=P(全是反面)=
;
P(两正一反)=P(两反一正)=
.
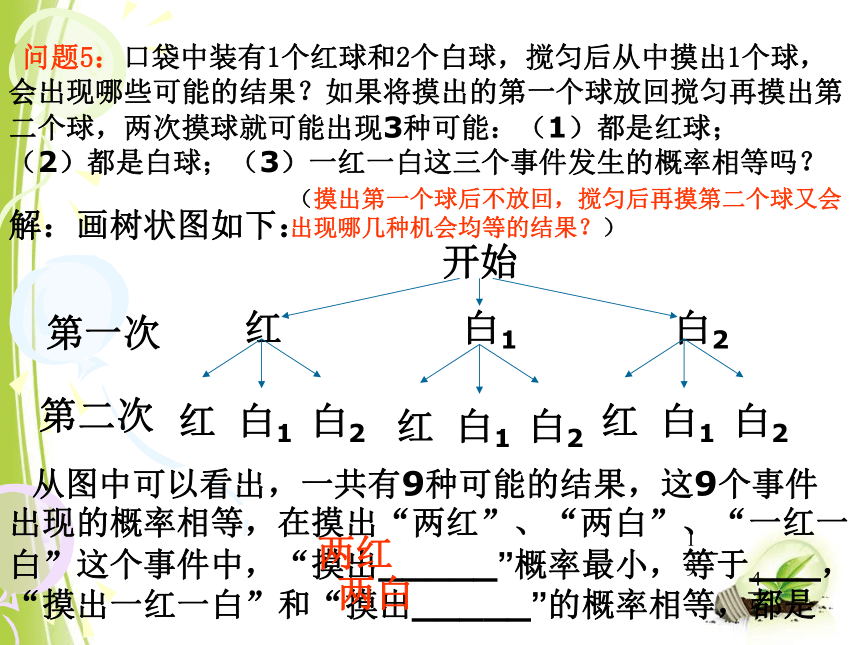
问题5:口袋中装有1个红球和2个白球,搅匀后从中摸出1个球,会出现哪些可能的结果?如果将摸出的第一个球放回搅匀再摸出第二个球,两次摸球就可能出现3种可能:(1)都是红球;
(2)都是白球;(3)一红一白这三个事件发生的概率相等吗?
白2
红
白1
白2
开始
红
白1
白2
红
白1
白2
红
白1
第一次
第二次
从图中可以看出,一共有9种可能的结果,这9个事件出现的概率相等,在摸出“两红”、“两白”、“一红一白”这个事件中,“摸出_____”概率最小,等于___,“摸出一红一白”和“摸出_____”的概率相等,都是____
两红
两白
(摸出第一个球后不放回,搅匀后再摸第二个球又会出现哪几种机会均等的结果?)
解:画树状图如下:
问题6、同时掷两个质地均匀的骰子,计算下列事件的概率:
(1)两个骰子的点数相同
(2)两个骰子的点数之和是9
(3)至少有一个骰子的点数为2
同时掷两个质地均匀的骰子,计算下列事件的概率:
(1)两个骰子的点数相同
(2)两个骰子的点数之和是9
(3)至少有一个骰子的点数为2
1
2
3
4
5
6
1
2
3
4
5
6
解:由列表得,同时掷两个骰子,可能出现的结果有36个,它们出现的可能性相等。
(1)满足两个骰子的点数相同(记为事件A)的结果有6个,则
P(A)=
=
(2)满足两个骰子的点数之和是9(记为事件B)的结果有4个,则
P(B)=
=
(3)满足至少有一个骰子的点数为2(记为事件C)的结果有11个,则
P(C)=
第
一
个
第
二
个
1,1)
2,1)
3,1
4,1)
5,1)
6,1)
1,2)
2,2)
3,2)
4,2)
5,2)
6,2)
1,3)
2,3)
3,3)
4,3)
5,3)
6,3)
1,4)
2,4)
3,4)
4,4)
5,4)
6,4)
1,5)
2,5)
3,5)
4,5)
5,5)
6,5)
1,6)
2,6)
3,6)
4,6
5,6)
6,6)
如何选用列表法或画树状图法更合适?
列表法:当一次试验涉及两个因素,并且可能出现的结果数目较多时,为不重不漏地列出所有可能的结果,通常采用列表法。
画树状图法:当一次试验涉及三个或更多的因素时,用列表法就不方便了,为不重不漏地列出所有可能的结果,通常采用画树状图法求概率。
问题7:
九(4)班将选出正、副班长各一名,现有甲、乙两位男生和丙、丁两位女生参加竞选.
请用树状图或列表法求出两位女生同时当选正、副班长的概率.
综合练习:
学有所用:
上店镇开往汝阳县有三辆班车,票价相同但车的舒适度不同,和雷扬高飞需乘车去县城,但不知道三辆车开来的顺序,两人
采用不同的乘车方案:雷扬、无论如何决定乘坐开来的第一辆车,而高飞、则先观察后上车,当第一辆车开来时,他不上车,而是仔细观察车的舒适状况,若第二辆车的状况比第一辆车好,他就上第二辆车,若第二辆不如第一辆车,他就上第三辆车。若按这三辆车的舒适度分为优、中、差三等,请你思考?
(1)三辆车按出现的先后顺序共有哪几种可能?
(2)分析
那种方案乘坐优等车的可能性大?
我与中考“零”距离:
1、(2018年8题)现有四张卡片,其中三张卡片正面是的图案是红心,一张卡片正面上的图案是梅花,它们除此之外完全相同,把这四张卡片背面朝上洗匀,从中随机抽取两张,则这两张卡片正面图案相同的概率是___
2、(2017年8题)如图是一次数学活动课制作的一个转盘,盘面被分为四个扇形区域,并分别标有数字-1、0、1、2,若转动转盘两次,每次转盘停止后记录指针区域的数字,
则记录的两个数字是正数的概率
为___
我与中考“零”距离:
3、(2016河南12题)在“阳光体育活动时间”班主任随机将全班同学分成4组进行活动,该班小明和小亮被分在同一组的概率是___
4、(2014河南13题)一个不透明的袋子中装有仅颜色不同的2个红球和两个白球,两人一次从袋子中随机摸出一个小球不放回,则第一个人摸到红球且第二个人摸到白球的概率是———
5、(2015河南13题)现有四张分别标有数字1、2、2、3的卡片,它们除数字外完全相同,把卡片背面朝上洗匀,从中随机抽取一张后放回,再洗匀从中抽取一张,则两次抽出的卡片数字不同的概率是——
1、甲乙两人投掷一枚质地均匀的正六面体骰子,用字母p、q分别表示两人各投掷一次的点数。
1)求满足关于X的方程x2+px+q=0有实数根的概率;
2)求1中方程有两个相等实数根的概率;
知识的完美结合:
2、有A、B两个不透明的布袋,A袋中有两个完全相同的小球,分别标有数字0和-2,B袋中有完全相同的三个小球,分别有数字-2、0和1,小明从A袋中随机取出一个小球,记录标有的数字为x,再从B袋中随机取出一个小球,记录标有的数字为y,这样确定了点Q的坐标(x,y).
(1)写出点Q所有可能的坐标;
(2)求出点Q在x轴上的概率。
3、小丽到外婆家过暑假,带了两件上衣(一件红色,一件绿色)和三条裙子(一条绿色,一条橙色,一条黑色),则她拿出一件上衣和一条裙子是同色的概率是多少?
4、转动下面的两个转盘各一次,将所得的数字相加,它们的和是奇数的概率是多少?
在这节课的学习中……
课堂小结
1、你学到了那些知识;
2、针对本节课在今后的学习中你觉得应该注意些什么?
3、通过今天的学习你的感受是什么……
九年级数学
新课导入:
上店镇开往汝阳县有三辆班车,票价相同但车的舒适度不同,雷扬和高飞需乘车去县城,但不知道三辆车开来的顺序,两人
采用不同的乘车方案:雷扬:无论如何决定乘坐开来的第一辆车,而高飞:则先观察后上车,当第一辆车开来时,他不上车,而是仔细观察车的舒适状况,若第二辆车的状况比第一辆车好,他就上第二辆车,若第二辆不如第一辆车,他就上第三辆车。若按这三辆车的舒适度分为优、中、差三等,请你思考?
1)三辆车按出现的先后顺序共有几种可能?
2)分析那种方案乘坐优等车的可能性大?
1、会准确运用列表法、画树状图法求随机事件的概率;
2、准确根据问题中涉及的因素选择恰当的方法求随机事件的概率;
3、培养逻辑思维能力,能在复杂事件中找准解题关键点.
2.概率的计算公式是什么?
一个事件发生的可能性,就叫做该事件的概率。
一.知识准备
3.已经掌握的求随机事件概率的方法:
1.什么是概率?
关注的结果的个数m
P(事件发生)=
所有机会均等的结果的个数n
(1)理论分析的方法;
(2)在大量重复试验中,用频率估计概率.
随机掷一枚均匀的硬币两次,至少有一次正面朝上的概率是多少?
共有4种结果,并且可能性相同,而至少有一次正面朝上的结果有3种:(正,正),(正,反),(反,正),因此至少有一次正面朝上的概率是
开始
正
反
正
反
正
反
(正,正)
(正,反)
(反,正)
(反,反)
一、自主学习
解:画图如下
结果:
例4、抛掷一枚普通的硬币3次.有人说连续掷出三个正面和先掷出两个正面再掷出一个反面的机会是一样的.你同意吗?
?
开始
第一次
正
反
第二次
正
反
正
反
第三次
正
反
正
正
正
反
反
反
从上至下每一条路径就是一种可能的结
果,而且每种结果发生的机会相等.
思考:有的同学认为:抛三枚普通硬币,硬币落地后只可能出现4种情况:(1)全是正面;(2)两正一反:(3)两反一正;(4)全是反面.
因此这四个事件出现的概率相同.你同意这种说法吗?为什么?
解:画树状图如下:
??????????????????????????????????????????????????????????????????????????????
硬币1????????????
?
?
正??????????????
反
??????????????????????
/?
\???????
/??
\
硬币2???????????
?正????
反????
正?????
反
???????????????????
/\??
/\??
/\??
/\
硬币3???????
?
正?
反?
正
反?
正
反?
正
反
所以P(全是正面)=P(全是反面)=
;
P(两正一反)=P(两反一正)=
.
问题5:口袋中装有1个红球和2个白球,搅匀后从中摸出1个球,会出现哪些可能的结果?如果将摸出的第一个球放回搅匀再摸出第二个球,两次摸球就可能出现3种可能:(1)都是红球;
(2)都是白球;(3)一红一白这三个事件发生的概率相等吗?
白2
红
白1
白2
开始
红
白1
白2
红
白1
白2
红
白1
第一次
第二次
从图中可以看出,一共有9种可能的结果,这9个事件出现的概率相等,在摸出“两红”、“两白”、“一红一白”这个事件中,“摸出_____”概率最小,等于___,“摸出一红一白”和“摸出_____”的概率相等,都是____
两红
两白
(摸出第一个球后不放回,搅匀后再摸第二个球又会出现哪几种机会均等的结果?)
解:画树状图如下:
问题6、同时掷两个质地均匀的骰子,计算下列事件的概率:
(1)两个骰子的点数相同
(2)两个骰子的点数之和是9
(3)至少有一个骰子的点数为2
同时掷两个质地均匀的骰子,计算下列事件的概率:
(1)两个骰子的点数相同
(2)两个骰子的点数之和是9
(3)至少有一个骰子的点数为2
1
2
3
4
5
6
1
2
3
4
5
6
解:由列表得,同时掷两个骰子,可能出现的结果有36个,它们出现的可能性相等。
(1)满足两个骰子的点数相同(记为事件A)的结果有6个,则
P(A)=
=
(2)满足两个骰子的点数之和是9(记为事件B)的结果有4个,则
P(B)=
=
(3)满足至少有一个骰子的点数为2(记为事件C)的结果有11个,则
P(C)=
第
一
个
第
二
个
1,1)
2,1)
3,1
4,1)
5,1)
6,1)
1,2)
2,2)
3,2)
4,2)
5,2)
6,2)
1,3)
2,3)
3,3)
4,3)
5,3)
6,3)
1,4)
2,4)
3,4)
4,4)
5,4)
6,4)
1,5)
2,5)
3,5)
4,5)
5,5)
6,5)
1,6)
2,6)
3,6)
4,6
5,6)
6,6)
如何选用列表法或画树状图法更合适?
列表法:当一次试验涉及两个因素,并且可能出现的结果数目较多时,为不重不漏地列出所有可能的结果,通常采用列表法。
画树状图法:当一次试验涉及三个或更多的因素时,用列表法就不方便了,为不重不漏地列出所有可能的结果,通常采用画树状图法求概率。
问题7:
九(4)班将选出正、副班长各一名,现有甲、乙两位男生和丙、丁两位女生参加竞选.
请用树状图或列表法求出两位女生同时当选正、副班长的概率.
综合练习:
学有所用:
上店镇开往汝阳县有三辆班车,票价相同但车的舒适度不同,和雷扬高飞需乘车去县城,但不知道三辆车开来的顺序,两人
采用不同的乘车方案:雷扬、无论如何决定乘坐开来的第一辆车,而高飞、则先观察后上车,当第一辆车开来时,他不上车,而是仔细观察车的舒适状况,若第二辆车的状况比第一辆车好,他就上第二辆车,若第二辆不如第一辆车,他就上第三辆车。若按这三辆车的舒适度分为优、中、差三等,请你思考?
(1)三辆车按出现的先后顺序共有哪几种可能?
(2)分析
那种方案乘坐优等车的可能性大?
我与中考“零”距离:
1、(2018年8题)现有四张卡片,其中三张卡片正面是的图案是红心,一张卡片正面上的图案是梅花,它们除此之外完全相同,把这四张卡片背面朝上洗匀,从中随机抽取两张,则这两张卡片正面图案相同的概率是___
2、(2017年8题)如图是一次数学活动课制作的一个转盘,盘面被分为四个扇形区域,并分别标有数字-1、0、1、2,若转动转盘两次,每次转盘停止后记录指针区域的数字,
则记录的两个数字是正数的概率
为___
我与中考“零”距离:
3、(2016河南12题)在“阳光体育活动时间”班主任随机将全班同学分成4组进行活动,该班小明和小亮被分在同一组的概率是___
4、(2014河南13题)一个不透明的袋子中装有仅颜色不同的2个红球和两个白球,两人一次从袋子中随机摸出一个小球不放回,则第一个人摸到红球且第二个人摸到白球的概率是———
5、(2015河南13题)现有四张分别标有数字1、2、2、3的卡片,它们除数字外完全相同,把卡片背面朝上洗匀,从中随机抽取一张后放回,再洗匀从中抽取一张,则两次抽出的卡片数字不同的概率是——
1、甲乙两人投掷一枚质地均匀的正六面体骰子,用字母p、q分别表示两人各投掷一次的点数。
1)求满足关于X的方程x2+px+q=0有实数根的概率;
2)求1中方程有两个相等实数根的概率;
知识的完美结合:
2、有A、B两个不透明的布袋,A袋中有两个完全相同的小球,分别标有数字0和-2,B袋中有完全相同的三个小球,分别有数字-2、0和1,小明从A袋中随机取出一个小球,记录标有的数字为x,再从B袋中随机取出一个小球,记录标有的数字为y,这样确定了点Q的坐标(x,y).
(1)写出点Q所有可能的坐标;
(2)求出点Q在x轴上的概率。
3、小丽到外婆家过暑假,带了两件上衣(一件红色,一件绿色)和三条裙子(一条绿色,一条橙色,一条黑色),则她拿出一件上衣和一条裙子是同色的概率是多少?
4、转动下面的两个转盘各一次,将所得的数字相加,它们的和是奇数的概率是多少?
在这节课的学习中……
课堂小结
1、你学到了那些知识;
2、针对本节课在今后的学习中你觉得应该注意些什么?
3、通过今天的学习你的感受是什么……
