广东省徐闻一高2022届高三上学期月考(一)数学试题 (Word版,含答案)
文档属性
| 名称 | 广东省徐闻一高2022届高三上学期月考(一)数学试题 (Word版,含答案) | 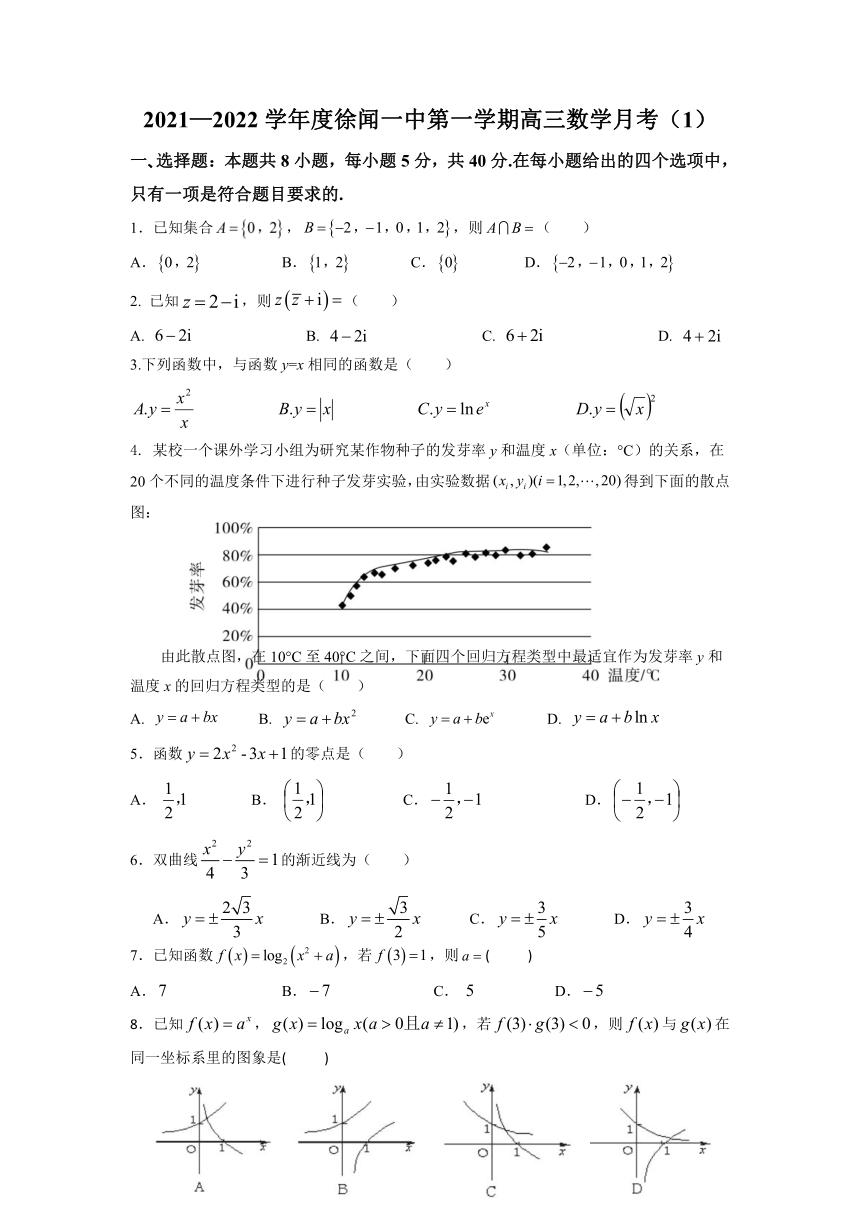 | |
| 格式 | doc | ||
| 文件大小 | 656.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-06 14:49:36 | ||
图片预览




文档简介
2021—2022学年度徐闻一中第一学期高三数学月考(1)
一?选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知集合,,则(
)
A.
B.
C.
D.
2.
已知,则(
)
A.
B.
C.
D.
3.下列函数中,与函数y=x相同的函数是(
)
某校一个课外学习小组为研究某作物种子的发芽率y和温度x(单位:°C)的关系,在20个不同的温度条件下进行种子发芽实验,由实验数据得到下面的散点图:
由此散点图,在10°C至40°C之间,下面四个回归方程类型中最适宜作为发芽率y和温度x的回归方程类型的是(
)
A.
B.
C.
D.
5.函数的零点是(
)
A.
B.
C.
D.
6.双曲线的渐近线为(
)
A.
B. C.
D.
7.已知函数,若,则(
)
A.
B.
C.
D.
8.已知,,若,则与在同一坐标系里的图象是(
)
二?选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.
9.下列表述正确的是:(
)
“”是“”的充分不必要条件
设向量,若,则
已知,满足,则
“”的否定是“”
11.下列命题为真命题的是(
)
12.已知点在圆上,点、,则(
)
A.
点到直线的距离小于
B.
点到直线的距离大于
C.
当最小时,
D.
当最大时,
三?填空题:本题共4小题,每小题5分,共20分.
13.函数的定义域为________________
14.函数,若,则_______________
15.设函数.若为奇函数,则曲线在点处的切线方程为______________________
16.函数的最小值为______.
四?解答题:本题共6小题,共70分.解答应写出文字说明?证明过程或演算步骤.
17.(本小题满分10分)已知等差数列的前项和为,,.
(1)求的通项公式;
(2)设,记为数列的前项和.若,求.
18.(本小题满分12分)某商场为提高服务质量,随机调查了50名男顾客和50名女顾客,每位顾客对该商场的服务给出满意或不满意的评价,得到下面列联表:
满意
不满意
男顾客
40
10
女顾客
30
20
(1)分别估计男、女顾客对该商场服务满意的概率;
(2)能否有95%的把握认为男、女顾客对该商场服务的评价有差异?
附:.
P(K2≥k)
0.050
0.010
0.001
k
3.841
6.635
10.828
19.(本小题满分12分)的内角A,B,C的对边分别为a,b,c.已知B=150°.
(1)若a=c,b=2,求的面积;
(2)若sinA+sinC=,求C.
20.(本小题满分12分)如图,在四棱锥P-ABCD中,AB//CD,且.
(1)证明:平面PAB⊥平面PAD;
(2)若PA=PD=AB=DC,,求二面角A-PB-C的余弦值.
21.(本小题满分12分已知椭圆C:
(a>b>0)的离心率为,且过点(,1).
(1)求椭圆C的方程;
(2)设直线:交C于A、B两点,0为坐标原点,求△OAB面积的最大值.
22.(本小题满分12分)
已知函数.
(1)求的单调性;
(2)设a,b为两个不相等的正数,且,证明:.
2021—2022学年度徐闻一中高三数学月考(1)
答案
一.单项选择题:
共12题,每题5分,共60分.
在每个小题给出的四个选项中,只有一项是符合题目要求的.
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
A
C
C
D
A
B
B
C
ACD
AD
BC
ACD
12.【详解】圆的圆心为,半径为,
直线的方程为,即,
圆心到直线的距离为,
所以,点到直线的距离的最小值为,最大值为,A选项正确,B选项错误;
如下图所示:
当最大或最小时,与圆相切,
连接、,可知,
,,由勾股定理可得,CD选项正确.
故选:ACD.
二.填空题:
本题共4个小题,每小题5分,共20分.
13.
14.
15.
16.1
三、解答题:(本大题共6小题,共70分)
17、解:(1)设的首项为,公差为,
由已知得,
解得.
………………3分
所以.
……………5分
(2)由(1)可得,
………………6分
是首项为4,公比为的等比数列,
……………7分
则.
………………8分
由,得,
………………9分
解得.
……………10分
【详解】(1)由题中表格可知,50名男顾客对商场服务满意的有40人,
所以男顾客对商场服务满意率估计为,
………………3分
50名女顾客对商场满意的有30人,
所以女顾客对商场服务满意率估计为,
………………6分
(2)由列联表可知,
……10分
所以能有的把握认为男、女顾客对该商场服务的评价有差异.
…………12分
19.【详解】(1)由余弦定理可得,…………3分
的面积;………………6分
(2),………………7分
………………8分
,………………10分
,………………11分
.………………12分
20.【解析】(1)由已知,得AB⊥AP,CD⊥PD.
由于AB∥CD,故AB⊥PD,
从而AB⊥平面PAD.
又AB
平面PAB,
所以平面PAB⊥平面PAD.
在平面内做,垂足为,
由(1)可知,平面,故,可得平面.…………6分
以为坐标原点,的方向为轴正方向,为单位长,建立如图所示的空间直角坐标系.…………7分
EMBED
Equation.KSEE3
22.【详解】(1)函数的定义域为,
……………1分
又,
……………3分
当时,,当时,,……………4分
故的递增区间为,递减区间为.……………5分
(2)因为,故,即,
故,
设,由(1)可知不妨设.……………6分
因为时,,时,,
故.
先证:,
若,必成立.
若,
要证:,即证,而,
故即证,即证:,其中.……………7分
设,
则,
因为,故,故,
所以,故在为增函数,所以,
故,即成立,所以成立,
综上,成立.
……………9分
设,则,
结合,可得:,
即:,故,
要证:,即证,即证,
即证:,即证:,
令,
则,
先证明一个不等式:.
……………10分
设,则,
当时,;当时,,
故在上为增函数,在上为减函数,故,
故成立
由上述不等式可得当时,,故恒成立,
故在上为减函数,故,……………11分
故成立,即成立.
综上所述,.
一?选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知集合,,则(
)
A.
B.
C.
D.
2.
已知,则(
)
A.
B.
C.
D.
3.下列函数中,与函数y=x相同的函数是(
)
某校一个课外学习小组为研究某作物种子的发芽率y和温度x(单位:°C)的关系,在20个不同的温度条件下进行种子发芽实验,由实验数据得到下面的散点图:
由此散点图,在10°C至40°C之间,下面四个回归方程类型中最适宜作为发芽率y和温度x的回归方程类型的是(
)
A.
B.
C.
D.
5.函数的零点是(
)
A.
B.
C.
D.
6.双曲线的渐近线为(
)
A.
B. C.
D.
7.已知函数,若,则(
)
A.
B.
C.
D.
8.已知,,若,则与在同一坐标系里的图象是(
)
二?选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.
9.下列表述正确的是:(
)
“”是“”的充分不必要条件
设向量,若,则
已知,满足,则
“”的否定是“”
11.下列命题为真命题的是(
)
12.已知点在圆上,点、,则(
)
A.
点到直线的距离小于
B.
点到直线的距离大于
C.
当最小时,
D.
当最大时,
三?填空题:本题共4小题,每小题5分,共20分.
13.函数的定义域为________________
14.函数,若,则_______________
15.设函数.若为奇函数,则曲线在点处的切线方程为______________________
16.函数的最小值为______.
四?解答题:本题共6小题,共70分.解答应写出文字说明?证明过程或演算步骤.
17.(本小题满分10分)已知等差数列的前项和为,,.
(1)求的通项公式;
(2)设,记为数列的前项和.若,求.
18.(本小题满分12分)某商场为提高服务质量,随机调查了50名男顾客和50名女顾客,每位顾客对该商场的服务给出满意或不满意的评价,得到下面列联表:
满意
不满意
男顾客
40
10
女顾客
30
20
(1)分别估计男、女顾客对该商场服务满意的概率;
(2)能否有95%的把握认为男、女顾客对该商场服务的评价有差异?
附:.
P(K2≥k)
0.050
0.010
0.001
k
3.841
6.635
10.828
19.(本小题满分12分)的内角A,B,C的对边分别为a,b,c.已知B=150°.
(1)若a=c,b=2,求的面积;
(2)若sinA+sinC=,求C.
20.(本小题满分12分)如图,在四棱锥P-ABCD中,AB//CD,且.
(1)证明:平面PAB⊥平面PAD;
(2)若PA=PD=AB=DC,,求二面角A-PB-C的余弦值.
21.(本小题满分12分已知椭圆C:
(a>b>0)的离心率为,且过点(,1).
(1)求椭圆C的方程;
(2)设直线:交C于A、B两点,0为坐标原点,求△OAB面积的最大值.
22.(本小题满分12分)
已知函数.
(1)求的单调性;
(2)设a,b为两个不相等的正数,且,证明:.
2021—2022学年度徐闻一中高三数学月考(1)
答案
一.单项选择题:
共12题,每题5分,共60分.
在每个小题给出的四个选项中,只有一项是符合题目要求的.
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
A
C
C
D
A
B
B
C
ACD
AD
BC
ACD
12.【详解】圆的圆心为,半径为,
直线的方程为,即,
圆心到直线的距离为,
所以,点到直线的距离的最小值为,最大值为,A选项正确,B选项错误;
如下图所示:
当最大或最小时,与圆相切,
连接、,可知,
,,由勾股定理可得,CD选项正确.
故选:ACD.
二.填空题:
本题共4个小题,每小题5分,共20分.
13.
14.
15.
16.1
三、解答题:(本大题共6小题,共70分)
17、解:(1)设的首项为,公差为,
由已知得,
解得.
………………3分
所以.
……………5分
(2)由(1)可得,
………………6分
是首项为4,公比为的等比数列,
……………7分
则.
………………8分
由,得,
………………9分
解得.
……………10分
【详解】(1)由题中表格可知,50名男顾客对商场服务满意的有40人,
所以男顾客对商场服务满意率估计为,
………………3分
50名女顾客对商场满意的有30人,
所以女顾客对商场服务满意率估计为,
………………6分
(2)由列联表可知,
……10分
所以能有的把握认为男、女顾客对该商场服务的评价有差异.
…………12分
19.【详解】(1)由余弦定理可得,…………3分
的面积;………………6分
(2),………………7分
………………8分
,………………10分
,………………11分
.………………12分
20.【解析】(1)由已知,得AB⊥AP,CD⊥PD.
由于AB∥CD,故AB⊥PD,
从而AB⊥平面PAD.
又AB
平面PAB,
所以平面PAB⊥平面PAD.
在平面内做,垂足为,
由(1)可知,平面,故,可得平面.…………6分
以为坐标原点,的方向为轴正方向,为单位长,建立如图所示的空间直角坐标系.…………7分
EMBED
Equation.KSEE3
22.【详解】(1)函数的定义域为,
……………1分
又,
……………3分
当时,,当时,,……………4分
故的递增区间为,递减区间为.……………5分
(2)因为,故,即,
故,
设,由(1)可知不妨设.……………6分
因为时,,时,,
故.
先证:,
若,必成立.
若,
要证:,即证,而,
故即证,即证:,其中.……………7分
设,
则,
因为,故,故,
所以,故在为增函数,所以,
故,即成立,所以成立,
综上,成立.
……………9分
设,则,
结合,可得:,
即:,故,
要证:,即证,即证,
即证:,即证:,
令,
则,
先证明一个不等式:.
……………10分
设,则,
当时,;当时,,
故在上为增函数,在上为减函数,故,
故成立
由上述不等式可得当时,,故恒成立,
故在上为减函数,故,……………11分
故成立,即成立.
综上所述,.
同课章节目录
