冀教版数学八年级上册17.1等腰三角形 课件(共36张PPT)
文档属性
| 名称 | 冀教版数学八年级上册17.1等腰三角形 课件(共36张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-07 00:00:00 | ||
图片预览





文档简介
(共36张PPT)
17.1
等腰三角形
图中有些你熟悉的图形吗?它们有什么共同特点?
北京五塔寺
西安半坡博物馆
体育观看台架
埃及金字塔
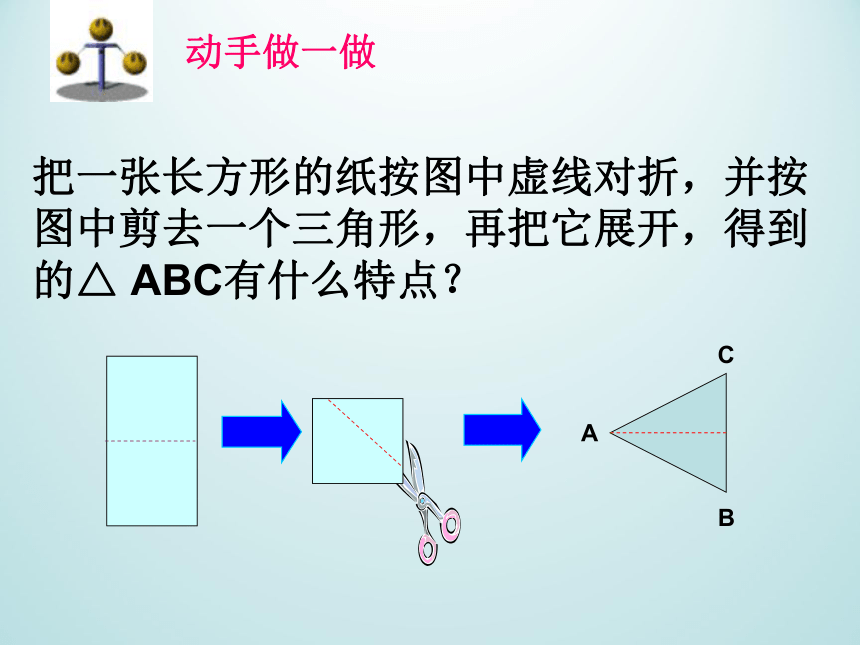
动手做一做
A
C
B
把一张长方形的纸按图中虚线对折,并按图中剪去一个三角形,再把它展开,得到的△
ABC有什么特点?
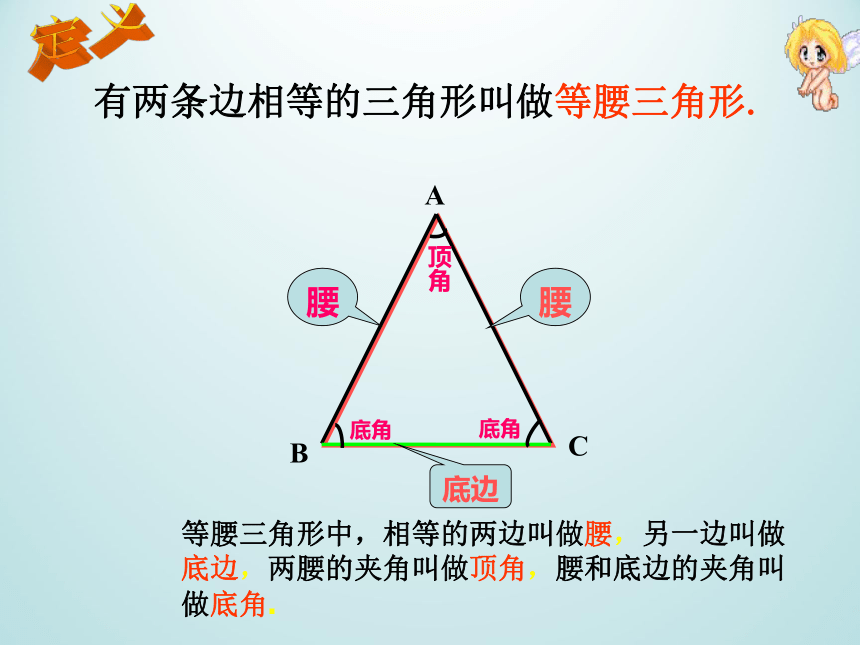
有两条边相等的三角形叫做等腰三角形.
等腰三角形中,相等的两边叫做腰,另一边叫做底边,两腰的夹角叫做顶角,腰和底边的夹角叫做底角.
A
C
B
腰
腰
底边
顶角
底角
底角
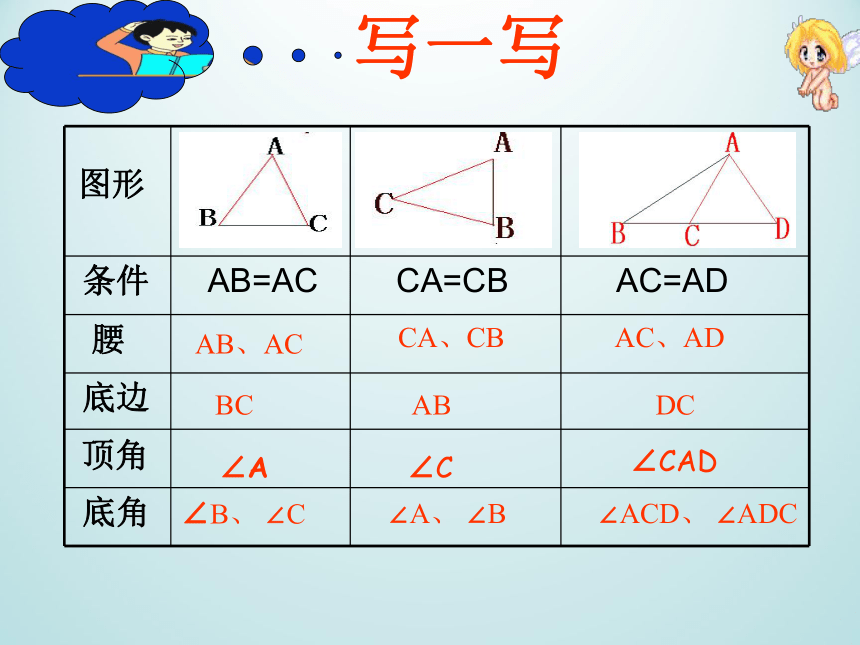
条件
AB=AC
CA=CB
AC=AD
腰
底边
底角
AB、AC
BC
∠B、
∠C
CA、CB
AB
∠A、
∠B
AC、AD
∠ACD、
∠ADC
DC
图形
顶角
∠A
∠C
∠CAD
写一写
A
C
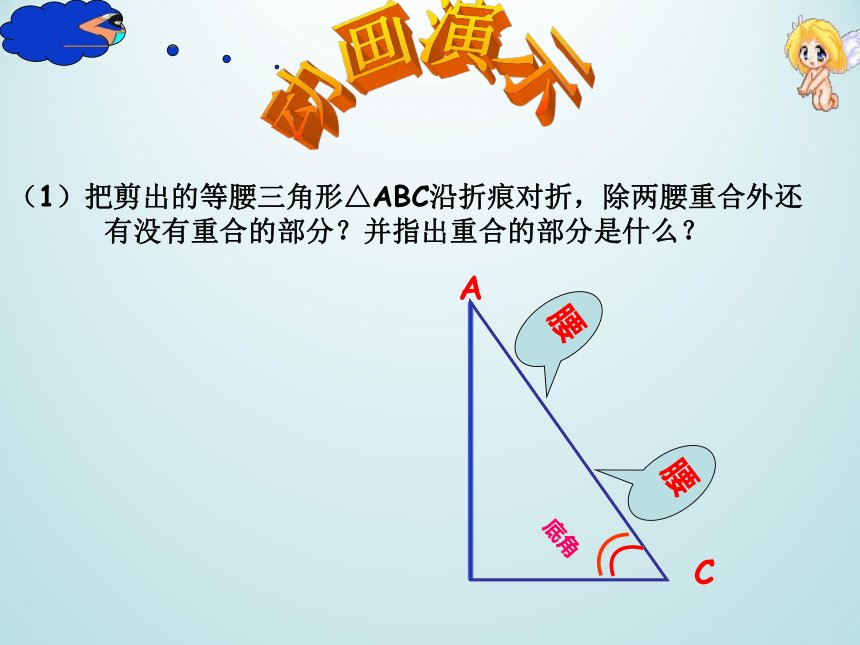
(1)把剪出的等腰三角形△ABC沿折痕对折,除两腰重合外还有没有重合的部分?并指出重合的部分是什么?
腰
腰
底角
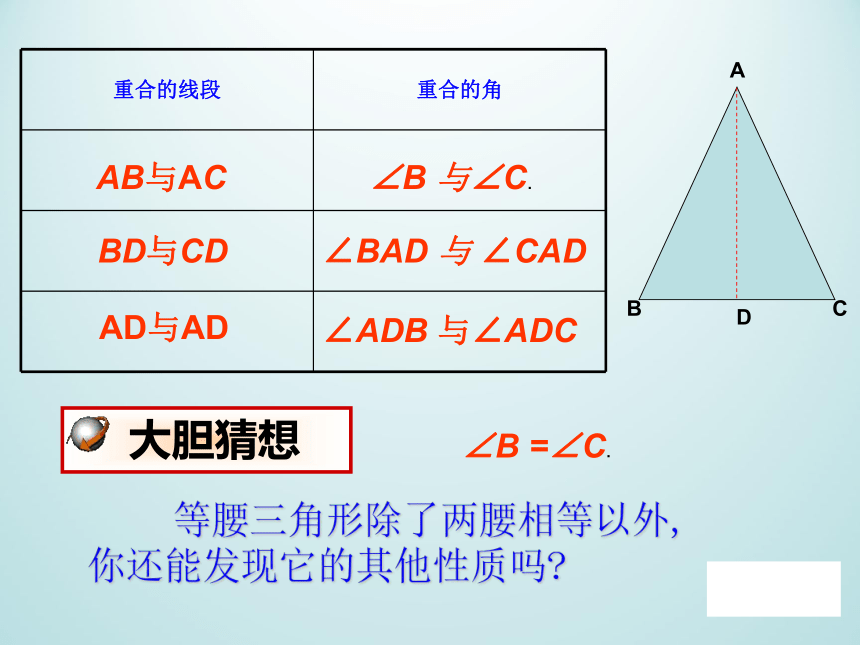
重合的线段
重合的角
A
C
B
D
AB与AC
BD与CD
AD与AD
∠B
与∠C.
∠BAD
与
∠CAD
∠ADB
与∠ADC
等腰三角形除了两腰相等以外,
你还能发现它的其他性质吗?
大胆猜想
∠B
=∠C.
猜想与论证
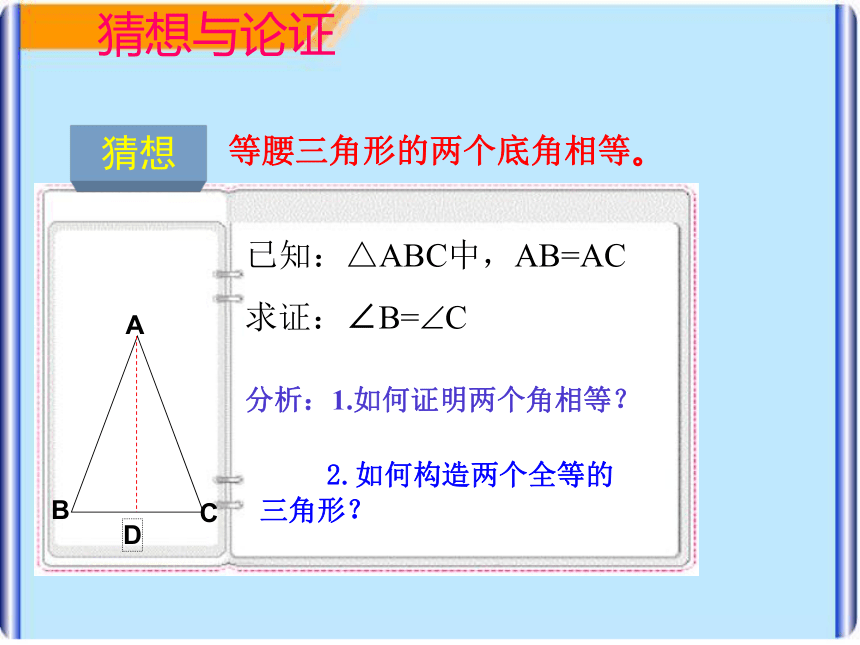
等腰三角形的两个底角相等。
已知:△ABC中,AB=AC
求证:∠B=?C
分析:1.如何证明两个角相等?
2.如何构造两个全等的三角形?
猜想
A
B
C
D
已知:
△
ABC中,AB=AC.
求证:
∠B=
∠C.
A
B
C
1
2
证明:
作顶角的平分线AD.
则∠
1=
∠
2
在△BAD和△CAD中,
AB=AC
∠
1=
∠
2
,
AD=AD
,
∴
△BAD
≌
△CAD
(SAS).
∴
∠
B=
∠C
(全等三角形的对应角相等).
证明:等腰三角形的两个底角相等
作顶角的平分线
D
证明:
作底边中线AD.则BD=CD
在△BAD和△CAD中,
AB=AC,
BD=CD
,
AD=AD,
∴
△BAD
≌
△CAD
(SSS).
∴
∠
B=
∠C
(全等三角形的对应角相等).
已知:
△
ABC中,AB=AC.
求证:
∠B=
∠C.
A
B
C
D
证明:等腰三角形的两个底角相等
作底边中线
证明:
作底边高线AD.
则∠
ADB=
∠
ADC=900
在Rt△BAD和△RtCAD中,
AB=AC
AD=AD,
∴
Rt
△BAD
≌
Rt
△CAD
(HL).
∴
∠
B=
∠C
(全等三角形的对应角相等).
已知:
△
ABC中,AB=AC.
求证:
∠B=
∠C.
A
B
C
D
证明:等腰三角形的两个底角相等
作底边的高线
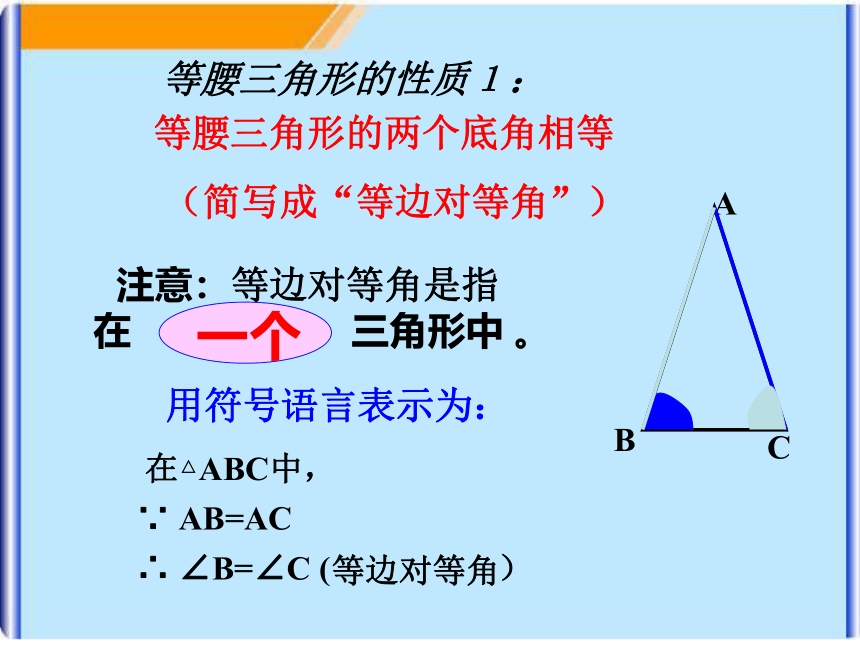
等腰三角形的性质1:
等腰三角形的两个底角相等
(简写成“等边对等角”)
注意:等边对等角是指
在
三角形中
。
一个
用符号语言表示为:
在△ABC中,
∵
AB=AC
∴
∠B=∠C
(
)
等边对等角
C
A
B
例1
(1)已知:在△ABC中,AB
=
AC,
并且其中一个角为80°,那么其它角的度数分别为_________________________.
(2)已知:在△ABC中,AB
=
AC,
并且其中一个角为100°,那么其它角的度数分别为_______________________.
50°,
50°或80°,
20°
40°,
40°
例题讲解
⒈等腰三角形一个底角为75°,它的另外两个
角为_____
__;
⒉等腰三角形一个角为70°,它的另外两个角
为___________________;
⒊等腰三角形一个角为110°,它的另外两个角
为______
__。
75°,
30°
70°,40°或55°,55°
35°,35°
小试牛刀
例2、如图,在△ABC中
,AB=AC,点D在AC上,且
BD=BC=AD,求△ABC各角的度数。
A
B
C
D
巩固提高
例3:
如图,在△ABC中,
AB=AC,BD,CE
分别为∠ABC,∠ACB
的平分线。
求证:BD=CE.
A
B
C
D
E
延
伸
与
拓
展
延
伸
与
拓
展
证明:
∵BD,CE
分别为∠ABC,∠ACB
的平分线,
∴
∠ABD=
∠ABC,
∠ACE=
∠ACB
∵
∠ABC=∠ACB
(等边对等角)
∴
∠ABD=
∠ACE(等量代换)
∵
AB=AC(已知),
∠A=
∠A(公共角)
∴
△ABD≌
△
ACE(ASA)
∴BD=CE(全等三角形对应边相等)
2
1
2
1
根据等腰三角形性质2,在△ABC中,AB=AC时
(1)
∵
AD⊥BC,∴
=
,
=
∠
∠
(2)
∵
AD是中线,
∴
,
=
⊥
∠
∠
(3)∵
AD是角平分线,
∴
,
⊥
=
BAD
CAD
BD
CD
AD
BC
BAD
CAD
AD
BC
BD
CD
A
C
B
D
例
:如图△ABC是一个屋顶的平面示意图,已知屋椽AB=AC,立柱AD⊥BC,底角∠B=40°,梁长BC=10米,则顶架上∠CAD=________度,BD=_____米.
A
B
C
D
延
伸
与
拓
展
50
5
△ABC中,AB=AC,D是BC边上的中点,
DF⊥AC于F
DE
⊥
AB
于E
.求证:DE=DF。
A
B
C
D
E
F
证明:
∵DE⊥AB,DF⊥AC(已知)
∴∠BED=∠CFD
又∵D是BC中点(已知)
∴BD=DC
∵AB=AC(已知)
∴∠B=∠C(等边对等角)
在△DBE与△DCF中
∠DEB=∠DFC(已证)
∠B=∠C(已证)
BD=DC(已证)
∴
△BDE
≌
△CDF(AAS)
∴DE=DF
方法二:连AD
。
∵AB=AC,BD=DC(已知)
∴AD是∠BAC的平分线。
(等腰三角形三线合一)
又∵DE⊥AB
DF⊥AC
∴DE=DF
(角平分线上的点到这个
角的两边距离相等)
⒈等腰三角形一个底角为75°它的另外两个角为_____
;
⒉等腰三角形一个顶角为70°它的另外两个角为_________;⒊等腰三角形一个角为80°,
它的另外两个角为
______
__
4、若等腰三角形的一个外角70°则它的底角为________
75°,
30°
50°,50°或
80°,20°
55°,55°
35°35°
1、在等腰△ABC中,AB
=10,AC
=12,则
△ABC的周长=32(
)
2、等腰三角形的两边分别是2和6,那么周长是10或14。(
)
3、等腰三角形的角平分线、中线和高互相重合。(
)
×
×
×
A
B
O
1、如图,位于在海上A、B两处的两艘救生船接到O处的遇险报警,当时测得∠A=∠B。
如果这两艘救生船以同样的速度同时出发,能不能大约同时赶到出事地点(不考虑风浪等因素)?
我是航海家
2.将一把三角尺和一个重锤如图放置,就能检查
一根横梁是否水平,你知道怎么检查吗?
D
A
B
我是建筑师
1.小红想做一个等腰三角形,于是她把一张长方形的纸沿对角线折叠,她说重合部分是一个等腰三角形,她说的对吗?为什么?
我是实践家
1
2
A
B
C’
C
E
D
3
2.如图所示,已知下列两个三角形,思考
怎样把每个三角形只剪一次,将它分成两个
等腰三角形?试一试,你一定会成功的。
120°
20
°
40
°
100
°
20
°
60
°
120°
20
°
40
°
20
°
100
°
20
°
60
°
20
°
我是小画家
课堂小结
通过本堂课的学习
我学会了…
…
我知道了…
…
我体会到…
…
小结:通过本节课的学习你有收获吗?
1、本节主要教学知识是等腰三角形的两个性质。
等腰三角形的性质
内容
应用格式
性质1
A
B
C
性质2
A
B
C
等腰三角形的
两个底角相等
等腰三角形的顶角
平分线、底边上的
中线底边上的高
互相重合。
∵AB=AC(已知)
∴∠B=∠C
(等边对等角)
①∵AB=AC,∠1=∠2(已知)
∴BD=DC,AD⊥BC(三线合一)
②
∵AB=AC,BD=DC(已知)
∴
∠1=∠2,
AD⊥BC(三线合一)
③∵
AB=AC,
AD⊥BC
(已知)
∴
∠1=∠2,
BD=DC(三线合一)
D
1
2
2、本节课学习了数学思想及方法:分类讨论和一题多解。
1、课本P143
A组
1、3、4,B组1、2。
2、用两种方法证明等腰三角形底角相等.
(用符号语言说明)
一次数学课上,老师布置了一道几何证明题,通过大家的激烈讨论得到了许多种证明方法,聪明的你们,能找出几种证明方法呢?试试看吧!
如图,已知△ABC中,AB=AC,F在AC上,在BA的延长线上截取AE=AF,求证:ED⊥BC
A
B
C
D
E
F
课后思考
已知:如图,
△
ABC中,
∠ABC=50
?,
∠ACB=80
?,延长CB至D,使BD=BA,延长BC至E,使CE=CA
.连结AD、AE.
求∠D、∠E、∠DAE的度数
.
A
B
C
D
E
∵BD=CD
∴∠D=∠DAB
∵
∠ABC=∠D+∠DAB
∴∠D=
∠ABC=250
1
2
__
∵CE=CA
∴∠E=∠CAE
∵
∠ACB=∠E+∠CAE
∴∠E=
∠ACB=400
1
2
__
∵
∠DAE+∠E+∠D=1800
∴∠DAE=
1800-250-400=1150
解:
下课了!
17.1
等腰三角形
图中有些你熟悉的图形吗?它们有什么共同特点?
北京五塔寺
西安半坡博物馆
体育观看台架
埃及金字塔
动手做一做
A
C
B
把一张长方形的纸按图中虚线对折,并按图中剪去一个三角形,再把它展开,得到的△
ABC有什么特点?
有两条边相等的三角形叫做等腰三角形.
等腰三角形中,相等的两边叫做腰,另一边叫做底边,两腰的夹角叫做顶角,腰和底边的夹角叫做底角.
A
C
B
腰
腰
底边
顶角
底角
底角
条件
AB=AC
CA=CB
AC=AD
腰
底边
底角
AB、AC
BC
∠B、
∠C
CA、CB
AB
∠A、
∠B
AC、AD
∠ACD、
∠ADC
DC
图形
顶角
∠A
∠C
∠CAD
写一写
A
C
(1)把剪出的等腰三角形△ABC沿折痕对折,除两腰重合外还有没有重合的部分?并指出重合的部分是什么?
腰
腰
底角
重合的线段
重合的角
A
C
B
D
AB与AC
BD与CD
AD与AD
∠B
与∠C.
∠BAD
与
∠CAD
∠ADB
与∠ADC
等腰三角形除了两腰相等以外,
你还能发现它的其他性质吗?
大胆猜想
∠B
=∠C.
猜想与论证
等腰三角形的两个底角相等。
已知:△ABC中,AB=AC
求证:∠B=?C
分析:1.如何证明两个角相等?
2.如何构造两个全等的三角形?
猜想
A
B
C
D
已知:
△
ABC中,AB=AC.
求证:
∠B=
∠C.
A
B
C
1
2
证明:
作顶角的平分线AD.
则∠
1=
∠
2
在△BAD和△CAD中,
AB=AC
∠
1=
∠
2
,
AD=AD
,
∴
△BAD
≌
△CAD
(SAS).
∴
∠
B=
∠C
(全等三角形的对应角相等).
证明:等腰三角形的两个底角相等
作顶角的平分线
D
证明:
作底边中线AD.则BD=CD
在△BAD和△CAD中,
AB=AC,
BD=CD
,
AD=AD,
∴
△BAD
≌
△CAD
(SSS).
∴
∠
B=
∠C
(全等三角形的对应角相等).
已知:
△
ABC中,AB=AC.
求证:
∠B=
∠C.
A
B
C
D
证明:等腰三角形的两个底角相等
作底边中线
证明:
作底边高线AD.
则∠
ADB=
∠
ADC=900
在Rt△BAD和△RtCAD中,
AB=AC
AD=AD,
∴
Rt
△BAD
≌
Rt
△CAD
(HL).
∴
∠
B=
∠C
(全等三角形的对应角相等).
已知:
△
ABC中,AB=AC.
求证:
∠B=
∠C.
A
B
C
D
证明:等腰三角形的两个底角相等
作底边的高线
等腰三角形的性质1:
等腰三角形的两个底角相等
(简写成“等边对等角”)
注意:等边对等角是指
在
三角形中
。
一个
用符号语言表示为:
在△ABC中,
∵
AB=AC
∴
∠B=∠C
(
)
等边对等角
C
A
B
例1
(1)已知:在△ABC中,AB
=
AC,
并且其中一个角为80°,那么其它角的度数分别为_________________________.
(2)已知:在△ABC中,AB
=
AC,
并且其中一个角为100°,那么其它角的度数分别为_______________________.
50°,
50°或80°,
20°
40°,
40°
例题讲解
⒈等腰三角形一个底角为75°,它的另外两个
角为_____
__;
⒉等腰三角形一个角为70°,它的另外两个角
为___________________;
⒊等腰三角形一个角为110°,它的另外两个角
为______
__。
75°,
30°
70°,40°或55°,55°
35°,35°
小试牛刀
例2、如图,在△ABC中
,AB=AC,点D在AC上,且
BD=BC=AD,求△ABC各角的度数。
A
B
C
D
巩固提高
例3:
如图,在△ABC中,
AB=AC,BD,CE
分别为∠ABC,∠ACB
的平分线。
求证:BD=CE.
A
B
C
D
E
延
伸
与
拓
展
延
伸
与
拓
展
证明:
∵BD,CE
分别为∠ABC,∠ACB
的平分线,
∴
∠ABD=
∠ABC,
∠ACE=
∠ACB
∵
∠ABC=∠ACB
(等边对等角)
∴
∠ABD=
∠ACE(等量代换)
∵
AB=AC(已知),
∠A=
∠A(公共角)
∴
△ABD≌
△
ACE(ASA)
∴BD=CE(全等三角形对应边相等)
2
1
2
1
根据等腰三角形性质2,在△ABC中,AB=AC时
(1)
∵
AD⊥BC,∴
=
,
=
∠
∠
(2)
∵
AD是中线,
∴
,
=
⊥
∠
∠
(3)∵
AD是角平分线,
∴
,
⊥
=
BAD
CAD
BD
CD
AD
BC
BAD
CAD
AD
BC
BD
CD
A
C
B
D
例
:如图△ABC是一个屋顶的平面示意图,已知屋椽AB=AC,立柱AD⊥BC,底角∠B=40°,梁长BC=10米,则顶架上∠CAD=________度,BD=_____米.
A
B
C
D
延
伸
与
拓
展
50
5
△ABC中,AB=AC,D是BC边上的中点,
DF⊥AC于F
DE
⊥
AB
于E
.求证:DE=DF。
A
B
C
D
E
F
证明:
∵DE⊥AB,DF⊥AC(已知)
∴∠BED=∠CFD
又∵D是BC中点(已知)
∴BD=DC
∵AB=AC(已知)
∴∠B=∠C(等边对等角)
在△DBE与△DCF中
∠DEB=∠DFC(已证)
∠B=∠C(已证)
BD=DC(已证)
∴
△BDE
≌
△CDF(AAS)
∴DE=DF
方法二:连AD
。
∵AB=AC,BD=DC(已知)
∴AD是∠BAC的平分线。
(等腰三角形三线合一)
又∵DE⊥AB
DF⊥AC
∴DE=DF
(角平分线上的点到这个
角的两边距离相等)
⒈等腰三角形一个底角为75°它的另外两个角为_____
;
⒉等腰三角形一个顶角为70°它的另外两个角为_________;⒊等腰三角形一个角为80°,
它的另外两个角为
______
__
4、若等腰三角形的一个外角70°则它的底角为________
75°,
30°
50°,50°或
80°,20°
55°,55°
35°35°
1、在等腰△ABC中,AB
=10,AC
=12,则
△ABC的周长=32(
)
2、等腰三角形的两边分别是2和6,那么周长是10或14。(
)
3、等腰三角形的角平分线、中线和高互相重合。(
)
×
×
×
A
B
O
1、如图,位于在海上A、B两处的两艘救生船接到O处的遇险报警,当时测得∠A=∠B。
如果这两艘救生船以同样的速度同时出发,能不能大约同时赶到出事地点(不考虑风浪等因素)?
我是航海家
2.将一把三角尺和一个重锤如图放置,就能检查
一根横梁是否水平,你知道怎么检查吗?
D
A
B
我是建筑师
1.小红想做一个等腰三角形,于是她把一张长方形的纸沿对角线折叠,她说重合部分是一个等腰三角形,她说的对吗?为什么?
我是实践家
1
2
A
B
C’
C
E
D
3
2.如图所示,已知下列两个三角形,思考
怎样把每个三角形只剪一次,将它分成两个
等腰三角形?试一试,你一定会成功的。
120°
20
°
40
°
100
°
20
°
60
°
120°
20
°
40
°
20
°
100
°
20
°
60
°
20
°
我是小画家
课堂小结
通过本堂课的学习
我学会了…
…
我知道了…
…
我体会到…
…
小结:通过本节课的学习你有收获吗?
1、本节主要教学知识是等腰三角形的两个性质。
等腰三角形的性质
内容
应用格式
性质1
A
B
C
性质2
A
B
C
等腰三角形的
两个底角相等
等腰三角形的顶角
平分线、底边上的
中线底边上的高
互相重合。
∵AB=AC(已知)
∴∠B=∠C
(等边对等角)
①∵AB=AC,∠1=∠2(已知)
∴BD=DC,AD⊥BC(三线合一)
②
∵AB=AC,BD=DC(已知)
∴
∠1=∠2,
AD⊥BC(三线合一)
③∵
AB=AC,
AD⊥BC
(已知)
∴
∠1=∠2,
BD=DC(三线合一)
D
1
2
2、本节课学习了数学思想及方法:分类讨论和一题多解。
1、课本P143
A组
1、3、4,B组1、2。
2、用两种方法证明等腰三角形底角相等.
(用符号语言说明)
一次数学课上,老师布置了一道几何证明题,通过大家的激烈讨论得到了许多种证明方法,聪明的你们,能找出几种证明方法呢?试试看吧!
如图,已知△ABC中,AB=AC,F在AC上,在BA的延长线上截取AE=AF,求证:ED⊥BC
A
B
C
D
E
F
课后思考
已知:如图,
△
ABC中,
∠ABC=50
?,
∠ACB=80
?,延长CB至D,使BD=BA,延长BC至E,使CE=CA
.连结AD、AE.
求∠D、∠E、∠DAE的度数
.
A
B
C
D
E
∵BD=CD
∴∠D=∠DAB
∵
∠ABC=∠D+∠DAB
∴∠D=
∠ABC=250
1
2
__
∵CE=CA
∴∠E=∠CAE
∵
∠ACB=∠E+∠CAE
∴∠E=
∠ACB=400
1
2
__
∵
∠DAE+∠E+∠D=1800
∴∠DAE=
1800-250-400=1150
解:
下课了!
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
