冀教版数学八年级上册 17.1等腰三角形 课件 (共28张PPT)
文档属性
| 名称 | 冀教版数学八年级上册 17.1等腰三角形 课件 (共28张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 4.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-07 14:05:54 | ||
图片预览







文档简介
(共28张PPT)
17.1等腰三角形
魁星阁
一、创设情景,激发兴趣
天安门
欧式别墅
从数学的观点去思考,你观察到了什么图形?
埃菲尔铁塔
1.
巩固等腰三角形概念,掌握等腰三角形的性质。
灵活应用等腰三角形的性质解决实际问题。
体会探索数学结论的过程,发展推理能力。
学习目标
2.
3.
基本概念
随堂练习
性质探索
学以致用
定理总结
教学过程
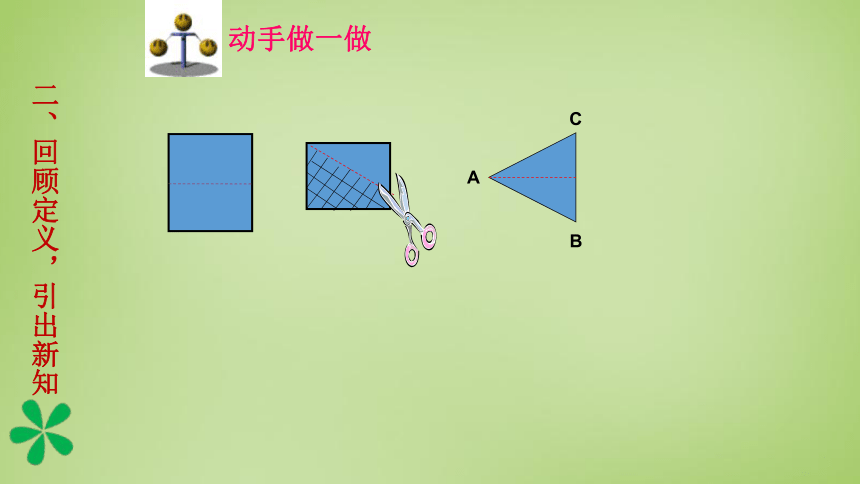
动手做一做
A
C
B
二、回顾定义,引出新知
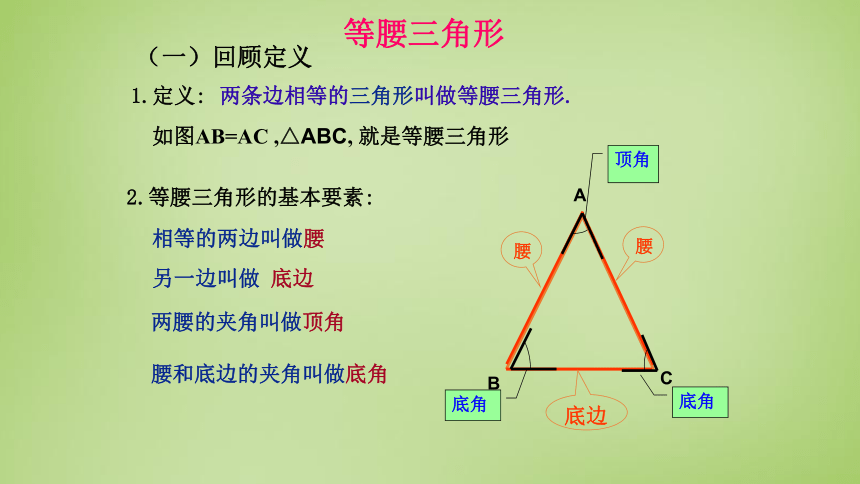
等腰三角形
(一)回顾定义
1.定义:
两条边相等的三角形叫做等腰三角形.
如图AB=AC
,△ABC,
就是等腰三角形
2.等腰三角形的基本要素:
相等的两边叫做腰
另一边叫做
底边
两腰的夹角叫做顶角
腰和底边的夹角叫做底角
A
B
C
腰
腰
底边
顶角
底角
底角
C
A
B
AC=BC
B
C
A
AB=CB
腰:
底边:
顶角:
底角:
腰:
底边:
顶角:
底角:
AC,BC
AB
A,
B
AB,CB
AC
B
A,
C
C
做一做1:
(1)剪出的三角形是轴对称图形吗?你能发现这个三角形有哪些特点吗?说一说你的猜想。
(2)把三角形的顶角顶点记为A,底角顶点记为B,C。
(3)把三角形对折,让两腰AB,AC重叠在一起,折痕为AD。
观察后你发现了什么现象?
(二)引出新知
B
A
C
D
A
B
C
D
等腰三角形是轴对称图形,顶角平分线所在的直线是它的对称轴。
重合的线段
重合的角
A
B
D
AB=AC
BD=CD
AD=AD
∠B
=
∠C
∠BAD
=
∠CAD
∠ADB
=
∠ADC=
90°
C
∟
1.
等腰三角形是轴对称图形
2.
∠
B
=∠
C
3.
BD
=
CD
,AD
为底边上的中线
4.
∠ADB
=
∠ADC
=
90°,AD为底边上的高
5.
∠BAD
=
∠CAD
,AD为顶角平分线
问题1.
结论
2
用文字如何表述?
等腰三角形的两个底角相等
(简写“等边对等角”)
C
A
B
D
∟
(2)要注意是哪三线?
等腰三角形的顶角平分线、底边上的中线
和底边上的高互相重合,简称“三线合一”。
(1)“等腰三角形”是三线合一的大前提
C
A
B
D
问题2.
结论
3
、
4
、
5
用一句话可以归纳为什么?
∟
做一做2:画出手中等腰三角形的某一底角平分线、对
边(腰)上的中线和高,看是否重合?
C
B
A
如图:BF为AC边上的高,BE为
ABC的
平分线,BG为AC边上的中线
E
F
G
没有重合
C
A
B
D
如何证明:等腰三角形的两个底角相等(简写“等边对等角”)
已知:如图△ABC中AB=AC
求证:∠B=∠C
证明:过A作AD⊥BC于D
∟
在Rt△ABD和Rt△ACD中
AB=AC(已知)
AD=AD(公共边)
∴
Rt△ABD≌Rt△ACD(HL)
∴∠B=∠C(全等三角形的对应角相等)
思考1:还有其他的证明方法吗?
思考2:你有办法证明等腰三角形的“三线合一”吗?
三、实践探索,感受性质
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
┓
顶角平分线
底边上的高
底边上的中线
A
B
C
D
A
B
C
D
┓
A
B
C
D
A
B
C
D
三
线
合
一
(三)等腰三角形的性质
1.
等腰三角形的两个底角相等
(简称“等边对等角”)
2.
等腰三角形的
顶角平分线、底边上的高和底边上的中线
互相重合(简称“三线合一”)
文字表述
C
D
B
A
①在ΔABC中,∵AB=AC,
∴
∠B=∠C(
)
(三)等腰三角形的性质
等边对等角
(1)∵AD⊥BC,
∴∠____
=
∠____,___=
___
(2)∵AD是中线,∴___⊥___
,∠____
=∠____
(3)∵AD是角平分线,
∴___
⊥___
,___
=___
BAD
CAD
BD
CD
AD
BC
AD
BC
BAD
CAD
BD
CD
②在△ABC中,
AB=AC时,
等腰三角形底边上的中线和高线、顶角的平分线互相重合。
几何语言
例1、已知:在△ABC中,AB
=
AC,∠B
=
80°,
求∠C
和
∠A的度数。
A
B
C
解:
∵
AB
=AC
∴
∠B
=
∠C
=
80°
又
∵
∠A
+
∠
B
+
∠C
=
180°
∴
∠A
=
180°-
80°
-
80°=
20°
四、合作交流,拓展提高
例2、如图,在△ABC中,AB
=
AC,D是BC边上的中点,
∠B
=
30°,求
∠BAD
和
∠ADC的度数。
A
B
C
D
解:
∵等腰三角形的“三线合一”
所以AD是△ABC的顶角平分线、
底边上的高,
∠ADC
=
∠ADB=
90°
∵
∠
BAD
=180°
-
∠ADB
-
∠B
=
60°
∴
∠
BAD
=
60°
∴
例3、如图,在△ABC中
,AB=AC,点D在AC上,且
BD=BC=AD,求△ABC各角的度数。
A
B
C
D
解:∵AB=AC,BD=BC=AD,
∴∠ABC=∠C=∠BDC,∠A=∠ABD
(等边对等角)
设∠A=x,则∠BDC=
∠A+
∠ABD=2x,
从而∠ABC=
∠C=
∠BDC=2x,
∴∠A+∠ABC+∠C=x+2x+2x=180°,
解得x=36°,
∴∠A=36°∠ABC=∠C=72°
x
⌒
2x
2x
⌒
⌒
2x
⌒
人们把顶角为36°,两个底角为72°的等腰三角形叫做黄金三角形,因为它的底与一腰之长之比为黄金比(大约为0.618),这种等腰三角形既标准又美观,被众多著名建筑家喜爱。
学以致用
将一把三角尺和一个重锤如图放置,就能检查
一根横梁是否水平,你知道为什么吗?
你能解决前面提出的问题吗?
能。当重锤经过等腰直角三角尺斜边的中点时,重锤线与斜边上的高线叠合,即斜边与重锤线垂直,所以斜边与横梁是水平的。
A
B
C
D
1
2
“三线合一”.
1.等腰三角形一个角为70°,它的另外两个角为
___________________
2.等腰三角形一个角为110°,它的另外两个角为
________
70°,40°或55°,55°(分类讨论)
35°,35°
3.等腰三角形有两边长为4和8,则该等腰三角形的周长为______。
练习一、填空
20
五、巩固练习,强化新知
练习二、
在△ABC中,AC=BC,∠ACB=90°,CD⊥AB
则图中有哪些角和线段相等?
A
C
B
D
∵
AC=BC,
∠ACB=90°
∠ADC=∠BDC=∠ACB=90°
解:
∠A=
∠B=45
°
∴
∵
CD⊥AB
∴
∠ACD=
∠A=
∠B=
∠BCD
=45
°
∠ACD=
180
°
-
∠ADC-
∠A
=45°
∠BCD=180°-
∠BDC-
∠B=45
°
∴
∴
AD=BD=DC
(“等边对等角”)
∴
相等的线段有:AC=BC,
AD=BD=DC
相等的角有:ADC=∠BDC=∠ACB=90°
∠BCD=
∠ACD=
∠A=
∠B=45°
谢谢大家
THANKS!
17.1等腰三角形
魁星阁
一、创设情景,激发兴趣
天安门
欧式别墅
从数学的观点去思考,你观察到了什么图形?
埃菲尔铁塔
1.
巩固等腰三角形概念,掌握等腰三角形的性质。
灵活应用等腰三角形的性质解决实际问题。
体会探索数学结论的过程,发展推理能力。
学习目标
2.
3.
基本概念
随堂练习
性质探索
学以致用
定理总结
教学过程
动手做一做
A
C
B
二、回顾定义,引出新知
等腰三角形
(一)回顾定义
1.定义:
两条边相等的三角形叫做等腰三角形.
如图AB=AC
,△ABC,
就是等腰三角形
2.等腰三角形的基本要素:
相等的两边叫做腰
另一边叫做
底边
两腰的夹角叫做顶角
腰和底边的夹角叫做底角
A
B
C
腰
腰
底边
顶角
底角
底角
C
A
B
AC=BC
B
C
A
AB=CB
腰:
底边:
顶角:
底角:
腰:
底边:
顶角:
底角:
AC,BC
AB
A,
B
AB,CB
AC
B
A,
C
C
做一做1:
(1)剪出的三角形是轴对称图形吗?你能发现这个三角形有哪些特点吗?说一说你的猜想。
(2)把三角形的顶角顶点记为A,底角顶点记为B,C。
(3)把三角形对折,让两腰AB,AC重叠在一起,折痕为AD。
观察后你发现了什么现象?
(二)引出新知
B
A
C
D
A
B
C
D
等腰三角形是轴对称图形,顶角平分线所在的直线是它的对称轴。
重合的线段
重合的角
A
B
D
AB=AC
BD=CD
AD=AD
∠B
=
∠C
∠BAD
=
∠CAD
∠ADB
=
∠ADC=
90°
C
∟
1.
等腰三角形是轴对称图形
2.
∠
B
=∠
C
3.
BD
=
CD
,AD
为底边上的中线
4.
∠ADB
=
∠ADC
=
90°,AD为底边上的高
5.
∠BAD
=
∠CAD
,AD为顶角平分线
问题1.
结论
2
用文字如何表述?
等腰三角形的两个底角相等
(简写“等边对等角”)
C
A
B
D
∟
(2)要注意是哪三线?
等腰三角形的顶角平分线、底边上的中线
和底边上的高互相重合,简称“三线合一”。
(1)“等腰三角形”是三线合一的大前提
C
A
B
D
问题2.
结论
3
、
4
、
5
用一句话可以归纳为什么?
∟
做一做2:画出手中等腰三角形的某一底角平分线、对
边(腰)上的中线和高,看是否重合?
C
B
A
如图:BF为AC边上的高,BE为
ABC的
平分线,BG为AC边上的中线
E
F
G
没有重合
C
A
B
D
如何证明:等腰三角形的两个底角相等(简写“等边对等角”)
已知:如图△ABC中AB=AC
求证:∠B=∠C
证明:过A作AD⊥BC于D
∟
在Rt△ABD和Rt△ACD中
AB=AC(已知)
AD=AD(公共边)
∴
Rt△ABD≌Rt△ACD(HL)
∴∠B=∠C(全等三角形的对应角相等)
思考1:还有其他的证明方法吗?
思考2:你有办法证明等腰三角形的“三线合一”吗?
三、实践探索,感受性质
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
┓
顶角平分线
底边上的高
底边上的中线
A
B
C
D
A
B
C
D
┓
A
B
C
D
A
B
C
D
三
线
合
一
(三)等腰三角形的性质
1.
等腰三角形的两个底角相等
(简称“等边对等角”)
2.
等腰三角形的
顶角平分线、底边上的高和底边上的中线
互相重合(简称“三线合一”)
文字表述
C
D
B
A
①在ΔABC中,∵AB=AC,
∴
∠B=∠C(
)
(三)等腰三角形的性质
等边对等角
(1)∵AD⊥BC,
∴∠____
=
∠____,___=
___
(2)∵AD是中线,∴___⊥___
,∠____
=∠____
(3)∵AD是角平分线,
∴___
⊥___
,___
=___
BAD
CAD
BD
CD
AD
BC
AD
BC
BAD
CAD
BD
CD
②在△ABC中,
AB=AC时,
等腰三角形底边上的中线和高线、顶角的平分线互相重合。
几何语言
例1、已知:在△ABC中,AB
=
AC,∠B
=
80°,
求∠C
和
∠A的度数。
A
B
C
解:
∵
AB
=AC
∴
∠B
=
∠C
=
80°
又
∵
∠A
+
∠
B
+
∠C
=
180°
∴
∠A
=
180°-
80°
-
80°=
20°
四、合作交流,拓展提高
例2、如图,在△ABC中,AB
=
AC,D是BC边上的中点,
∠B
=
30°,求
∠BAD
和
∠ADC的度数。
A
B
C
D
解:
∵等腰三角形的“三线合一”
所以AD是△ABC的顶角平分线、
底边上的高,
∠ADC
=
∠ADB=
90°
∵
∠
BAD
=180°
-
∠ADB
-
∠B
=
60°
∴
∠
BAD
=
60°
∴
例3、如图,在△ABC中
,AB=AC,点D在AC上,且
BD=BC=AD,求△ABC各角的度数。
A
B
C
D
解:∵AB=AC,BD=BC=AD,
∴∠ABC=∠C=∠BDC,∠A=∠ABD
(等边对等角)
设∠A=x,则∠BDC=
∠A+
∠ABD=2x,
从而∠ABC=
∠C=
∠BDC=2x,
∴∠A+∠ABC+∠C=x+2x+2x=180°,
解得x=36°,
∴∠A=36°∠ABC=∠C=72°
x
⌒
2x
2x
⌒
⌒
2x
⌒
人们把顶角为36°,两个底角为72°的等腰三角形叫做黄金三角形,因为它的底与一腰之长之比为黄金比(大约为0.618),这种等腰三角形既标准又美观,被众多著名建筑家喜爱。
学以致用
将一把三角尺和一个重锤如图放置,就能检查
一根横梁是否水平,你知道为什么吗?
你能解决前面提出的问题吗?
能。当重锤经过等腰直角三角尺斜边的中点时,重锤线与斜边上的高线叠合,即斜边与重锤线垂直,所以斜边与横梁是水平的。
A
B
C
D
1
2
“三线合一”.
1.等腰三角形一个角为70°,它的另外两个角为
___________________
2.等腰三角形一个角为110°,它的另外两个角为
________
70°,40°或55°,55°(分类讨论)
35°,35°
3.等腰三角形有两边长为4和8,则该等腰三角形的周长为______。
练习一、填空
20
五、巩固练习,强化新知
练习二、
在△ABC中,AC=BC,∠ACB=90°,CD⊥AB
则图中有哪些角和线段相等?
A
C
B
D
∵
AC=BC,
∠ACB=90°
∠ADC=∠BDC=∠ACB=90°
解:
∠A=
∠B=45
°
∴
∵
CD⊥AB
∴
∠ACD=
∠A=
∠B=
∠BCD
=45
°
∠ACD=
180
°
-
∠ADC-
∠A
=45°
∠BCD=180°-
∠BDC-
∠B=45
°
∴
∴
AD=BD=DC
(“等边对等角”)
∴
相等的线段有:AC=BC,
AD=BD=DC
相等的角有:ADC=∠BDC=∠ACB=90°
∠BCD=
∠ACD=
∠A=
∠B=45°
谢谢大家
THANKS!
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
