冀教版数学八年级上册17.2直角三角形 课件(共17张PPT)
文档属性
| 名称 | 冀教版数学八年级上册17.2直角三角形 课件(共17张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 560.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-07 14:10:47 | ||
图片预览





文档简介
(共17张PPT)
17.2直角三角形
学习目标
1.掌握直角三角形的性质定理和判定定理
2.掌握含30?角的直角三角形的性质
学习重点和难点
重点:
直角三角形的性质定理和判定定理
难点:
含30?角的直角三角形的性质
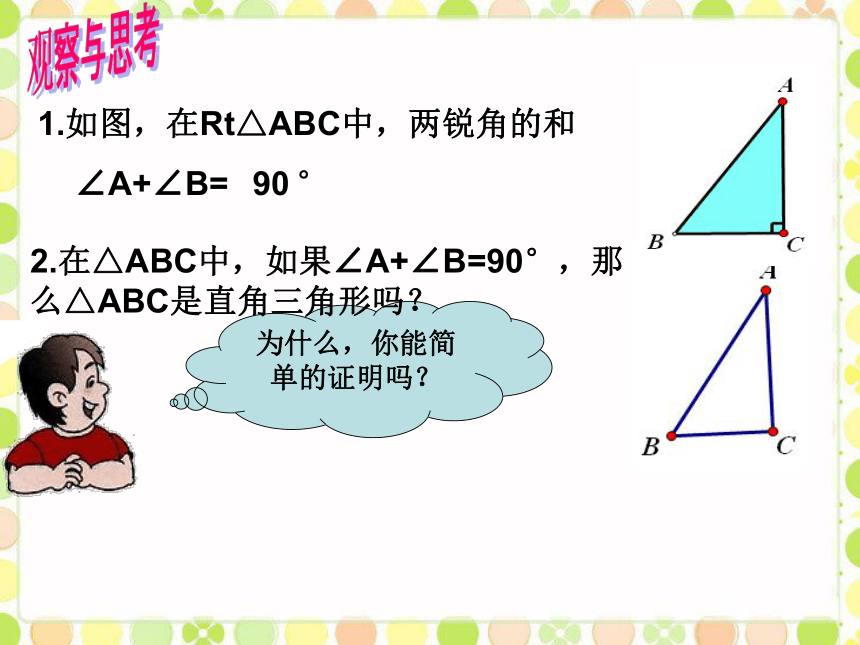
1.如图,在Rt△ABC中,两锐角的和
∠A+∠B=
为什么,你能简单的证明吗?
90
°
2.在△ABC中,如果∠A+∠B=90°,那么△ABC是直角三角形吗?
直角三角形的性质定理:
直角三角形的两个锐角互余.
直角三角形的判定定理:
如果一个三角形的两个角互余,那么这个三角形是直角三角形.
147页
观察与思考
直角三角形的性质定理
直角三角形斜边上的中线等于斜边的一半.
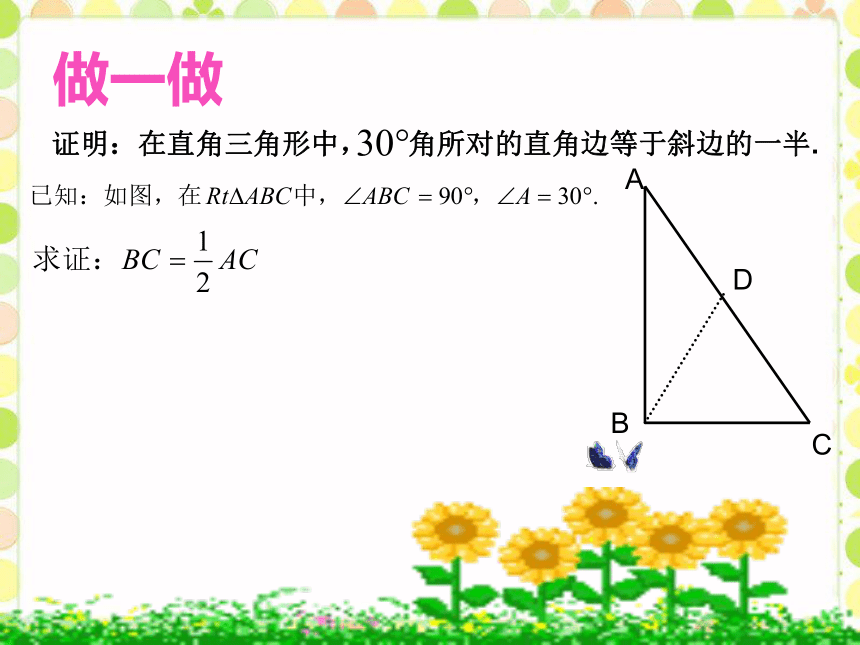
做一做
证明:在直角三角形中,
角所对的直角边等于斜边的一半.
A
B
C
D
分析:如果中线CD=
AB,则有∠ACD=
∠A.
于是受到启发,在图中,过Rt
△ABC的直角
顶点C作射线CD'交AB于D',使∠1=∠A,
则有A
D'
=C
D'
(
等角对等边)
直角三角形的两锐角互余
又∵∠A+∠B=90°(
)
∠1+∠2=90°
∴
∠2=
∠B
于是得
B
D'
=C
D'
(
)
等角对等边
故得
B
D'
=A
D'
=C
D'
=
AB
所以D是斜边AB上的中点,即C
D'是斜边AB上的中线,从而C
D'与CD重合,并有CD=
AB
直角三角形的性质定理:
在直角三角形中,斜边上的中线等于斜边的一半
1.阅读课本148页的“发现”的证明过程.
2.通过阅读你有什么发现?
∵CD是直角三角形ABC斜边上的中线
∴CD=
AB
如图,在Rt△ABC中,∠BCA=90°,如果∠A=30°,那么BC与斜边AB有什么关系?
C
B
A
D
取线段AB的中点D,连结CD,即CD为Rt△ABC斜边AB上的中线,则有CD=
AB=BD
由此可得出结论:
在直角三角形中,如果有一个锐角等于30°,那么它所对的直角边等于斜边的一半
你能用等边三角形的性质来证明直角三角形的
这条性质吗?
想一想
如图,在Rt△ABC中,如果BC=
AB,那么∠A等于多少度?
由此可得出结论:
在直角三角形中,如果一条直角边等于斜边的一半,那么这条直角边所对的角等于30°
例2
在A岛周围20海里(1海里=1852
m)水域内有暗礁,一轮船由西向东航行到O处时,发现A到在北偏东60°的方向,且与轮船相距
海里,如图所示.该船如果保持航向不变,有触礁的危险吗?
北
60°
如果三角形一边上的中线等于这条边的一半,求证:这个三角形是直角三角形
已知:CD是
△ABC的
AB边上的中线,且CD=
AB
求证:
△ABC是直角三角形
2.
如图,AC=AD,∠C,∠D是直角,将上述条件标注在图中,你能说明BC与BD相等吗?
C
D
A
B
解:在Rt△ACB和Rt△ADB中,则
AB=AB,
AC=AD.
∴
Rt△ACB≌Rt△ADB
(HL).
∴BC=BD
(全等三角形对应边相等).
2.
如图,两根长度为12米的绳子,一端系在旗杆上,另一端分别固定在地面两个木桩上,两个木桩离旗杆底部的距离相等吗?请说明你的理由.
所以Rt△ABD≌Rt△ACD(
HL
)
所以BD=CD
解:BD=CD
因为∠ADB=∠ADC=90°
在Rt△ABD和Rt△ACD中
AB=AC
AD=AD
在Rt△ABC中,
∠A
:∠B:
∠C
=1:2:3
,若AB=10cm,求BC的长
2.教材149页A组、B组
小结:这节课你有什么收获呢?与你的同伴进行交流
17.2直角三角形
学习目标
1.掌握直角三角形的性质定理和判定定理
2.掌握含30?角的直角三角形的性质
学习重点和难点
重点:
直角三角形的性质定理和判定定理
难点:
含30?角的直角三角形的性质
1.如图,在Rt△ABC中,两锐角的和
∠A+∠B=
为什么,你能简单的证明吗?
90
°
2.在△ABC中,如果∠A+∠B=90°,那么△ABC是直角三角形吗?
直角三角形的性质定理:
直角三角形的两个锐角互余.
直角三角形的判定定理:
如果一个三角形的两个角互余,那么这个三角形是直角三角形.
147页
观察与思考
直角三角形的性质定理
直角三角形斜边上的中线等于斜边的一半.
做一做
证明:在直角三角形中,
角所对的直角边等于斜边的一半.
A
B
C
D
分析:如果中线CD=
AB,则有∠ACD=
∠A.
于是受到启发,在图中,过Rt
△ABC的直角
顶点C作射线CD'交AB于D',使∠1=∠A,
则有A
D'
=C
D'
(
等角对等边)
直角三角形的两锐角互余
又∵∠A+∠B=90°(
)
∠1+∠2=90°
∴
∠2=
∠B
于是得
B
D'
=C
D'
(
)
等角对等边
故得
B
D'
=A
D'
=C
D'
=
AB
所以D是斜边AB上的中点,即C
D'是斜边AB上的中线,从而C
D'与CD重合,并有CD=
AB
直角三角形的性质定理:
在直角三角形中,斜边上的中线等于斜边的一半
1.阅读课本148页的“发现”的证明过程.
2.通过阅读你有什么发现?
∵CD是直角三角形ABC斜边上的中线
∴CD=
AB
如图,在Rt△ABC中,∠BCA=90°,如果∠A=30°,那么BC与斜边AB有什么关系?
C
B
A
D
取线段AB的中点D,连结CD,即CD为Rt△ABC斜边AB上的中线,则有CD=
AB=BD
由此可得出结论:
在直角三角形中,如果有一个锐角等于30°,那么它所对的直角边等于斜边的一半
你能用等边三角形的性质来证明直角三角形的
这条性质吗?
想一想
如图,在Rt△ABC中,如果BC=
AB,那么∠A等于多少度?
由此可得出结论:
在直角三角形中,如果一条直角边等于斜边的一半,那么这条直角边所对的角等于30°
例2
在A岛周围20海里(1海里=1852
m)水域内有暗礁,一轮船由西向东航行到O处时,发现A到在北偏东60°的方向,且与轮船相距
海里,如图所示.该船如果保持航向不变,有触礁的危险吗?
北
60°
如果三角形一边上的中线等于这条边的一半,求证:这个三角形是直角三角形
已知:CD是
△ABC的
AB边上的中线,且CD=
AB
求证:
△ABC是直角三角形
2.
如图,AC=AD,∠C,∠D是直角,将上述条件标注在图中,你能说明BC与BD相等吗?
C
D
A
B
解:在Rt△ACB和Rt△ADB中,则
AB=AB,
AC=AD.
∴
Rt△ACB≌Rt△ADB
(HL).
∴BC=BD
(全等三角形对应边相等).
2.
如图,两根长度为12米的绳子,一端系在旗杆上,另一端分别固定在地面两个木桩上,两个木桩离旗杆底部的距离相等吗?请说明你的理由.
所以Rt△ABD≌Rt△ACD(
HL
)
所以BD=CD
解:BD=CD
因为∠ADB=∠ADC=90°
在Rt△ABD和Rt△ACD中
AB=AC
AD=AD
在Rt△ABC中,
∠A
:∠B:
∠C
=1:2:3
,若AB=10cm,求BC的长
2.教材149页A组、B组
小结:这节课你有什么收获呢?与你的同伴进行交流
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
