11.1.2三角形的高、中线和角平分线 课件(27张ppt)
文档属性
| 名称 | 11.1.2三角形的高、中线和角平分线 课件(27张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-07 16:23:53 | ||
图片预览



文档简介
(共27张PPT)
第十一章
三角形
11.1.2
三角形的高、中线与角平分线
随堂演练
获取新知
知识回顾
例题讲解
课堂小结
知识回顾
定义
图示
垂线
线段中点
角平分线
O
B
A
A
B
当两条直线相交所成的四个角中,有一个角是直角时,就说这两条直线互相垂直,其中一条直线叫做另一条直线的垂线
把一条线段分成两条相等的线段的点
一条射线把一个角分成两个相等的角,这条射线叫做这个角的平分线
┐
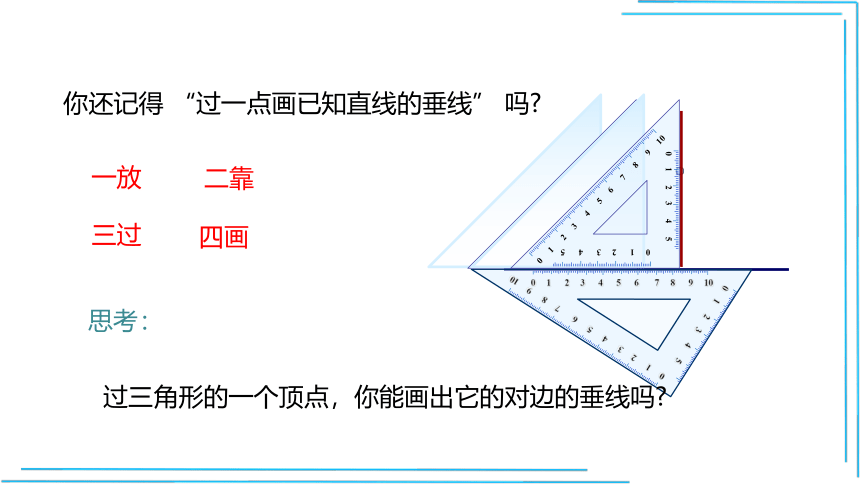
你还记得
“过一点画已知直线的垂线”
吗?
一放
二靠
三过
四画
0
1
2
3
4
5
0
1
2
3
4
5
6
7
8
9
10
0
1
2
3
4
5
6
7
8
9
10
0
1
2
3
4
5
6
7
8
9
10
0
1
2
3
4
5
0
1
2
3
4
5
0
1
2
3
4
5
6
7
8
9
10
0
1
2
3
4
5
0
1
2
3
4
5
0
1
2
3
4
5
6
7
8
9
10
0
1
2
3
4
5
0
1
2
3
4
5
思考:
过三角形的一个顶点,你能画出它的对边的垂线吗?
获取新知
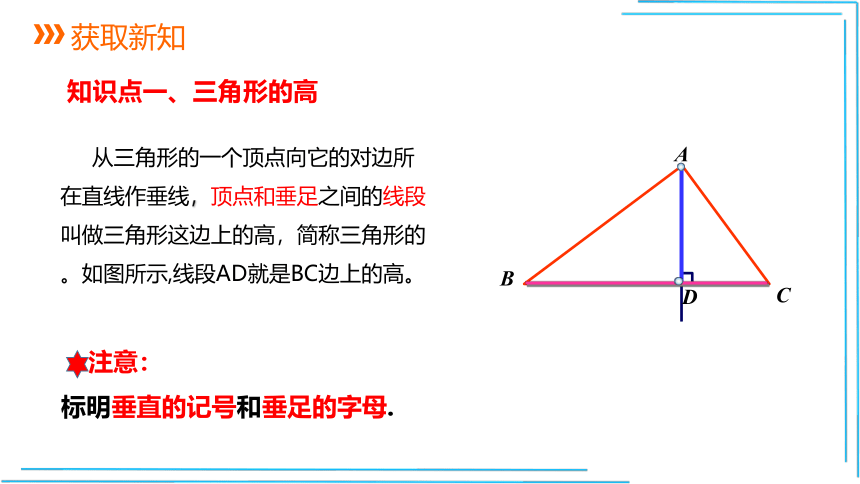
知识点一、三角形的高
从三角形的一个顶点向它的对边所在直线作垂线,顶点和垂足之间的线段叫做三角形这边上的高,简称三角形的。如图所示,线段AD就是BC边上的高。
A
B
C
D
注意:
标明垂直的记号和垂足的字母.
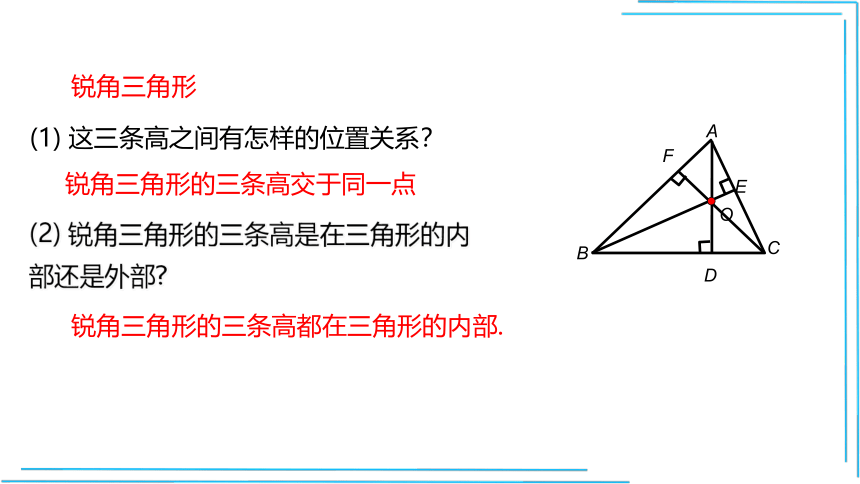
锐角三角形
D
E
F
O
A
B
C
(1)
这三条高之间有怎样的位置关系?
(2)
锐角三角形的三条高是在三角形的内部还是外部?
锐角三角形的三条高交于同一点
锐角三角形的三条高都在三角形的内部.
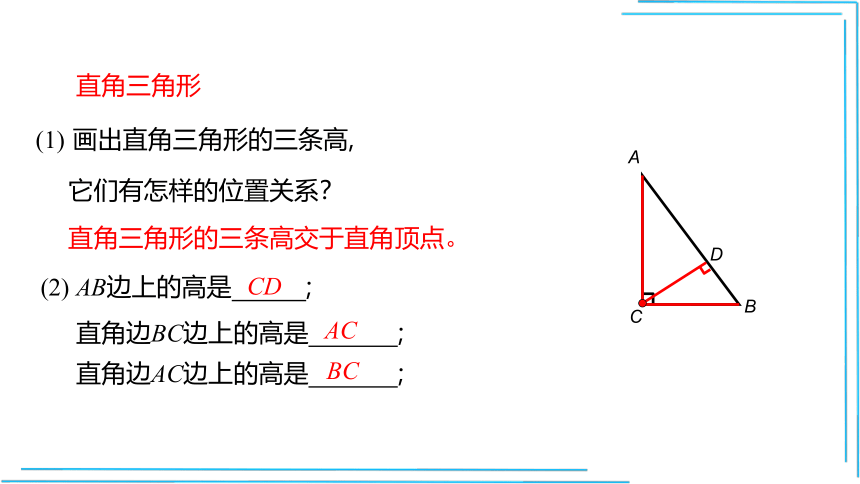
直角三角形
A
B
C
D
直角边BC边上的高是
;
直角边AC边上的高是
;
(2)
AB边上的高是
;
(1)
画出直角三角形的三条高,
它们有怎样的位置关系?
直角三角形的三条高交于直角顶点。
AC
BC
CD
????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????
????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????
????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????
????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????
????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????
????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????
????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????
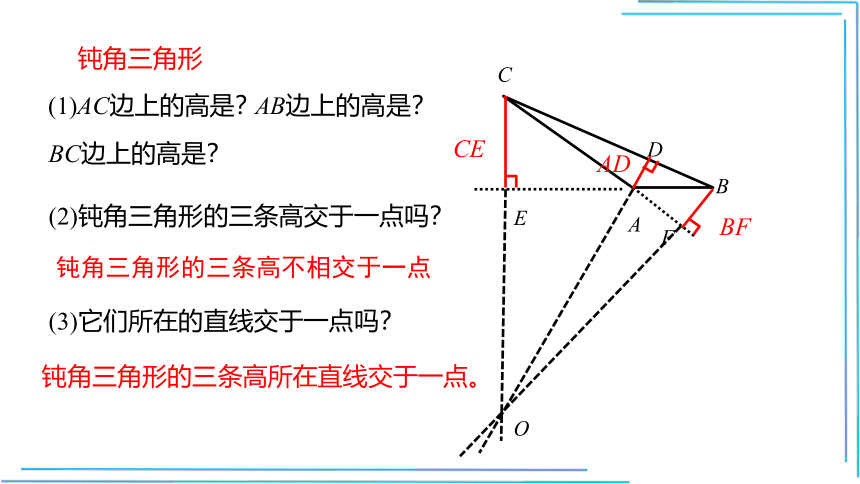
钝角三角形
A
B
C
D
E
F
O
(2)钝角三角形的三条高交于一点吗?
(3)它们所在的直线交于一点吗?
钝角三角形的三条高不相交于一点
钝角三角形的三条高所在直线交于一点。
(1)AC边上的高是?
AB边上的高是?
BC边上的高是?
BF
CE
AD
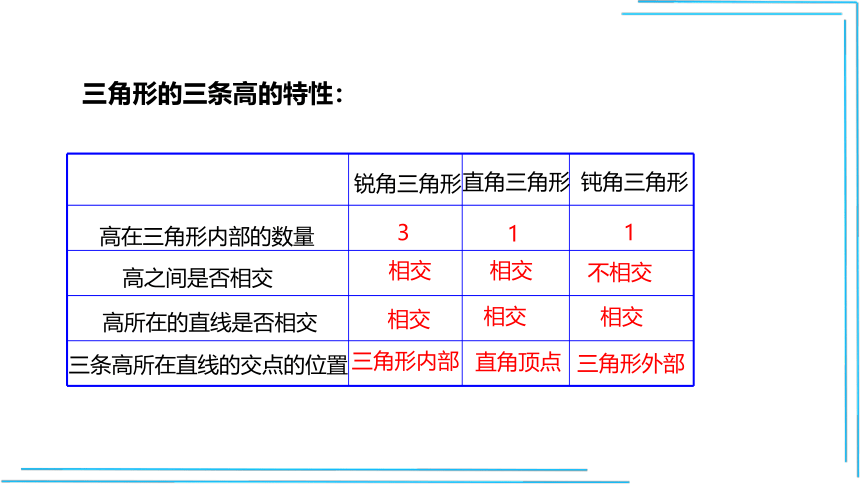
三角形的三条高的特性:
高所在的直线是否相交
高之间是否相交
高在三角形内部的数量
钝角三角形
直角三角形
锐角三角形
3
1
1
相交
相交
不相交
相交
相交
相交
三条高所在直线的交点的位置
三角形内部
直角顶点
三角形外部
例题讲解
例1
作△ABC的边AB上的高,下列作法中,正确的是( )
总结:三角形任意一边上的高必须满足:
(1)过该边所对的顶点;
(2)垂足必须在该边或在该边的延长线上.
D
知识点二、三角形的中线
如图
(1),连接△ABC的顶点A和它所对的边BC的中点D,
所得线段AD叫做
△ABC的边BC上的中线.
用同样方法,
你能画出△ABC
的另两条边上的中线吗?
锐角三角形
(1)
这三条中线之间有怎样的位置关系?
(2)
锐角三角形的三条中线是在三角
形的内部还是外部?
锐角三角形的三条中线交于同一点;
锐角三角形的三条中线都在三角形的内部.
直角三角形
钝角三角形
三角形的三条中线交于一点,这个交点就是三角形的重心.
中线有几条
中线之间是否相交
相交交点位置
中线在三角形内部的数量
钝角三角形
直角三角形
锐角三角形
3
3
3
相交
相交
相交
3
3
3
三角形内部
三角形内部
三角形内部
三角形的三条中线的特性:
例题讲解
例2
在△ABC中,AB=AC,AC边上的中线BD△ABC的周长分为12
cm和15
cm两部分,求△ABC的各边长.
解:设AB=x
cm,则AD=CD=
x
cm.
(1)如图①,若AB+AD=12
cm,则x+
x=12.解得x=8,
即AB=AC=8
cm,则CD=4
cm.故BC=15-4=11(cm).
此时AB+AC>BC,三角形存在,
所以三边长分别为8
cm,8
cm,11
cm.
(2)如图②,若AB+AD=15
cm,则x+
x=15.
解得x=10,即AB=AC=10
cm,则CD=5
cm.
故BC=12-5=7(cm).
显然此时三角形存在,所以三边长分别为10
cm,10
cm,
7
cm.
综上所述,△ABC的三边长分别为8
cm,8
cm,11
cm或10
cm,10
cm,7
cm.
知识点三、三角形的角平分线
在三角形中,一个内角的平分线与它的对边相交,这个角的顶点与交点之间的线段叫三角形的角平分线.如图所示,线段AD是△ABC的角平分线
1
2
A
C
D
∠1=∠2
B
注意:“三角形的角平分线”是一条线段.
三角形角平分线的性质
直角三角形
钝角三角形
锐角三角形
三角形的三条角平分线交于同一点.
例题讲解
例3
如图,已知AD是△ABC的角平分线,CE是△ABC的高,∠BAC=60°,∠BCE=40°,求∠ADB
的度数.
解:∵AD是△ABC的角平分线,∠BAC=60°,
∴∠DAC=∠BAD=30°.
∵CE是△ABC的高,∠BCE=40°,
∴∠B=50°,
∴∠ADB=180°-∠B-∠BAD
=180°-30°-50°=100°.
随堂演练
2.三角形一边上的中线把原三角形一定分成两个( )
A.形状相同的三角形
B.面积相等的三角形
C.直角三角形
D.周长相等的三角形
B
1.下列各组图形中,哪一组图形中AD是△ABC
的BC边上的高(
)
A
D
C
B
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
D
3.填空:
(1)如图①,AD,BE,CF是△ABC的三条中线,则
AB=
2__,BD=
__,AE=
__
AF
DC
AC
(2)如图②,AD,BE,CF是△ABC的三条角平分线,则∠1=
__,
∠3=_________,
∠ACB=2_____.
∠2
∠4
∠ABC
图①
图②
4.在ΔABC中,CD是中线,已知BC-AC=5cm,ΔDBC的周长为25cm,
求ΔADC的周长.
解:∵CD是△ABC的中线,
∴BD=AD,
∵△DBC的周长=BC+BD+CD=25cm,
∴BD+CD=25-BC.
∴△ADC的周长=AD+CD+AC
=BD+CD+AC
=25-BC+AC
=25-(BC-AC)=25-5=20cm.
A
D
B
C
思维拓展
如图,BE,CF均是△ABC的中线,且BE=CF,AM⊥CF于点M,AN⊥BE于点N.求证:AM=AN.
证明:∵BE,CF均是△ABC的中线,
∴
.
∵AM⊥CF,AN⊥BE,
∴
AM·CF=
AN·BE.
又∵BE=CF,
∴AM=AN.
知识归纳
三角形的
重要线段
概念
图形
表示法
三角形
的高线
从三角形的一个顶点向它的对边所在的直线作垂线,顶点和垂足之间的线段
∵AD是△ABC的高线.
∴AD⊥BC
∠ADB=∠ADC=90°.
三角形
的中线
三角形中,连结一个顶点和它对边中的线段
∵
AD是△ABC的BC上的中线.
∴
BD=CD=
BC.
三角形的
角平分线
三角形一个内角的平分线与它的对边相交,这个角顶点与交点之间的线段
∵.AD是△ABC的∠BAC的平分线
∴
∠1=∠2=
∠BAC
课堂小结
高
钝角三角形两短边上的高的画法
中线
会把原三角形面积平分
一边上的中线把原三角形分成两个三角形,这两个三角形的周长差等于原三角形其余两边的差
角平分线
三角形重要线段
https://www.21cnjy.com/help/help_extract.php
第十一章
三角形
11.1.2
三角形的高、中线与角平分线
随堂演练
获取新知
知识回顾
例题讲解
课堂小结
知识回顾
定义
图示
垂线
线段中点
角平分线
O
B
A
A
B
当两条直线相交所成的四个角中,有一个角是直角时,就说这两条直线互相垂直,其中一条直线叫做另一条直线的垂线
把一条线段分成两条相等的线段的点
一条射线把一个角分成两个相等的角,这条射线叫做这个角的平分线
┐
你还记得
“过一点画已知直线的垂线”
吗?
一放
二靠
三过
四画
0
1
2
3
4
5
0
1
2
3
4
5
6
7
8
9
10
0
1
2
3
4
5
6
7
8
9
10
0
1
2
3
4
5
6
7
8
9
10
0
1
2
3
4
5
0
1
2
3
4
5
0
1
2
3
4
5
6
7
8
9
10
0
1
2
3
4
5
0
1
2
3
4
5
0
1
2
3
4
5
6
7
8
9
10
0
1
2
3
4
5
0
1
2
3
4
5
思考:
过三角形的一个顶点,你能画出它的对边的垂线吗?
获取新知
知识点一、三角形的高
从三角形的一个顶点向它的对边所在直线作垂线,顶点和垂足之间的线段叫做三角形这边上的高,简称三角形的。如图所示,线段AD就是BC边上的高。
A
B
C
D
注意:
标明垂直的记号和垂足的字母.
锐角三角形
D
E
F
O
A
B
C
(1)
这三条高之间有怎样的位置关系?
(2)
锐角三角形的三条高是在三角形的内部还是外部?
锐角三角形的三条高交于同一点
锐角三角形的三条高都在三角形的内部.
直角三角形
A
B
C
D
直角边BC边上的高是
;
直角边AC边上的高是
;
(2)
AB边上的高是
;
(1)
画出直角三角形的三条高,
它们有怎样的位置关系?
直角三角形的三条高交于直角顶点。
AC
BC
CD
????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????
????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????
????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????
????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????
????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????
????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????
????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????
钝角三角形
A
B
C
D
E
F
O
(2)钝角三角形的三条高交于一点吗?
(3)它们所在的直线交于一点吗?
钝角三角形的三条高不相交于一点
钝角三角形的三条高所在直线交于一点。
(1)AC边上的高是?
AB边上的高是?
BC边上的高是?
BF
CE
AD
三角形的三条高的特性:
高所在的直线是否相交
高之间是否相交
高在三角形内部的数量
钝角三角形
直角三角形
锐角三角形
3
1
1
相交
相交
不相交
相交
相交
相交
三条高所在直线的交点的位置
三角形内部
直角顶点
三角形外部
例题讲解
例1
作△ABC的边AB上的高,下列作法中,正确的是( )
总结:三角形任意一边上的高必须满足:
(1)过该边所对的顶点;
(2)垂足必须在该边或在该边的延长线上.
D
知识点二、三角形的中线
如图
(1),连接△ABC的顶点A和它所对的边BC的中点D,
所得线段AD叫做
△ABC的边BC上的中线.
用同样方法,
你能画出△ABC
的另两条边上的中线吗?
锐角三角形
(1)
这三条中线之间有怎样的位置关系?
(2)
锐角三角形的三条中线是在三角
形的内部还是外部?
锐角三角形的三条中线交于同一点;
锐角三角形的三条中线都在三角形的内部.
直角三角形
钝角三角形
三角形的三条中线交于一点,这个交点就是三角形的重心.
中线有几条
中线之间是否相交
相交交点位置
中线在三角形内部的数量
钝角三角形
直角三角形
锐角三角形
3
3
3
相交
相交
相交
3
3
3
三角形内部
三角形内部
三角形内部
三角形的三条中线的特性:
例题讲解
例2
在△ABC中,AB=AC,AC边上的中线BD△ABC的周长分为12
cm和15
cm两部分,求△ABC的各边长.
解:设AB=x
cm,则AD=CD=
x
cm.
(1)如图①,若AB+AD=12
cm,则x+
x=12.解得x=8,
即AB=AC=8
cm,则CD=4
cm.故BC=15-4=11(cm).
此时AB+AC>BC,三角形存在,
所以三边长分别为8
cm,8
cm,11
cm.
(2)如图②,若AB+AD=15
cm,则x+
x=15.
解得x=10,即AB=AC=10
cm,则CD=5
cm.
故BC=12-5=7(cm).
显然此时三角形存在,所以三边长分别为10
cm,10
cm,
7
cm.
综上所述,△ABC的三边长分别为8
cm,8
cm,11
cm或10
cm,10
cm,7
cm.
知识点三、三角形的角平分线
在三角形中,一个内角的平分线与它的对边相交,这个角的顶点与交点之间的线段叫三角形的角平分线.如图所示,线段AD是△ABC的角平分线
1
2
A
C
D
∠1=∠2
B
注意:“三角形的角平分线”是一条线段.
三角形角平分线的性质
直角三角形
钝角三角形
锐角三角形
三角形的三条角平分线交于同一点.
例题讲解
例3
如图,已知AD是△ABC的角平分线,CE是△ABC的高,∠BAC=60°,∠BCE=40°,求∠ADB
的度数.
解:∵AD是△ABC的角平分线,∠BAC=60°,
∴∠DAC=∠BAD=30°.
∵CE是△ABC的高,∠BCE=40°,
∴∠B=50°,
∴∠ADB=180°-∠B-∠BAD
=180°-30°-50°=100°.
随堂演练
2.三角形一边上的中线把原三角形一定分成两个( )
A.形状相同的三角形
B.面积相等的三角形
C.直角三角形
D.周长相等的三角形
B
1.下列各组图形中,哪一组图形中AD是△ABC
的BC边上的高(
)
A
D
C
B
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
D
3.填空:
(1)如图①,AD,BE,CF是△ABC的三条中线,则
AB=
2__,BD=
__,AE=
__
AF
DC
AC
(2)如图②,AD,BE,CF是△ABC的三条角平分线,则∠1=
__,
∠3=_________,
∠ACB=2_____.
∠2
∠4
∠ABC
图①
图②
4.在ΔABC中,CD是中线,已知BC-AC=5cm,ΔDBC的周长为25cm,
求ΔADC的周长.
解:∵CD是△ABC的中线,
∴BD=AD,
∵△DBC的周长=BC+BD+CD=25cm,
∴BD+CD=25-BC.
∴△ADC的周长=AD+CD+AC
=BD+CD+AC
=25-BC+AC
=25-(BC-AC)=25-5=20cm.
A
D
B
C
思维拓展
如图,BE,CF均是△ABC的中线,且BE=CF,AM⊥CF于点M,AN⊥BE于点N.求证:AM=AN.
证明:∵BE,CF均是△ABC的中线,
∴
.
∵AM⊥CF,AN⊥BE,
∴
AM·CF=
AN·BE.
又∵BE=CF,
∴AM=AN.
知识归纳
三角形的
重要线段
概念
图形
表示法
三角形
的高线
从三角形的一个顶点向它的对边所在的直线作垂线,顶点和垂足之间的线段
∵AD是△ABC的高线.
∴AD⊥BC
∠ADB=∠ADC=90°.
三角形
的中线
三角形中,连结一个顶点和它对边中的线段
∵
AD是△ABC的BC上的中线.
∴
BD=CD=
BC.
三角形的
角平分线
三角形一个内角的平分线与它的对边相交,这个角顶点与交点之间的线段
∵.AD是△ABC的∠BAC的平分线
∴
∠1=∠2=
∠BAC
课堂小结
高
钝角三角形两短边上的高的画法
中线
会把原三角形面积平分
一边上的中线把原三角形分成两个三角形,这两个三角形的周长差等于原三角形其余两边的差
角平分线
三角形重要线段
https://www.21cnjy.com/help/help_extract.php
