11.2.1三角形的内角和 第1课时 课件 (共23张PPT)
文档属性
| 名称 | 11.2.1三角形的内角和 第1课时 课件 (共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-07 17:42:29 | ||
图片预览




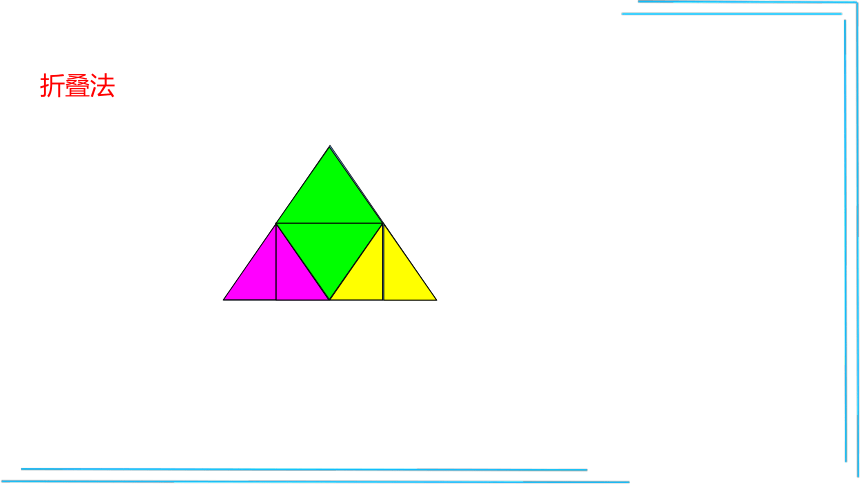
文档简介
(共23张PPT)
第十一章
三角形
11.2.1
第1课时
三角形的内角和
随堂演练
获取新知
情境导入
例题讲解
课堂小结
情境导入
问题1 在小学我们已经知道任意一个三角形三个内角的和等于180°,你还记得是怎么发现这个结论的吗?请大家利用手中的三角形纸片进行探究.
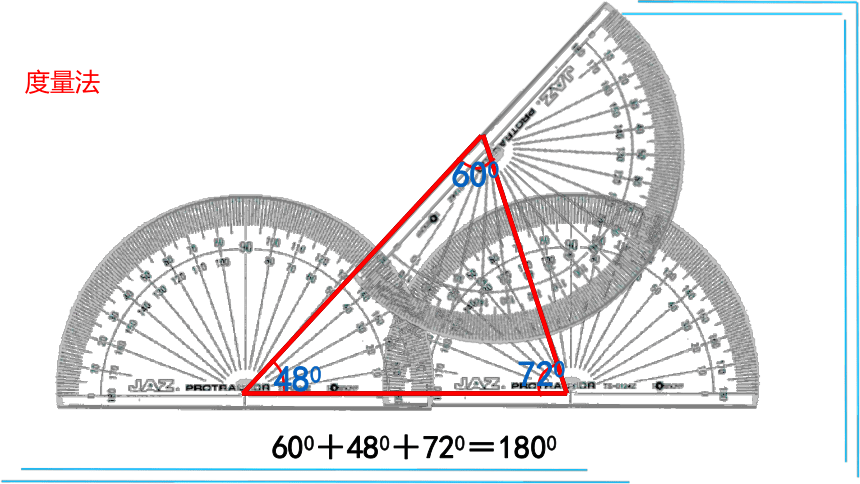
度量法
600+480+720=1800
480
720
600
折叠法
A
B
C
2
1
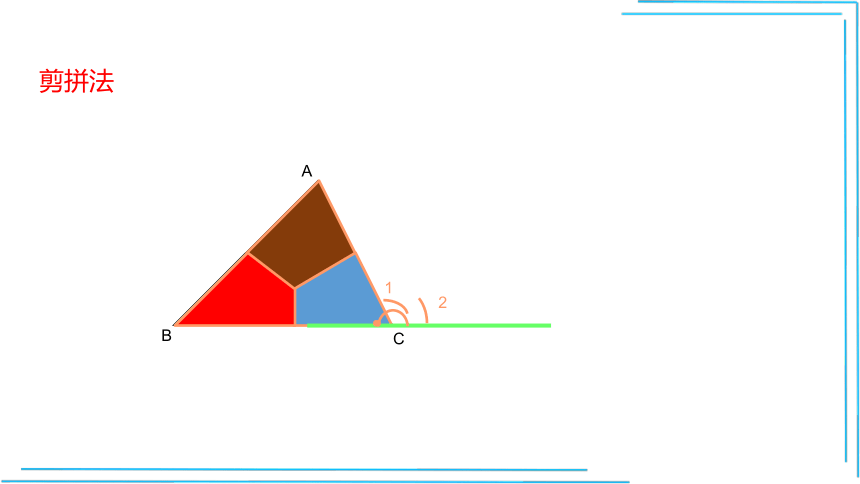
剪拼法
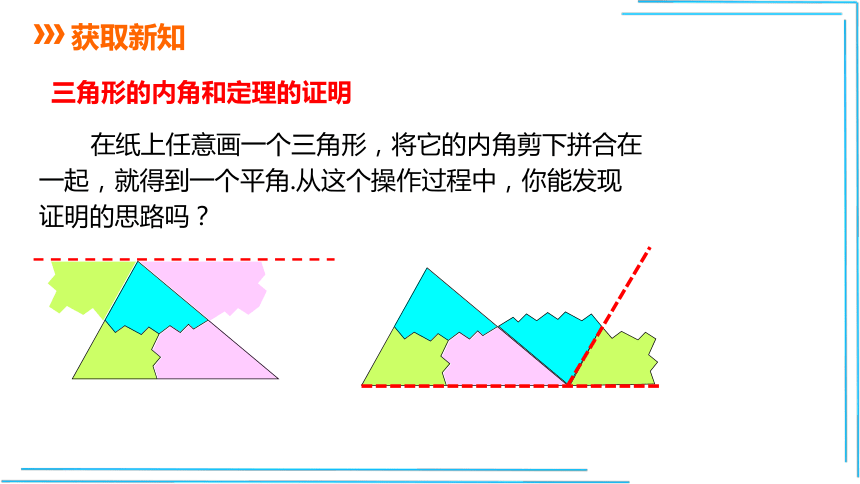
三角形的内角和定理的证明
在纸上任意画一个三角形,将它的内角剪下拼合在
一起,就得到一个平角.从这个操作过程中,你能发现
证明的思路吗?
获取新知
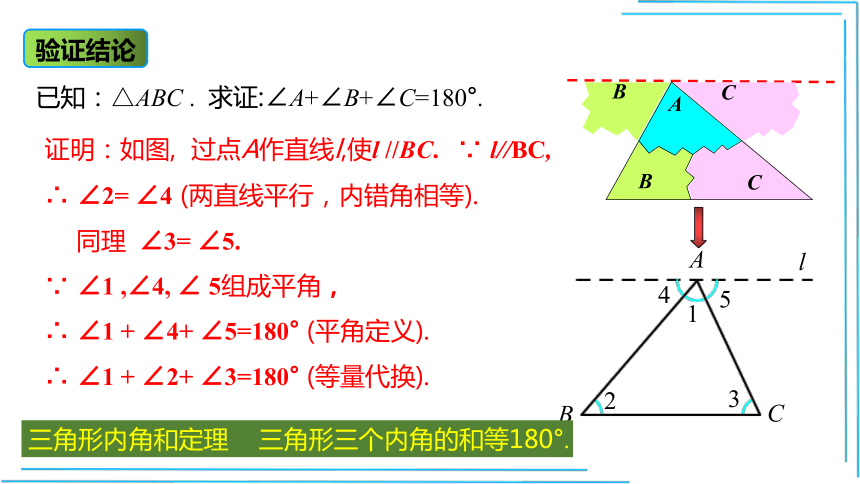
已知:△ABC
.
求证:∠A+∠B+∠C=180°.
A
B
C
2
4
1
5
3
l
证明:如图,
过点A作直线l,使l
//BC.
∵
l//BC,
∴
∠2=
∠4
(两直线平行,内错角相等).
同理
∠3=
∠5.
∵
∠1
,∠4,
∠
5组成平角,
∴
∠1
+
∠4+
∠5=180°
(平角定义).
∴
∠1
+
∠2+
∠3=180°
(等量代换).
三角形内角和定理
三角形三个内角的和等180°.
验证结论
A
B
C
B
C
证法2:
延长BC到D,过点C作CE∥BA,
∴
∠A=∠1
.
(两直线平行,内错角相等)
∠B=∠2.
(两直线平行,同位角相等)
又∵∠1+∠2+∠ACB=180°,
∴∠A+∠B+∠ACB=180°.
E
D
1
2
C
B
A
A
B
C
A
B
C
B
A
E
D
F
关键是通过“平移”将分散的聚集在一起“转化”为一个平角
A
B
C
D
E
C
A
B
1
2
3
4
5
l
在这里,为了证明的需要,在原来的图形上添画的线叫做辅助线.在平面几何里,辅助线通常画成虚线.
思路总结
为了证明三个角的和为180°,转化为一个平角或同旁内角互补等,这种转化思想是数学中的常用方法.
作辅助线
例题讲解
例1
如图
,在△ABC
中,∠BAC
=40°,∠B
=
75°,
AD是△
ABC的角平分线.求
∠ADB
的度数.
C
B
D
A
解:由∠BAC=40°,AD是△
ABC的角平分线,
得∠BAD=
∠BAC=20°.
在△
ABD中,
∠ADB
=180°-∠B-∠BAD
=
180°
-
75°-
20°=85°.
例2
下图是A,B,C三岛的平面图,
C岛在A岛的北偏东50°方向,B岛在A岛的北
偏东80°方向,C岛在B岛的北偏西40°方向。从B岛看A,C两岛的视角∠ABC是多少度?从C岛
看A,
B两岛的视角∠
ACB呢?
北
北
C
A
B
D
E
分析:A,B,C三岛的连线构成
ABC,
所求的∠ACB是△ABC的一个内角.如果能求出∠
CAB,
∠
ABC,就能求出∠ACB.
解:∠CAB=∠BAD
-
∠CAD=80°-
50°=30°.
由
AD//BE,得
∠
BAD
+∠
ABE=180°.
所以∠
ABE=180°-
∠BAD
=
180°-
80°=
100°,
∠
ABC=∠
ABE
-
∠EBC=100°
-
40°=60°.
在△ABC中,
∠
ACB
=180°
-
∠ABC
-
∠
CAB
=
180°
-
60°
-
30°=90°.
答:从B岛看A,
C两岛的视角∠
ABC是60°,
从C岛看A,
B两岛的视角∠
ACB是90°.
北
北
C
A
B
D
E
你能想出一个更简捷的方法来求∠C的度数吗?
方法二:
B
D
C
E
北
A
1
2
50°
解:过点C画CF∥AD
∴
∠1=∠DAC=50
°,
∵
CF∥AD,
又AD
∥BE,
∴
CF∥
BE,
∴∠2=∠CBE
=40
°
∴
∠ACB=∠1
+
∠2
=50
°
+
40
°
=90
°
F
随堂演练
1.下列各组角中,属于同一个三角形的内角的是( )
A.95°,75°,10°
B.60°,73°,67°
C.34°,36°,50°
D.25°,160°,15°
A
2.在△ABC中,∠A
:∠B:∠C=1:2:3,则△ABC是_____三角形
.
直角
3.在△ABC中∠A=
∠B+10°,
∠C=
∠A
+
10°,
则∠A=
,
∠B=
,∠
C=
.
60°
50°
70°
4.已知:如图所示,可求出∠1=
°,?∠2=
°,∠3=
°.?
60
35
90
5.在△ABC
中,
∠A
的度数是∠B
的度数的3倍,∠C
比∠B
大15°,求∠A,∠B,∠C的度数.
解:
设∠B为x°,则∠A为(3x)°,
∠C为(x
+
15)°,
从而有
3x
+
x
+(x
+
15)=
180.
解得
x
=
33.
所以
3x
=
99
,
x
+
15
=
48.
答:
∠A,
∠B,
∠C的度数分别为99°,
33°,
48°.
几何问题借助方程来解.
这是一个重要的数学思想.
思维拓展
如图,在△ABC中,BP平分∠ABC,CP平分∠ACB,写出∠BPC与∠A
之间的数量关系.
解:∵BP平分∠ABC,CP平分∠ACB,
∴∠PBC+∠PCB=
(∠ABC+∠ACB)=60°.
∵∠PBC+∠PCB+∠BPC=180°,
∴∠BPC=180°-
(∠ABC+∠ACB)
=180°-
(180°-∠A)=90°+
∠A
.
课堂小结
求角度
证法
应用
转化为一个平角
或同旁内角互补
三角形的
内角和等
于180
°
辅助线
https://www.21cnjy.com/help/help_extract.php
第十一章
三角形
11.2.1
第1课时
三角形的内角和
随堂演练
获取新知
情境导入
例题讲解
课堂小结
情境导入
问题1 在小学我们已经知道任意一个三角形三个内角的和等于180°,你还记得是怎么发现这个结论的吗?请大家利用手中的三角形纸片进行探究.
度量法
600+480+720=1800
480
720
600
折叠法
A
B
C
2
1
剪拼法
三角形的内角和定理的证明
在纸上任意画一个三角形,将它的内角剪下拼合在
一起,就得到一个平角.从这个操作过程中,你能发现
证明的思路吗?
获取新知
已知:△ABC
.
求证:∠A+∠B+∠C=180°.
A
B
C
2
4
1
5
3
l
证明:如图,
过点A作直线l,使l
//BC.
∵
l//BC,
∴
∠2=
∠4
(两直线平行,内错角相等).
同理
∠3=
∠5.
∵
∠1
,∠4,
∠
5组成平角,
∴
∠1
+
∠4+
∠5=180°
(平角定义).
∴
∠1
+
∠2+
∠3=180°
(等量代换).
三角形内角和定理
三角形三个内角的和等180°.
验证结论
A
B
C
B
C
证法2:
延长BC到D,过点C作CE∥BA,
∴
∠A=∠1
.
(两直线平行,内错角相等)
∠B=∠2.
(两直线平行,同位角相等)
又∵∠1+∠2+∠ACB=180°,
∴∠A+∠B+∠ACB=180°.
E
D
1
2
C
B
A
A
B
C
A
B
C
B
A
E
D
F
关键是通过“平移”将分散的聚集在一起“转化”为一个平角
A
B
C
D
E
C
A
B
1
2
3
4
5
l
在这里,为了证明的需要,在原来的图形上添画的线叫做辅助线.在平面几何里,辅助线通常画成虚线.
思路总结
为了证明三个角的和为180°,转化为一个平角或同旁内角互补等,这种转化思想是数学中的常用方法.
作辅助线
例题讲解
例1
如图
,在△ABC
中,∠BAC
=40°,∠B
=
75°,
AD是△
ABC的角平分线.求
∠ADB
的度数.
C
B
D
A
解:由∠BAC=40°,AD是△
ABC的角平分线,
得∠BAD=
∠BAC=20°.
在△
ABD中,
∠ADB
=180°-∠B-∠BAD
=
180°
-
75°-
20°=85°.
例2
下图是A,B,C三岛的平面图,
C岛在A岛的北偏东50°方向,B岛在A岛的北
偏东80°方向,C岛在B岛的北偏西40°方向。从B岛看A,C两岛的视角∠ABC是多少度?从C岛
看A,
B两岛的视角∠
ACB呢?
北
北
C
A
B
D
E
分析:A,B,C三岛的连线构成
ABC,
所求的∠ACB是△ABC的一个内角.如果能求出∠
CAB,
∠
ABC,就能求出∠ACB.
解:∠CAB=∠BAD
-
∠CAD=80°-
50°=30°.
由
AD//BE,得
∠
BAD
+∠
ABE=180°.
所以∠
ABE=180°-
∠BAD
=
180°-
80°=
100°,
∠
ABC=∠
ABE
-
∠EBC=100°
-
40°=60°.
在△ABC中,
∠
ACB
=180°
-
∠ABC
-
∠
CAB
=
180°
-
60°
-
30°=90°.
答:从B岛看A,
C两岛的视角∠
ABC是60°,
从C岛看A,
B两岛的视角∠
ACB是90°.
北
北
C
A
B
D
E
你能想出一个更简捷的方法来求∠C的度数吗?
方法二:
B
D
C
E
北
A
1
2
50°
解:过点C画CF∥AD
∴
∠1=∠DAC=50
°,
∵
CF∥AD,
又AD
∥BE,
∴
CF∥
BE,
∴∠2=∠CBE
=40
°
∴
∠ACB=∠1
+
∠2
=50
°
+
40
°
=90
°
F
随堂演练
1.下列各组角中,属于同一个三角形的内角的是( )
A.95°,75°,10°
B.60°,73°,67°
C.34°,36°,50°
D.25°,160°,15°
A
2.在△ABC中,∠A
:∠B:∠C=1:2:3,则△ABC是_____三角形
.
直角
3.在△ABC中∠A=
∠B+10°,
∠C=
∠A
+
10°,
则∠A=
,
∠B=
,∠
C=
.
60°
50°
70°
4.已知:如图所示,可求出∠1=
°,?∠2=
°,∠3=
°.?
60
35
90
5.在△ABC
中,
∠A
的度数是∠B
的度数的3倍,∠C
比∠B
大15°,求∠A,∠B,∠C的度数.
解:
设∠B为x°,则∠A为(3x)°,
∠C为(x
+
15)°,
从而有
3x
+
x
+(x
+
15)=
180.
解得
x
=
33.
所以
3x
=
99
,
x
+
15
=
48.
答:
∠A,
∠B,
∠C的度数分别为99°,
33°,
48°.
几何问题借助方程来解.
这是一个重要的数学思想.
思维拓展
如图,在△ABC中,BP平分∠ABC,CP平分∠ACB,写出∠BPC与∠A
之间的数量关系.
解:∵BP平分∠ABC,CP平分∠ACB,
∴∠PBC+∠PCB=
(∠ABC+∠ACB)=60°.
∵∠PBC+∠PCB+∠BPC=180°,
∴∠BPC=180°-
(∠ABC+∠ACB)
=180°-
(180°-∠A)=90°+
∠A
.
课堂小结
求角度
证法
应用
转化为一个平角
或同旁内角互补
三角形的
内角和等
于180
°
辅助线
https://www.21cnjy.com/help/help_extract.php
