11.2.2三角形的外角 课件 (共22张PPT)
文档属性
| 名称 | 11.2.2三角形的外角 课件 (共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-07 17:47:07 | ||
图片预览



文档简介
(共22张PPT)
第十一章
三角形
11.2.2
三角形的外角
随堂演练
获取新知
情境导入
例题讲解
课堂小结
情境导入
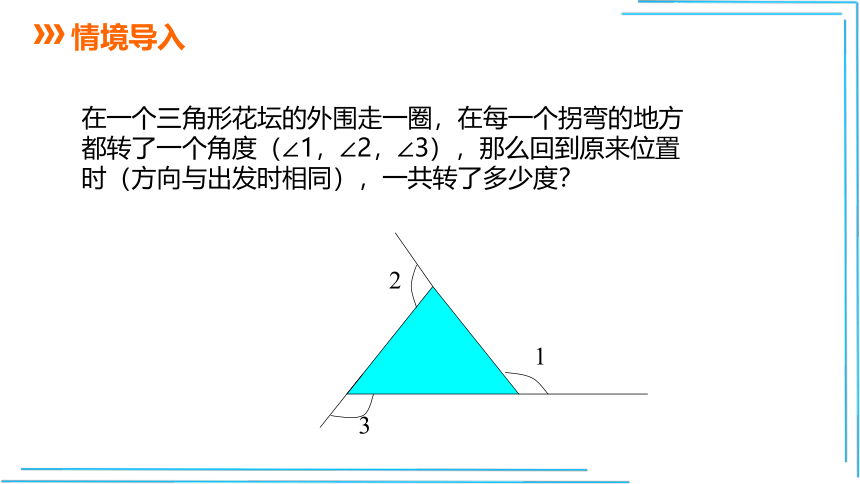
在一个三角形花坛的外围走一圈,在每一个拐弯的地方都转了一个角度(∠1,∠2,∠3),那么回到原来位置时(方向与出发时相同),一共转了多少度?
1
2
3
获取新知
三角形的一边与另一边的延长线组成的角,叫做三角形的外角.
(∠1,即∠BCD是△ABC的外角)
知识点一:三角形的外角
B
A
1
D
C
外角
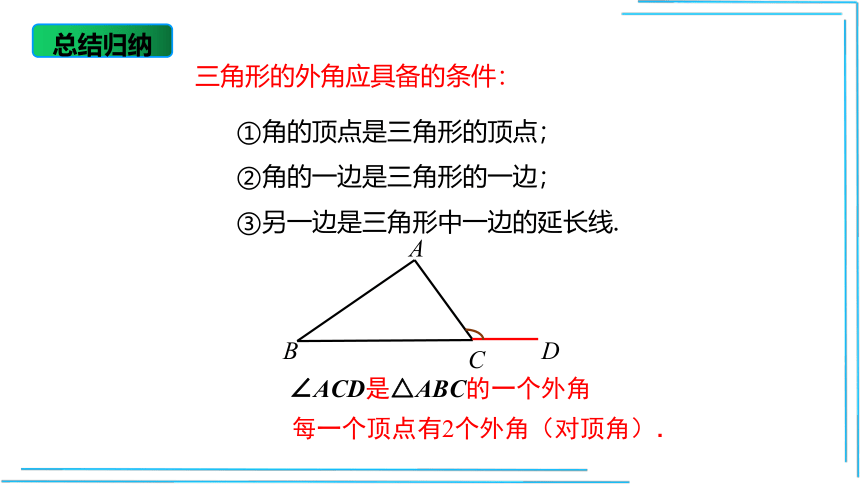
三角形的外角应具备的条件:
①角的顶点是三角形的顶点;
②角的一边是三角形的一边;
③另一边是三角形中一边的延长线.
∠ACD是△ABC的一个外角
C
B
A
D
每一个顶点有2个外角(对顶角).
总结归纳
F
A
B
C
D
E
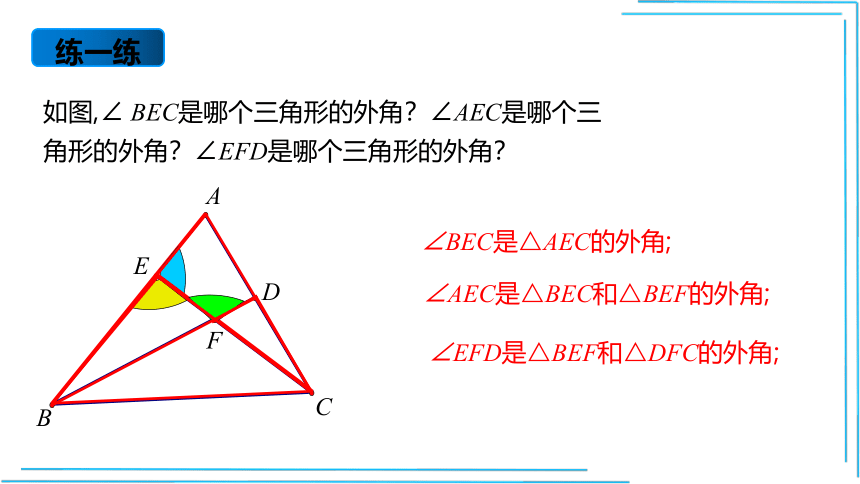
∠BEC是△AEC的外角;
∠AEC是△BEC和△BEF的外角;
如图,∠
BEC是哪个三角形的外角?∠AEC是哪个三角形的外角?∠EFD是哪个三角形的外角?
练一练
∠EFD是△BEF和△DFC的外角;
知识点二:三角形外角的性质
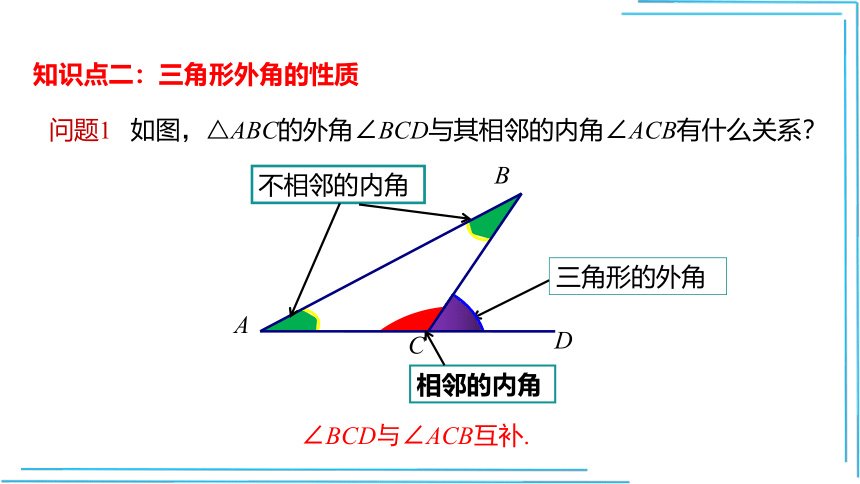
问题1
如图,△ABC的外角∠BCD与其相邻的内角∠ACB有什么关系?
三角形的外角
A
C
B
D
相邻的内角
不相邻的内角
∠BCD与∠ACB互补.
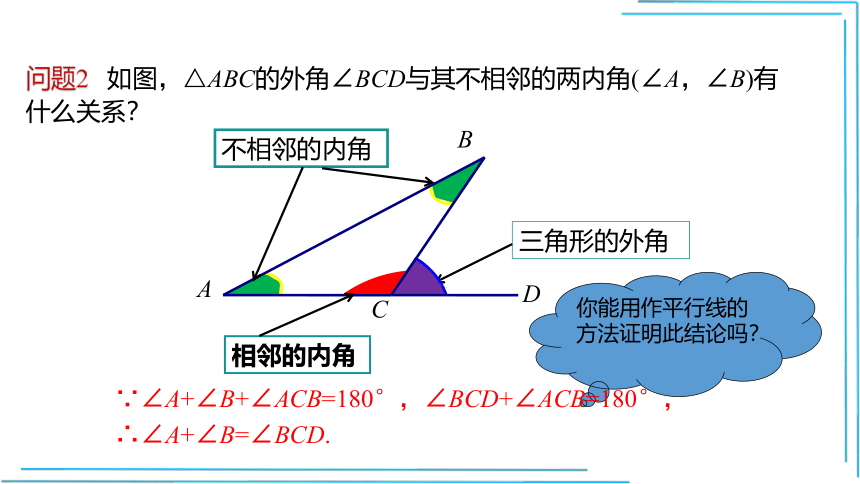
问题2
如图,△ABC的外角∠BCD与其不相邻的两内角(∠A,∠B)有什么关系?
三角形的外角
A
C
B
D
相邻的内角
不相邻的内角
你能用作平行线的方法证明此结论吗?
∵∠A+∠B+∠ACB=180°,∠BCD+∠ACB=180°,
∴∠A+∠B=∠BCD.
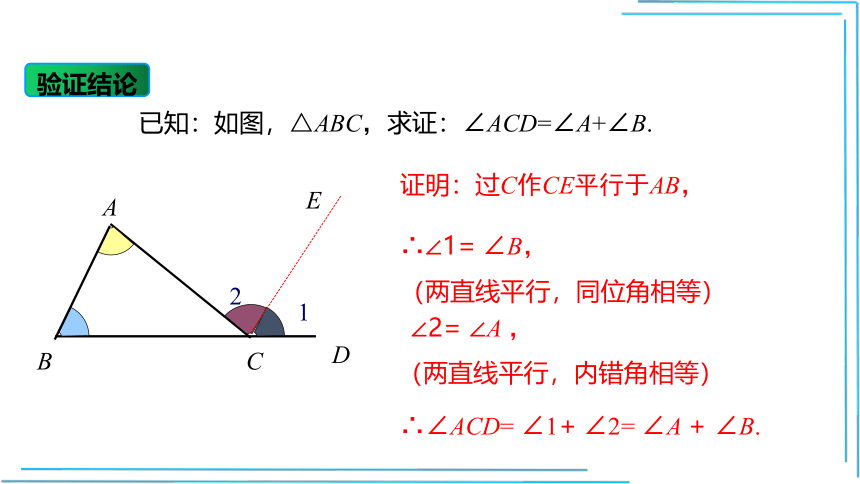
已知:如图,△ABC,求证:∠ACD=∠A+∠B.
B
C
1
2
E
A
验证结论
证明:过C作CE平行于AB,
∴∠1=
∠B,
(两直线平行,同位角相等)
∠2=
∠A
,
(两直线平行,内错角相等)
∴∠ACD=
∠1+
∠2=
∠A
+
∠B.
D
三角形内角和定理的推论:
A
B
C
D
(
(
(
三角形的外角等于与它不相邻的两个内角的和.
几何语言:
∵
∠ACD是△ABC的一个外角
∴
∠ACD=
∠A+
∠B.
知识要点
求下列各图中∠1的度数.
30°
60°
1
35°
120°
1
45°
50°
1
90°
85°
练一练
例题讲解
例1
[教材补充例题]如图11-2-9,在△ABC中,已知D是边BC上的一点,且∠ADE=∠B,那么∠1与∠2相等吗?为什么?
图11-2-9
解:∠1=∠2.理由:
因为∠ADC=∠B+∠1,
∠ADC=∠ADE+∠2,
所以∠B+∠1=∠ADE+∠2.
又因为∠ADE=∠B,
所以∠1=∠2.
三角形外角的性质常见的两个应用
(1)已知三角形的两个内角,求与这两个内角不相邻的外角;
(2)已知三角形的一个外角和与其不相邻的一个内角,求另一
个与其不相邻的内角.
A
B
C
1
2
3
知识点三:三角形的外角和
∠1+∠2
+∠3
=
?
(每个顶点取一个外角)
∠2+
∠ABC=180°,
∠3+
∠ACB=180°,
三个式子相加得到
∠1+∠2+∠3+∠BAC+∠ABC+∠ACB=540°,
而∠BAC+
∠ABC+∠ACB=180°,
故∠1+
∠2+
∠3=360°.
方法一:∠1+
∠BAC=180°,
解:
A
B
C
1
2
3
解:方法二:过A作AD平行于BC,
B
C
1
2
3
4
A
∠3=∠4,
∠2=∠BAD,
所以,
∠1+
∠2+
∠3=
∠1+
∠4+
∠BAD=360°.
D
∠2+
∠
3=
∠
4+∠BAD,
两直线平行,同位角相等
结论:三角形的外角和等于360°.
判断题:
1.三角形的外角和是指三角形所有外角的和.(
)
2.三角形的外角和等于它内角和的2倍.(
)
3.三角形的一个外角等于两个内角的和.(
)
练一练
1.图D-6-1中是△ABC的外角的是( )
A.∠EAB和∠EAD
B.∠EAB和∠DAC
C.∠EAB和∠EAD,∠DAC
D.以上说法都不对
B
图D-6-1
2.如图D-6-2,∠ACD是△ABC的外角,CE平分∠ACD,
若∠A=60°,∠B=40°,则∠ECD等于( )
A.40°
B.45°
C.50°
D.55°
C
随堂演练
图D-6-2
3
.如图,D是△ABC的BC边上一点,∠B=∠BAD,
∠ADC=80°,∠BAC=70°,求:(1)∠B
的度数;(2)∠C的度数.
C
D
解:因为∠ADC是△ABD的外角.
在△ABC中,
因为∠B+∠BAC+∠C=180°,
所以∠C=180?-∠B-∠BAC
=180?-40?-70?=70°.
所以∠ADC=∠B+∠BAD=80°.
又因为∠B=∠BAD,
B
A
课堂小结
三角形的外角
定义
角一边必须是三角形的一边,另一边必须是三角形另一边的延长线
性质
三角形的一个外角等于与它不相邻的两个内角的和
三角形的外角和
三角形的外角和等于360
°
https://www.21cnjy.com/help/help_extract.php
第十一章
三角形
11.2.2
三角形的外角
随堂演练
获取新知
情境导入
例题讲解
课堂小结
情境导入
在一个三角形花坛的外围走一圈,在每一个拐弯的地方都转了一个角度(∠1,∠2,∠3),那么回到原来位置时(方向与出发时相同),一共转了多少度?
1
2
3
获取新知
三角形的一边与另一边的延长线组成的角,叫做三角形的外角.
(∠1,即∠BCD是△ABC的外角)
知识点一:三角形的外角
B
A
1
D
C
外角
三角形的外角应具备的条件:
①角的顶点是三角形的顶点;
②角的一边是三角形的一边;
③另一边是三角形中一边的延长线.
∠ACD是△ABC的一个外角
C
B
A
D
每一个顶点有2个外角(对顶角).
总结归纳
F
A
B
C
D
E
∠BEC是△AEC的外角;
∠AEC是△BEC和△BEF的外角;
如图,∠
BEC是哪个三角形的外角?∠AEC是哪个三角形的外角?∠EFD是哪个三角形的外角?
练一练
∠EFD是△BEF和△DFC的外角;
知识点二:三角形外角的性质
问题1
如图,△ABC的外角∠BCD与其相邻的内角∠ACB有什么关系?
三角形的外角
A
C
B
D
相邻的内角
不相邻的内角
∠BCD与∠ACB互补.
问题2
如图,△ABC的外角∠BCD与其不相邻的两内角(∠A,∠B)有什么关系?
三角形的外角
A
C
B
D
相邻的内角
不相邻的内角
你能用作平行线的方法证明此结论吗?
∵∠A+∠B+∠ACB=180°,∠BCD+∠ACB=180°,
∴∠A+∠B=∠BCD.
已知:如图,△ABC,求证:∠ACD=∠A+∠B.
B
C
1
2
E
A
验证结论
证明:过C作CE平行于AB,
∴∠1=
∠B,
(两直线平行,同位角相等)
∠2=
∠A
,
(两直线平行,内错角相等)
∴∠ACD=
∠1+
∠2=
∠A
+
∠B.
D
三角形内角和定理的推论:
A
B
C
D
(
(
(
三角形的外角等于与它不相邻的两个内角的和.
几何语言:
∵
∠ACD是△ABC的一个外角
∴
∠ACD=
∠A+
∠B.
知识要点
求下列各图中∠1的度数.
30°
60°
1
35°
120°
1
45°
50°
1
90°
85°
练一练
例题讲解
例1
[教材补充例题]如图11-2-9,在△ABC中,已知D是边BC上的一点,且∠ADE=∠B,那么∠1与∠2相等吗?为什么?
图11-2-9
解:∠1=∠2.理由:
因为∠ADC=∠B+∠1,
∠ADC=∠ADE+∠2,
所以∠B+∠1=∠ADE+∠2.
又因为∠ADE=∠B,
所以∠1=∠2.
三角形外角的性质常见的两个应用
(1)已知三角形的两个内角,求与这两个内角不相邻的外角;
(2)已知三角形的一个外角和与其不相邻的一个内角,求另一
个与其不相邻的内角.
A
B
C
1
2
3
知识点三:三角形的外角和
∠1+∠2
+∠3
=
?
(每个顶点取一个外角)
∠2+
∠ABC=180°,
∠3+
∠ACB=180°,
三个式子相加得到
∠1+∠2+∠3+∠BAC+∠ABC+∠ACB=540°,
而∠BAC+
∠ABC+∠ACB=180°,
故∠1+
∠2+
∠3=360°.
方法一:∠1+
∠BAC=180°,
解:
A
B
C
1
2
3
解:方法二:过A作AD平行于BC,
B
C
1
2
3
4
A
∠3=∠4,
∠2=∠BAD,
所以,
∠1+
∠2+
∠3=
∠1+
∠4+
∠BAD=360°.
D
∠2+
∠
3=
∠
4+∠BAD,
两直线平行,同位角相等
结论:三角形的外角和等于360°.
判断题:
1.三角形的外角和是指三角形所有外角的和.(
)
2.三角形的外角和等于它内角和的2倍.(
)
3.三角形的一个外角等于两个内角的和.(
)
练一练
1.图D-6-1中是△ABC的外角的是( )
A.∠EAB和∠EAD
B.∠EAB和∠DAC
C.∠EAB和∠EAD,∠DAC
D.以上说法都不对
B
图D-6-1
2.如图D-6-2,∠ACD是△ABC的外角,CE平分∠ACD,
若∠A=60°,∠B=40°,则∠ECD等于( )
A.40°
B.45°
C.50°
D.55°
C
随堂演练
图D-6-2
3
.如图,D是△ABC的BC边上一点,∠B=∠BAD,
∠ADC=80°,∠BAC=70°,求:(1)∠B
的度数;(2)∠C的度数.
C
D
解:因为∠ADC是△ABD的外角.
在△ABC中,
因为∠B+∠BAC+∠C=180°,
所以∠C=180?-∠B-∠BAC
=180?-40?-70?=70°.
所以∠ADC=∠B+∠BAD=80°.
又因为∠B=∠BAD,
B
A
课堂小结
三角形的外角
定义
角一边必须是三角形的一边,另一边必须是三角形另一边的延长线
性质
三角形的一个外角等于与它不相邻的两个内角的和
三角形的外角和
三角形的外角和等于360
°
https://www.21cnjy.com/help/help_extract.php
