12.2 三角形全等的判定(三)(“ASA”和“AAS”) 第3课时 (共20张PPT)
文档属性
| 名称 | 12.2 三角形全等的判定(三)(“ASA”和“AAS”) 第3课时 (共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-07 17:22:45 | ||
图片预览




文档简介
(共20张PPT)
第十二章
全等三角形
12.2 三角形全等的判定
随堂演练
获取新知
知识回顾
例题讲解
课堂小结
第3课时
三角形全等的判定(三)ASA、AAS
知识回顾
1.
什么是全等三角形?
2.
我们已经学过了哪几种判定两个三角形全等的方法?
能够完全重合的两个三角形叫做全等三角形.
边边边(SSS)和边角边(SAS).
获取新知
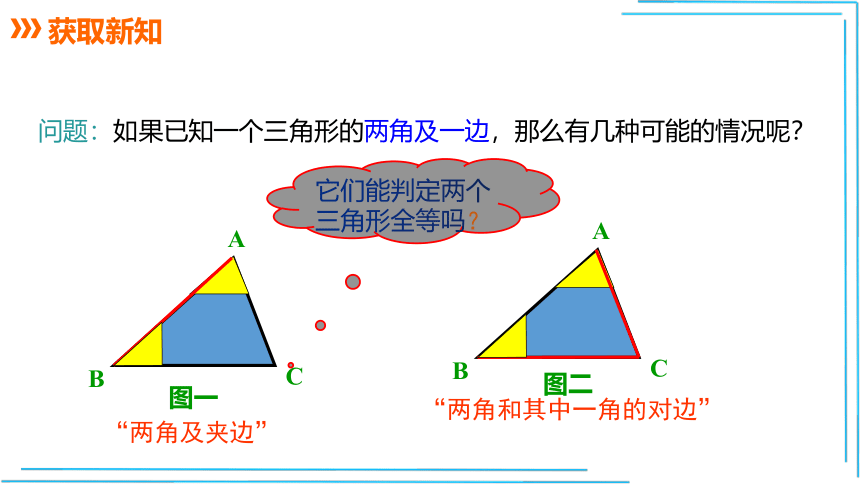
问题:如果已知一个三角形的两角及一边,那么有几种可能的情况呢?
A
B
C
A
B
C
图一
图二
“两角及夹边”
“两角和其中一角的对边”
它们能判定两个三角形全等吗?
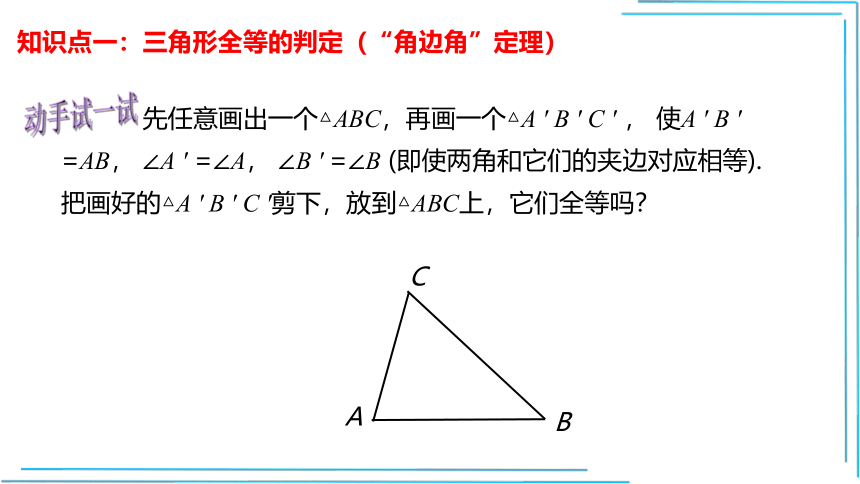
知识点一:三角形全等的判定(“角边角”定理)
先任意画出一个△ABC,再画一个△A
′
B
′
C
′
,
使A
′
B
′
=AB,
∠A
′
=∠A,
∠B
′
=∠B
(即使两角和它们的夹边对应相等).把画好的△A
′
B
′
C
′剪下,放到△ABC上,它们全等吗?
A
C
B
动手试一试
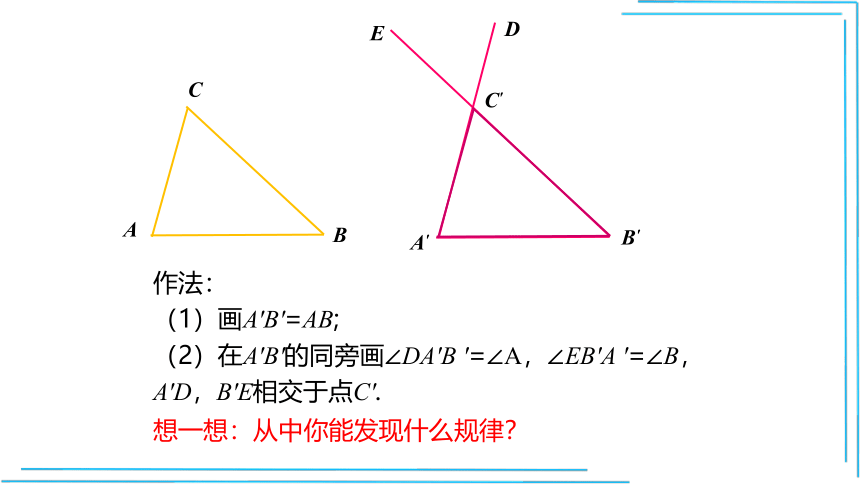
作法:
(1)画A'B'=AB;
(2)在A'B'的同旁画∠DA'B
'=∠A,∠EB'A
'=∠B,A'D,B'E相交于点C'.
想一想:从中你能发现什么规律?
A
C
B
A′
B′
C′
E
D
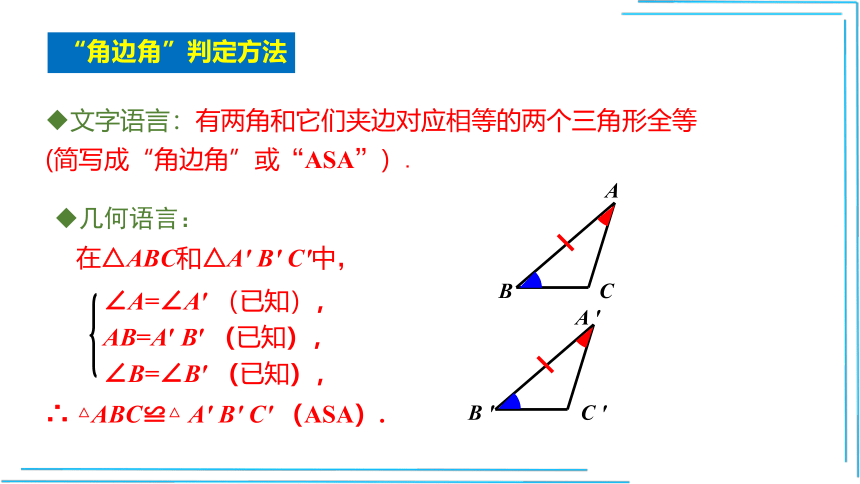
“角边角”判定方法
文字语言:有两角和它们夹边对应相等的两个三角形全等(简写成“角边角”或“ASA”).
几何语言:
∠A=∠A′
(已知),
AB=A′
B′
(已知),
∠B=∠B′
(已知),
在△ABC和△A′
B′
C′中,
∴
△ABC≌△
A′
B′
C′
(ASA).
A
B
C
A
′
B
′
C
′
例1
已知:如图,点D在AB上,点E在AC上
,AB=AC,∠B=∠C,
求证:AD=AE.
例题讲解
分析:证明△ACD≌△ABE,就可以得出AD=AE.
证明:在△ACD和△ABE中,
∠A=∠A(公共角
),
AC=AB(已知),
∠C=∠B
(已知
),
∴
△ACD≌△ABE(ASA),
∴AD=AE.
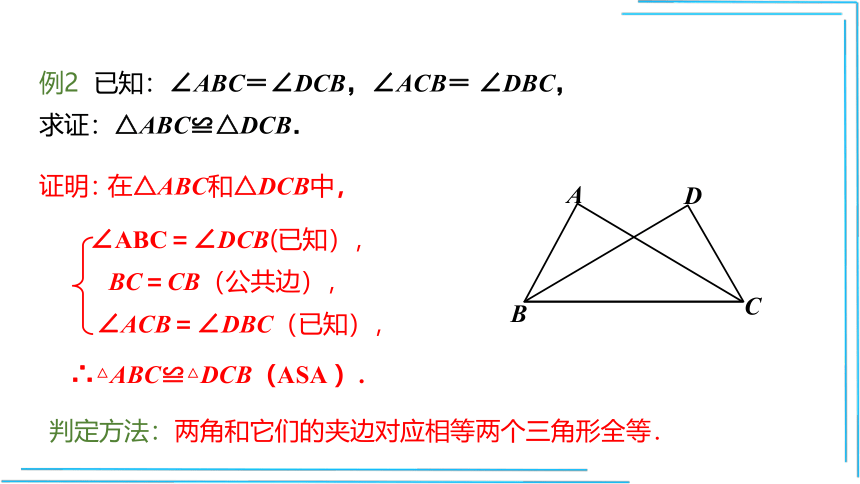
例2
已知:∠ABC=∠DCB,∠ACB=
∠DBC,
求证:△ABC≌△DCB.
∠ABC=∠DCB(已知),
BC=CB(公共边),
∠ACB=∠DBC(已知),
证明:
在△ABC和△DCB中,
∴△ABC≌△DCB(ASA
).
B
C
A
D
判定方法:两角和它们的夹边对应相等两个三角形全等.
知识点二:用“角角边”判定三角形全等
问题:若三角形的两个内角分别是60°和45°,且45°所对的边为3cm,你能画出这个三角形吗?
60°
45°
60°
45°
思考:
这里的条件与1中的条件有什么相同点与不同点?你能将它转化为1中的条件吗?
75°
两角和其中一角的对边对应相等的两个三角形全等.
简写成“角角边”或“AAS”.
几何语言:∵在△ABC和△
A'B'C'中
∠A=
∠A'
BC=
B'C'
∠B=
∠B'
{
∴
△ABC≌△
A'B'C'
(AAS)
A
C
B
A′
C′
B′
“角角边”判定方法
例3:在△ABC和△DEF中,∠A=∠D,∠B=
∠E,BC=EF.
求证:△ABC≌△DEF.
∠B=∠E,
BC=EF,
∠C=∠F.
证明:
在△ABC中,∠A+∠B+∠C=180°.
∴△ABC≌△DEF(ASA
).
∴
∠C=180°-∠A-∠B.
同理
∠F=180°-∠D-∠E.
又
∠A=∠D,∠B=
∠E,
∴
∠C=∠F.
在△ABC和△DEF中,
例题讲解
在证两三角形全等所需要的角相等时,目前通常采
用的方法有:(1)公共角、对顶角分别相等;(2)等角加(减)
等角,其和(差)相等,即等式的性质;(3)同角或等角的
余(补)角相等;(4)角平分线得到相等角;(5)平行线的同
位角、内错角相等;(6)直角都相等;(7)全等三角形对应
角相等;(8)第三角代换,即等量代换等.
归纳总结
随堂演练
1.如图D-12-4,已知∠1=∠2,BE=CD,根据“________”可知△ABE≌△ACD;若AB=5,AE=2,则CE=________.
图D-12-4
AAS
3
2.如图D-12-2所示,已知△ABC的六个元素,图D-12-3中的甲、乙、丙三个三角形中也标出了某些元素,则与△ABC全等的三角形是( )
A.只有乙
B.只有丙
C.甲和乙
D.乙和丙
图D-12-2
图D-12-3
D
A
C
D
B
1
2
证明:
∵
AB⊥BC,AD⊥DC,
∴
∠
B=∠D=90
°.
在△ABC和△ADC中,
∠1=∠2
(已知),
∠
B=∠D(已证),
AC=AC
(公共边),
∴
△ABC≌△ADC(AAS),
∴AB=AD.
3.已知:如图,
AB⊥BC,AD⊥DC,∠1=∠2,
求证:AB=AD.
课堂小结
角边角
角角边
内容
有两角及夹边对应相等的两个三角形全等(简写成
“ASA”)
应用
为证明线段和角相等提供了新的证法
注意
注意“角角边”、“角边角”中两角与边的区别
两角和其中一角的对边对应相等的两个三角形全等.(简写成“AAS”)
https://www.21cnjy.com/help/help_extract.php
第十二章
全等三角形
12.2 三角形全等的判定
随堂演练
获取新知
知识回顾
例题讲解
课堂小结
第3课时
三角形全等的判定(三)ASA、AAS
知识回顾
1.
什么是全等三角形?
2.
我们已经学过了哪几种判定两个三角形全等的方法?
能够完全重合的两个三角形叫做全等三角形.
边边边(SSS)和边角边(SAS).
获取新知
问题:如果已知一个三角形的两角及一边,那么有几种可能的情况呢?
A
B
C
A
B
C
图一
图二
“两角及夹边”
“两角和其中一角的对边”
它们能判定两个三角形全等吗?
知识点一:三角形全等的判定(“角边角”定理)
先任意画出一个△ABC,再画一个△A
′
B
′
C
′
,
使A
′
B
′
=AB,
∠A
′
=∠A,
∠B
′
=∠B
(即使两角和它们的夹边对应相等).把画好的△A
′
B
′
C
′剪下,放到△ABC上,它们全等吗?
A
C
B
动手试一试
作法:
(1)画A'B'=AB;
(2)在A'B'的同旁画∠DA'B
'=∠A,∠EB'A
'=∠B,A'D,B'E相交于点C'.
想一想:从中你能发现什么规律?
A
C
B
A′
B′
C′
E
D
“角边角”判定方法
文字语言:有两角和它们夹边对应相等的两个三角形全等(简写成“角边角”或“ASA”).
几何语言:
∠A=∠A′
(已知),
AB=A′
B′
(已知),
∠B=∠B′
(已知),
在△ABC和△A′
B′
C′中,
∴
△ABC≌△
A′
B′
C′
(ASA).
A
B
C
A
′
B
′
C
′
例1
已知:如图,点D在AB上,点E在AC上
,AB=AC,∠B=∠C,
求证:AD=AE.
例题讲解
分析:证明△ACD≌△ABE,就可以得出AD=AE.
证明:在△ACD和△ABE中,
∠A=∠A(公共角
),
AC=AB(已知),
∠C=∠B
(已知
),
∴
△ACD≌△ABE(ASA),
∴AD=AE.
例2
已知:∠ABC=∠DCB,∠ACB=
∠DBC,
求证:△ABC≌△DCB.
∠ABC=∠DCB(已知),
BC=CB(公共边),
∠ACB=∠DBC(已知),
证明:
在△ABC和△DCB中,
∴△ABC≌△DCB(ASA
).
B
C
A
D
判定方法:两角和它们的夹边对应相等两个三角形全等.
知识点二:用“角角边”判定三角形全等
问题:若三角形的两个内角分别是60°和45°,且45°所对的边为3cm,你能画出这个三角形吗?
60°
45°
60°
45°
思考:
这里的条件与1中的条件有什么相同点与不同点?你能将它转化为1中的条件吗?
75°
两角和其中一角的对边对应相等的两个三角形全等.
简写成“角角边”或“AAS”.
几何语言:∵在△ABC和△
A'B'C'中
∠A=
∠A'
BC=
B'C'
∠B=
∠B'
{
∴
△ABC≌△
A'B'C'
(AAS)
A
C
B
A′
C′
B′
“角角边”判定方法
例3:在△ABC和△DEF中,∠A=∠D,∠B=
∠E,BC=EF.
求证:△ABC≌△DEF.
∠B=∠E,
BC=EF,
∠C=∠F.
证明:
在△ABC中,∠A+∠B+∠C=180°.
∴△ABC≌△DEF(ASA
).
∴
∠C=180°-∠A-∠B.
同理
∠F=180°-∠D-∠E.
又
∠A=∠D,∠B=
∠E,
∴
∠C=∠F.
在△ABC和△DEF中,
例题讲解
在证两三角形全等所需要的角相等时,目前通常采
用的方法有:(1)公共角、对顶角分别相等;(2)等角加(减)
等角,其和(差)相等,即等式的性质;(3)同角或等角的
余(补)角相等;(4)角平分线得到相等角;(5)平行线的同
位角、内错角相等;(6)直角都相等;(7)全等三角形对应
角相等;(8)第三角代换,即等量代换等.
归纳总结
随堂演练
1.如图D-12-4,已知∠1=∠2,BE=CD,根据“________”可知△ABE≌△ACD;若AB=5,AE=2,则CE=________.
图D-12-4
AAS
3
2.如图D-12-2所示,已知△ABC的六个元素,图D-12-3中的甲、乙、丙三个三角形中也标出了某些元素,则与△ABC全等的三角形是( )
A.只有乙
B.只有丙
C.甲和乙
D.乙和丙
图D-12-2
图D-12-3
D
A
C
D
B
1
2
证明:
∵
AB⊥BC,AD⊥DC,
∴
∠
B=∠D=90
°.
在△ABC和△ADC中,
∠1=∠2
(已知),
∠
B=∠D(已证),
AC=AC
(公共边),
∴
△ABC≌△ADC(AAS),
∴AB=AD.
3.已知:如图,
AB⊥BC,AD⊥DC,∠1=∠2,
求证:AB=AD.
课堂小结
角边角
角角边
内容
有两角及夹边对应相等的两个三角形全等(简写成
“ASA”)
应用
为证明线段和角相等提供了新的证法
注意
注意“角角边”、“角边角”中两角与边的区别
两角和其中一角的对边对应相等的两个三角形全等.(简写成“AAS”)
https://www.21cnjy.com/help/help_extract.php
