12.2三角形全等的判定课堂同步习题 2021-2022学年八年级数学人教版上册(Word版 含答案)
文档属性
| 名称 | 12.2三角形全等的判定课堂同步习题 2021-2022学年八年级数学人教版上册(Word版 含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 409.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-07 09:12:56 | ||
图片预览

文档简介
2021-2022学年初中数学八年级上册课堂同步(人教版)
12.2三角形全等的判定(一)
时间:60分钟;
一、单选题
1.我国的纸伞工艺十分巧妙.如图,伞不论张开还是缩拢,伞柄始终平分同一平面内两条伞骨所成的角,从而保证伞圈能沿着伞柄滑动.为了证明这个结论,我们的依据是(
)
A.
B.
C.
D.
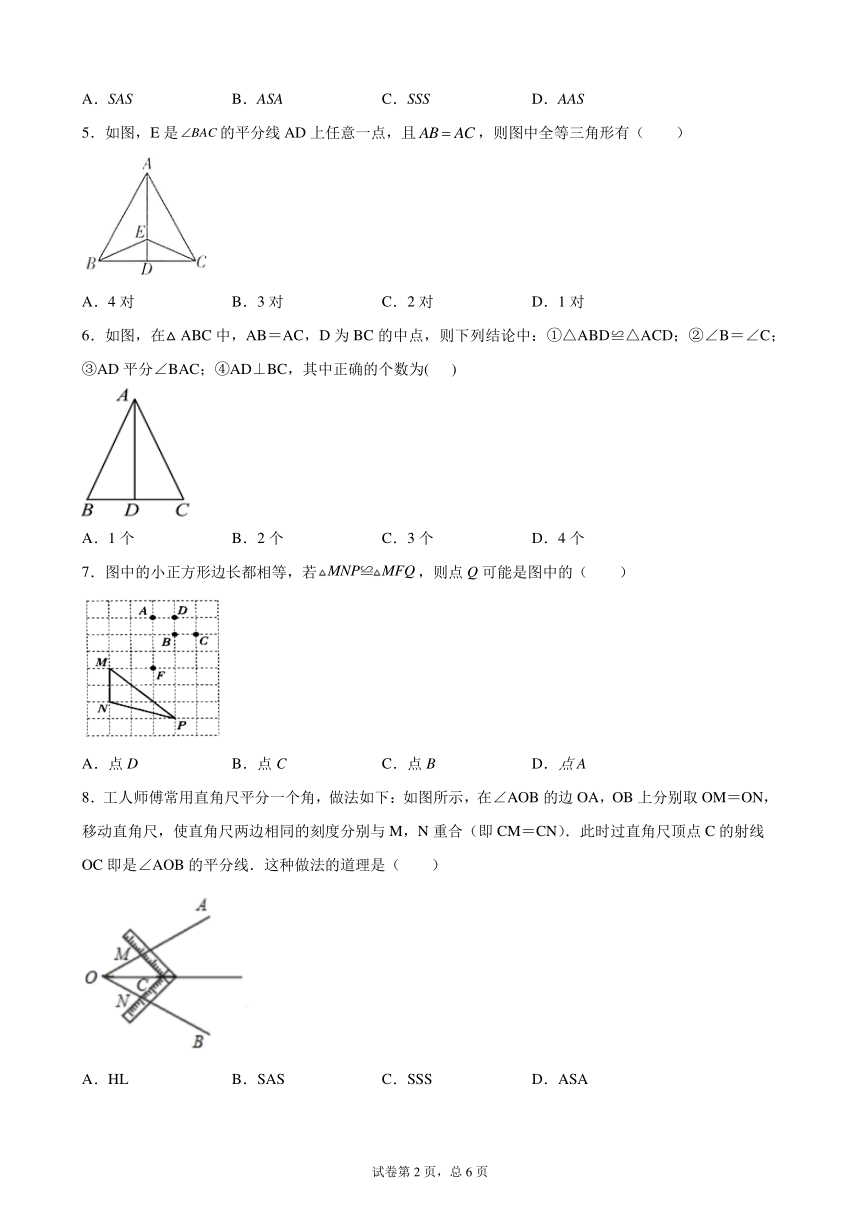
2.如图,△ABC中,AB=AC,BE=EC,直接使用“SSS”可判定( )
A.△ABD≌△ACD
B.△ABE≌△EDC
C.△ABE≌△ACE
D.△BED≌△CED
3.如图,由∠1=∠2,BC=DC,AC=EC,得△ABC≌△EDC的根据是(
)
A.SAS
B.ASA
C.AAS
D.SSS
4.如图,将两根钢条AA′、BB′的中点O连在一起,使AA′、BB′能绕着点O自由转动,就做成了一个测量工具,由三角形全等可知A′B′的长等于内槽宽AB,那么判定△OAB≌△OA′B′的理由是( )
A.SAS
B.ASA
C.SSS
D.AAS
5.如图,E是的平分线AD上任意一点,且,则图中全等三角形有(
)
A.4对
B.3对
C.2对
D.1对
6.如图,在△ABC中,AB=AC,D为BC的中点,则下列结论中:①△ABD≌△ACD;②∠B=∠C;③AD平分∠BAC;④AD⊥BC,其中正确的个数为(
)
A.1个
B.2个
C.3个
D.4个
7.图中的小正方形边长都相等,若,则点Q可能是图中的(
)
A.点D
B.点C
C.点B
D.点A
8.工人师傅常用直角尺平分一个角,做法如下:如图所示,在∠AOB的边OA,OB上分别取OM=ON,移动直角尺,使直角尺两边相同的刻度分别与M,N重合(即CM=CN).此时过直角尺顶点C的射线OC即是∠AOB的平分线.这种做法的道理是(
)
A.HL
B.SAS
C.SSS
D.ASA
二、填空题
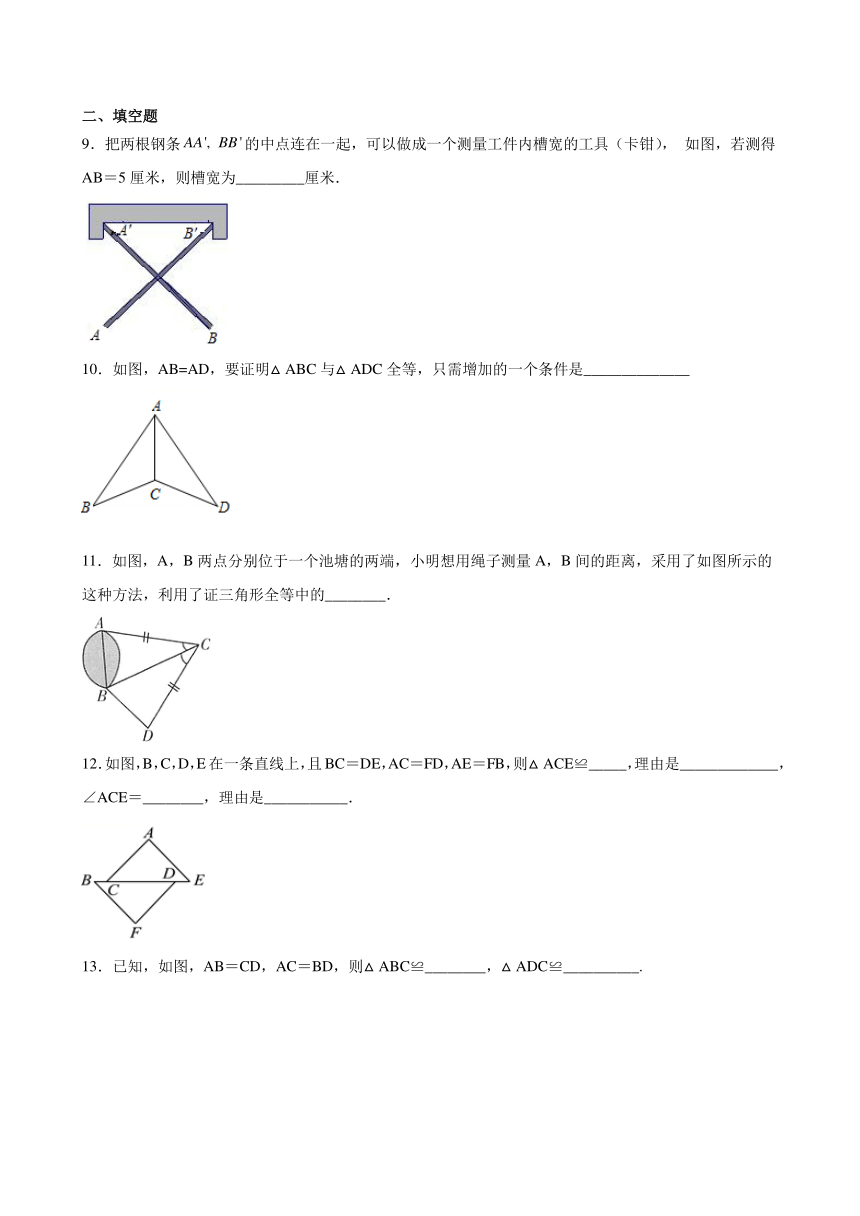
9.把两根钢条的中点连在一起,可以做成一个测量工件内槽宽的工具(卡钳),
如图,若测得AB=5厘米,则槽宽为_________厘米.
10.如图,AB=AD,要证明△ABC与△ADC全等,只需增加的一个条件是______________
11.如图,A,B两点分别位于一个池塘的两端,小明想用绳子测量A,B间的距离,采用了如图所示的这种方法,利用了证三角形全等中的________.
12.如图,B,C,D,E在一条直线上,且BC=DE,AC=FD,AE=FB,则△ACE≌_____,理由是_____________,∠ACE=________,理由是___________.
13.已知,如图,AB=CD,AC=BD,则△ABC≌________,△ADC≌__________.
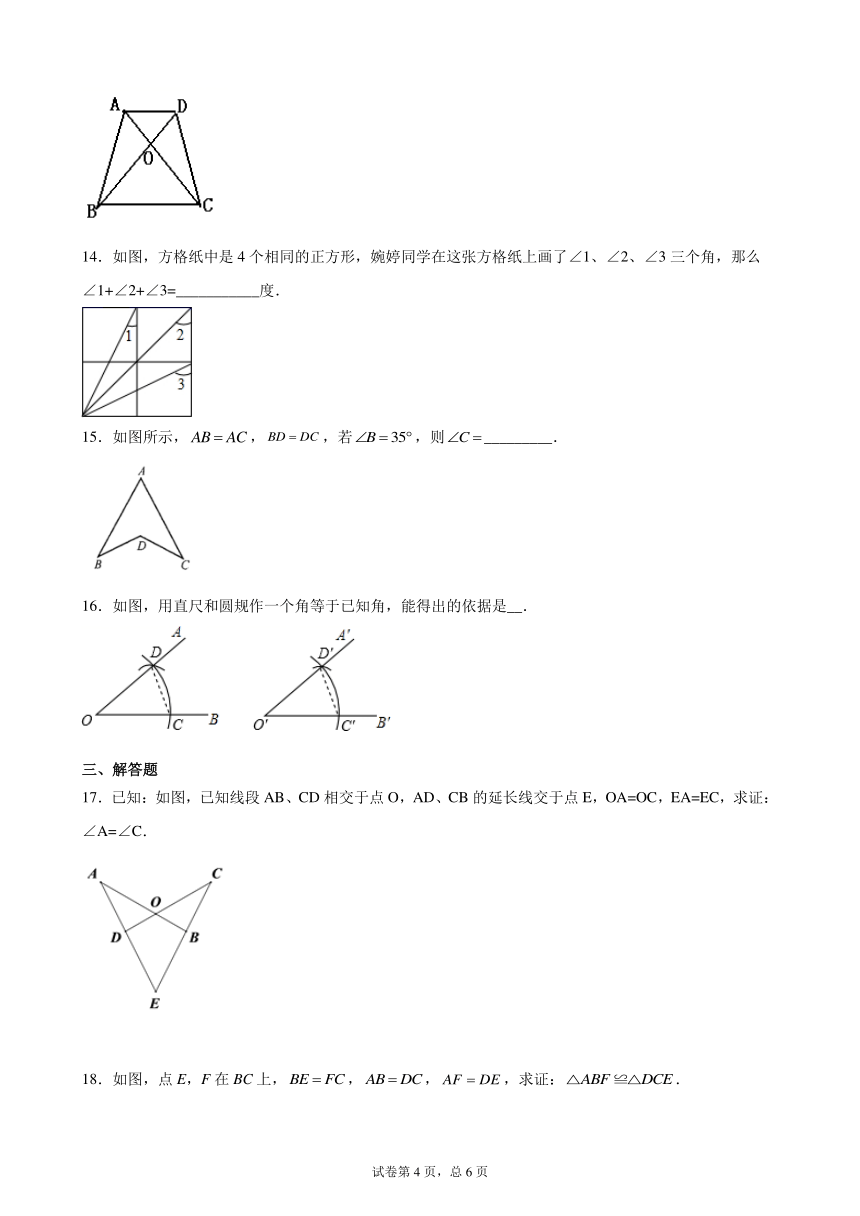
14.如图,方格纸中是4个相同的正方形,婉婷同学在这张方格纸上画了∠1、∠2、∠3三个角,那么∠1+∠2+∠3=___________度.
15.如图所示,,,若,则_________.
16.如图,用直尺和圆规作一个角等于已知角,能得出的依据是__.
三、解答题
17.已知:如图,已知线段AB、CD相交于点O,AD、CB的延长线交于点E,OA=OC,EA=EC,求证:∠A=∠C.
18.如图,点E,F在BC上,,,,求证:.
19..
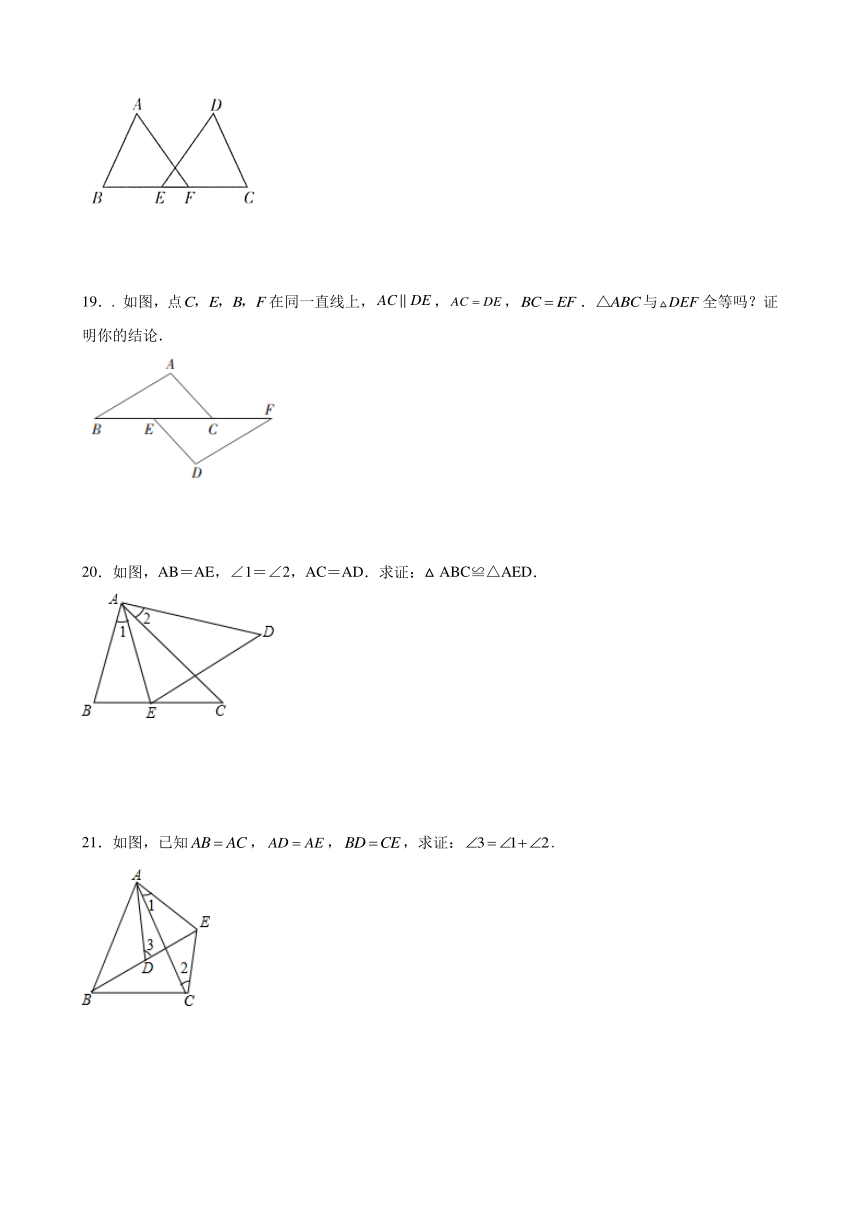
如图,点在同一直线上,,,.与全等吗?证明你的结论.
20.如图,AB=AE,∠1=∠2,AC=AD.求证:△ABC≌△AED.
21.如图,已知,,,求证:.
22.如图,已知:PA=PB,AC=BD,PC=PD,△PAD和△PBC全等吗?请说明理由.
23.为在池塘两侧的A,B两处架桥,要想测量A,B两点的距离,如图所示,找一处看得见A,B的点P,连接AP并延长到D,使PA=PD,连接BP并延长到C,使BP=CP.测得CD=35m,就确定了AB也是35m,说明其中的理由;
24.如图,点E在CD上,BC与AE交于点F,AB=CB,BE=BD,∠1=∠2.
(1)求证:;
(2)证明:∠1=∠3.
试卷第2页,总2页
参考答案
1.A
【解析】根据伞的结构,,伞骨,是公共边,
在和中,
,
,
,
即平分.
故选:.
2.C
【解析】解:△ABE≌△ACE,
理由是:在△ABE和△ACE中
∵
∴△ABE≌△ACE(SSS),
故选:C.
3.A
【解析】∵∠1=∠2,∴∠ACD+∠2=∠ACD+∠1,即∠ACB=∠ECD.又∵BC=DC,AC=EC,∴△ABC≌△EDC(SAS).故选A.
4.A
【解析】∵O是AA′、BB′的中点,
∴AO=A′O,BO=B′O,
在△OAB和△OA′B′中
,
∴△OAB≌△OA′B′(SAS),
故选:A.
5.B
【解析】∵AD平分∠BAC,
∴∠BAD=∠CAD,
在△ABD和△ACD中,
,
∴△ABD≌△ACD(SAS),
∴BD=CD,∠ADB=∠ADC,
在△BED和△CED中,
,
∴△BDE≌△CDE(SAS),
在△ABE和△ACE中,
,
∴△ABE≌△ACE(SAS),
共3对全等三角形,
故选:B.
6.D
【解析】∵D为BC的中点,
∴BD=CD,
又∵AB=AC,AD为公共边
∴△ABD≌△ACD(SSS),故①正确,
∴∠B=∠C,∠BAD=∠CAD,∠ADB=∠ADC,
∵∠ADB+∠ADC=180°,
∴∠ADB=∠ADC=90°,即AD⊥BC,故②③④正确.
综上所述:正确的结论有①②③④共4个,
故选D.
7.A
【解析】解:观察图象可知△MNP≌△MFD.
故选:A.
8.C
【解析】在△OMC和△ONC中,
,
∴△OMC≌△ONC(SSS),
∴∠MOC=∠NOC,
∴射线OC即是∠AOB的平分线,
故选:C.
9.5
【解析】解:连接,,设为和的中点,
,,
,
即,
故(厘米),
故答案为:5.
10.DC=BC(答案不唯一)
【解析】解:∵AB=AD,AC=AC
∴要使△ABC≌△ADC可利用SSS判定,
故添加DC=BC(答案不唯一).
故答案为:BC=DC,(答案不唯一).
11.SAS
【解析】观察图形发现:,,,
所以利用了证三角形全等中的SAS(或边角边).
故答案为:SAS.
12.△FDB
SSS
∠FDB
全等三角形的对应角相等
【解析】∵BC=DE,
∴BC+CD=DE+CD,即BD=CE,
又∵AC=FD,AE=FB,
∴△ACE≌△FDB,(SSS)
∵全等三角形对应角相等,
∴∠ACE=∠FDB,
故答案为△FDB;SSS;∠FDB;全等三角形的对应角相等
13.△DCB,
△DAB.
【解析】∵AB=CD,AC=BD,BC=CB,
∴△ABC≌△DCB(SSS),
∵AB=CD,AC=BD,AD=AD,
∴△ADC≌△DAB.
14.135
【解析】由题意可知△ABC≌△EDC,
∴∠3=∠BAC,
又∵∠1+∠BAC=90°,
∴∠1+∠3=90°,
∵DF=DC,
∴∠2=45°,
∴∠1+∠2+∠3=135度,
故答案为135.
15.
【解析】如图所示:连接AD,
在△ABD和△ACD中,
,
∴△ABD≌△ACD(SSS),
∴,
又∵,
∴.
故答案为:.
16.
【解析】在和△中,
,
△,
故答案为:.
17.证明见解析
【解析】如图,连结OE
在△OEA和△OEC中
∴△OEA≌△OEC(SSS)
∴∠A=∠C(全等三角形的对应角相等)
18.详见解析
【解析】,
,即,
在与中,
,
.
19.全等
【解析】解:与全等
∴∠ACB=∠DEF,
在与中
20.见解析.
【解析】∵∠1=∠2,∴∠BAC=∠EAD.
在△ABC和△AED中,∵,∴△ABC≌△AED(SAS).
21.证明见解析.
【解析】在△ABD和△ACE中,,
∴△ABD≌△ACE,
∴∠BAD=∠1,∠ABD=∠2,
∵∠3=∠BAD+∠ABD,
∴∠3=∠1+∠2.
22.详见解析
【解析】∵AC=BD,
∴AC+CD=BD+CD,即AD=BC,
又∵PA=PB,PC=PD,
∴△PAD≌△PBC(SSS)
23.35
m
【解析】∵PA=PD
PC=PB
又∠APB=∠CPD
∴△APB≌△DPC,
∴AB=CD=35
m.
24.(1)证明见解析;(2)证明见解析.
【解析】(1),
,即,
在和中,,
;
(2)由(1)已证:,
,
由对顶角相等得:,
又,
.
答案第1页,总2页
答案第1页,总2页
12.2三角形全等的判定(一)
时间:60分钟;
一、单选题
1.我国的纸伞工艺十分巧妙.如图,伞不论张开还是缩拢,伞柄始终平分同一平面内两条伞骨所成的角,从而保证伞圈能沿着伞柄滑动.为了证明这个结论,我们的依据是(
)
A.
B.
C.
D.
2.如图,△ABC中,AB=AC,BE=EC,直接使用“SSS”可判定( )
A.△ABD≌△ACD
B.△ABE≌△EDC
C.△ABE≌△ACE
D.△BED≌△CED
3.如图,由∠1=∠2,BC=DC,AC=EC,得△ABC≌△EDC的根据是(
)
A.SAS
B.ASA
C.AAS
D.SSS
4.如图,将两根钢条AA′、BB′的中点O连在一起,使AA′、BB′能绕着点O自由转动,就做成了一个测量工具,由三角形全等可知A′B′的长等于内槽宽AB,那么判定△OAB≌△OA′B′的理由是( )
A.SAS
B.ASA
C.SSS
D.AAS
5.如图,E是的平分线AD上任意一点,且,则图中全等三角形有(
)
A.4对
B.3对
C.2对
D.1对
6.如图,在△ABC中,AB=AC,D为BC的中点,则下列结论中:①△ABD≌△ACD;②∠B=∠C;③AD平分∠BAC;④AD⊥BC,其中正确的个数为(
)
A.1个
B.2个
C.3个
D.4个
7.图中的小正方形边长都相等,若,则点Q可能是图中的(
)
A.点D
B.点C
C.点B
D.点A
8.工人师傅常用直角尺平分一个角,做法如下:如图所示,在∠AOB的边OA,OB上分别取OM=ON,移动直角尺,使直角尺两边相同的刻度分别与M,N重合(即CM=CN).此时过直角尺顶点C的射线OC即是∠AOB的平分线.这种做法的道理是(
)
A.HL
B.SAS
C.SSS
D.ASA
二、填空题
9.把两根钢条的中点连在一起,可以做成一个测量工件内槽宽的工具(卡钳),
如图,若测得AB=5厘米,则槽宽为_________厘米.
10.如图,AB=AD,要证明△ABC与△ADC全等,只需增加的一个条件是______________
11.如图,A,B两点分别位于一个池塘的两端,小明想用绳子测量A,B间的距离,采用了如图所示的这种方法,利用了证三角形全等中的________.
12.如图,B,C,D,E在一条直线上,且BC=DE,AC=FD,AE=FB,则△ACE≌_____,理由是_____________,∠ACE=________,理由是___________.
13.已知,如图,AB=CD,AC=BD,则△ABC≌________,△ADC≌__________.
14.如图,方格纸中是4个相同的正方形,婉婷同学在这张方格纸上画了∠1、∠2、∠3三个角,那么∠1+∠2+∠3=___________度.
15.如图所示,,,若,则_________.
16.如图,用直尺和圆规作一个角等于已知角,能得出的依据是__.
三、解答题
17.已知:如图,已知线段AB、CD相交于点O,AD、CB的延长线交于点E,OA=OC,EA=EC,求证:∠A=∠C.
18.如图,点E,F在BC上,,,,求证:.
19..
如图,点在同一直线上,,,.与全等吗?证明你的结论.
20.如图,AB=AE,∠1=∠2,AC=AD.求证:△ABC≌△AED.
21.如图,已知,,,求证:.
22.如图,已知:PA=PB,AC=BD,PC=PD,△PAD和△PBC全等吗?请说明理由.
23.为在池塘两侧的A,B两处架桥,要想测量A,B两点的距离,如图所示,找一处看得见A,B的点P,连接AP并延长到D,使PA=PD,连接BP并延长到C,使BP=CP.测得CD=35m,就确定了AB也是35m,说明其中的理由;
24.如图,点E在CD上,BC与AE交于点F,AB=CB,BE=BD,∠1=∠2.
(1)求证:;
(2)证明:∠1=∠3.
试卷第2页,总2页
参考答案
1.A
【解析】根据伞的结构,,伞骨,是公共边,
在和中,
,
,
,
即平分.
故选:.
2.C
【解析】解:△ABE≌△ACE,
理由是:在△ABE和△ACE中
∵
∴△ABE≌△ACE(SSS),
故选:C.
3.A
【解析】∵∠1=∠2,∴∠ACD+∠2=∠ACD+∠1,即∠ACB=∠ECD.又∵BC=DC,AC=EC,∴△ABC≌△EDC(SAS).故选A.
4.A
【解析】∵O是AA′、BB′的中点,
∴AO=A′O,BO=B′O,
在△OAB和△OA′B′中
,
∴△OAB≌△OA′B′(SAS),
故选:A.
5.B
【解析】∵AD平分∠BAC,
∴∠BAD=∠CAD,
在△ABD和△ACD中,
,
∴△ABD≌△ACD(SAS),
∴BD=CD,∠ADB=∠ADC,
在△BED和△CED中,
,
∴△BDE≌△CDE(SAS),
在△ABE和△ACE中,
,
∴△ABE≌△ACE(SAS),
共3对全等三角形,
故选:B.
6.D
【解析】∵D为BC的中点,
∴BD=CD,
又∵AB=AC,AD为公共边
∴△ABD≌△ACD(SSS),故①正确,
∴∠B=∠C,∠BAD=∠CAD,∠ADB=∠ADC,
∵∠ADB+∠ADC=180°,
∴∠ADB=∠ADC=90°,即AD⊥BC,故②③④正确.
综上所述:正确的结论有①②③④共4个,
故选D.
7.A
【解析】解:观察图象可知△MNP≌△MFD.
故选:A.
8.C
【解析】在△OMC和△ONC中,
,
∴△OMC≌△ONC(SSS),
∴∠MOC=∠NOC,
∴射线OC即是∠AOB的平分线,
故选:C.
9.5
【解析】解:连接,,设为和的中点,
,,
,
即,
故(厘米),
故答案为:5.
10.DC=BC(答案不唯一)
【解析】解:∵AB=AD,AC=AC
∴要使△ABC≌△ADC可利用SSS判定,
故添加DC=BC(答案不唯一).
故答案为:BC=DC,(答案不唯一).
11.SAS
【解析】观察图形发现:,,,
所以利用了证三角形全等中的SAS(或边角边).
故答案为:SAS.
12.△FDB
SSS
∠FDB
全等三角形的对应角相等
【解析】∵BC=DE,
∴BC+CD=DE+CD,即BD=CE,
又∵AC=FD,AE=FB,
∴△ACE≌△FDB,(SSS)
∵全等三角形对应角相等,
∴∠ACE=∠FDB,
故答案为△FDB;SSS;∠FDB;全等三角形的对应角相等
13.△DCB,
△DAB.
【解析】∵AB=CD,AC=BD,BC=CB,
∴△ABC≌△DCB(SSS),
∵AB=CD,AC=BD,AD=AD,
∴△ADC≌△DAB.
14.135
【解析】由题意可知△ABC≌△EDC,
∴∠3=∠BAC,
又∵∠1+∠BAC=90°,
∴∠1+∠3=90°,
∵DF=DC,
∴∠2=45°,
∴∠1+∠2+∠3=135度,
故答案为135.
15.
【解析】如图所示:连接AD,
在△ABD和△ACD中,
,
∴△ABD≌△ACD(SSS),
∴,
又∵,
∴.
故答案为:.
16.
【解析】在和△中,
,
△,
故答案为:.
17.证明见解析
【解析】如图,连结OE
在△OEA和△OEC中
∴△OEA≌△OEC(SSS)
∴∠A=∠C(全等三角形的对应角相等)
18.详见解析
【解析】,
,即,
在与中,
,
.
19.全等
【解析】解:与全等
∴∠ACB=∠DEF,
在与中
20.见解析.
【解析】∵∠1=∠2,∴∠BAC=∠EAD.
在△ABC和△AED中,∵,∴△ABC≌△AED(SAS).
21.证明见解析.
【解析】在△ABD和△ACE中,,
∴△ABD≌△ACE,
∴∠BAD=∠1,∠ABD=∠2,
∵∠3=∠BAD+∠ABD,
∴∠3=∠1+∠2.
22.详见解析
【解析】∵AC=BD,
∴AC+CD=BD+CD,即AD=BC,
又∵PA=PB,PC=PD,
∴△PAD≌△PBC(SSS)
23.35
m
【解析】∵PA=PD
PC=PB
又∠APB=∠CPD
∴△APB≌△DPC,
∴AB=CD=35
m.
24.(1)证明见解析;(2)证明见解析.
【解析】(1),
,即,
在和中,,
;
(2)由(1)已证:,
,
由对顶角相等得:,
又,
.
答案第1页,总2页
答案第1页,总2页
