22.3二次函数实际问题 强化练习卷 2021-2022学年人教版数学九年级上册同步专题六(Word版 含答案)
文档属性
| 名称 | 22.3二次函数实际问题 强化练习卷 2021-2022学年人教版数学九年级上册同步专题六(Word版 含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 170.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-07 09:20:43 | ||
图片预览



文档简介
人教版数学九年级上册同步专题六
《二次函数实际问题》强化练习卷
一、选择题
1.某商品现在的售价为每件60元,每星期可卖出300件.市场调查反映,如果调整商品售价,每降价1元,每星期可多卖出20件.设每件商品降价x元后,每星期售出商品的总销售额为y元,则y与x的关系式为(
)
A.y=60
B.y=(60﹣x)
C.y=300(60﹣20x)
D.y=(60﹣x)
2.烟花厂为热烈庆祝“十一国庆”,特别设计制作一种新型礼炮,这种礼炮的升空高度h(m)与飞行时间t(s)的关系式是h=-2.5t2+30t+1,礼炮点火升空后会在最高点处引爆,则这种礼炮能上升的最大高度为(
)
A.91米
B.90米
C.81米
D.80米
3.如图,某校的围墙由一段相同的凹曲拱组成,其拱状图形为抛物线的一部分,栅栏的跨径AB以相同间隔0.2米用5根立柱加固,拱高OC为0.36米,则立柱EF的长为(
)
A.0.4米
B.0.16米
C.0.2米
D.0.24米
4.向空中发射一枚炮弹,经x秒后的高度为y米,且时间与高度的关系为y=ax2+bx+c(a≠0).若此炮弹在第7秒与第14秒时的高度相等,则在下列时间中炮弹所在高度最高的是(
)
A.第8秒
B.第10秒
C.第12秒
D.第15秒
5.如图所示,向一个半径为R、容积为V的球形容器内注水,则能够反映容器内水的体积y与容器内水深x间的函数关系的图象可能是(
)
A.
B.
C.
D.
6.某商家销售某种商品,当单价为10元时,每天能卖出200个.现在采用提高售价方法来增加利润,已知商品单价每上涨1元,每天销售量就少10个,则每天销售金额最大为(
)
A.2500元
B.2250元
C.2160元
D.2000元
7.如图所示,△ABC是直角三角形,∠A=90°,AB=8cm,AC=6cm.点P从点A出发,沿AB方向以2cm/s的速度向点B运动,同时点Q从点A出发,沿AC方向以1cm/s的速度向点C运动,其中一个动点到达终点时另一个动点也停止运动,则△APQ的最大面积是(
).
A.10cm2
B.8cm2
C.16cm2
D.24cm2
8.足球运动员将足球沿与地面成一定角度的方向踢出,足球飞行的路线是一条抛物线,不考虑空气阻力,足球距离地面的高度h(单位:m)与足球被踢出后经过的时间t(单位:s)之间的关系如下表所示:
下列结论:
①足球距离地面的最大高度为20m;
②足球飞行路线的对称轴是直线t=4.5;
③足球被踢出9s时落地;
④足球被踢出1.5s时,距离地面的高度是11m.
其中结论正确的个数是(
).
A.1
B.2
C.3
D.4
二、填空题
9.小峰家要在一面长为38m的墙的一侧修建4个同样大小的猪圈,并在如图所示的5处各留1.5m宽的门,已知现有的材料共可修建长为41m的墙体,则能修建的4个猪圈的最大面积为
.
10.如图,线段AB的长为5,C为线段AB上一动点(与点A、B不重合),分别以AC、BC为斜边在AB的同侧作等腰直角三角形ACD和BCE,若AD=x,BE=y,那么x2+y2最小值是______.
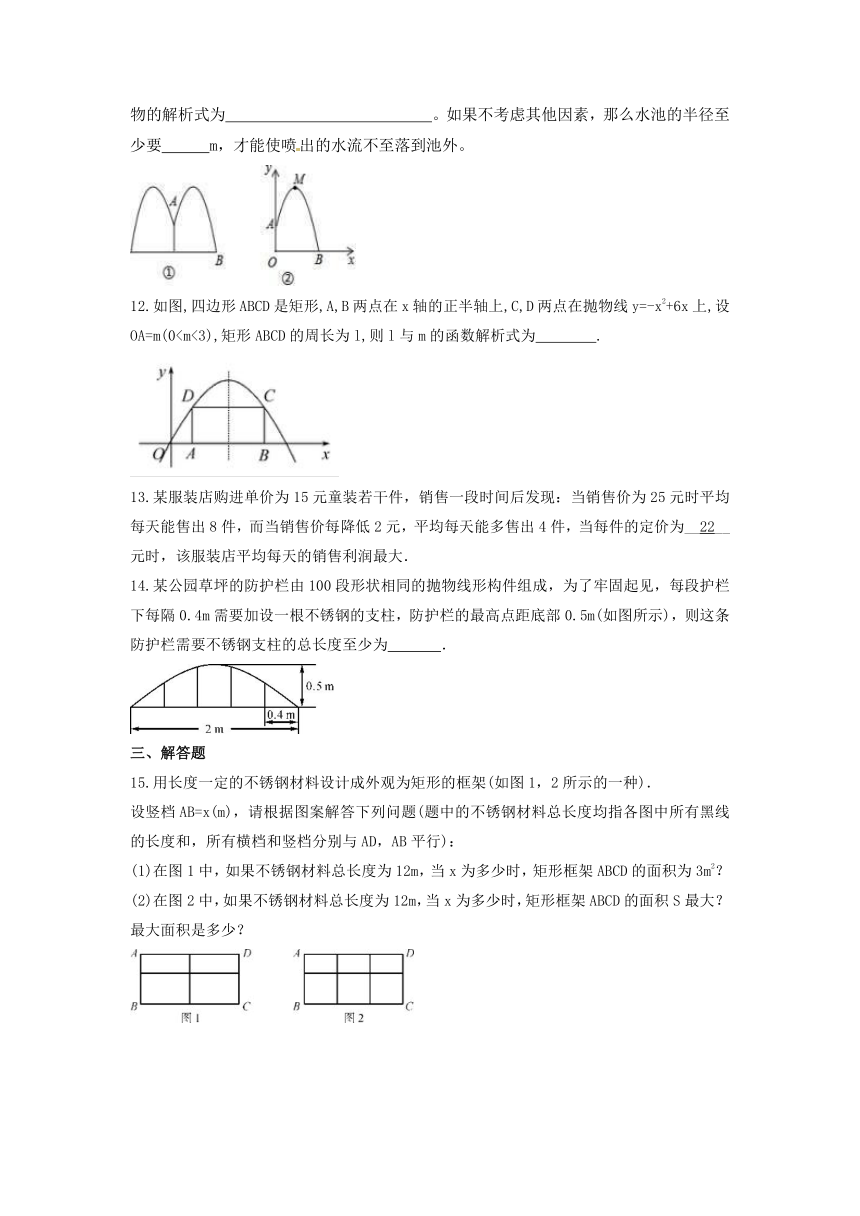
11.如图是某公园一圆形喷水池,水流在各个方向沿形状相同的抛物线落下,建立如下图所示的坐标系,如果喷头所在处A(0,1.25),水流路线最高处M(1,2.25),则该抛物的解析式为
。如果不考虑其他因素,那么水池的半径至少要
m,才能使喷出的水流不至落到池外。
12.如图,四边形ABCD是矩形,A,B两点在x轴的正半轴上,C,D两点在抛物线y=-x2+6x上,设OA=m(0.
13.某服装店购进单价为15元童装若干件,销售一段时间后发现:当销售价为25元时平均每天能售出8件,而当销售价每降低2元,平均每天能多售出4件,当每件的定价为__22__元时,该服装店平均每天的销售利润最大.
14.某公园草坪的防护栏由100段形状相同的抛物线形构件组成,为了牢固起见,每段护栏下每隔0.4m需要加设一根不锈钢的支柱,防护栏的最高点距底部0.5m(如图所示),则这条防护栏需要不锈钢支柱的总长度至少为
.
三、解答题
15.用长度一定的不锈钢材料设计成外观为矩形的框架(如图1,2所示的一种).
设竖档AB=x(m),请根据图案解答下列问题(题中的不锈钢材料总长度均指各图中所有黑线的长度和,所有横档和竖档分别与AD,AB平行):
(1)在图1中,如果不锈钢材料总长度为12m,当x为多少时,矩形框架ABCD的面积为3m2?
(2)在图2中,如果不锈钢材料总长度为12m,当x为多少时,矩形框架ABCD的面积S最大?最大面积是多少?
16.端午节前夕,三位同学到某超市调研一种进价为80元的粽子礼盒的销售情况,请根据小梅提供的信息,解答小慧和小杰提出的问题.(价格取正整数)
小梅:每盒定价100元,每天能卖出410盒,而且这种粽子礼盒的售价每上涨1元,其销售量减少10盒.
小慧:照你所说,如果要实现每天8580元的销售利润,并且薄利多销,那么该如何定价?小杰:8580元的销售利润是不是最大呢?如果不是,又该怎样定价才会使每天的销售利润最大?每天的最大销售利润是多少?
17.市场需求,某市电子玩具制造公司技术部研制开发一种新产品,年初上市后,公司经历了从亏损到盈利的过程.如图所示的二次函数图象(部分)刻画了该公司年初以来累积利润s(万元)与销售时间t(月)之间的关系(即前t个月的利润总和s和t之间的关系).根据图象提供的信息,解答下列问题:
(1)根据图象,求累积利润s(万元)关于时间t(月)的二次函数的表达式.
(2)截止到几月末,公司累积利润可达到6万元?
(3)第9个月公司所获利润是多少万元?
18.某超市销售一种商品,成本每千克40元,规定每千克售价不低于成本,且不高于80元.经市场调查,每天的销售量y(千克)与每千克售价x(元)满足一次函数关系,部分数据如下表所示:
(1)求y关于x的函数表达式.
(2)设商品每天的总利润为W(元),求W关于x的函数表达式(利润=收入-成本).
(3)试说明(2)中总利润W随售价x的变化而变化的情况,并指出售价为多少元时获得最大利润,最大利润是多少.
19.甲、乙两人进行羽毛球比赛,羽毛球飞行的路线为抛物线的一部分,如图所示,甲在O点正上方1m的P处发出一球,羽毛球飞行的高度y(m)与水平距离x(m)之间满足函数表达式y=a(x-4)2+h,已知点O与球网的水平距离为5m,球网的高度为1.55m.
(1)当a=-时,①求h的值.②通过计算判断此球能否过网.
(2)若甲发球过网后,羽毛球飞行到与点O的水平距离为7m,离地面的高度为m的Q处时,乙扣球成功,求a的值.
20.某商店销售一种商品,童威经市场调查发现:该商品的周销售量y(件)是售价x(元/件)的一次函数,其售价、周销售量、周销售利润w(元)的三组对应值如下表:
注:周销售利润=周销售量×(售价-进价)
(1)①求y关于x的函数解析式(不要求写出自变量的取值范围)
②该商品进价是_________元/件;当售价是________元/件时,周销售利润最大,最大利润是
__________元
(2)由于某种原因,该商品进价提高了m元/件(m>0),物价部门规定该商品售价不得超过65元/件,该商店在今后的销售中,周销售量与售价仍然满足(1)中的函数关系.若周销售最大利润是1400元,求m的值
参考答案
1.B
2.A
3.C
4.B
5.A
6.B.
7.C.
8.B.
9.答案为:9409/80.
10.答案为:.
11.答案为:y=-x2
+2x+1.25,
12.答案为:l=-2m2+8m+12
13.答案为:22
14.答案为:160.
15.解:(1)由题意得BC的长为(4-x)(m),
∴x(4-x)=3,
即x2-4x+3=0,解得x1=1,x2=3.
∴当x=1或3时,矩形框架ABCD的面积为3m2.
(2)由题意得AD=(12-4x)÷3=4-x,
∴S=x(4-x)=-
x2+4x=-(x-)2+3.
∴当x=时,矩形框架ABCD的面积最大,最大面积是3m2.
16.解:小慧:设定价为x元,利润为y元,
则销售量为410-10(x-100)=1410-10x,
由题意得y=(x-80)(1410-10x)=-10x2+2210x-112800,
当y=8580时,-10x2+2210x-112800=8580,
整理得x2-221x+12138=0,解得x=102或x=119.
∵当x=102时,销量为1410-1020=390,
当x=119时,销量为1410-1190=220,
∴若要达到8580元的利润,且薄利多销,此时的定价应为102元.
小杰:y=-10x2+2210x-112800=-10(x-)2+,
∵价格取整数,即x为整数,
∴当x=110或x=111时,y取得最大值,最大值为9300,
∴每天8580元的销售利润不是最大的,当定价为110元或111元时,每天的销售利润最大,最大销售利润为9300元.
17.解:(1)由图象可知抛物线顶点坐标为(2,-2),与x轴交点为(0,0),(4,0).
可设函数表达式为s=a(t-2)2-2.
将(0,0)代入得4a-2=0,解得a=.
∴s=(t-2)2-2.
(2)当累积利润达到6万元时,s=(t-2)2-2=6,解得t=6或-2(舍去).
∴截止到6月末公司累积利润可达到6万元.
(3)当t=9时,s=(t-2)2-2=(9-2)2-2=22.5(万元);
当t=8时,s=(t-2)2-2=(8-2)2-2=16(万元).
∵22.5-16=6.5(万元),
∴第9个月公司所获利润是6.5万元.
18.解:(1)设y关于x的函数表达式为y=kx+b.
由题意得,解得.
∴y关于x的函数表达式为y=-2x+200.
(2)W=(x-40)(-2x+200)=-2x2+280x-8000.
(3)∵W=-2x2+280x-8000=-2(x-70)2+1800,40≤x≤80,
∴当40≤x≤70时,W随x的增大而增大;
当70≤x≤80时,W随x的增大而减小;
当x=70时,W取得最大值,此时W=1800,
即售价为70元时获得最大利润,最大利润是1800元.
19.解:(1)①当a=-时,y=-
(x-4)2+h,
将点P(0,1)代入,得-×16+h=1,解得h=.
②把x=5代入y=-
(x-4)2+,得y=-×(5-4)2+=1.625,
∵1.625>1.55,
∴此球能过网.
(2)把(0,1),(7,)代入y=a(x-4)2+h,
得,解得.
∴a=-.
20.解:
《二次函数实际问题》强化练习卷
一、选择题
1.某商品现在的售价为每件60元,每星期可卖出300件.市场调查反映,如果调整商品售价,每降价1元,每星期可多卖出20件.设每件商品降价x元后,每星期售出商品的总销售额为y元,则y与x的关系式为(
)
A.y=60
B.y=(60﹣x)
C.y=300(60﹣20x)
D.y=(60﹣x)
2.烟花厂为热烈庆祝“十一国庆”,特别设计制作一种新型礼炮,这种礼炮的升空高度h(m)与飞行时间t(s)的关系式是h=-2.5t2+30t+1,礼炮点火升空后会在最高点处引爆,则这种礼炮能上升的最大高度为(
)
A.91米
B.90米
C.81米
D.80米
3.如图,某校的围墙由一段相同的凹曲拱组成,其拱状图形为抛物线的一部分,栅栏的跨径AB以相同间隔0.2米用5根立柱加固,拱高OC为0.36米,则立柱EF的长为(
)
A.0.4米
B.0.16米
C.0.2米
D.0.24米
4.向空中发射一枚炮弹,经x秒后的高度为y米,且时间与高度的关系为y=ax2+bx+c(a≠0).若此炮弹在第7秒与第14秒时的高度相等,则在下列时间中炮弹所在高度最高的是(
)
A.第8秒
B.第10秒
C.第12秒
D.第15秒
5.如图所示,向一个半径为R、容积为V的球形容器内注水,则能够反映容器内水的体积y与容器内水深x间的函数关系的图象可能是(
)
A.
B.
C.
D.
6.某商家销售某种商品,当单价为10元时,每天能卖出200个.现在采用提高售价方法来增加利润,已知商品单价每上涨1元,每天销售量就少10个,则每天销售金额最大为(
)
A.2500元
B.2250元
C.2160元
D.2000元
7.如图所示,△ABC是直角三角形,∠A=90°,AB=8cm,AC=6cm.点P从点A出发,沿AB方向以2cm/s的速度向点B运动,同时点Q从点A出发,沿AC方向以1cm/s的速度向点C运动,其中一个动点到达终点时另一个动点也停止运动,则△APQ的最大面积是(
).
A.10cm2
B.8cm2
C.16cm2
D.24cm2
8.足球运动员将足球沿与地面成一定角度的方向踢出,足球飞行的路线是一条抛物线,不考虑空气阻力,足球距离地面的高度h(单位:m)与足球被踢出后经过的时间t(单位:s)之间的关系如下表所示:
下列结论:
①足球距离地面的最大高度为20m;
②足球飞行路线的对称轴是直线t=4.5;
③足球被踢出9s时落地;
④足球被踢出1.5s时,距离地面的高度是11m.
其中结论正确的个数是(
).
A.1
B.2
C.3
D.4
二、填空题
9.小峰家要在一面长为38m的墙的一侧修建4个同样大小的猪圈,并在如图所示的5处各留1.5m宽的门,已知现有的材料共可修建长为41m的墙体,则能修建的4个猪圈的最大面积为
.
10.如图,线段AB的长为5,C为线段AB上一动点(与点A、B不重合),分别以AC、BC为斜边在AB的同侧作等腰直角三角形ACD和BCE,若AD=x,BE=y,那么x2+y2最小值是______.
11.如图是某公园一圆形喷水池,水流在各个方向沿形状相同的抛物线落下,建立如下图所示的坐标系,如果喷头所在处A(0,1.25),水流路线最高处M(1,2.25),则该抛物的解析式为
。如果不考虑其他因素,那么水池的半径至少要
m,才能使喷出的水流不至落到池外。
12.如图,四边形ABCD是矩形,A,B两点在x轴的正半轴上,C,D两点在抛物线y=-x2+6x上,设OA=m(0
13.某服装店购进单价为15元童装若干件,销售一段时间后发现:当销售价为25元时平均每天能售出8件,而当销售价每降低2元,平均每天能多售出4件,当每件的定价为__22__元时,该服装店平均每天的销售利润最大.
14.某公园草坪的防护栏由100段形状相同的抛物线形构件组成,为了牢固起见,每段护栏下每隔0.4m需要加设一根不锈钢的支柱,防护栏的最高点距底部0.5m(如图所示),则这条防护栏需要不锈钢支柱的总长度至少为
.
三、解答题
15.用长度一定的不锈钢材料设计成外观为矩形的框架(如图1,2所示的一种).
设竖档AB=x(m),请根据图案解答下列问题(题中的不锈钢材料总长度均指各图中所有黑线的长度和,所有横档和竖档分别与AD,AB平行):
(1)在图1中,如果不锈钢材料总长度为12m,当x为多少时,矩形框架ABCD的面积为3m2?
(2)在图2中,如果不锈钢材料总长度为12m,当x为多少时,矩形框架ABCD的面积S最大?最大面积是多少?
16.端午节前夕,三位同学到某超市调研一种进价为80元的粽子礼盒的销售情况,请根据小梅提供的信息,解答小慧和小杰提出的问题.(价格取正整数)
小梅:每盒定价100元,每天能卖出410盒,而且这种粽子礼盒的售价每上涨1元,其销售量减少10盒.
小慧:照你所说,如果要实现每天8580元的销售利润,并且薄利多销,那么该如何定价?小杰:8580元的销售利润是不是最大呢?如果不是,又该怎样定价才会使每天的销售利润最大?每天的最大销售利润是多少?
17.市场需求,某市电子玩具制造公司技术部研制开发一种新产品,年初上市后,公司经历了从亏损到盈利的过程.如图所示的二次函数图象(部分)刻画了该公司年初以来累积利润s(万元)与销售时间t(月)之间的关系(即前t个月的利润总和s和t之间的关系).根据图象提供的信息,解答下列问题:
(1)根据图象,求累积利润s(万元)关于时间t(月)的二次函数的表达式.
(2)截止到几月末,公司累积利润可达到6万元?
(3)第9个月公司所获利润是多少万元?
18.某超市销售一种商品,成本每千克40元,规定每千克售价不低于成本,且不高于80元.经市场调查,每天的销售量y(千克)与每千克售价x(元)满足一次函数关系,部分数据如下表所示:
(1)求y关于x的函数表达式.
(2)设商品每天的总利润为W(元),求W关于x的函数表达式(利润=收入-成本).
(3)试说明(2)中总利润W随售价x的变化而变化的情况,并指出售价为多少元时获得最大利润,最大利润是多少.
19.甲、乙两人进行羽毛球比赛,羽毛球飞行的路线为抛物线的一部分,如图所示,甲在O点正上方1m的P处发出一球,羽毛球飞行的高度y(m)与水平距离x(m)之间满足函数表达式y=a(x-4)2+h,已知点O与球网的水平距离为5m,球网的高度为1.55m.
(1)当a=-时,①求h的值.②通过计算判断此球能否过网.
(2)若甲发球过网后,羽毛球飞行到与点O的水平距离为7m,离地面的高度为m的Q处时,乙扣球成功,求a的值.
20.某商店销售一种商品,童威经市场调查发现:该商品的周销售量y(件)是售价x(元/件)的一次函数,其售价、周销售量、周销售利润w(元)的三组对应值如下表:
注:周销售利润=周销售量×(售价-进价)
(1)①求y关于x的函数解析式(不要求写出自变量的取值范围)
②该商品进价是_________元/件;当售价是________元/件时,周销售利润最大,最大利润是
__________元
(2)由于某种原因,该商品进价提高了m元/件(m>0),物价部门规定该商品售价不得超过65元/件,该商店在今后的销售中,周销售量与售价仍然满足(1)中的函数关系.若周销售最大利润是1400元,求m的值
参考答案
1.B
2.A
3.C
4.B
5.A
6.B.
7.C.
8.B.
9.答案为:9409/80.
10.答案为:.
11.答案为:y=-x2
+2x+1.25,
12.答案为:l=-2m2+8m+12
13.答案为:22
14.答案为:160.
15.解:(1)由题意得BC的长为(4-x)(m),
∴x(4-x)=3,
即x2-4x+3=0,解得x1=1,x2=3.
∴当x=1或3时,矩形框架ABCD的面积为3m2.
(2)由题意得AD=(12-4x)÷3=4-x,
∴S=x(4-x)=-
x2+4x=-(x-)2+3.
∴当x=时,矩形框架ABCD的面积最大,最大面积是3m2.
16.解:小慧:设定价为x元,利润为y元,
则销售量为410-10(x-100)=1410-10x,
由题意得y=(x-80)(1410-10x)=-10x2+2210x-112800,
当y=8580时,-10x2+2210x-112800=8580,
整理得x2-221x+12138=0,解得x=102或x=119.
∵当x=102时,销量为1410-1020=390,
当x=119时,销量为1410-1190=220,
∴若要达到8580元的利润,且薄利多销,此时的定价应为102元.
小杰:y=-10x2+2210x-112800=-10(x-)2+,
∵价格取整数,即x为整数,
∴当x=110或x=111时,y取得最大值,最大值为9300,
∴每天8580元的销售利润不是最大的,当定价为110元或111元时,每天的销售利润最大,最大销售利润为9300元.
17.解:(1)由图象可知抛物线顶点坐标为(2,-2),与x轴交点为(0,0),(4,0).
可设函数表达式为s=a(t-2)2-2.
将(0,0)代入得4a-2=0,解得a=.
∴s=(t-2)2-2.
(2)当累积利润达到6万元时,s=(t-2)2-2=6,解得t=6或-2(舍去).
∴截止到6月末公司累积利润可达到6万元.
(3)当t=9时,s=(t-2)2-2=(9-2)2-2=22.5(万元);
当t=8时,s=(t-2)2-2=(8-2)2-2=16(万元).
∵22.5-16=6.5(万元),
∴第9个月公司所获利润是6.5万元.
18.解:(1)设y关于x的函数表达式为y=kx+b.
由题意得,解得.
∴y关于x的函数表达式为y=-2x+200.
(2)W=(x-40)(-2x+200)=-2x2+280x-8000.
(3)∵W=-2x2+280x-8000=-2(x-70)2+1800,40≤x≤80,
∴当40≤x≤70时,W随x的增大而增大;
当70≤x≤80时,W随x的增大而减小;
当x=70时,W取得最大值,此时W=1800,
即售价为70元时获得最大利润,最大利润是1800元.
19.解:(1)①当a=-时,y=-
(x-4)2+h,
将点P(0,1)代入,得-×16+h=1,解得h=.
②把x=5代入y=-
(x-4)2+,得y=-×(5-4)2+=1.625,
∵1.625>1.55,
∴此球能过网.
(2)把(0,1),(7,)代入y=a(x-4)2+h,
得,解得.
∴a=-.
20.解:
同课章节目录
