第二十三章《旋转》同步专题八强化练习卷2021-2022学年九年级数学人教版上册(Word版 含答案)
文档属性
| 名称 | 第二十三章《旋转》同步专题八强化练习卷2021-2022学年九年级数学人教版上册(Word版 含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 270.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-07 00:00:00 | ||
图片预览




文档简介
人教版数学九年级上册同步专题八
《旋转》强化练习卷
一、选择题
1.将一副三角板按如图①的位置摆放,将△DEF绕点A(F)逆时针旋转60°后,得到如图②,测得CG=6,则AC长是(
)
A.6+2
B.9
C.10
D.6+6
2.如图,在Rt△ABC中,∠ACB=90°,∠B=60°,BC=2,∠A′B′C′可以由△ABC绕点C顺时针旋转得到,其中点A′与点A是对应点,点B′与点B是对应点,连接AB′,且A、B′、A′在同一条直线上,则AA′的长为(
)
A.4
B.6
C.3
D.3
3.如图,正方形ABCD的对角线相交于点O,Rt△OEF绕点O旋转,在旋转过程中,两个图形重叠部分的面积是正方形面积的(
)
A.
B.
C.
D.
4.如图所示,在等边△ABC中,点D是边AC上一点,连接BD,将△BCD绕着点B逆时针旋转60?,得到△BAE,连接ED,
则下列结论中:①AE∥BC;②∠DEB=60?;③∠ADE=∠BDC.
其中正确结论的序号是(
)
A.①②
B.①③
C.②③
D.只有①
5.如图已知在△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC的中点,两边PE、PF分别交AB和AC于点E、F.
给出以下五个结论正确的个数有( )
①AE=CF;
②∠APE=∠CPF;
③△BEP≌△AFP;
④△EPF是等腰直角三角形;
⑤当∠EPF在△ABC内绕顶点P旋转时(点E不与A、B重合),2S四边形AEPF=S△ABC.
A.2?????
B.3??????
C.4?????
D.5
6.如图,等边三角形ABC的边长为4,点O是△ABC的中心,∠FOG=120°,绕点O旋转∠FOG,分别交线段AB、BC于D、E两点,连接DE.
给出下列四个结论:
①OD=OE;
②S△ODE=S△BDE;
③四边形ODBE的面积始终等于;
④△BDE周长的最小值为6.
上述结论中正确的个数是(
)
A.1
B.2
C.3
D.4
7.如图,在4×4的正方形网格中,每个小正方形的顶点称为格点,左上角阴影部分是一个以格点为顶点的正方形(简称格点正方形).若再作一个格点正方形,并涂上阴影,使这两个格点正方形无重叠面积,且组成的图形是轴对称图形,又是中心对称图形,则这个格点正方形的作法共有( )
A.2种
B.3种
C.4种
D.5种
8.如图,△AOB为等腰三角形,顶点A的坐标(2,),底边OB在x轴上.将△AOB绕点B按顺时针方向旋转一定角度后得△A′O′B,点A的对应点A′在x轴上,则点O′坐标为(
)
A.(,)
B.(,)
C.(,)
D.(,4)
二、填空题
9.如图,边长为1的等边△ABO在平面直角坐标系的位置如图所示,点O为坐标原点,点A在x轴上,以点O为旋转中心,将△ABO按逆时针方向旋转60°,得到△OA′B′,
则点A′的坐标为
.
10.如图,已知直角三角形ABC中,∠C=90°,将△ABC绕点A逆时针旋转至△AED,使点C的对应点D恰好落在边AB上,E为点B的对应点.设∠BAC=α,则∠BED=
.(用含α的代数式表示)
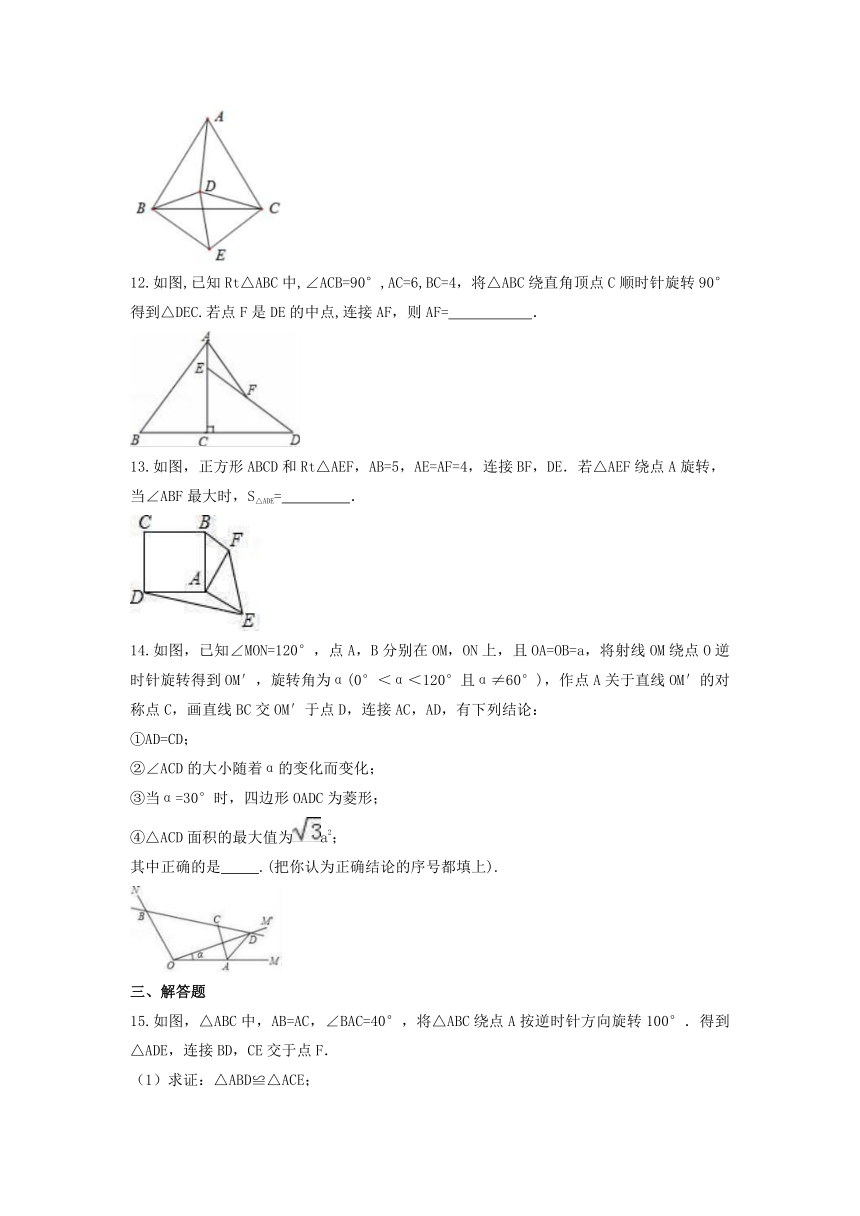
11.如图,已知正三角形ABC与正三角形CDE,若∠DBE=66°,则∠ADB度数为
.
12.如图,已知Rt△ABC中,∠ACB=90°,AC=6,BC=4,将△ABC绕直角顶点C顺时针旋转90°得到△DEC.若点F是DE的中点,连接AF,则AF=
.
13.如图,正方形ABCD和Rt△AEF,AB=5,AE=AF=4,连接BF,DE.若△AEF绕点A旋转,
当∠ABF最大时,S△ADE= ??
.
14.如图,已知∠MON=120°,点A,B分别在OM,ON上,且OA=OB=a,将射线OM绕点O逆时针旋转得到OM′,旋转角为α(0°<α<120°且α≠60°),作点A关于直线OM′的对称点C,画直线BC交OM′于点D,连接AC,AD,有下列结论:
①AD=CD;
②∠ACD的大小随着α的变化而变化;
③当α=30°时,四边形OADC为菱形;
④△ACD面积的最大值为a2;
其中正确的是
.(把你认为正确结论的序号都填上).
三、解答题
15.如图,△ABC中,AB=AC,∠BAC=40°,将△ABC绕点A按逆时针方向旋转100°.得到△ADE,连接BD,CE交于点F.
(1)求证:△ABD≌△ACE;
(2)求∠ACE的度数;
(3)求证:四边形ABFE是菱形.
16.如图所示,正方形ABCD的边长等于2,它绕顶点B按顺时针方向旋转得到正方形A′B′C′D′,在这个旋转过程中:
①旋转中心是什么?
②若旋转角为45°,边CD与A′D′交于F,求DF的长度.
17.(1)如图1,四边形ABCD中,AB=7,BC=3,∠ABC=∠ACD=∠ADC=45°,求BD的长;
(2)如图2,在(2)的条件下,当△ACD在线段AC的左侧时,求BD的长.
18.如图①是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成,在Rt△ABC中,已知直角边BC=5,AC=7,将四个直角三角形中边长为5的直角边分别向外延长一倍,得到如图②所示的“数学风车”.
⑴这个风车是中心对称图形吗?若是,指出这个风车至少需要绕着它的中心旋转多少度才能和它本身重合;
⑵求这个风车的外围周长(即求图②中的实线的长).
19.如图,点O是等边三角形ABC内的一点,∠BOC=150°,将△BOC绕点C按顺时针旋转得到△ADC,连接OD,OA.
(1)求∠ODC的度数;
(2)若OB=2,OC=3,求AO的长.
20.已知,△ABC中,∠ACB=90°,AC=BC,点D为BC边上的一点.
(1)以点C为旋转中心,将△ACD逆时针旋转90°,得到△BCE,请你画出旋转后的图形;
(2)延长AD交BE于点F,求证:AF⊥BE;
(3)若AC=,BF=1,连接CF,则CF的长度为_________.
21.如图,在正方形ABCD中,E、F是对角线BD上两点,且∠EAF=45°,将△ADF绕点A顺时针旋转90°后,得到△ABQ,连接EQ,求证:
(1)EA是∠QED的平分线;(2)EF2=BE2+DF2.
参考答案
1.A
2.B
3.A.
4.A;
5.D.
6.C.
7.C.
8.C
9.答案为:(﹣,﹣).
10.答案为:0.5α;
11.答案为:126°;
12.答案为:5.
13.答案为:6.
14.答案为:①③④.
15.(1)证明:∵△ABC绕点A按逆时针方向旋转100°,
∴∠BAC=∠DAE=40°,∴∠BAD=∠CAE=100°,
又∵AB=AC,∴AB=AC=AD=AE,
在△ABD与△ACE中
∴△ABD≌△ACE(SAS).
(2)解:∵∠CAE=100°,AC=AE,∴∠ACE===40°;
(3)证明:∵∠BAD=∠CAE=100°AB=AC=AD=AE,
∴∠ABD=∠ADB=∠ACE=∠AEC=40°.
∵∠BAE=∠BAD+∠DAE=140°,
∴∠BFE=360°﹣∠BAE﹣∠ABD﹣∠AEC=140°,∴∠BAE=∠BFE,
∴四边形ABFE是平行四边形,∵AB=AE,∴平行四边形ABFE是菱形.
16.解:①旋转中心为B点.②如图所示:
∵旋转角为45°,
∴∠ABA′=45°.
∵四边形ABCD为正方形,
∴∠ABD=45°,∠A′DF=45°.
∴∠ABA′=∠ABD.
∴点B、A′、D三点在一条直线上.
在Rt△ABD中,BD===2.
∵A′D=BD﹣BA′,
∴A′D=2﹣2.
在Rt△A′DF中,DF==4﹣2.
17.解:(1)将△ABD绕点A顺时针旋转90°得△AEC,连接EB,
则△ABE为等腰直角三角形,
BE=AB=7,∠ABF=45°,
∵∠ABC=45°,
∴∠EBC=90°,
∴BD=EC==
(2)将△ABD绕点A逆时针旋转90°得△AEC,则△ABE为等腰直角三角形,
BE=AB=7,
BD=EC=BE-BC=7-3
18.解:⑴这个风车是中心对称图形,
这个风车至少需要绕着它的中心旋转90度才能和它本身重合;
⑵风车的其中一个直角三角形的较短直角边长为5,
较长直角边长为7+5=12,
则斜边长为13,
所以这个风车的外围周长为4×(5+13)=4×18=72.
19.解:(Ⅰ)由旋转的性质得,CD=CO,∠ACD=∠BCO,
∵∠ACB=60°,
∴∠DCO=60°,
∴△OCD为等边三角形,
∴∠ODC=60°;
(Ⅱ)由旋转的性质得,AD=OB=2,
∵△OCD为等边三角形,
∴OD=OC=3,
∵∠BOC=150°,∠ODC=60°,
∴∠ADO=90°,
在Rt△AOD中,由勾股定理得:AO==.
20.(1)解:旋转后的图形如图所示.
(2)证明:∵△ACD≌△BCE,
∴∠CAD=∠CBE,
∵∠CAD+∠ADC=90°,∠ADC=∠BDF,
∴∠BDF+∠DBF=90°,
∴∠DFB=90°,
∴AF⊥BE.
(3)作CM⊥BE于M,CN⊥AF于N.
∵∠ANC=∠BMC=90°,∠CAN=∠CBM,AC=BC,
∴△ACN≌△BCM(AAS),
∴CN=CM,
∵∠CMF=∠MFN=∠FNC=90°,
∴四边形CMFN是矩形,
∵CM=CN,
∴四边形CMFN是正方形,设CN=CM=MF=FN=a,
在Rt△BCM中,∵BC2=CM2+BM2,
∴3=a2+(a+1)2,
∴a2+a﹣1=0,
∴a=或(舍弃),
∴CF=CM=a=.
21.证明:(1)∵将△ADF绕点A顺时针旋转90°后,得到△ABQ,
∴QB=DF,AQ=AF,∠ABQ=∠ADF=45°,
在△AQE和△AFE中,
∴△AQE≌△AFE(SAS),
∴∠AEQ=∠AEF,
∴EA是∠QED的平分线;
(2)由(1)得△AQE≌△AFE,
∴QE=EF,
在Rt△QBE中,QB2+BE2=QE2,则EF2=BE2+DF2.
《旋转》强化练习卷
一、选择题
1.将一副三角板按如图①的位置摆放,将△DEF绕点A(F)逆时针旋转60°后,得到如图②,测得CG=6,则AC长是(
)
A.6+2
B.9
C.10
D.6+6
2.如图,在Rt△ABC中,∠ACB=90°,∠B=60°,BC=2,∠A′B′C′可以由△ABC绕点C顺时针旋转得到,其中点A′与点A是对应点,点B′与点B是对应点,连接AB′,且A、B′、A′在同一条直线上,则AA′的长为(
)
A.4
B.6
C.3
D.3
3.如图,正方形ABCD的对角线相交于点O,Rt△OEF绕点O旋转,在旋转过程中,两个图形重叠部分的面积是正方形面积的(
)
A.
B.
C.
D.
4.如图所示,在等边△ABC中,点D是边AC上一点,连接BD,将△BCD绕着点B逆时针旋转60?,得到△BAE,连接ED,
则下列结论中:①AE∥BC;②∠DEB=60?;③∠ADE=∠BDC.
其中正确结论的序号是(
)
A.①②
B.①③
C.②③
D.只有①
5.如图已知在△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC的中点,两边PE、PF分别交AB和AC于点E、F.
给出以下五个结论正确的个数有( )
①AE=CF;
②∠APE=∠CPF;
③△BEP≌△AFP;
④△EPF是等腰直角三角形;
⑤当∠EPF在△ABC内绕顶点P旋转时(点E不与A、B重合),2S四边形AEPF=S△ABC.
A.2?????
B.3??????
C.4?????
D.5
6.如图,等边三角形ABC的边长为4,点O是△ABC的中心,∠FOG=120°,绕点O旋转∠FOG,分别交线段AB、BC于D、E两点,连接DE.
给出下列四个结论:
①OD=OE;
②S△ODE=S△BDE;
③四边形ODBE的面积始终等于;
④△BDE周长的最小值为6.
上述结论中正确的个数是(
)
A.1
B.2
C.3
D.4
7.如图,在4×4的正方形网格中,每个小正方形的顶点称为格点,左上角阴影部分是一个以格点为顶点的正方形(简称格点正方形).若再作一个格点正方形,并涂上阴影,使这两个格点正方形无重叠面积,且组成的图形是轴对称图形,又是中心对称图形,则这个格点正方形的作法共有( )
A.2种
B.3种
C.4种
D.5种
8.如图,△AOB为等腰三角形,顶点A的坐标(2,),底边OB在x轴上.将△AOB绕点B按顺时针方向旋转一定角度后得△A′O′B,点A的对应点A′在x轴上,则点O′坐标为(
)
A.(,)
B.(,)
C.(,)
D.(,4)
二、填空题
9.如图,边长为1的等边△ABO在平面直角坐标系的位置如图所示,点O为坐标原点,点A在x轴上,以点O为旋转中心,将△ABO按逆时针方向旋转60°,得到△OA′B′,
则点A′的坐标为
.
10.如图,已知直角三角形ABC中,∠C=90°,将△ABC绕点A逆时针旋转至△AED,使点C的对应点D恰好落在边AB上,E为点B的对应点.设∠BAC=α,则∠BED=
.(用含α的代数式表示)
11.如图,已知正三角形ABC与正三角形CDE,若∠DBE=66°,则∠ADB度数为
.
12.如图,已知Rt△ABC中,∠ACB=90°,AC=6,BC=4,将△ABC绕直角顶点C顺时针旋转90°得到△DEC.若点F是DE的中点,连接AF,则AF=
.
13.如图,正方形ABCD和Rt△AEF,AB=5,AE=AF=4,连接BF,DE.若△AEF绕点A旋转,
当∠ABF最大时,S△ADE= ??
.
14.如图,已知∠MON=120°,点A,B分别在OM,ON上,且OA=OB=a,将射线OM绕点O逆时针旋转得到OM′,旋转角为α(0°<α<120°且α≠60°),作点A关于直线OM′的对称点C,画直线BC交OM′于点D,连接AC,AD,有下列结论:
①AD=CD;
②∠ACD的大小随着α的变化而变化;
③当α=30°时,四边形OADC为菱形;
④△ACD面积的最大值为a2;
其中正确的是
.(把你认为正确结论的序号都填上).
三、解答题
15.如图,△ABC中,AB=AC,∠BAC=40°,将△ABC绕点A按逆时针方向旋转100°.得到△ADE,连接BD,CE交于点F.
(1)求证:△ABD≌△ACE;
(2)求∠ACE的度数;
(3)求证:四边形ABFE是菱形.
16.如图所示,正方形ABCD的边长等于2,它绕顶点B按顺时针方向旋转得到正方形A′B′C′D′,在这个旋转过程中:
①旋转中心是什么?
②若旋转角为45°,边CD与A′D′交于F,求DF的长度.
17.(1)如图1,四边形ABCD中,AB=7,BC=3,∠ABC=∠ACD=∠ADC=45°,求BD的长;
(2)如图2,在(2)的条件下,当△ACD在线段AC的左侧时,求BD的长.
18.如图①是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成,在Rt△ABC中,已知直角边BC=5,AC=7,将四个直角三角形中边长为5的直角边分别向外延长一倍,得到如图②所示的“数学风车”.
⑴这个风车是中心对称图形吗?若是,指出这个风车至少需要绕着它的中心旋转多少度才能和它本身重合;
⑵求这个风车的外围周长(即求图②中的实线的长).
19.如图,点O是等边三角形ABC内的一点,∠BOC=150°,将△BOC绕点C按顺时针旋转得到△ADC,连接OD,OA.
(1)求∠ODC的度数;
(2)若OB=2,OC=3,求AO的长.
20.已知,△ABC中,∠ACB=90°,AC=BC,点D为BC边上的一点.
(1)以点C为旋转中心,将△ACD逆时针旋转90°,得到△BCE,请你画出旋转后的图形;
(2)延长AD交BE于点F,求证:AF⊥BE;
(3)若AC=,BF=1,连接CF,则CF的长度为_________.
21.如图,在正方形ABCD中,E、F是对角线BD上两点,且∠EAF=45°,将△ADF绕点A顺时针旋转90°后,得到△ABQ,连接EQ,求证:
(1)EA是∠QED的平分线;(2)EF2=BE2+DF2.
参考答案
1.A
2.B
3.A.
4.A;
5.D.
6.C.
7.C.
8.C
9.答案为:(﹣,﹣).
10.答案为:0.5α;
11.答案为:126°;
12.答案为:5.
13.答案为:6.
14.答案为:①③④.
15.(1)证明:∵△ABC绕点A按逆时针方向旋转100°,
∴∠BAC=∠DAE=40°,∴∠BAD=∠CAE=100°,
又∵AB=AC,∴AB=AC=AD=AE,
在△ABD与△ACE中
∴△ABD≌△ACE(SAS).
(2)解:∵∠CAE=100°,AC=AE,∴∠ACE===40°;
(3)证明:∵∠BAD=∠CAE=100°AB=AC=AD=AE,
∴∠ABD=∠ADB=∠ACE=∠AEC=40°.
∵∠BAE=∠BAD+∠DAE=140°,
∴∠BFE=360°﹣∠BAE﹣∠ABD﹣∠AEC=140°,∴∠BAE=∠BFE,
∴四边形ABFE是平行四边形,∵AB=AE,∴平行四边形ABFE是菱形.
16.解:①旋转中心为B点.②如图所示:
∵旋转角为45°,
∴∠ABA′=45°.
∵四边形ABCD为正方形,
∴∠ABD=45°,∠A′DF=45°.
∴∠ABA′=∠ABD.
∴点B、A′、D三点在一条直线上.
在Rt△ABD中,BD===2.
∵A′D=BD﹣BA′,
∴A′D=2﹣2.
在Rt△A′DF中,DF==4﹣2.
17.解:(1)将△ABD绕点A顺时针旋转90°得△AEC,连接EB,
则△ABE为等腰直角三角形,
BE=AB=7,∠ABF=45°,
∵∠ABC=45°,
∴∠EBC=90°,
∴BD=EC==
(2)将△ABD绕点A逆时针旋转90°得△AEC,则△ABE为等腰直角三角形,
BE=AB=7,
BD=EC=BE-BC=7-3
18.解:⑴这个风车是中心对称图形,
这个风车至少需要绕着它的中心旋转90度才能和它本身重合;
⑵风车的其中一个直角三角形的较短直角边长为5,
较长直角边长为7+5=12,
则斜边长为13,
所以这个风车的外围周长为4×(5+13)=4×18=72.
19.解:(Ⅰ)由旋转的性质得,CD=CO,∠ACD=∠BCO,
∵∠ACB=60°,
∴∠DCO=60°,
∴△OCD为等边三角形,
∴∠ODC=60°;
(Ⅱ)由旋转的性质得,AD=OB=2,
∵△OCD为等边三角形,
∴OD=OC=3,
∵∠BOC=150°,∠ODC=60°,
∴∠ADO=90°,
在Rt△AOD中,由勾股定理得:AO==.
20.(1)解:旋转后的图形如图所示.
(2)证明:∵△ACD≌△BCE,
∴∠CAD=∠CBE,
∵∠CAD+∠ADC=90°,∠ADC=∠BDF,
∴∠BDF+∠DBF=90°,
∴∠DFB=90°,
∴AF⊥BE.
(3)作CM⊥BE于M,CN⊥AF于N.
∵∠ANC=∠BMC=90°,∠CAN=∠CBM,AC=BC,
∴△ACN≌△BCM(AAS),
∴CN=CM,
∵∠CMF=∠MFN=∠FNC=90°,
∴四边形CMFN是矩形,
∵CM=CN,
∴四边形CMFN是正方形,设CN=CM=MF=FN=a,
在Rt△BCM中,∵BC2=CM2+BM2,
∴3=a2+(a+1)2,
∴a2+a﹣1=0,
∴a=或(舍弃),
∴CF=CM=a=.
21.证明:(1)∵将△ADF绕点A顺时针旋转90°后,得到△ABQ,
∴QB=DF,AQ=AF,∠ABQ=∠ADF=45°,
在△AQE和△AFE中,
∴△AQE≌△AFE(SAS),
∴∠AEQ=∠AEF,
∴EA是∠QED的平分线;
(2)由(1)得△AQE≌△AFE,
∴QE=EF,
在Rt△QBE中,QB2+BE2=QE2,则EF2=BE2+DF2.
同课章节目录
