23.1.1认识图形的旋转能力提升卷 2021-2022学年人教版九年级数学上册(Word版 含答案)
文档属性
| 名称 | 23.1.1认识图形的旋转能力提升卷 2021-2022学年人教版九年级数学上册(Word版 含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 194.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-07 09:26:13 | ||
图片预览


文档简介
人教版九年级数学上册
23.1.1 认识图形的旋转
能力提升卷
一、选择题(共8小题,4
8=32)
1.
下列运动形式属于旋转的是( )
A.在空中上升的氢气球
B.飞驰的火车
C.时钟上钟摆的摆动
D.运动员掷出的标枪
2.
下列图形绕某一点旋转一定角度都能与原图形重合,其中旋转角度最小的是( )
3.
如图,将△OAB绕点O逆时针旋转70°到△OCD的位置,若∠AOB=40°,则∠AOD=(
)
A.45°
B.40°
C.35°
D.30°
4.
如图,在△ABC中,∠ACB=90°,将△ABC绕点C顺时针旋转得到△DEC,使点B的对应点E恰好落在边AC上,点A的对应点为D,延长DE交AB于点F,则下列结论一定正确的是(
)
A.AC=DE
B.BC=EF
C.∠AEF=∠D
D.AB⊥DF
5.
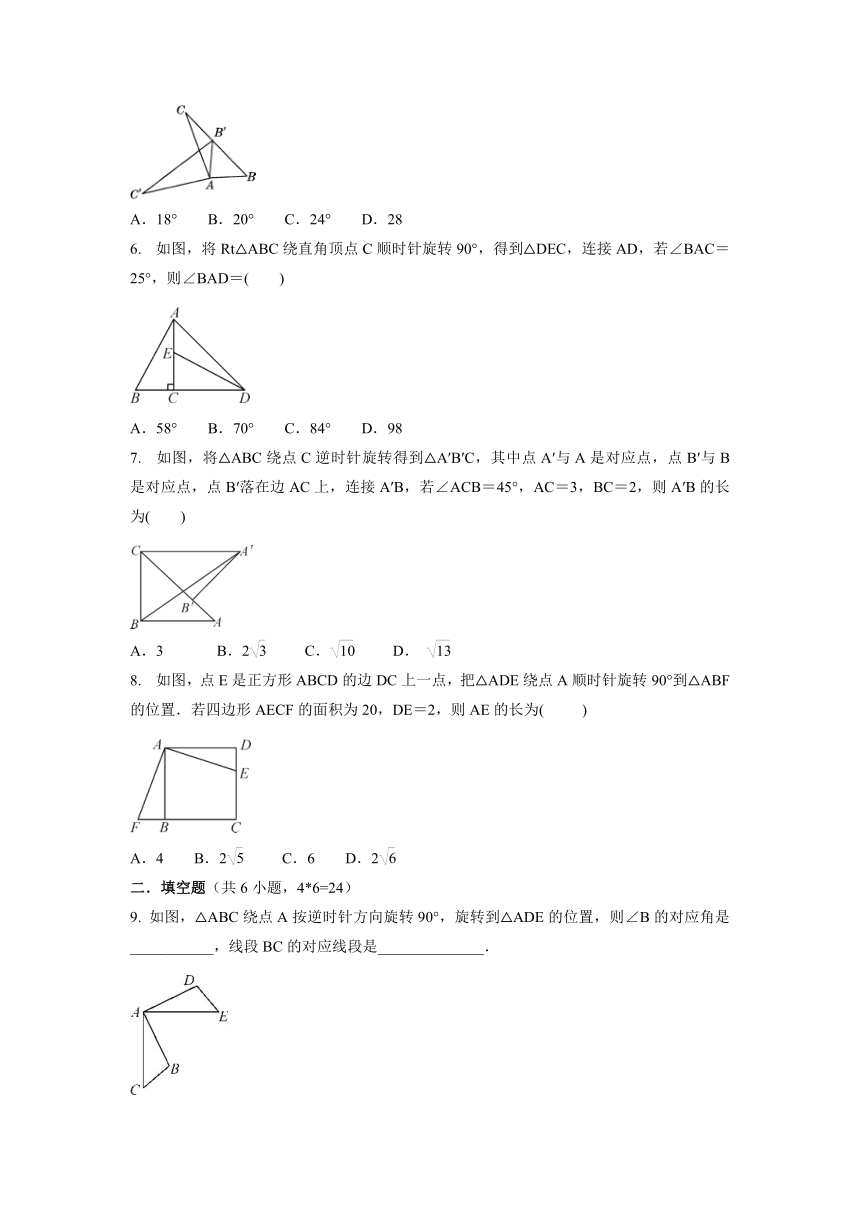
如图,在△ABC中,∠BAC=108°,将△ABC绕点A按逆时针方向旋转得到△AB′C′.若点B′恰好落在BC边上,且AB′=CB′,则∠C′的度数为( )
A.18°
B.20°
C.24°
D.28
6.
如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△DEC,连接AD,若∠BAC=25°,则∠BAD=( )
A.58°
B.70°
C.84°
D.98
7.
如图,将△ABC绕点C逆时针旋转得到△A′B′C,其中点A′与A是对应点,点B′与B是对应点,点B′落在边AC上,连接A′B,若∠ACB=45°,AC=3,BC=2,则A′B的长为( )
A.3
B.2
C.
D.
8.
如图,点E是正方形ABCD的边DC上一点,把△ADE绕点A顺时针旋转90°到△ABF的位置.若四边形AECF的面积为20,DE=2,则AE的长为(
)
A.4
B.2
C.6
D.2
二.填空题(共6小题,4
6=24)
9.
如图,△ABC绕点A按逆时针方向旋转90°,旋转到△ADE的位置,则∠B的对应角是___________,线段BC的对应线段是______________.
10.
如图,点A,B,C,D,O都在方格纸的格点上,若△COD是由△AOB绕点O按顺时针方向旋转而得到的,则旋转的角度为___________.
11.
如图,在Rt△ABC中,∠BAC=90°,AB=2.将△ABC绕点A按顺时针方向旋转至△AB1C1的位置,点B1恰好落在边BC的中点处,则CC1的长为________________.
12.
如图,在Rt△ABC中,∠ACB=90°,AC=5
cm,BC=12
cm,将△ABC绕点B顺时针旋转60°,得到△BDE,连接DC交AB于点F,则△ACF与△BDF的周长之和为_______cm.
13.
在△ABC中,∠B=45°,∠C=60°,将△ABC绕点A旋转30°后得到△AB1C1,则∠BAC1=_________.
14.
如图,在正方形ABCD中,AD=2,把边BC绕点B逆时针旋转30°得到线段BP,连接AP并延长交CD于点E,连接PC,则△PCE的面积为_________.
三.解答题(共5小题,
44分)
15.(6分)
如图,在菱形ABCD中,∠A=110°,点E是菱形ABCD内一点,连接CE绕点C顺时针旋转110°,得到线段CF,连接BE,DF,若∠E=86°,求∠F的度数.
16.(8分)
如图,△ABC,△ECD都是等边三角形,BE与AD有什么关系?∠DFE的度数为多少?请你用旋转的性质说明理由.
17.(8分)
如图,已知AC⊥BC,垂足为C,AC=4,BC=3,将线段AC绕点A按逆时针方向旋转60°,得到线段AD,连接DC,DB.
求线段DB的长度.
18.(10分)
如图,点M,N分别在正方形ABCD的边BC,CD上,且∠MAN=45°.把△ADN绕点A顺时针旋转90°得到△ABE.
(1)求证:△AEM≌△ANM;
(2)若BM=3,DN=2,求正方形ABCD的边长.
19.(12分)
如图,在△ABC中,∠ACB=90°,AC=BC,D是AB边上一点(点D与A,B不重合),连接CD,将线段CD绕点C按逆时针方向旋转90°得到线段CE,连接DE交BC于点F,连接BE.
(1)求证:△ACD≌△BCE;
(2)当AD=BF时,求∠BEF的度数;
(3)求证:DE2=BD2+AD2.
参考答案
1-4CCDD
5-8CBDD
9.
∠D,DE
10.
90°
11.
2
12.
42
13.
105°或45°
14.
9-5
15.
解:∵四边形ABCD是菱形,∴BC=CD,∠BCD=∠A=110°,由旋转的性质知,CE=CF,∠ECF=∠BCD=110°,∴∠BCE=∠DCF=110°-∠DCE,在△BCE和△DCF中,∴△BCE≌△DCF(SAS),∴∠F=∠E=86°
16.
解:BE=AD,∠DFE=60°.理由:∵△ABC和△ECD都是等边三角形,∴∠ACB=∠DCE=60°,∴∠ACB+∠BCD=∠DCE+∠BCD,即∠ACD=∠BAE,∴△ACD是△BCE绕点C顺时针旋转60°得到的,∴△BCE≌△ACD,∴BE=AD,∴∠CBE=∠CAD,∴∠DFE=∠AFB=180°-(∠FAB+∠ABF)=180°-(∠BAC-∠CAD+∠ABC+∠CBE)=180°-2∠ABC=60°
17.
解:如图,作DE⊥BC于点E.∵△ACD是等边三角形,∴∠ACD=60°,又∵AC⊥BC,∴∠DCE=∠ACB-∠ACD=90°-60°=30°,∴在Rt△CDE中,DE=DC=2,由勾股定理得CE=2,∴BE=BC-CE=3-2=.∴Rt△BDE中,BD===
18.
解:(1)证明:由旋转的性质,得△ADN≌△ABE,∴∠DAN=∠BAE,AN=AE,∠D=∠ABE=90°,∵四边形ABCD为正方形,∴∠ABC=90°,∠DAB=90°,∴∠ABC+∠ABE=180°,∴E,B,C三点共线,∵∠MAN=45°,∴∠MAE=∠BAE+∠BAM=∠DAN+∠BAM=45°,∴∠MAE=∠MAN,∵MA=MA,∴△AEM≌△ANM(SAS)
(2)设CD=BC=x,则CM=x-3,CN=x-2,∵△AEM≌△ANM,∴EM=MN,∵BE=DN,∴MN=BM+BE=BM+DN=5,∵∠C=90°,∴MN2=CN2+CM2,∴25=(x-2)2+(x-3)2,解得x=6或-1(舍弃),∴正方形ABCD的边长为6
19.
(1)证明:由题意可知CD=CE,∠DCE=90°.
∵∠ACB=90°,∴∠DCE=∠ACB.
∵∠ACD=∠ACB-∠DCB,∠BCE=∠DCE-∠DCB,∴∠ACD=∠BCE.
在△ACD和△BCE中,∴△ACD≌△BCE(SAS).
(2)∵∠ACB=90°,AC=BC,∴∠A=45°.
由(1)知△ACD≌△BCE,
∴∠A=∠CBE=45°,AD=BE.
∵AD=BF,∴BE=BF.
∴∠BEF==67.5°.
(3)证明:由(1)知△ACD≌△BCE,∴∠A=∠CBE,AD=BE.
∵∠ACB=90°,∴∠A+∠CBA=90°.
∴∠CBE+∠CBA=90°.
∴∠EBD=90°.
∴DE2=BD2+BE2.
∴DE2=BD2+AD2.
23.1.1 认识图形的旋转
能力提升卷
一、选择题(共8小题,4
8=32)
1.
下列运动形式属于旋转的是( )
A.在空中上升的氢气球
B.飞驰的火车
C.时钟上钟摆的摆动
D.运动员掷出的标枪
2.
下列图形绕某一点旋转一定角度都能与原图形重合,其中旋转角度最小的是( )
3.
如图,将△OAB绕点O逆时针旋转70°到△OCD的位置,若∠AOB=40°,则∠AOD=(
)
A.45°
B.40°
C.35°
D.30°
4.
如图,在△ABC中,∠ACB=90°,将△ABC绕点C顺时针旋转得到△DEC,使点B的对应点E恰好落在边AC上,点A的对应点为D,延长DE交AB于点F,则下列结论一定正确的是(
)
A.AC=DE
B.BC=EF
C.∠AEF=∠D
D.AB⊥DF
5.
如图,在△ABC中,∠BAC=108°,将△ABC绕点A按逆时针方向旋转得到△AB′C′.若点B′恰好落在BC边上,且AB′=CB′,则∠C′的度数为( )
A.18°
B.20°
C.24°
D.28
6.
如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△DEC,连接AD,若∠BAC=25°,则∠BAD=( )
A.58°
B.70°
C.84°
D.98
7.
如图,将△ABC绕点C逆时针旋转得到△A′B′C,其中点A′与A是对应点,点B′与B是对应点,点B′落在边AC上,连接A′B,若∠ACB=45°,AC=3,BC=2,则A′B的长为( )
A.3
B.2
C.
D.
8.
如图,点E是正方形ABCD的边DC上一点,把△ADE绕点A顺时针旋转90°到△ABF的位置.若四边形AECF的面积为20,DE=2,则AE的长为(
)
A.4
B.2
C.6
D.2
二.填空题(共6小题,4
6=24)
9.
如图,△ABC绕点A按逆时针方向旋转90°,旋转到△ADE的位置,则∠B的对应角是___________,线段BC的对应线段是______________.
10.
如图,点A,B,C,D,O都在方格纸的格点上,若△COD是由△AOB绕点O按顺时针方向旋转而得到的,则旋转的角度为___________.
11.
如图,在Rt△ABC中,∠BAC=90°,AB=2.将△ABC绕点A按顺时针方向旋转至△AB1C1的位置,点B1恰好落在边BC的中点处,则CC1的长为________________.
12.
如图,在Rt△ABC中,∠ACB=90°,AC=5
cm,BC=12
cm,将△ABC绕点B顺时针旋转60°,得到△BDE,连接DC交AB于点F,则△ACF与△BDF的周长之和为_______cm.
13.
在△ABC中,∠B=45°,∠C=60°,将△ABC绕点A旋转30°后得到△AB1C1,则∠BAC1=_________.
14.
如图,在正方形ABCD中,AD=2,把边BC绕点B逆时针旋转30°得到线段BP,连接AP并延长交CD于点E,连接PC,则△PCE的面积为_________.
三.解答题(共5小题,
44分)
15.(6分)
如图,在菱形ABCD中,∠A=110°,点E是菱形ABCD内一点,连接CE绕点C顺时针旋转110°,得到线段CF,连接BE,DF,若∠E=86°,求∠F的度数.
16.(8分)
如图,△ABC,△ECD都是等边三角形,BE与AD有什么关系?∠DFE的度数为多少?请你用旋转的性质说明理由.
17.(8分)
如图,已知AC⊥BC,垂足为C,AC=4,BC=3,将线段AC绕点A按逆时针方向旋转60°,得到线段AD,连接DC,DB.
求线段DB的长度.
18.(10分)
如图,点M,N分别在正方形ABCD的边BC,CD上,且∠MAN=45°.把△ADN绕点A顺时针旋转90°得到△ABE.
(1)求证:△AEM≌△ANM;
(2)若BM=3,DN=2,求正方形ABCD的边长.
19.(12分)
如图,在△ABC中,∠ACB=90°,AC=BC,D是AB边上一点(点D与A,B不重合),连接CD,将线段CD绕点C按逆时针方向旋转90°得到线段CE,连接DE交BC于点F,连接BE.
(1)求证:△ACD≌△BCE;
(2)当AD=BF时,求∠BEF的度数;
(3)求证:DE2=BD2+AD2.
参考答案
1-4CCDD
5-8CBDD
9.
∠D,DE
10.
90°
11.
2
12.
42
13.
105°或45°
14.
9-5
15.
解:∵四边形ABCD是菱形,∴BC=CD,∠BCD=∠A=110°,由旋转的性质知,CE=CF,∠ECF=∠BCD=110°,∴∠BCE=∠DCF=110°-∠DCE,在△BCE和△DCF中,∴△BCE≌△DCF(SAS),∴∠F=∠E=86°
16.
解:BE=AD,∠DFE=60°.理由:∵△ABC和△ECD都是等边三角形,∴∠ACB=∠DCE=60°,∴∠ACB+∠BCD=∠DCE+∠BCD,即∠ACD=∠BAE,∴△ACD是△BCE绕点C顺时针旋转60°得到的,∴△BCE≌△ACD,∴BE=AD,∴∠CBE=∠CAD,∴∠DFE=∠AFB=180°-(∠FAB+∠ABF)=180°-(∠BAC-∠CAD+∠ABC+∠CBE)=180°-2∠ABC=60°
17.
解:如图,作DE⊥BC于点E.∵△ACD是等边三角形,∴∠ACD=60°,又∵AC⊥BC,∴∠DCE=∠ACB-∠ACD=90°-60°=30°,∴在Rt△CDE中,DE=DC=2,由勾股定理得CE=2,∴BE=BC-CE=3-2=.∴Rt△BDE中,BD===
18.
解:(1)证明:由旋转的性质,得△ADN≌△ABE,∴∠DAN=∠BAE,AN=AE,∠D=∠ABE=90°,∵四边形ABCD为正方形,∴∠ABC=90°,∠DAB=90°,∴∠ABC+∠ABE=180°,∴E,B,C三点共线,∵∠MAN=45°,∴∠MAE=∠BAE+∠BAM=∠DAN+∠BAM=45°,∴∠MAE=∠MAN,∵MA=MA,∴△AEM≌△ANM(SAS)
(2)设CD=BC=x,则CM=x-3,CN=x-2,∵△AEM≌△ANM,∴EM=MN,∵BE=DN,∴MN=BM+BE=BM+DN=5,∵∠C=90°,∴MN2=CN2+CM2,∴25=(x-2)2+(x-3)2,解得x=6或-1(舍弃),∴正方形ABCD的边长为6
19.
(1)证明:由题意可知CD=CE,∠DCE=90°.
∵∠ACB=90°,∴∠DCE=∠ACB.
∵∠ACD=∠ACB-∠DCB,∠BCE=∠DCE-∠DCB,∴∠ACD=∠BCE.
在△ACD和△BCE中,∴△ACD≌△BCE(SAS).
(2)∵∠ACB=90°,AC=BC,∴∠A=45°.
由(1)知△ACD≌△BCE,
∴∠A=∠CBE=45°,AD=BE.
∵AD=BF,∴BE=BF.
∴∠BEF==67.5°.
(3)证明:由(1)知△ACD≌△BCE,∴∠A=∠CBE,AD=BE.
∵∠ACB=90°,∴∠A+∠CBA=90°.
∴∠CBE+∠CBA=90°.
∴∠EBD=90°.
∴DE2=BD2+BE2.
∴DE2=BD2+AD2.
同课章节目录
