11.2.1三角形的内角课堂同步习题2021-2022学年八年级数学人教版上册(Word版 含答案)
文档属性
| 名称 | 11.2.1三角形的内角课堂同步习题2021-2022学年八年级数学人教版上册(Word版 含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 311.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-07 09:28:24 | ||
图片预览



文档简介
2021-2022学年初中数学八年级上册课堂同步(人教版)
11.2.1三角形的内角
时间:60分钟
一、单选题
1.具备下列条件的中,不是直角三角形的是(
)
A.
B.
C.
D.
2.已知三角形的一个内角是另一个内角的,是第三个内角的,则这个三角形各内角的度数分别为(
)
A.60°,90°,75°
B.48°,72°,60°
C.48°,32°,38°
D.40°,50°,90°
3.如图,BD平分∠ABC,CD⊥BD,D为垂足,∠C=55°,则∠ABC的度数是( )
A.35°
B.55°
C.60°
D.70°
4.如图,已知.则结论①;②平分;③;④.正确的是(
)
A.①②③
B.①②④
C.①③④
D.②③④
5.如图,△ABC中,∠ACB=90°,沿CD折叠△CBD,使点B恰好落在AC边上的点E处,若∠A=25°,则∠BDC等于( )
A.44°
B.60°
C.67°
D.70°
6.如图,将沿MN折叠,使,点A的对应点为点,若,,则的度数是(
)
A.
B.
C.
D.
7.如图,在△ABC中,AD平分∠BAC且与BC相交于点D,∠B=40°,∠BAD=30°,则∠C的度数是( )
A.70°
B.80°
C.100°
D.110°
8.如图,AB∥CD,EF与AB、CD分别相交于点E、F,EP⊥EF,与∠EFD的平分线FP相交于点P,且∠BEP=50°,则∠EPF=(
)度.
A.70
B.65
C.60
D.55
二、填空题
9.将一副直角三角板如图放置,使含30°角的三角板的短直角边和含45°角的三角板的一条直角边重合,则∠1的度数为_______度.
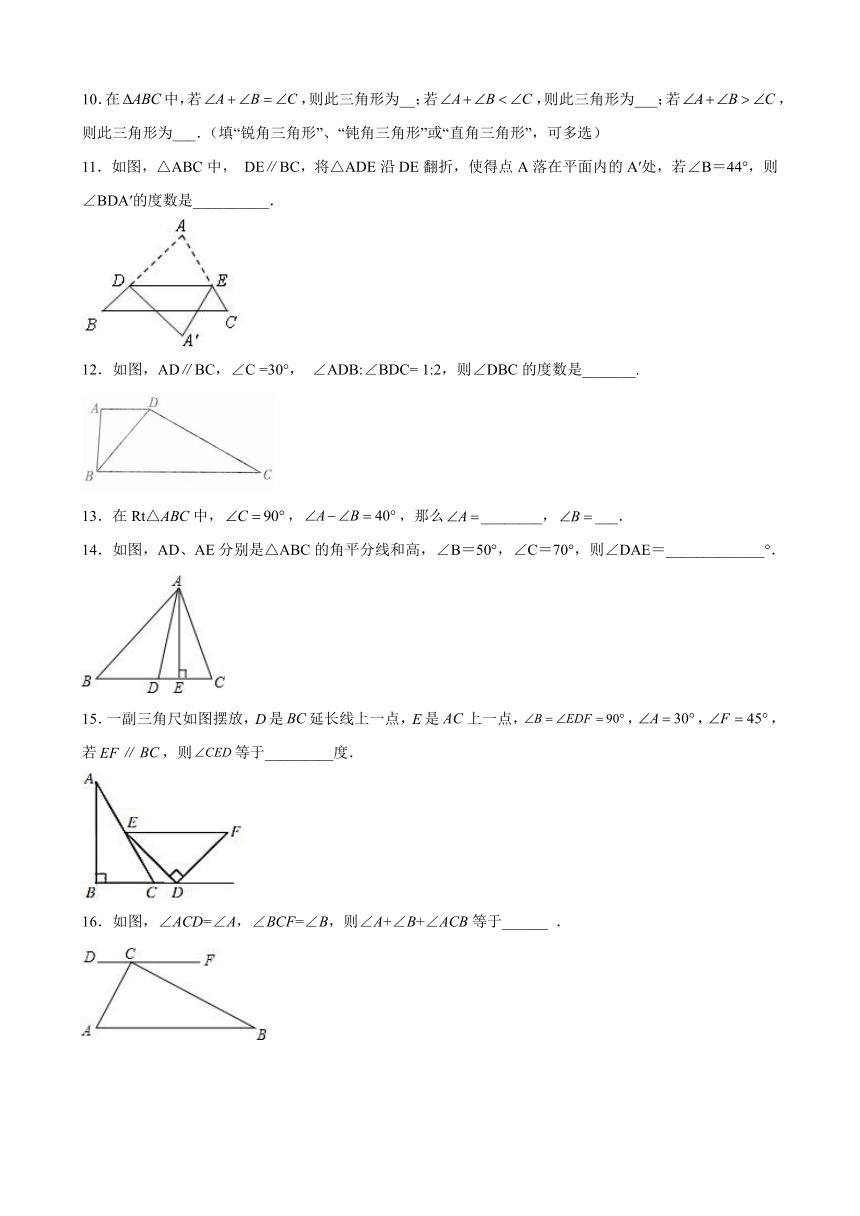
10.在中,若,则此三角形为__;若,则此三角形为___;若,则此三角形为___.(填“锐角三角形”、“钝角三角形”或“直角三角形”,可多选)
11.如图,△ABC中,
DE∥BC,将△ADE沿DE翻折,使得点A落在平面内的A′处,若∠B=44°,则∠BDA′的度数是__________.
12.如图,AD∥BC,∠C
=30°,
∠ADB:∠BDC=
1:2,则∠DBC的度数是_______.
13.在Rt△ABC中,,,那么________,___.
14.如图,AD、AE分别是△ABC的角平分线和高,∠B=50°,∠C=70°,则∠DAE=_____________°.
15.一副三角尺如图摆放,是延长线上一点,是上一点,,,,若∥,则等于_________度.
16.如图,∠ACD=∠A,∠BCF=∠B,则∠A+∠B+∠ACB等于______
.
三、解答题
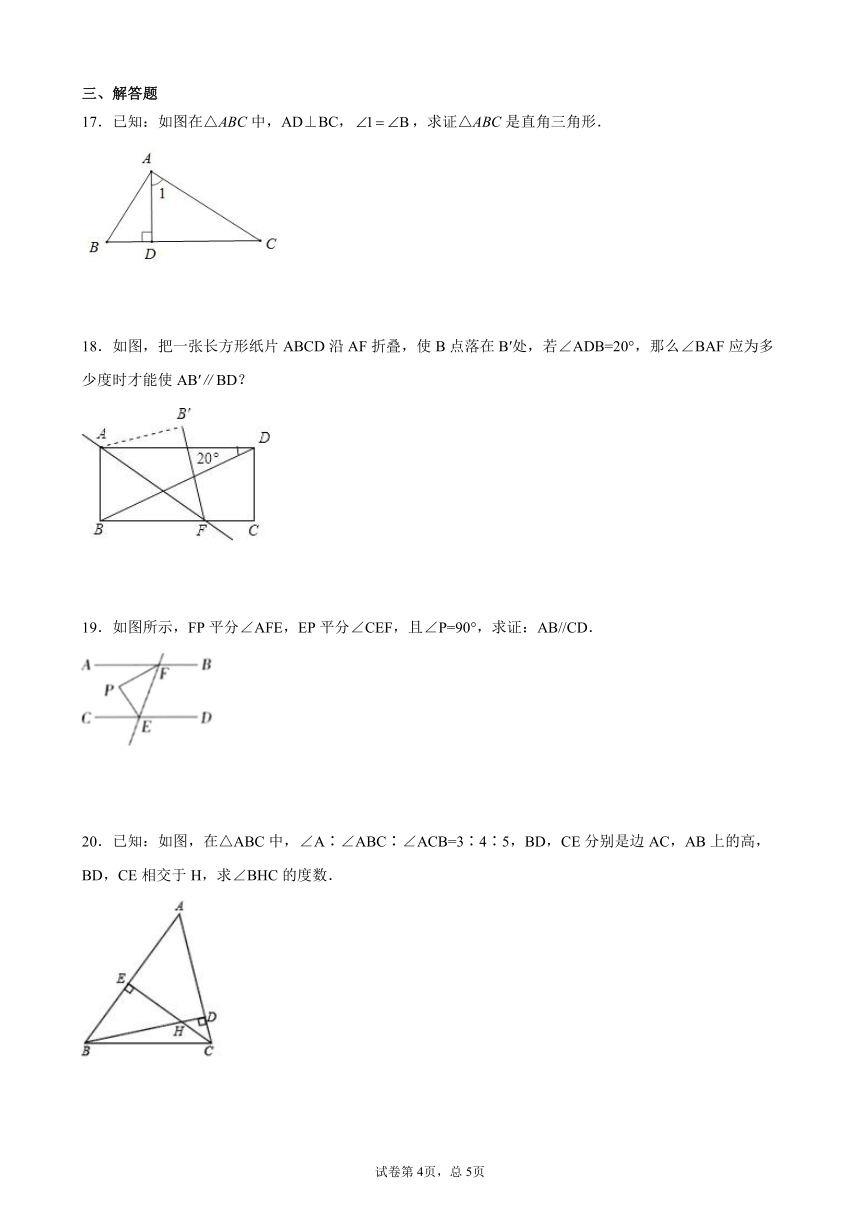
17.已知:如图在△ABC中,AD⊥BC,,求证△ABC是直角三角形.
18.如图,把一张长方形纸片ABCD沿AF折叠,使B点落在B′处,若∠ADB=20°,那么∠BAF应为多少度时才能使AB′∥BD?
19.如图所示,FP平分∠AFE,EP平分∠CEF,且∠P=90°,求证:AB//CD.
20.已知:如图,在△ABC中,∠A∶∠ABC∶∠ACB=3∶4∶5,BD,CE分别是边AC,AB上的高,BD,CE相交于H,求∠BHC的度数.
21.如图,在△ABC中,∠C=∠ABC=2∠A,BD是AC边上的高.求∠DBC的
度数.
22.如图,是A、B、C三个村庄的平面图,已知B村在A村的南偏西65°15′方向,C村在A村的南偏东15°方向,C村在B村的北偏东85°方向,求从C村观测A、B两村的视角∠ACB的度数.
23.如图,已知:在Rt△ABC中,∠C=90°,BD平分∠ABC且交AC于D.
(1)若∠BAC=30°,求证:AD=BD;
(2)若AP平分∠BAC且交BD于P,求∠BPA的度数
试卷第2页,总2页
参考答案
1.D
【解析】A、由和可得:∠C=90°,是直角三角形,此选项不符合题意;
B、由得,又,则∠A=90°,是直角三角形,此选项不符合题意;
C、由题意,,是直角三角形,此选项不符合题意;
D、由得3∠C+3∠C+∠C=180°,解得:,则∠A=∠B=≠90°,不是直角三角形,此选项符合题意,
故选:D.
2.B
【解析】设第一个内角的度数为x,∵三角形的一个内角是另一个内角的,是第三个内角的,∴另一个内角的度数为x,第三个内角为x,
∴x+x+x=180°,
解得x=48°,
∴三个内角分别为48°,72°,60°
故选B.
3.D
【解析】∵CD⊥BD,∠C=55°,
∴∠CBD=90°-55°=35°,
∵BD平分∠ABC,
∴∠ABC=2∠CBD=2×35°=70°,
故选D.
4.C
【解析】解:∵
∴∠FGB=∠ADB=90°,
∴FG∥AD,∠ADE+∠BDE=90°,
故①正确;
∵DE∥AC,
∴∠DEB=∠CAB=90°,
∴∠B+∠BDE=90°,
∴,
∴③正确;
∵,
∴∠BDE=∠C,
∵∠FGC=90°,
∴∠C+∠CFG=90°,
∴∠BDE+∠CFG=90°,
∴④正确;
∵∠ADB=90°,
∴∠ADE+∠BDE=90°,
∴②不正确;
故选:C.
5.D
【解析】∵△ABC中,∠ACB=90°,∠A=25°
∴∠B=90°-∠A=65°
由折叠的性质可得:∠CED=∠B=65°,∠BDC=∠EDC
∴∠ADE=∠CED-∠A=40°
∴∠BDC=(180°-∠ADE)=70°.
故选:D.
6.D
【解析】解:∵
∵,
,
由折叠的性质可知,
,
,
故选D.
7.B
【解析】解:AD平分∠BAC,∠BAD=30°,
∴∠BAC=60°,
∴∠C=180°﹣60°﹣40°=80°.
故选B.
8.A
【解析】如图所示,
∵EP⊥EF,
∴∠PEF=90°,
∵∠BEP=50°,
∴∠BEF=∠BEP+∠PEF=140°,
∵AB∥CD,
∴∠BEF+∠EFD=180°,
∴∠EFD=40°,
∵FP平分∠EFD,
∴∠EFP=∠EFD=20°,
∵∠PEF+∠EFP+∠EPF=180°,
∴∠EPF=70°.
故选A.
9.75
【解析】解:如图.
∵∠3=60°,∠4=45°,
∴∠1=180°-∠3-∠4=75°.
故答案为:75.
10.直角三角形
钝角三角形
角三角形或直角三角形或钝角三角形
【解析】解:,
当时,
∴2∠C=180°
∴,
∴为直角三角形;
当时,
∴,
∴为钝角三角形;
当时,
∴,
∴
当∠A,∠B时,是锐角三角形,
当∠A或∠B时,是直角三角形
当∠A或∠B时,是钝角三角形
则可能为锐角三角形或直角三角形或钝角三角形;
故答案为:直角三角形;钝角三角形;锐角三角形或直角三角形或钝角三角形.
11.
【解析】∵DE∥BC,
∴∠ADE=∠B=44°,
∵△ADE沿DE翻折,使得点A落在平面内的A′处,
∴∠A′DE=∠ADE=44°,
∴∠BDA′=180°?∠A′DE?∠ADE=180°?44°-44°=92°.
故答案是:92°.
12.50°
【解析】解:∠ADB:∠BDC=1:2,
设∠ADB=
x,
则∠BDC=2x.
AD
//BC,
∠DBC=∠ADB=
x,
∠C=30,∠C+∠DBC+∠BDC=180,即
30+x+2x=180,解得x=50
,
∠DBC=50.
故答案:50.
13.65°
25°
【解析】∵∠C=90°,
∴∠A+∠B=90°,
∵∠A-∠B=40°,
∴2∠A=130°,
∴∠A=65°,
∴∠B=90°-65°=25°.
故答案为:65°,25°.
14.10
【解析】解:∵∠B=50°,∠C=70°,
∴∠BAC=180°-∠B-∠C=180°-50°-70°=60°,
∵AD是角平分线,
∴∠BAD=∠BAC=×60°=30°,
∵AE是高,
∴∠BAE=90°-∠B=90°-50°=40°,
∴∠DAE=∠BAE-∠BAD=40°-30°=10°.
故答案为:10.
15.15
【解析】解:在△ABC中,
∵,,
∴∠ACB=60°.
在△DEF中,
∵∠EDF=90°,,
∴∠DEF=45°.
又∵∥,
∴∠CEF=∠ACB=60°,
∴∠CED=∠CEF-∠DEF=60°-45°=15°.
故答案为:15.
16.180°
【解析】∵∠ACD=∠A,∠BCF=∠B,∠DCF=∠ACD+∠ACB+∠BCF=180°,
∴∠A+∠B+∠ACB=∠ACD+∠ACB+∠BCF=180°.
故答案为180°.
17.证明见解析
【解析】∵AD⊥BC,
∴∠BAD+∠B=90°,
∵∠1=∠B,
∴∠1+∠BAD=∠BAC=90°,
∴△ABC是直角三角形.
18.55°.
【解析】解:∵长方形纸片ABCD沿AF折叠,使B点落在B′处,∴∠B′AF=∠BAF,
∵AB′∥BD,
∴∠B′AD=∠ADB=20°,
∴∠B′AB=20°+90°=110°,
∴∠BAF=110°÷2=55°.
∴∠BAF应为55度时才能使AB′∥BD.
19.详见解析
【解析】证明:∵∠P=90°(已知),
∴∠1+∠2=90°(三角形内角和定理).
∵PF平分,PE平分(已知),
∴
,(角平分线的定义).
∴(等量代换).
∴=180°(等式的性质).
∴AB//CD(同旁内角互补,两直线平行).
20.135°
【解析】解:∵在△ABC中,∠A:∠ABC:∠ACB=3:4:5,
故设∠A=3x,∠ABC=4x,∠ACB=5x.
∵在△ABC中,∠A+∠ABC+∠ACB=180°,
∴3x+4x+5x=180°,
解得x=15°,
∴∠A=3x=45°.
∵BD,CE分别是边AC,AB上的高,
∴∠ADB=90°,∠BEC=90°,
∴在△ABD中,∠ABD=180°-∠ADB-∠A=180°-90°-45°=45°,
∴∠BHC=∠ABD+∠BEC=45°+90°=135°.
21.18°
【解析】解:∵∠C=∠ABC=2∠A,
∴∠C+∠ABC+∠A=5∠A=180°,
∴∠A=36°.
则∠C=∠ABC=2∠A=72°.
又∵BD是AC边上的高,
∴∠BDC=90°,
则∠DBC=90°-∠C=18°.
22.80°
【解析】解:由题意得
∠BAE=65°15′,∠CAE=15°,∠DBC=85°,AE∥BD
∴∠BAC=∠BAE+∠CAE=65°15′+15°=80°15′,∠ABD=∠BAE=65°15′
∴∠ABC=∠DBC-∠ABD=85°﹣65°15′=19°45′.
在△ABC中,∠ACB=180°﹣∠BAC﹣∠ABC=180°﹣80°15′﹣19°45′
=80°.
23.(1)见解析
(2)135°
【解析】(1)证明:
又因为BD平分∠ABC,所以
(2)解:
答案第1页,总2页
答案第1页,总2页
11.2.1三角形的内角
时间:60分钟
一、单选题
1.具备下列条件的中,不是直角三角形的是(
)
A.
B.
C.
D.
2.已知三角形的一个内角是另一个内角的,是第三个内角的,则这个三角形各内角的度数分别为(
)
A.60°,90°,75°
B.48°,72°,60°
C.48°,32°,38°
D.40°,50°,90°
3.如图,BD平分∠ABC,CD⊥BD,D为垂足,∠C=55°,则∠ABC的度数是( )
A.35°
B.55°
C.60°
D.70°
4.如图,已知.则结论①;②平分;③;④.正确的是(
)
A.①②③
B.①②④
C.①③④
D.②③④
5.如图,△ABC中,∠ACB=90°,沿CD折叠△CBD,使点B恰好落在AC边上的点E处,若∠A=25°,则∠BDC等于( )
A.44°
B.60°
C.67°
D.70°
6.如图,将沿MN折叠,使,点A的对应点为点,若,,则的度数是(
)
A.
B.
C.
D.
7.如图,在△ABC中,AD平分∠BAC且与BC相交于点D,∠B=40°,∠BAD=30°,则∠C的度数是( )
A.70°
B.80°
C.100°
D.110°
8.如图,AB∥CD,EF与AB、CD分别相交于点E、F,EP⊥EF,与∠EFD的平分线FP相交于点P,且∠BEP=50°,则∠EPF=(
)度.
A.70
B.65
C.60
D.55
二、填空题
9.将一副直角三角板如图放置,使含30°角的三角板的短直角边和含45°角的三角板的一条直角边重合,则∠1的度数为_______度.
10.在中,若,则此三角形为__;若,则此三角形为___;若,则此三角形为___.(填“锐角三角形”、“钝角三角形”或“直角三角形”,可多选)
11.如图,△ABC中,
DE∥BC,将△ADE沿DE翻折,使得点A落在平面内的A′处,若∠B=44°,则∠BDA′的度数是__________.
12.如图,AD∥BC,∠C
=30°,
∠ADB:∠BDC=
1:2,则∠DBC的度数是_______.
13.在Rt△ABC中,,,那么________,___.
14.如图,AD、AE分别是△ABC的角平分线和高,∠B=50°,∠C=70°,则∠DAE=_____________°.
15.一副三角尺如图摆放,是延长线上一点,是上一点,,,,若∥,则等于_________度.
16.如图,∠ACD=∠A,∠BCF=∠B,则∠A+∠B+∠ACB等于______
.
三、解答题
17.已知:如图在△ABC中,AD⊥BC,,求证△ABC是直角三角形.
18.如图,把一张长方形纸片ABCD沿AF折叠,使B点落在B′处,若∠ADB=20°,那么∠BAF应为多少度时才能使AB′∥BD?
19.如图所示,FP平分∠AFE,EP平分∠CEF,且∠P=90°,求证:AB//CD.
20.已知:如图,在△ABC中,∠A∶∠ABC∶∠ACB=3∶4∶5,BD,CE分别是边AC,AB上的高,BD,CE相交于H,求∠BHC的度数.
21.如图,在△ABC中,∠C=∠ABC=2∠A,BD是AC边上的高.求∠DBC的
度数.
22.如图,是A、B、C三个村庄的平面图,已知B村在A村的南偏西65°15′方向,C村在A村的南偏东15°方向,C村在B村的北偏东85°方向,求从C村观测A、B两村的视角∠ACB的度数.
23.如图,已知:在Rt△ABC中,∠C=90°,BD平分∠ABC且交AC于D.
(1)若∠BAC=30°,求证:AD=BD;
(2)若AP平分∠BAC且交BD于P,求∠BPA的度数
试卷第2页,总2页
参考答案
1.D
【解析】A、由和可得:∠C=90°,是直角三角形,此选项不符合题意;
B、由得,又,则∠A=90°,是直角三角形,此选项不符合题意;
C、由题意,,是直角三角形,此选项不符合题意;
D、由得3∠C+3∠C+∠C=180°,解得:,则∠A=∠B=≠90°,不是直角三角形,此选项符合题意,
故选:D.
2.B
【解析】设第一个内角的度数为x,∵三角形的一个内角是另一个内角的,是第三个内角的,∴另一个内角的度数为x,第三个内角为x,
∴x+x+x=180°,
解得x=48°,
∴三个内角分别为48°,72°,60°
故选B.
3.D
【解析】∵CD⊥BD,∠C=55°,
∴∠CBD=90°-55°=35°,
∵BD平分∠ABC,
∴∠ABC=2∠CBD=2×35°=70°,
故选D.
4.C
【解析】解:∵
∴∠FGB=∠ADB=90°,
∴FG∥AD,∠ADE+∠BDE=90°,
故①正确;
∵DE∥AC,
∴∠DEB=∠CAB=90°,
∴∠B+∠BDE=90°,
∴,
∴③正确;
∵,
∴∠BDE=∠C,
∵∠FGC=90°,
∴∠C+∠CFG=90°,
∴∠BDE+∠CFG=90°,
∴④正确;
∵∠ADB=90°,
∴∠ADE+∠BDE=90°,
∴②不正确;
故选:C.
5.D
【解析】∵△ABC中,∠ACB=90°,∠A=25°
∴∠B=90°-∠A=65°
由折叠的性质可得:∠CED=∠B=65°,∠BDC=∠EDC
∴∠ADE=∠CED-∠A=40°
∴∠BDC=(180°-∠ADE)=70°.
故选:D.
6.D
【解析】解:∵
∵,
,
由折叠的性质可知,
,
,
故选D.
7.B
【解析】解:AD平分∠BAC,∠BAD=30°,
∴∠BAC=60°,
∴∠C=180°﹣60°﹣40°=80°.
故选B.
8.A
【解析】如图所示,
∵EP⊥EF,
∴∠PEF=90°,
∵∠BEP=50°,
∴∠BEF=∠BEP+∠PEF=140°,
∵AB∥CD,
∴∠BEF+∠EFD=180°,
∴∠EFD=40°,
∵FP平分∠EFD,
∴∠EFP=∠EFD=20°,
∵∠PEF+∠EFP+∠EPF=180°,
∴∠EPF=70°.
故选A.
9.75
【解析】解:如图.
∵∠3=60°,∠4=45°,
∴∠1=180°-∠3-∠4=75°.
故答案为:75.
10.直角三角形
钝角三角形
角三角形或直角三角形或钝角三角形
【解析】解:,
当时,
∴2∠C=180°
∴,
∴为直角三角形;
当时,
∴,
∴为钝角三角形;
当时,
∴,
∴
当∠A,∠B时,是锐角三角形,
当∠A或∠B时,是直角三角形
当∠A或∠B时,是钝角三角形
则可能为锐角三角形或直角三角形或钝角三角形;
故答案为:直角三角形;钝角三角形;锐角三角形或直角三角形或钝角三角形.
11.
【解析】∵DE∥BC,
∴∠ADE=∠B=44°,
∵△ADE沿DE翻折,使得点A落在平面内的A′处,
∴∠A′DE=∠ADE=44°,
∴∠BDA′=180°?∠A′DE?∠ADE=180°?44°-44°=92°.
故答案是:92°.
12.50°
【解析】解:∠ADB:∠BDC=1:2,
设∠ADB=
x,
则∠BDC=2x.
AD
//BC,
∠DBC=∠ADB=
x,
∠C=30,∠C+∠DBC+∠BDC=180,即
30+x+2x=180,解得x=50
,
∠DBC=50.
故答案:50.
13.65°
25°
【解析】∵∠C=90°,
∴∠A+∠B=90°,
∵∠A-∠B=40°,
∴2∠A=130°,
∴∠A=65°,
∴∠B=90°-65°=25°.
故答案为:65°,25°.
14.10
【解析】解:∵∠B=50°,∠C=70°,
∴∠BAC=180°-∠B-∠C=180°-50°-70°=60°,
∵AD是角平分线,
∴∠BAD=∠BAC=×60°=30°,
∵AE是高,
∴∠BAE=90°-∠B=90°-50°=40°,
∴∠DAE=∠BAE-∠BAD=40°-30°=10°.
故答案为:10.
15.15
【解析】解:在△ABC中,
∵,,
∴∠ACB=60°.
在△DEF中,
∵∠EDF=90°,,
∴∠DEF=45°.
又∵∥,
∴∠CEF=∠ACB=60°,
∴∠CED=∠CEF-∠DEF=60°-45°=15°.
故答案为:15.
16.180°
【解析】∵∠ACD=∠A,∠BCF=∠B,∠DCF=∠ACD+∠ACB+∠BCF=180°,
∴∠A+∠B+∠ACB=∠ACD+∠ACB+∠BCF=180°.
故答案为180°.
17.证明见解析
【解析】∵AD⊥BC,
∴∠BAD+∠B=90°,
∵∠1=∠B,
∴∠1+∠BAD=∠BAC=90°,
∴△ABC是直角三角形.
18.55°.
【解析】解:∵长方形纸片ABCD沿AF折叠,使B点落在B′处,∴∠B′AF=∠BAF,
∵AB′∥BD,
∴∠B′AD=∠ADB=20°,
∴∠B′AB=20°+90°=110°,
∴∠BAF=110°÷2=55°.
∴∠BAF应为55度时才能使AB′∥BD.
19.详见解析
【解析】证明:∵∠P=90°(已知),
∴∠1+∠2=90°(三角形内角和定理).
∵PF平分,PE平分(已知),
∴
,(角平分线的定义).
∴(等量代换).
∴=180°(等式的性质).
∴AB//CD(同旁内角互补,两直线平行).
20.135°
【解析】解:∵在△ABC中,∠A:∠ABC:∠ACB=3:4:5,
故设∠A=3x,∠ABC=4x,∠ACB=5x.
∵在△ABC中,∠A+∠ABC+∠ACB=180°,
∴3x+4x+5x=180°,
解得x=15°,
∴∠A=3x=45°.
∵BD,CE分别是边AC,AB上的高,
∴∠ADB=90°,∠BEC=90°,
∴在△ABD中,∠ABD=180°-∠ADB-∠A=180°-90°-45°=45°,
∴∠BHC=∠ABD+∠BEC=45°+90°=135°.
21.18°
【解析】解:∵∠C=∠ABC=2∠A,
∴∠C+∠ABC+∠A=5∠A=180°,
∴∠A=36°.
则∠C=∠ABC=2∠A=72°.
又∵BD是AC边上的高,
∴∠BDC=90°,
则∠DBC=90°-∠C=18°.
22.80°
【解析】解:由题意得
∠BAE=65°15′,∠CAE=15°,∠DBC=85°,AE∥BD
∴∠BAC=∠BAE+∠CAE=65°15′+15°=80°15′,∠ABD=∠BAE=65°15′
∴∠ABC=∠DBC-∠ABD=85°﹣65°15′=19°45′.
在△ABC中,∠ACB=180°﹣∠BAC﹣∠ABC=180°﹣80°15′﹣19°45′
=80°.
23.(1)见解析
(2)135°
【解析】(1)证明:
又因为BD平分∠ABC,所以
(2)解:
答案第1页,总2页
答案第1页,总2页
