12.2三角形全等的判定(二)课堂同步习题 2021-2022学年八年级数学人教版上册(Word版 含答案)
文档属性
| 名称 | 12.2三角形全等的判定(二)课堂同步习题 2021-2022学年八年级数学人教版上册(Word版 含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 486.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-07 09:35:23 | ||
图片预览




文档简介
2021-2022学年初中数学八年级上册课堂同步(人教版)
12.2三角形全等的判定
时间:60分钟;
一、单选题
1.课本上运用尺规作图:作一个角等于已知角,其作图的依据是(
)
A.
B.
C.
D.
2.如图,乐乐书上的三角形墨迹污染了一部分,很快他就画出一个三角形与书上的三角形全等,这两个三角形全等的依据是(
)
A.
B.
C.
D.
3.如图,两根长度为12米的绳子,一端系在旗杆上,另一端分别固定在地面两个木桩上,则两个木桩离旗杆底部的距离与的距离间的关系是(
)
A.
B.
C.
D.不能确定
4.如图,已知,,添加下列条件仍不能判定的是(
)
A.
B.
C.
D.
5.如图,要测量河两岸相对的两点A,B的距离,先在的垂线上取两点C,D,使,再作出的垂线,使A,C,E在一条直线上,可以说明,得,因此测得的长就是的长,判定最恰当的理由是(
)
A.边角边
B.角角边
C.边边边
D.角边角
6.如图,BE=CF,AE⊥BC,DF⊥BC,要根据“HL”证明Rt△ABE≌Rt△DCF,则还需要添加一个条件是( )
A.AE=DF
B.∠A=∠D
C.∠B=∠C
D.AB=
CD
7.下列条件不能判定两个直角三角形全等的是(
)
A.两条直角边对应相等
B.斜边和一锐角对应相等
C.斜边和一直角边对应相等
D.两个锐角对应相等
8.如图,在中,,,垂足分别是D,E,AD,CE交于点H.已知,,则CH的长为(
)
A.1
B.2
C.
D.
二、填空题
9.如图,要测量水池宽,可从点出发在地面上画一条线段,使,再从点观测,在的延长线上测得一点,使,这时量得,则水池宽的长度是__m.
10.已知,如图,AB∥CD,AF∥DE,AF=DE,且BE=2,BC=10,则EF=________.
11.如图,小明把一块三角形的玻璃片打碎成三块,现要到玻璃店去配一块完全相同的玻璃片,那么最省事的办法是带________去.
12.如图,AC⊥BC,AD⊥BD,垂足分别是C、D,若要用“HL”得到Rt△ABC≌Rt△BAD,则你添加的条件是______________.(写一种即可)
13.补充一个条件,使推理完整,
在和中,
,____,,
14.如图,用直尺和圆规作一个角等于已知角,能得出的依据是__.
15.用尺规作一个直角三角形,使其两直角边分别等于已知线段,则作图的依据是________
.
16.如图,已知PA⊥ON于A,PB⊥OM于B,且PA=PB,∠MON=50°,∠OPC=30°,则∠PCA=________.
三、解答题
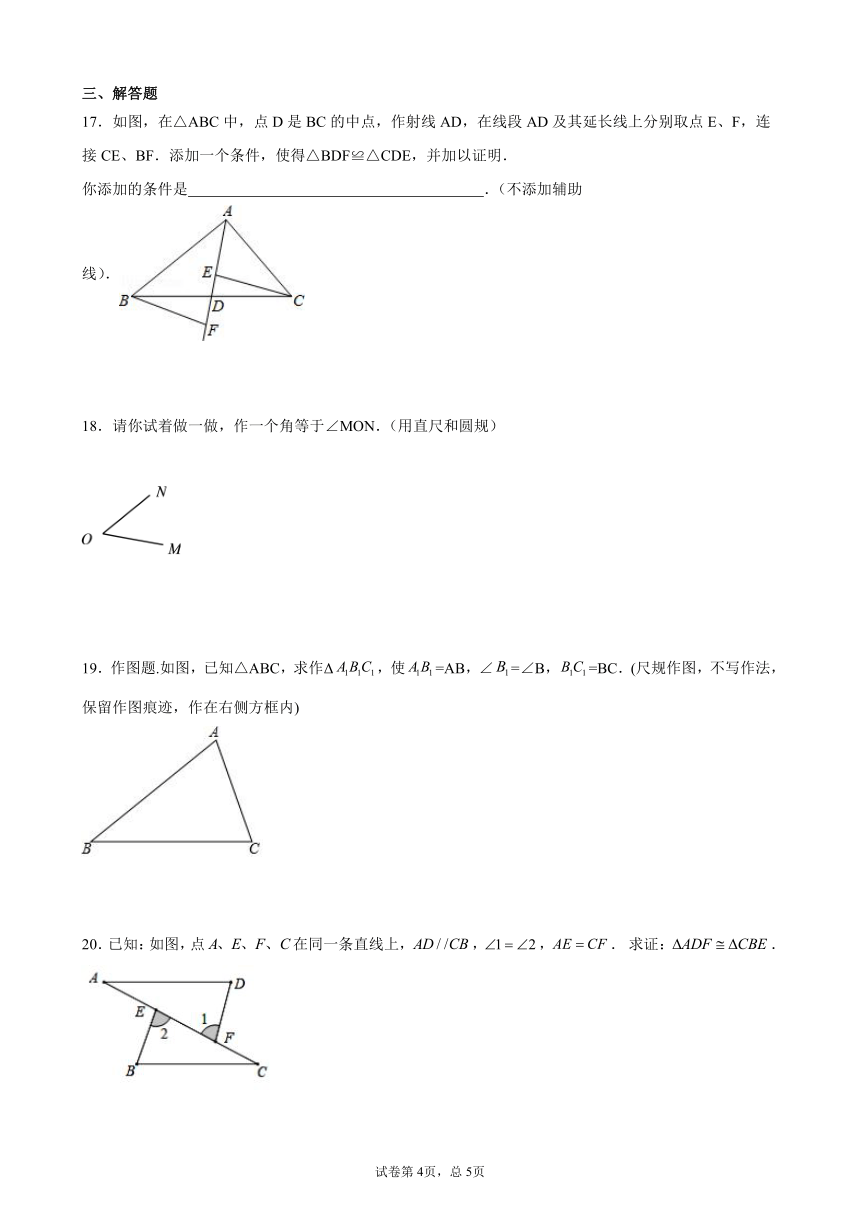
17.如图,在△ABC中,点D是BC的中点,作射线AD,在线段AD及其延长线上分别取点E、F,连接CE、BF.添加一个条件,使得△BDF≌△CDE,并加以证明.
你添加的条件是
.(不添加辅助线).
18.请你试着做一做,作一个角等于∠MON.(用直尺和圆规)
19.作图题.如图,已知△ABC,求作Δ,使=AB,∠=∠B,=BC.(尺规作图,不写作法,保留作图痕迹,作在右侧方框内)
20.已知:如图,点在同一条直线上,,,.
求证:.
21.如图,在中,,点D,E分别为上的点,,若,求证:.
22.如图,已知AD,AF分别是钝角和钝角的高,如果.求证:.
23.如图所示,有两个长度相同的滑梯和,,,垂足分别为,,左边滑梯的高度与右边滑梯水平方向的长度相等.问:两个滑梯的倾斜角和的大小有什么关系?
24.已知:点O到△ABC的两边AB,AC所在直线的距离相等,且OB=OC.
(1)如图①,若点O在BC上,求证:∠B=∠C;
(2)如图②,若点O在△ABC的内部,求证:∠ABO=∠ACO.
试卷第2页,总2页
参考答案
1.A
【解析】解:在尺规作图中,作一个角等于已知角是通过构建三边对应相等的全等三角形来证,因此由作法知其判定依据是SSS,即边边边公理.
故选:A.
2.B
【解析】解:根据题意,三角形的两角和他们的夹边是完整的,所以可以利用“角边角”定理作出完全一样的三角形
故选:B
3.C
【解析】解:,
,
由,,
,
.
故选:C.
4.B
【解析】A、若,可用“角边角”证明,故A不符合题意;
B、若,是“边边角”不能证明,故B符合题意;
C、若,可用“边角边”证明,故C不符合题意;
D、若,可得,则可用“角角边”证明,故D不符合题意;
故选:B.
5.D
【解析】证明:∵,,
∴∠ABC=∠EDC=90°,
在和中,
,
∴(角边角),
故选:D.
6.D
【解析】添加的条件是AB=CD;理由如下:
∵AE⊥BC,DF⊥BC,
∴∠CFD=∠AEB=90°,
在Rt△ABE和Rt△DCF中,
,
∴
(HL).
故选:D.
7.D
【解析】解:、可以利用边角边判定两三角形全等,故本选项不合题意;
、可以利用角角边判定两三角形全等,故本选项不合题意;
、根据斜边直角边定理判定两三角形全等,故本选项不合题意;
、三个角对应相等不能证明两三角形全等,故本选项符合题意;
故选:D.
8.B
【解析】∵AD⊥BC,CE⊥AB,
∴∠BEC=∠ADB=90°,
∵∠BAD+∠B=90°,∠BCE+∠B=90°,
∴∠BAD=∠BCE,
在△BCE和△HAE中,
,
∴△BCE≌△HAE(AAS),
∴CE=AE=6,
∴CH=CE-HE=6-4=2.
故选:B.
9.120
【解析】,
,
,,
,
,
故答案为120.
10.6
【解析】∵AB∥CD,AF∥DE,
∴∠B=∠C,∠AFB=∠DEC,
在△ABF和△CDE中
,
∴△ABF≌△DCE(AAS),
∴BF=CE,
∴BF?EF=CE?EF,
即CF=EB=2,
∵BC=10,
∴EF=10?2?2=6,
故答案为6.
11.③
【解析】第①块只保留了原三角形的一个角和部分边,第②块只保留了原三角形的部分边,根据这两块中的任何一块均不能配一块与原来完全相同的玻璃片;第③块不仅保留了原来三角形的两个角还保留了一边,则可以根据“ASA”来配一块完全相同的玻璃片.
12.AC=BD或AD=BC.(答案不唯一)
【解析】AC=BD或AD=BC都可以.
13.
【解析】解:补充:,理由如下:
在和中,
,,,
.
故答案为:
14.
【解析】在和△中,
,
△,
故答案为:.
15.SAS
【解析】解::用尺规做直角三角形,已知两直角边.可以先画出两条已知线段和确定一个直角,作图的依据为SAS.
16.55°
【解析】解:∵PA⊥ON于A,PB⊥OM于B,
∴∠PAO=∠PBO=90°,
∵PA=PB,OP=OP,
∴Rt△OAP≌Rt△OBP(HL),
∴∠AOP=∠BOP=∠AOB=25°,
∴∠PCA=∠AOP+∠OPC=55°,
故答案为:55°.
17.答案不唯一
【解析】(1)添加的条件是:DE=DF(或CE∥BF或∠ECD=∠DBF或∠DEC=∠DFB等).
(2)证明:在△BDF和△CDE中
∵
∴△BDF≌△CDE.
18.作图见解析
【解析】作法:①作射线O′A′;
②以点O为圆心,以任意长为半径作弧,交OM于C,交ON于D.?
③以点O′为圆心,以OC长为半径作弧,交O′A′于C′.?
④以点C′为圆心,以CD为半径作弧,交前弧于D′.
⑤经过点D′作射线O′B′,∠A′O′B′就是所求的角.?
19.见解析
【解析】解:如图所示,Δ即为所求.
20.见解析
【解析】解:,,
,
即,
在和中:,
.
21.详见解析
【解析】证明:,,
.
,
.
在和中,
,
.
22.证明见解析.
【解析】解:∵,AF分别是钝角和钝角的高,
.
,,
.
23.,理由见解析
【解析】解:;理由如下:
由题意可得:与均是直角三角形,且,.
在和中,
,
,
,
,
.
24.(1)详见解析;(2)详见解析
【解析】在Rt△OEC和Rt△OFB中,∵,
∴Rt△OEC≌Rt△OFB(H.L.),∴∠B=∠C(全等三角形的对应角相等)
(2)在Rt△OEC和Rt△OFB中,∵,
∴Rt△OEC≌Rt△OFB(H.L.),∴∠ABO=∠ACO
答案第1页,总2页
答案第1页,总2页
12.2三角形全等的判定
时间:60分钟;
一、单选题
1.课本上运用尺规作图:作一个角等于已知角,其作图的依据是(
)
A.
B.
C.
D.
2.如图,乐乐书上的三角形墨迹污染了一部分,很快他就画出一个三角形与书上的三角形全等,这两个三角形全等的依据是(
)
A.
B.
C.
D.
3.如图,两根长度为12米的绳子,一端系在旗杆上,另一端分别固定在地面两个木桩上,则两个木桩离旗杆底部的距离与的距离间的关系是(
)
A.
B.
C.
D.不能确定
4.如图,已知,,添加下列条件仍不能判定的是(
)
A.
B.
C.
D.
5.如图,要测量河两岸相对的两点A,B的距离,先在的垂线上取两点C,D,使,再作出的垂线,使A,C,E在一条直线上,可以说明,得,因此测得的长就是的长,判定最恰当的理由是(
)
A.边角边
B.角角边
C.边边边
D.角边角
6.如图,BE=CF,AE⊥BC,DF⊥BC,要根据“HL”证明Rt△ABE≌Rt△DCF,则还需要添加一个条件是( )
A.AE=DF
B.∠A=∠D
C.∠B=∠C
D.AB=
CD
7.下列条件不能判定两个直角三角形全等的是(
)
A.两条直角边对应相等
B.斜边和一锐角对应相等
C.斜边和一直角边对应相等
D.两个锐角对应相等
8.如图,在中,,,垂足分别是D,E,AD,CE交于点H.已知,,则CH的长为(
)
A.1
B.2
C.
D.
二、填空题
9.如图,要测量水池宽,可从点出发在地面上画一条线段,使,再从点观测,在的延长线上测得一点,使,这时量得,则水池宽的长度是__m.
10.已知,如图,AB∥CD,AF∥DE,AF=DE,且BE=2,BC=10,则EF=________.
11.如图,小明把一块三角形的玻璃片打碎成三块,现要到玻璃店去配一块完全相同的玻璃片,那么最省事的办法是带________去.
12.如图,AC⊥BC,AD⊥BD,垂足分别是C、D,若要用“HL”得到Rt△ABC≌Rt△BAD,则你添加的条件是______________.(写一种即可)
13.补充一个条件,使推理完整,
在和中,
,____,,
14.如图,用直尺和圆规作一个角等于已知角,能得出的依据是__.
15.用尺规作一个直角三角形,使其两直角边分别等于已知线段,则作图的依据是________
.
16.如图,已知PA⊥ON于A,PB⊥OM于B,且PA=PB,∠MON=50°,∠OPC=30°,则∠PCA=________.
三、解答题
17.如图,在△ABC中,点D是BC的中点,作射线AD,在线段AD及其延长线上分别取点E、F,连接CE、BF.添加一个条件,使得△BDF≌△CDE,并加以证明.
你添加的条件是
.(不添加辅助线).
18.请你试着做一做,作一个角等于∠MON.(用直尺和圆规)
19.作图题.如图,已知△ABC,求作Δ,使=AB,∠=∠B,=BC.(尺规作图,不写作法,保留作图痕迹,作在右侧方框内)
20.已知:如图,点在同一条直线上,,,.
求证:.
21.如图,在中,,点D,E分别为上的点,,若,求证:.
22.如图,已知AD,AF分别是钝角和钝角的高,如果.求证:.
23.如图所示,有两个长度相同的滑梯和,,,垂足分别为,,左边滑梯的高度与右边滑梯水平方向的长度相等.问:两个滑梯的倾斜角和的大小有什么关系?
24.已知:点O到△ABC的两边AB,AC所在直线的距离相等,且OB=OC.
(1)如图①,若点O在BC上,求证:∠B=∠C;
(2)如图②,若点O在△ABC的内部,求证:∠ABO=∠ACO.
试卷第2页,总2页
参考答案
1.A
【解析】解:在尺规作图中,作一个角等于已知角是通过构建三边对应相等的全等三角形来证,因此由作法知其判定依据是SSS,即边边边公理.
故选:A.
2.B
【解析】解:根据题意,三角形的两角和他们的夹边是完整的,所以可以利用“角边角”定理作出完全一样的三角形
故选:B
3.C
【解析】解:,
,
由,,
,
.
故选:C.
4.B
【解析】A、若,可用“角边角”证明,故A不符合题意;
B、若,是“边边角”不能证明,故B符合题意;
C、若,可用“边角边”证明,故C不符合题意;
D、若,可得,则可用“角角边”证明,故D不符合题意;
故选:B.
5.D
【解析】证明:∵,,
∴∠ABC=∠EDC=90°,
在和中,
,
∴(角边角),
故选:D.
6.D
【解析】添加的条件是AB=CD;理由如下:
∵AE⊥BC,DF⊥BC,
∴∠CFD=∠AEB=90°,
在Rt△ABE和Rt△DCF中,
,
∴
(HL).
故选:D.
7.D
【解析】解:、可以利用边角边判定两三角形全等,故本选项不合题意;
、可以利用角角边判定两三角形全等,故本选项不合题意;
、根据斜边直角边定理判定两三角形全等,故本选项不合题意;
、三个角对应相等不能证明两三角形全等,故本选项符合题意;
故选:D.
8.B
【解析】∵AD⊥BC,CE⊥AB,
∴∠BEC=∠ADB=90°,
∵∠BAD+∠B=90°,∠BCE+∠B=90°,
∴∠BAD=∠BCE,
在△BCE和△HAE中,
,
∴△BCE≌△HAE(AAS),
∴CE=AE=6,
∴CH=CE-HE=6-4=2.
故选:B.
9.120
【解析】,
,
,,
,
,
故答案为120.
10.6
【解析】∵AB∥CD,AF∥DE,
∴∠B=∠C,∠AFB=∠DEC,
在△ABF和△CDE中
,
∴△ABF≌△DCE(AAS),
∴BF=CE,
∴BF?EF=CE?EF,
即CF=EB=2,
∵BC=10,
∴EF=10?2?2=6,
故答案为6.
11.③
【解析】第①块只保留了原三角形的一个角和部分边,第②块只保留了原三角形的部分边,根据这两块中的任何一块均不能配一块与原来完全相同的玻璃片;第③块不仅保留了原来三角形的两个角还保留了一边,则可以根据“ASA”来配一块完全相同的玻璃片.
12.AC=BD或AD=BC.(答案不唯一)
【解析】AC=BD或AD=BC都可以.
13.
【解析】解:补充:,理由如下:
在和中,
,,,
.
故答案为:
14.
【解析】在和△中,
,
△,
故答案为:.
15.SAS
【解析】解::用尺规做直角三角形,已知两直角边.可以先画出两条已知线段和确定一个直角,作图的依据为SAS.
16.55°
【解析】解:∵PA⊥ON于A,PB⊥OM于B,
∴∠PAO=∠PBO=90°,
∵PA=PB,OP=OP,
∴Rt△OAP≌Rt△OBP(HL),
∴∠AOP=∠BOP=∠AOB=25°,
∴∠PCA=∠AOP+∠OPC=55°,
故答案为:55°.
17.答案不唯一
【解析】(1)添加的条件是:DE=DF(或CE∥BF或∠ECD=∠DBF或∠DEC=∠DFB等).
(2)证明:在△BDF和△CDE中
∵
∴△BDF≌△CDE.
18.作图见解析
【解析】作法:①作射线O′A′;
②以点O为圆心,以任意长为半径作弧,交OM于C,交ON于D.?
③以点O′为圆心,以OC长为半径作弧,交O′A′于C′.?
④以点C′为圆心,以CD为半径作弧,交前弧于D′.
⑤经过点D′作射线O′B′,∠A′O′B′就是所求的角.?
19.见解析
【解析】解:如图所示,Δ即为所求.
20.见解析
【解析】解:,,
,
即,
在和中:,
.
21.详见解析
【解析】证明:,,
.
,
.
在和中,
,
.
22.证明见解析.
【解析】解:∵,AF分别是钝角和钝角的高,
.
,,
.
23.,理由见解析
【解析】解:;理由如下:
由题意可得:与均是直角三角形,且,.
在和中,
,
,
,
,
.
24.(1)详见解析;(2)详见解析
【解析】在Rt△OEC和Rt△OFB中,∵,
∴Rt△OEC≌Rt△OFB(H.L.),∴∠B=∠C(全等三角形的对应角相等)
(2)在Rt△OEC和Rt△OFB中,∵,
∴Rt△OEC≌Rt△OFB(H.L.),∴∠ABO=∠ACO
答案第1页,总2页
答案第1页,总2页
