12.2三角形全等的判定课堂同步习题 2021-2022学年八年级数学人教版上册(Word版 含答案)
文档属性
| 名称 | 12.2三角形全等的判定课堂同步习题 2021-2022学年八年级数学人教版上册(Word版 含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 681.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-07 09:37:13 | ||
图片预览



文档简介
2021-2022学年初中数学八年级上册课堂同步(人教版)
12.2三角形全等的判定
时间:60分钟;
一、单选题
1.下列三角形中,能全等的是(
)
(1)一腰和顶角对应相等的两个等腰三角形;
(2)一腰和一个角分别相等的两个等腰三角形;
(3)有两边分别相等的两个直角三角形;
(4)两条直角边对应相等的两个直角三角形.
A.(1)(3)
B.(2)(4)
C.(1)(4)
D.(1)(3)(4)
2.用直尺和圆规作一个角等于已知角,如图,能得出的依据是(
)
A.
B.
C.
D.
3.如图,在△ABC中,AB=8,AC=6,AD是BC边上的中线,则AD长的取值范围是(
)
A.6B.2C.1D.无法确定
4.已知如图,AD∥BC,AB⊥BC,CD⊥DE,CD=ED,AD=2,BC=3,则△ADE的面积为( )
A.1
B.2
C.5
D.无法确定
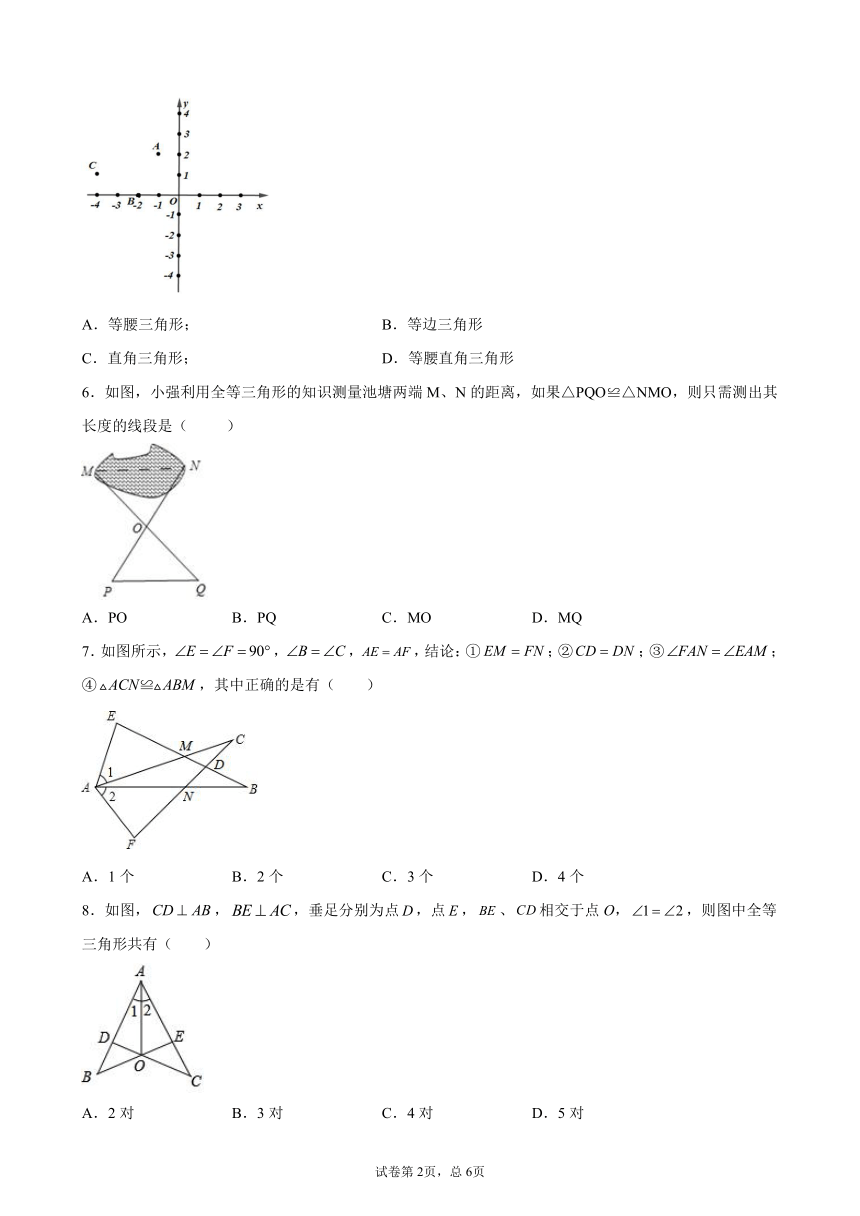
5.如图,△ABC是一个什么三角形?(
)请说明理由.
A.等腰三角形;
B.等边三角形
C.直角三角形;
D.等腰直角三角形
6.如图,小强利用全等三角形的知识测量池塘两端M、N的距离,如果△PQO≌△NMO,则只需测出其长度的线段是(
)
A.PO
B.PQ
C.MO
D.MQ
7.如图所示,,,,结论:①;②;③;④,其中正确的是有(
)
A.1个
B.2个
C.3个
D.4个
8.如图,,,垂足分别为点,点,、相交于点O,,则图中全等三角形共有(
)
A.2对
B.3对
C.4对
D.5对
二、填空题
9.如图,已知△ABC的六个元素,其中a、b、c表示三角形三边的长,则下面甲、乙、丙三个三角形中和△ABC一定全等的图形是__.
10.如图,△ABC是不等边三角形,DE=BC,以D,E为两个顶点作位置不同的三角形,使所作的三角形与△ABC全等,这样的三角形最多可以画出______个.
11.如图所示,等腰直角三角形中,,,为的中点,.则四边形的面积为______.
12.如图,方格纸上有一个格点三角形和一条格点线段AB,在这个格点纸上找一点C,使得△ABC与这个格点三角形全等,这样的C点可以找到________个.
13.如图,在等边三角形ABC中,BD=CE,AD,BE交于点F,则_________;
14.在ABC中,AB=3,AC=4,则BC边上的中线AD的取值范围是_________
15.如图已知:AD平分∠BAC,AC=AB+BD,∠B=56°,求∠C=_____
16.如图,已知,,,则等于________.
三、解答题
17.如图,在中,是的中点,,,垂足分别是点、,.
(1)图中有几对全等的三角形?请一一列出;
(2)选择一对你认为全等的三角形进行证明.
18.如图,,,。求证:。
19.如图所示,要测量一个沼泽水潭的宽度.现由于不能直接测量,小军是这样操作的:他在平地上选取一点C,该点可以直接到达A与B点,接着他量出AC和BC的距离,并找出AC与BC的中点E、F,连接EF,测量EF的长,于是他便知道了水潭AB的长等于2EF,小军的做法有道理吗?说明理由.你还有比小军更简单的方法吗?
20.如图,在等边中,点是边上一点,连接,将线段绕点按顺时针方向旋转后得到,连接.求证:.
21.如图,在中,,,是上的一点,且的延长线交于,又平分,求证:.
22.如图所示,AD平分∠BAC,P是射线AD上一点,P与A不重合,.
求证:.
23.如图,CD⊥AB于点D,BE⊥AC于点E,△ABE≌△ACD,∠C=42°,AB=9,AD=6,G为AB延长线上一点.
(1)求∠EBG的度数.
(2)求CE的长.
24.已知,,,.直线过点,交、于点、.
(1)若是中线,求证:;
(2)若,求证:.
试卷第2页,总2页
参考答案
1.C
【解析】解:(1)两个等腰三角形的顶角相等,则两个底角也对应相等,所以一腰和顶角对应相等的两个等腰三角形全等,故符合题意;
(2)当一个三角形的底角和另一个三角形的顶角相等时,就不能推出两三角形全等,故本选项不符合题意;
(3)当一个三角形的斜边和另一个三角形的直角边相等,
如图,,但是两三角形不全等,
故本选项不符合题意;
(4)符合公理,能推出两直角三角形全等,故本选项符合题意;
故选:.
2.B
【解析】解:作图的步骤:
①以O为圆心,任意长为半径画弧,分别交OA、OB于点D、C;
②任意作一点O′,作射线O′B′,以O′为圆心,OC长为半径画弧,交O′B′于点C′;
③以C′为圆心,CD长为半径画弧,交前弧于点D′;
④过点D′作射线O′A′.
所以∠A′O′B′就是与∠AOB相等的角;
作图完毕.
在△OCD与△O′C′D′,
,
∴△OCD≌△O′C′D′(SSS),
∴∠A′O′B′=∠AOB,
显然运用的判定方法是SSS.
故选:B.
3.C
【解析】解:延长AD到E,使AD=DE,连接BE,如图所示:
∵AD=DE,∠ADC=∠BDE,BD=DC,
∴△ADC≌△EDB(SAS)
∴BE=AC=6,
在△AEB中,AB-BE<AE<AB+BE,
即8-6<2AD<8+6,
∴1<AD<7,
故选:C.
4.A
【解析】过D作BC的垂线交BC于G,过E作AD的垂线交AD的延长线于F,
∵∠EDF+∠FDC=90°,
∠GDC+∠FDC=90°,
∴∠EDF=∠GDC,
于是在Rt△EDF和Rt△CDG中,
,
∴△DEF≌△DCG,
∴EF=CG=BC﹣BG=BC﹣AD=3﹣2=1,
所以,S△ADE=(AD×EF)÷2=(2×1)÷2=1.
故选A.
5.D
【解析】如图,由题意知:AE=BD=2,CD=BE=1,∠AEB=∠BDC=90°,
在和中:
∴,
∴∠ABE=∠BCD,AB=BC,
又∵∠BCD+∠CBD=90°,
∴∠ABE+∠CBD=90°,
∴为等腰直角三角形,
故答案为:D.
6.B
【解析】解:要想利用△PQO≌△NMO求得MN的长,只需求得线段PQ的长,故选B.
7.C
【解析】解:∵,
∴△AEB≌△AFC;(AAS)
∴∠FAM=∠EAN,
∴∠EAN-∠MAN=∠FAM-∠MAN,即∠EAM=∠FAN;(故③正确)
又∵∠E=∠F=90°,AE=AF,
∴△EAM≌△FAN;(ASA)
∴EM=FN;(故①正确)
由△AEB≌△AFC知:∠B=∠C,AC=AB;
又∵∠CAB=∠BAC,
∴△ACN≌△ABM;(故④正确)
由于条件不足,无法证得②CD=DN;故正确的结论有:①③④;
故选:C.
8.C
【解析】解:∵CD⊥AB,BE⊥AC,
∴∠ADO=∠AEO=90°,
又∵∠1=∠2,AO=AO,
∴ADO≌AEO;(AAS)
∴OD=OE,AD=AE,
∵∠DOB=∠EOC,∠ODB=∠OEC=90°,OD=OE,
∴BOD≌COE;(ASA)
∴BD=CE,OB=OC,∠B=∠C,
∵AE=AD,∠DAC=∠CAB,∠ADC=∠AEB=90°
∴ADC≌AEB;(ASA)
∵AD=AE,BD=CE,
∴AB=AC,
∵OB=OC,AO=AO,
∴ABO≌ACO.(SSS)
所以共有四对全等三角形.
故选:C.
9.乙和丙
【解析】解:由SAS可知,图乙与△ABC全等,
由AAS可知,图丙与△ABC全等,
故答案为:乙和丙.
10.4
【解析】如图,能画4个,分别是:以D为圆心,AB为半径画圆;以C为圆心,CA为半径画圆.两圆相交于两点(DE上下各一个),分别于D、E连接后,可得到两个三角形;以D为圆心,AC为半径画圆;以E为圆心,AB为半径画圆.两圆相交于两点(DE上下各一个),分别于D、E连接后,可得到两个三角形.因此最多能画出4个
11.
【解析】(1)连接BO.
∵是等腰三角形,,,
∴,
又∵O是AC中点,
∴BO⊥AC,∠ABO=∠CBO=∠A=∠C=45°,BO=AO=CO=,
∵∠EOB+∠FOB=90°,∠FOB+∠COF=90°,
∴∠EOB=∠COF,
在△BEO和△CFO中,
,
∴,
∴.
12.4个
【解析】根据三边相等可得:有4个三角形可以和已知三角形全等.
13.60°
【解析】解:在等边△ABC中,AB=BC,∠ABC=∠C=60°,
在△ABD和△BCE中,
∵,
∴△ABD≌△BCE(SAS),
∴∠BAD=∠CBE,
在△ABF中,∠AFE=∠BAD+∠ABF=∠CBE+∠ABF=∠ABC=60°,
即∠AFE=60°.
故答案为:60°.
14.0.5<AD<3.5.
【解析】解:如图,延长AD到E,使DE=AD,
∵AD是BC边上的中线,
∴BD=CD,
在△ABD和△ECD中
,
∴△ABD≌△ECD(SAS),
∴CE=AB,
∵AB=3,AC=4,
∴4-3<AE<4+3,
即1<AE<7,
∴0.5<AD<3.5.
故答案为:0.5<AD<3.5.
15.31°.
【解析】如图,在AC上截取AE=AB,连接DE,
∵AD平分∠BAC,
∴∠BAD=∠EAD,
而AD是公共边,
∴△ABD≌△ADE,
∴∠B=∠AED=62°,DE=BD,
而AB+BD=AC=AE+CE,
∴DE=CE,
∴∠EDC=∠C,
而∠AED=∠C+∠EDC=62°,
∴∠C=31°.
16.
【解析】在和中,
∵,
,
,
,
故答案为40°.
17.(1)3对;分别是:≌.≌.≌;(2)见解析.
【解析】(1)解:3对.分别是:≌,≌,≌;
(2)以≌为例证明.
∵,,
∴.
又是的中点,
∴.
在和中,
,
∴≌(HL).
18.见解析
【解析】证明:
,
,
又,,
,
19.详见解析
【解析】
解:小军的作法有道理,理由如下:
过点B作BG∥AC交EF的延长线于点G,连接BE
∵
点E、F分别是AC、BC的中点
∴
AE=CE,
BF=CF
∵
BG∥AC
∴
∠ECF=∠GBF
,∠AEB=∠GBE
(两直线平行,内错角相等)
∵
∴
△ECF≌△GBF
(两角及其夹边对应相等的两个三角形全等)
∴
EF=GF
,CE=BG
(全等三角形的对应边相等)
∵
EF=GF
,EF+GF=EG
∴
EG=2EF
∵
CE=BG,
AE=CE
∴
AE=BG
∵
在△AEB和△GBE中,
∴
△AEB≌△GBE
(两边及其夹角对应相等的两个三角形全等)
∴
AB=GE
(全等三角形的对应边相等)
∵
GE=2EF,
AB=GE
∴
AB=2EF
故小军的做法是有道理的;
取直接能到达A,B两点的C点,延长BC,AC,使,,
连接DE,
在△ABC和△EDC中,
则,所以.
20.见解析
【解析】
等边中,∴,
∵线段绕点按顺时针方向旋转后得到,
∴,
∴,
即,
,
∴,
在与中,
∴(SAS)
∴,
∴
∴
21.详见解析
【解析】解:延长,交于点,
∵,,,
∴.
∵在和中,,
∴≌(ASA).∴.
∵在和中,,
∴≌(ASA).∴,即.
∴.
22.详见解析
【解析】在AC上截取AE=AB,连接PE,
∵AD平分,
∴.
在和中,
∴.
在中,,
∵,AE=AB,
∴.
23.(1)138°;(2)3.
【解析】(1)∵△ABE≌△ACD,
∴∠EBA=∠C=42°,
∴∠EBG=180°-42°=138°;
(2)∵△ABE≌△ACD,
∴AC=AB=9,AE=AD=6,
∴CE=AC-AE=9-6=3.
24.(1)详见解析;(2)详见解析.
【解析】解:(1)如图,延长至,使,
∵是中线,∴.
在和中,,
∴≌(SAS).∴,.
∵,∴.
∵,,∴.
∵,
∴.
在和中,,
∴≌(SAS).∴.
∵,∴.∴.
在中,,∴.
(2)如图,过点作交的延长线于,则,
∵,∴.
∵,∴.∴.
∵,,∴.
∵,
∴.
在和中,,
∴≌(AAS).∴.
∵,∴.
在和中,,
∴≌(AAS).∴.
答案第1页,总2页
答案第1页,总2页
12.2三角形全等的判定
时间:60分钟;
一、单选题
1.下列三角形中,能全等的是(
)
(1)一腰和顶角对应相等的两个等腰三角形;
(2)一腰和一个角分别相等的两个等腰三角形;
(3)有两边分别相等的两个直角三角形;
(4)两条直角边对应相等的两个直角三角形.
A.(1)(3)
B.(2)(4)
C.(1)(4)
D.(1)(3)(4)
2.用直尺和圆规作一个角等于已知角,如图,能得出的依据是(
)
A.
B.
C.
D.
3.如图,在△ABC中,AB=8,AC=6,AD是BC边上的中线,则AD长的取值范围是(
)
A.6
4.已知如图,AD∥BC,AB⊥BC,CD⊥DE,CD=ED,AD=2,BC=3,则△ADE的面积为( )
A.1
B.2
C.5
D.无法确定
5.如图,△ABC是一个什么三角形?(
)请说明理由.
A.等腰三角形;
B.等边三角形
C.直角三角形;
D.等腰直角三角形
6.如图,小强利用全等三角形的知识测量池塘两端M、N的距离,如果△PQO≌△NMO,则只需测出其长度的线段是(
)
A.PO
B.PQ
C.MO
D.MQ
7.如图所示,,,,结论:①;②;③;④,其中正确的是有(
)
A.1个
B.2个
C.3个
D.4个
8.如图,,,垂足分别为点,点,、相交于点O,,则图中全等三角形共有(
)
A.2对
B.3对
C.4对
D.5对
二、填空题
9.如图,已知△ABC的六个元素,其中a、b、c表示三角形三边的长,则下面甲、乙、丙三个三角形中和△ABC一定全等的图形是__.
10.如图,△ABC是不等边三角形,DE=BC,以D,E为两个顶点作位置不同的三角形,使所作的三角形与△ABC全等,这样的三角形最多可以画出______个.
11.如图所示,等腰直角三角形中,,,为的中点,.则四边形的面积为______.
12.如图,方格纸上有一个格点三角形和一条格点线段AB,在这个格点纸上找一点C,使得△ABC与这个格点三角形全等,这样的C点可以找到________个.
13.如图,在等边三角形ABC中,BD=CE,AD,BE交于点F,则_________;
14.在ABC中,AB=3,AC=4,则BC边上的中线AD的取值范围是_________
15.如图已知:AD平分∠BAC,AC=AB+BD,∠B=56°,求∠C=_____
16.如图,已知,,,则等于________.
三、解答题
17.如图,在中,是的中点,,,垂足分别是点、,.
(1)图中有几对全等的三角形?请一一列出;
(2)选择一对你认为全等的三角形进行证明.
18.如图,,,。求证:。
19.如图所示,要测量一个沼泽水潭的宽度.现由于不能直接测量,小军是这样操作的:他在平地上选取一点C,该点可以直接到达A与B点,接着他量出AC和BC的距离,并找出AC与BC的中点E、F,连接EF,测量EF的长,于是他便知道了水潭AB的长等于2EF,小军的做法有道理吗?说明理由.你还有比小军更简单的方法吗?
20.如图,在等边中,点是边上一点,连接,将线段绕点按顺时针方向旋转后得到,连接.求证:.
21.如图,在中,,,是上的一点,且的延长线交于,又平分,求证:.
22.如图所示,AD平分∠BAC,P是射线AD上一点,P与A不重合,.
求证:.
23.如图,CD⊥AB于点D,BE⊥AC于点E,△ABE≌△ACD,∠C=42°,AB=9,AD=6,G为AB延长线上一点.
(1)求∠EBG的度数.
(2)求CE的长.
24.已知,,,.直线过点,交、于点、.
(1)若是中线,求证:;
(2)若,求证:.
试卷第2页,总2页
参考答案
1.C
【解析】解:(1)两个等腰三角形的顶角相等,则两个底角也对应相等,所以一腰和顶角对应相等的两个等腰三角形全等,故符合题意;
(2)当一个三角形的底角和另一个三角形的顶角相等时,就不能推出两三角形全等,故本选项不符合题意;
(3)当一个三角形的斜边和另一个三角形的直角边相等,
如图,,但是两三角形不全等,
故本选项不符合题意;
(4)符合公理,能推出两直角三角形全等,故本选项符合题意;
故选:.
2.B
【解析】解:作图的步骤:
①以O为圆心,任意长为半径画弧,分别交OA、OB于点D、C;
②任意作一点O′,作射线O′B′,以O′为圆心,OC长为半径画弧,交O′B′于点C′;
③以C′为圆心,CD长为半径画弧,交前弧于点D′;
④过点D′作射线O′A′.
所以∠A′O′B′就是与∠AOB相等的角;
作图完毕.
在△OCD与△O′C′D′,
,
∴△OCD≌△O′C′D′(SSS),
∴∠A′O′B′=∠AOB,
显然运用的判定方法是SSS.
故选:B.
3.C
【解析】解:延长AD到E,使AD=DE,连接BE,如图所示:
∵AD=DE,∠ADC=∠BDE,BD=DC,
∴△ADC≌△EDB(SAS)
∴BE=AC=6,
在△AEB中,AB-BE<AE<AB+BE,
即8-6<2AD<8+6,
∴1<AD<7,
故选:C.
4.A
【解析】过D作BC的垂线交BC于G,过E作AD的垂线交AD的延长线于F,
∵∠EDF+∠FDC=90°,
∠GDC+∠FDC=90°,
∴∠EDF=∠GDC,
于是在Rt△EDF和Rt△CDG中,
,
∴△DEF≌△DCG,
∴EF=CG=BC﹣BG=BC﹣AD=3﹣2=1,
所以,S△ADE=(AD×EF)÷2=(2×1)÷2=1.
故选A.
5.D
【解析】如图,由题意知:AE=BD=2,CD=BE=1,∠AEB=∠BDC=90°,
在和中:
∴,
∴∠ABE=∠BCD,AB=BC,
又∵∠BCD+∠CBD=90°,
∴∠ABE+∠CBD=90°,
∴为等腰直角三角形,
故答案为:D.
6.B
【解析】解:要想利用△PQO≌△NMO求得MN的长,只需求得线段PQ的长,故选B.
7.C
【解析】解:∵,
∴△AEB≌△AFC;(AAS)
∴∠FAM=∠EAN,
∴∠EAN-∠MAN=∠FAM-∠MAN,即∠EAM=∠FAN;(故③正确)
又∵∠E=∠F=90°,AE=AF,
∴△EAM≌△FAN;(ASA)
∴EM=FN;(故①正确)
由△AEB≌△AFC知:∠B=∠C,AC=AB;
又∵∠CAB=∠BAC,
∴△ACN≌△ABM;(故④正确)
由于条件不足,无法证得②CD=DN;故正确的结论有:①③④;
故选:C.
8.C
【解析】解:∵CD⊥AB,BE⊥AC,
∴∠ADO=∠AEO=90°,
又∵∠1=∠2,AO=AO,
∴ADO≌AEO;(AAS)
∴OD=OE,AD=AE,
∵∠DOB=∠EOC,∠ODB=∠OEC=90°,OD=OE,
∴BOD≌COE;(ASA)
∴BD=CE,OB=OC,∠B=∠C,
∵AE=AD,∠DAC=∠CAB,∠ADC=∠AEB=90°
∴ADC≌AEB;(ASA)
∵AD=AE,BD=CE,
∴AB=AC,
∵OB=OC,AO=AO,
∴ABO≌ACO.(SSS)
所以共有四对全等三角形.
故选:C.
9.乙和丙
【解析】解:由SAS可知,图乙与△ABC全等,
由AAS可知,图丙与△ABC全等,
故答案为:乙和丙.
10.4
【解析】如图,能画4个,分别是:以D为圆心,AB为半径画圆;以C为圆心,CA为半径画圆.两圆相交于两点(DE上下各一个),分别于D、E连接后,可得到两个三角形;以D为圆心,AC为半径画圆;以E为圆心,AB为半径画圆.两圆相交于两点(DE上下各一个),分别于D、E连接后,可得到两个三角形.因此最多能画出4个
11.
【解析】(1)连接BO.
∵是等腰三角形,,,
∴,
又∵O是AC中点,
∴BO⊥AC,∠ABO=∠CBO=∠A=∠C=45°,BO=AO=CO=,
∵∠EOB+∠FOB=90°,∠FOB+∠COF=90°,
∴∠EOB=∠COF,
在△BEO和△CFO中,
,
∴,
∴.
12.4个
【解析】根据三边相等可得:有4个三角形可以和已知三角形全等.
13.60°
【解析】解:在等边△ABC中,AB=BC,∠ABC=∠C=60°,
在△ABD和△BCE中,
∵,
∴△ABD≌△BCE(SAS),
∴∠BAD=∠CBE,
在△ABF中,∠AFE=∠BAD+∠ABF=∠CBE+∠ABF=∠ABC=60°,
即∠AFE=60°.
故答案为:60°.
14.0.5<AD<3.5.
【解析】解:如图,延长AD到E,使DE=AD,
∵AD是BC边上的中线,
∴BD=CD,
在△ABD和△ECD中
,
∴△ABD≌△ECD(SAS),
∴CE=AB,
∵AB=3,AC=4,
∴4-3<AE<4+3,
即1<AE<7,
∴0.5<AD<3.5.
故答案为:0.5<AD<3.5.
15.31°.
【解析】如图,在AC上截取AE=AB,连接DE,
∵AD平分∠BAC,
∴∠BAD=∠EAD,
而AD是公共边,
∴△ABD≌△ADE,
∴∠B=∠AED=62°,DE=BD,
而AB+BD=AC=AE+CE,
∴DE=CE,
∴∠EDC=∠C,
而∠AED=∠C+∠EDC=62°,
∴∠C=31°.
16.
【解析】在和中,
∵,
,
,
,
故答案为40°.
17.(1)3对;分别是:≌.≌.≌;(2)见解析.
【解析】(1)解:3对.分别是:≌,≌,≌;
(2)以≌为例证明.
∵,,
∴.
又是的中点,
∴.
在和中,
,
∴≌(HL).
18.见解析
【解析】证明:
,
,
又,,
,
19.详见解析
【解析】
解:小军的作法有道理,理由如下:
过点B作BG∥AC交EF的延长线于点G,连接BE
∵
点E、F分别是AC、BC的中点
∴
AE=CE,
BF=CF
∵
BG∥AC
∴
∠ECF=∠GBF
,∠AEB=∠GBE
(两直线平行,内错角相等)
∵
∴
△ECF≌△GBF
(两角及其夹边对应相等的两个三角形全等)
∴
EF=GF
,CE=BG
(全等三角形的对应边相等)
∵
EF=GF
,EF+GF=EG
∴
EG=2EF
∵
CE=BG,
AE=CE
∴
AE=BG
∵
在△AEB和△GBE中,
∴
△AEB≌△GBE
(两边及其夹角对应相等的两个三角形全等)
∴
AB=GE
(全等三角形的对应边相等)
∵
GE=2EF,
AB=GE
∴
AB=2EF
故小军的做法是有道理的;
取直接能到达A,B两点的C点,延长BC,AC,使,,
连接DE,
在△ABC和△EDC中,
则,所以.
20.见解析
【解析】
等边中,∴,
∵线段绕点按顺时针方向旋转后得到,
∴,
∴,
即,
,
∴,
在与中,
∴(SAS)
∴,
∴
∴
21.详见解析
【解析】解:延长,交于点,
∵,,,
∴.
∵在和中,,
∴≌(ASA).∴.
∵在和中,,
∴≌(ASA).∴,即.
∴.
22.详见解析
【解析】在AC上截取AE=AB,连接PE,
∵AD平分,
∴.
在和中,
∴.
在中,,
∵,AE=AB,
∴.
23.(1)138°;(2)3.
【解析】(1)∵△ABE≌△ACD,
∴∠EBA=∠C=42°,
∴∠EBG=180°-42°=138°;
(2)∵△ABE≌△ACD,
∴AC=AB=9,AE=AD=6,
∴CE=AC-AE=9-6=3.
24.(1)详见解析;(2)详见解析.
【解析】解:(1)如图,延长至,使,
∵是中线,∴.
在和中,,
∴≌(SAS).∴,.
∵,∴.
∵,,∴.
∵,
∴.
在和中,,
∴≌(SAS).∴.
∵,∴.∴.
在中,,∴.
(2)如图,过点作交的延长线于,则,
∵,∴.
∵,∴.∴.
∵,,∴.
∵,
∴.
在和中,,
∴≌(AAS).∴.
∵,∴.
在和中,,
∴≌(AAS).∴.
答案第1页,总2页
答案第1页,总2页
