22.1 二次函数最值问题 强化练习卷 2021-2022学年年人教版数学九年级上册同步专题七(Word版 含答案)
文档属性
| 名称 | 22.1 二次函数最值问题 强化练习卷 2021-2022学年年人教版数学九年级上册同步专题七(Word版 含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 150.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-07 09:38:24 | ||
图片预览



文档简介
人教版数学九年级上册同步专题七
《二次函数最值问题》强化练习卷
一、选择题
1.若一次函数y=(a+1)x+a的图象过第一、三、四象限,则二次函数y=ax2-ax(
)
A.有最大值
B.有最大值-
C.有最小值
D.有最小值-
2.已知二次函数y=x2﹣4x+2,关于该函数在﹣1≤x≤3的取值范围内,下列说法正确的是( )
A.有最大值﹣1,有最小值﹣2
B.有最大值0,有最小值﹣1
C.有最大值7,有最小值﹣1
D.有最大值7,有最小值﹣2
3.已知抛物线y=0.25x2+1具有如下性质:该抛物线上任意一点到定点F(0,2)的距离与到x轴的距离始终相等,如图,点M的坐标为(,3),P是抛物线y=0.25x2+1上一个动点,
则△PMF周长的最小值是( )
A.3 B.4 C.5 D.6
4.已知二次函数y=ax2﹣bx+0.5b﹣a与x轴交于A、B两点,则线段AB的最小值为(
)
A.0.5
B.2
C.
D.无法确定
5.用min{a,b}表示a,b两数中的最小数,若函数,则y的图象为
6.如图,点A,B的坐标分别为(1,4)和(4,4),抛物线y=a(x-m)2+n的顶点在线段AB上运动,与x轴交于C,D两点(点C在点D的左侧).若点C的横坐标最小值为-3,则点D的横坐标最大值为(
)
A.-3
B.1
C.5
D.8
7.二次函数y=-(x-1)2+5,当m≤x≤n且mn<0时,y的最小值为2m,最大值为2n,则m+n的值为(
)
A.
B.2
C.
D.
8.如图,在△ABC中,∠C=90°,AB=10cm,BC=8cm,点P从点A沿AC向点C以1m/s的速度运动,同时点Q从点C沿CB向点B以2cm/s的速度运动(点Q运动到点B停止),在运动过程中,△PCQ面积的最大值为(
)
A.6
cm2
B.9
cm2
C.12
cm2
D.15
cm2
二、填空题
9.某农场拟建三间矩形种牛饲养室,饲养室的一面靠墙(墙长50m),中间用两道墙隔开(如图所示).已知计划中的建筑材料可建墙的总长度为48m,则这三间矩形种牛饲养室的总占地面积的最大值为
m2.
10.如图,在平面直角坐标系中,菱形OABC的顶点A在x轴正半轴上,顶点C的坐标为(4,3),D是抛物线y=-x2+6x上一点,且在x轴上方,则△BCD面积的最大值为
.
11.如图,二次函数y=-0.5x2-1.5x+2的图象与x轴交于A、B两点,与y轴交于C点,点D(m,n)是抛物线在第二象限的部分上的一动点,则四边形OCDA的面积的最大值是 .?
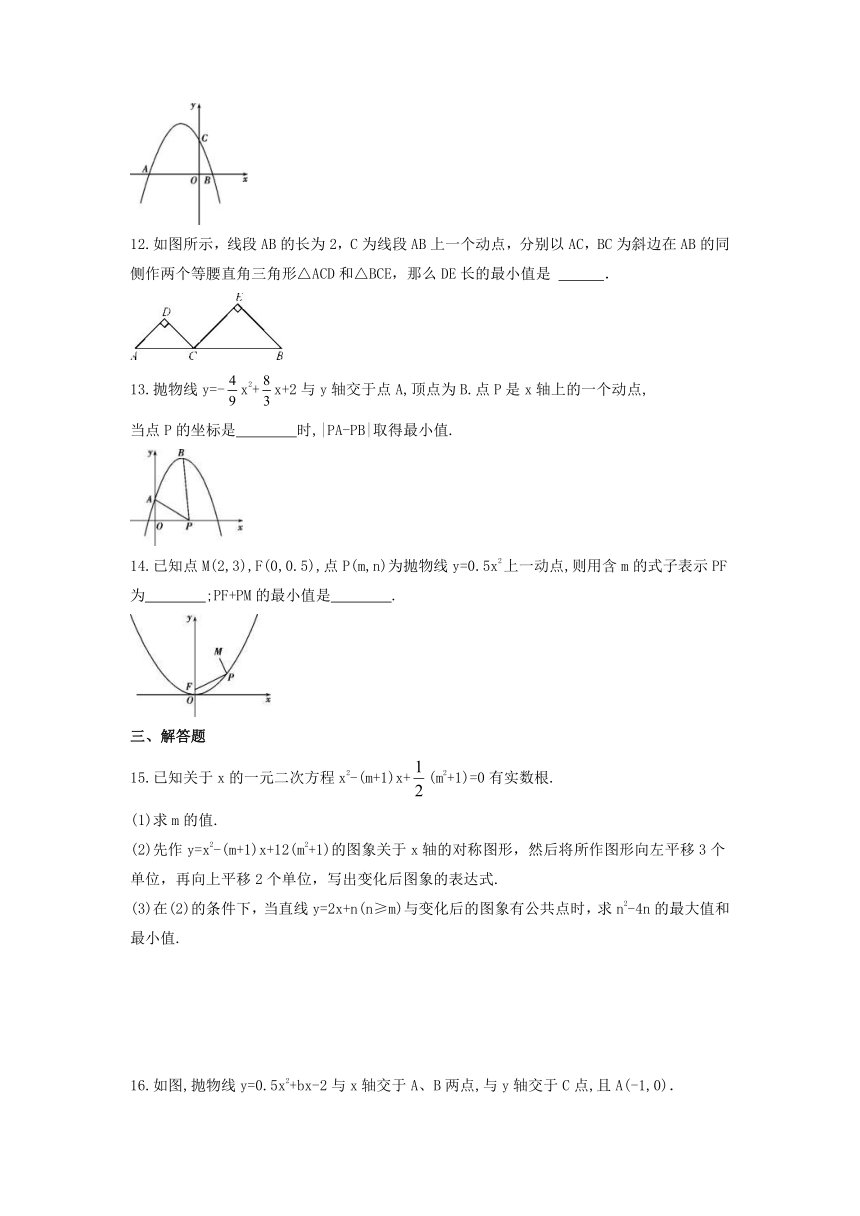
12.如图所示,线段AB的长为2,C为线段AB上一个动点,分别以AC,BC为斜边在AB的同侧作两个等腰直角三角形△ACD和△BCE,那么DE长的最小值是
.
13.抛物线y=-x2+x+2与y轴交于点A,顶点为B.点P是x轴上的一个动点,
当点P的坐标是 时,|PA-PB|取得最小值.?
14.已知点M(2,3),F(0,0.5),点P(m,n)为抛物线y=0.5x2上一动点,则用含m的式子表示PF为 ;PF+PM的最小值是 .?
三、解答题
15.已知关于x的一元二次方程x2-(m+1)x+(m2+1)=0有实数根.
(1)求m的值.
(2)先作y=x2-(m+1)x+12(m2+1)的图象关于x轴的对称图形,然后将所作图形向左平移3个单位,再向上平移2个单位,写出变化后图象的表达式.
(3)在(2)的条件下,当直线y=2x+n(n≥m)与变化后的图象有公共点时,求n2-4n的最大值和最小值.
16.如图,抛物线y=0.5x2+bx-2与x轴交于A、B两点,与y轴交于C点,且A(-1,0).
(1)求抛物线的解析式及顶点D的坐标;
(2)判断△ABC的形状,证明你的结论;
(3)点M是x轴上的一个动点,当△DCM的周长最小时,求点M的坐标.
17.某商店经销一种学生用双肩包,已知这种双肩包的成本价为每个30元.市场调查发现,这种双肩包每天的销售量y(个)与销售单价x(元)有如下关系:
y=﹣x+60(30≤x≤60).设这种双肩包每天的销售利润为w元.
(1)求w与x之间的函数关系式;
(2)这种双肩包销售单价定为多少元时,每天的销售利润最大?最大利润是多少元?
(3)如果物价部门规定这种双肩包的销售单价不高于42元,该商店销售这种双肩包每天要获得200元的销售利润,销售单价应定为多少元?
18.利民商店经销甲、乙两种商品.
现有如下信息:
请根据以上信息,解答下列问题:
(1)甲、乙两种商品的进货单价各多少元?
(2)该商店平均每天卖出甲商品500件和乙商品300件.经调查发现,甲、乙两种商品零售单价分别每降0.1元,这两种商品每天可各多销售100件.为了使每天获取更大的利润,商店决定把甲、乙两种商品的零售单价都下降m元.
在不考虑其他因素的条件下,当m定为多少时,才能使商店每天销售甲、乙两种商品获取的利润最大?每天的最大利润是多少?
参考答案
1.B.
2.D.
3.C.
4.C
5.A
6.D.
7.D.
8.B;
9.答案为:144.
10.答案为:15.
11.答案为:8.
12.答案为:1.
13.答案为:(,0)
14.答案为:0.5(m2+1);3.5.
15.解:(1)对于一元二次方程x2-(m+1)x+(m2+1)=0,
Δ=(m+1)2-4×(m2+1)=-m2+2m-1=-(m-1)2,
∵方程有实数根,
∴-(m-1)2≥0.
∴m=1.
(2)由(1)知y=x2-2x+1=(x-1)2,
它的图象关于x轴的对称图形的函数表达式为y=-(x-1)2,
∴平移后的表达式为y=-(x+2)2+2=-x2-4x-2.
(3)由,消去y得到x2+6x+n+2=0,
由题意知Δ≥0,
∴36-4(n+2)≥0.
∴n≤7.
∵n≥m,m=1,
∴1≤n≤7.
令y′=n2-4n=(n-2)2-4,
∴当n=2时,y′的值最小,最小值为-4,n=7时,y′的值最大,最大值为21.
∴n2-4n的最大值为21,最小值为-4.
16.解:(1)∵点在抛物线上,
∴,∴,∴抛物线的解析式为.
∵,
∴顶点D的坐标为.?
(2)△ABC是直角三角形.当时,,∴,则.
当时,,∴,则.
?∴,,?
∴.
∵,,,
∴,
∴△ABC是直角三角形.?
(3)作出点C关于轴的对称点C′,则.连接C′D交轴于点M,根据轴对称性及两点之间线段最短可知,CD一定,当MC+MD的值最小时,△CDM的周长最小.??
设直线C′D的解析式为,则:则,解得,
∴?当时,,则,∴.?
17.解:
18.解:(1)设甲商品的进货单价是x元,乙商品的进货单价是y元.据题意,得解得
答:甲商品的进货单价是2元,乙商品的进货单价是3元.
(2)设商店每天销售甲、乙两种商品获取的利润为s元,则
s=(1-m)(500+100×)+(5-3-m)(300+100×)
即s=-2000m2+2200m+1100=-2000(m-0.55)2+1705.
∴当m=0.55时,s有最大值,最大值为1705.
答:当m定为0.55时,才能使商店每天销售甲、乙两种商品获取的利润最大,每天的最大利润是1705元.
《二次函数最值问题》强化练习卷
一、选择题
1.若一次函数y=(a+1)x+a的图象过第一、三、四象限,则二次函数y=ax2-ax(
)
A.有最大值
B.有最大值-
C.有最小值
D.有最小值-
2.已知二次函数y=x2﹣4x+2,关于该函数在﹣1≤x≤3的取值范围内,下列说法正确的是( )
A.有最大值﹣1,有最小值﹣2
B.有最大值0,有最小值﹣1
C.有最大值7,有最小值﹣1
D.有最大值7,有最小值﹣2
3.已知抛物线y=0.25x2+1具有如下性质:该抛物线上任意一点到定点F(0,2)的距离与到x轴的距离始终相等,如图,点M的坐标为(,3),P是抛物线y=0.25x2+1上一个动点,
则△PMF周长的最小值是( )
A.3 B.4 C.5 D.6
4.已知二次函数y=ax2﹣bx+0.5b﹣a与x轴交于A、B两点,则线段AB的最小值为(
)
A.0.5
B.2
C.
D.无法确定
5.用min{a,b}表示a,b两数中的最小数,若函数,则y的图象为
6.如图,点A,B的坐标分别为(1,4)和(4,4),抛物线y=a(x-m)2+n的顶点在线段AB上运动,与x轴交于C,D两点(点C在点D的左侧).若点C的横坐标最小值为-3,则点D的横坐标最大值为(
)
A.-3
B.1
C.5
D.8
7.二次函数y=-(x-1)2+5,当m≤x≤n且mn<0时,y的最小值为2m,最大值为2n,则m+n的值为(
)
A.
B.2
C.
D.
8.如图,在△ABC中,∠C=90°,AB=10cm,BC=8cm,点P从点A沿AC向点C以1m/s的速度运动,同时点Q从点C沿CB向点B以2cm/s的速度运动(点Q运动到点B停止),在运动过程中,△PCQ面积的最大值为(
)
A.6
cm2
B.9
cm2
C.12
cm2
D.15
cm2
二、填空题
9.某农场拟建三间矩形种牛饲养室,饲养室的一面靠墙(墙长50m),中间用两道墙隔开(如图所示).已知计划中的建筑材料可建墙的总长度为48m,则这三间矩形种牛饲养室的总占地面积的最大值为
m2.
10.如图,在平面直角坐标系中,菱形OABC的顶点A在x轴正半轴上,顶点C的坐标为(4,3),D是抛物线y=-x2+6x上一点,且在x轴上方,则△BCD面积的最大值为
.
11.如图,二次函数y=-0.5x2-1.5x+2的图象与x轴交于A、B两点,与y轴交于C点,点D(m,n)是抛物线在第二象限的部分上的一动点,则四边形OCDA的面积的最大值是 .?
12.如图所示,线段AB的长为2,C为线段AB上一个动点,分别以AC,BC为斜边在AB的同侧作两个等腰直角三角形△ACD和△BCE,那么DE长的最小值是
.
13.抛物线y=-x2+x+2与y轴交于点A,顶点为B.点P是x轴上的一个动点,
当点P的坐标是 时,|PA-PB|取得最小值.?
14.已知点M(2,3),F(0,0.5),点P(m,n)为抛物线y=0.5x2上一动点,则用含m的式子表示PF为 ;PF+PM的最小值是 .?
三、解答题
15.已知关于x的一元二次方程x2-(m+1)x+(m2+1)=0有实数根.
(1)求m的值.
(2)先作y=x2-(m+1)x+12(m2+1)的图象关于x轴的对称图形,然后将所作图形向左平移3个单位,再向上平移2个单位,写出变化后图象的表达式.
(3)在(2)的条件下,当直线y=2x+n(n≥m)与变化后的图象有公共点时,求n2-4n的最大值和最小值.
16.如图,抛物线y=0.5x2+bx-2与x轴交于A、B两点,与y轴交于C点,且A(-1,0).
(1)求抛物线的解析式及顶点D的坐标;
(2)判断△ABC的形状,证明你的结论;
(3)点M是x轴上的一个动点,当△DCM的周长最小时,求点M的坐标.
17.某商店经销一种学生用双肩包,已知这种双肩包的成本价为每个30元.市场调查发现,这种双肩包每天的销售量y(个)与销售单价x(元)有如下关系:
y=﹣x+60(30≤x≤60).设这种双肩包每天的销售利润为w元.
(1)求w与x之间的函数关系式;
(2)这种双肩包销售单价定为多少元时,每天的销售利润最大?最大利润是多少元?
(3)如果物价部门规定这种双肩包的销售单价不高于42元,该商店销售这种双肩包每天要获得200元的销售利润,销售单价应定为多少元?
18.利民商店经销甲、乙两种商品.
现有如下信息:
请根据以上信息,解答下列问题:
(1)甲、乙两种商品的进货单价各多少元?
(2)该商店平均每天卖出甲商品500件和乙商品300件.经调查发现,甲、乙两种商品零售单价分别每降0.1元,这两种商品每天可各多销售100件.为了使每天获取更大的利润,商店决定把甲、乙两种商品的零售单价都下降m元.
在不考虑其他因素的条件下,当m定为多少时,才能使商店每天销售甲、乙两种商品获取的利润最大?每天的最大利润是多少?
参考答案
1.B.
2.D.
3.C.
4.C
5.A
6.D.
7.D.
8.B;
9.答案为:144.
10.答案为:15.
11.答案为:8.
12.答案为:1.
13.答案为:(,0)
14.答案为:0.5(m2+1);3.5.
15.解:(1)对于一元二次方程x2-(m+1)x+(m2+1)=0,
Δ=(m+1)2-4×(m2+1)=-m2+2m-1=-(m-1)2,
∵方程有实数根,
∴-(m-1)2≥0.
∴m=1.
(2)由(1)知y=x2-2x+1=(x-1)2,
它的图象关于x轴的对称图形的函数表达式为y=-(x-1)2,
∴平移后的表达式为y=-(x+2)2+2=-x2-4x-2.
(3)由,消去y得到x2+6x+n+2=0,
由题意知Δ≥0,
∴36-4(n+2)≥0.
∴n≤7.
∵n≥m,m=1,
∴1≤n≤7.
令y′=n2-4n=(n-2)2-4,
∴当n=2时,y′的值最小,最小值为-4,n=7时,y′的值最大,最大值为21.
∴n2-4n的最大值为21,最小值为-4.
16.解:(1)∵点在抛物线上,
∴,∴,∴抛物线的解析式为.
∵,
∴顶点D的坐标为.?
(2)△ABC是直角三角形.当时,,∴,则.
当时,,∴,则.
?∴,,?
∴.
∵,,,
∴,
∴△ABC是直角三角形.?
(3)作出点C关于轴的对称点C′,则.连接C′D交轴于点M,根据轴对称性及两点之间线段最短可知,CD一定,当MC+MD的值最小时,△CDM的周长最小.??
设直线C′D的解析式为,则:则,解得,
∴?当时,,则,∴.?
17.解:
18.解:(1)设甲商品的进货单价是x元,乙商品的进货单价是y元.据题意,得解得
答:甲商品的进货单价是2元,乙商品的进货单价是3元.
(2)设商店每天销售甲、乙两种商品获取的利润为s元,则
s=(1-m)(500+100×)+(5-3-m)(300+100×)
即s=-2000m2+2200m+1100=-2000(m-0.55)2+1705.
∴当m=0.55时,s有最大值,最大值为1705.
答:当m定为0.55时,才能使商店每天销售甲、乙两种商品获取的利润最大,每天的最大利润是1705元.
同课章节目录
