京改版七年级上册数学 1.3相反数与绝对值3教案
文档属性
| 名称 | 京改版七年级上册数学 1.3相反数与绝对值3教案 |

|
|
| 格式 | docx | ||
| 文件大小 | 85.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-06 00:00:00 | ||
图片预览


文档简介
教
案
教学基本信息
课题
相反数与绝对值(3)
学科
数学
学段:
义务教育
年级
七年级
教材
书名:
义务教育教科书
出版社:
北京出版社
出版日期:2013
年12
月
教学目标及教学重点、难点
教学目标:
1.理解的含义,借助数轴理解绝对值的意义;并能熟练地求一个有理数的绝对值.
2.会利用绝对值比较两个负数的大小,将负数的大小比较转化为正数的大小比较,体会转化的数学思想.
3.理解相反数与绝对值之间的关系,能利用数轴解决相关的问题,体会数形结合的思想。
教学重点:利用数轴解决相关的相反数与绝对值的问题.
教学难点:利用数轴解决相关的相反数与绝对值的问题.
教学过程(表格描述)
教学环节
主要教学活动
设置意图
知识回顾
思考:数轴上点A与点A表示的数a之间的关系:
点A在原点的左侧或右侧
数a的正负性
点A到原点的距离
数a的绝对值:
引例 在数轴上把表示3和-3、-3.5的点表示出来,并回答以下问题:
(1)指出表示3和-3这两个点到原点的距离,这两个距离有什么关系?
(2)在数轴上距离原点3.5个单位长度的点有几个,在数轴上表示出来?
(3)-3和-3.5两个点中哪一个在右边,哪一个离原点较远?
解:(1)表示3与-3的两个点到原点的距离是3,距离相等
(2)在数轴上距离原点个单位长度的点有2个
(3)表示-3的点在表示的点的右边,表示的点离原点较远
思考:
1、-3的相反数是多少?
2、3与-3的绝对值分别是多少?有什么关系?
3、若,求a;若,求a;若,则a的值是多少?
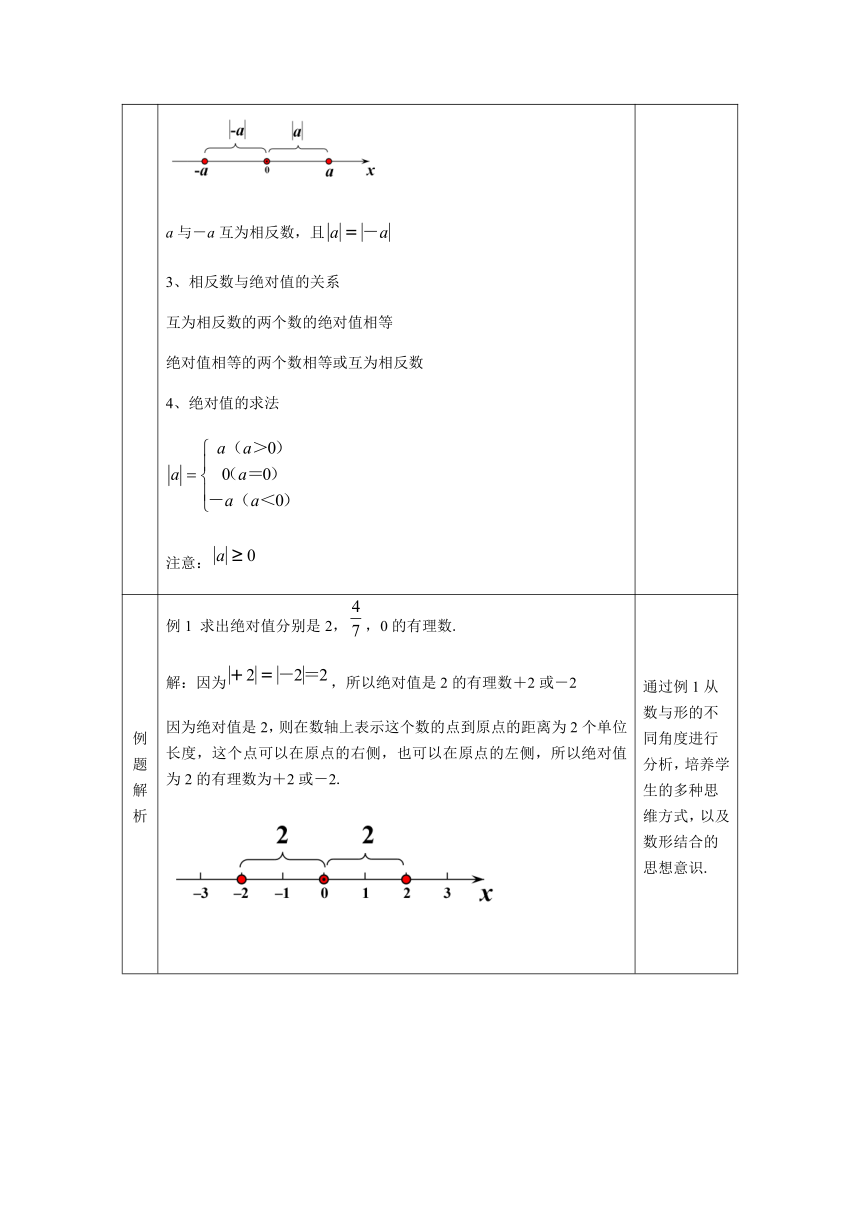
2、相反数:
(形)位于原的的两侧,到原点的距离相等的两个点表示的两个数
(数)符号相反,绝对值相等的两个数
a与-a互为相反数,且
3、相反数与绝对值的关系
互为相反数的两个数的绝对值相等
绝对值相等的两个数相等或互为相反数
4、绝对值的求法
注意:
回顾上节课所学知识和方法,为本节课做铺垫.
通过引例,以题带点复习上节课的知识
例题解析
例1
求出绝对值分别是2,,0的有理数.
解:因为,所以绝对值是2的有理数+2或-2
因为绝对值是2,则在数轴上表示这个数的点到原点的距离为2个单位长度,这个点可以在原点的右侧,也可以在原点的左侧,所以绝对值为2的有理数为+2或-2.
通过例1从数与形的不同角度进行分析,培养学生的多种思维方式,以及数形结合的思想意识.
例题解析
例2 比较的大小。
分析:由于在数轴上右边的点所表示的数大于左边的点表示的数,两个负数越是右边的点表示的负数离原点越近,即绝对值越小,故两个负数中,绝对值越小的数反而大。
解:因为
又因为
所以
两个负数的比较转化为两个负数的绝对值的比较,体会转化的数学思想.
拓展提高
例3 有理数a、b、c、d在数轴上对应点的位置如图所示,若有理数b、d互为相反数,则这四个有理数中,绝对值最小的是( )
A a
B
b
C
c
D
d
例4 有理数a、b在数轴上所对应的点如图所示,用“>”、“=”、“<”填空:
(1)a b
(2)
(3)
(4)
(5)
-a -b
例5
已知,求x,y的值。
解:因为,所以,
又因为,所以,
所以x=2,y=3.
深化理解相反数、绝对值的几何意义。
利用数轴理解相反数、绝对值的意义,培养数形结合的意识。
绝对值的非负性的应用。
课堂小结
1、绝对值的意义
2、任何一个有理数包含几个部分?
3、两个数的绝对值的相等,则这两个数的有什么数量关系?
培养学生归纳总结能力及语言表达能力
布置作业
1.回答下列问题,并说明理由:
(1)绝对值是的数有几个?是什么?
(2)绝对值是0的数有几个?是什么?
(3)有没有绝对值是-3.5的数?
2.比较下列各对数的大小
(1)-1.8和-2.01
(2)
和
;
(3)
和
;
(4)和。
3.如图,数轴上的A点所表示的是有理数a,则点A到原点的距离是(
)
A.
a
B.
–a
C.
±a
D.
4.填空:
(1)
的相反数是 ;
(2)-3.5的绝对值的相反数是 ;
(3)-0.5的相反数的绝对值是 ;
(4)若
,则x= ;
(5)绝对值小于3的整数有 个,最小的整数是 .
巩固所学知识
案
教学基本信息
课题
相反数与绝对值(3)
学科
数学
学段:
义务教育
年级
七年级
教材
书名:
义务教育教科书
出版社:
北京出版社
出版日期:2013
年12
月
教学目标及教学重点、难点
教学目标:
1.理解的含义,借助数轴理解绝对值的意义;并能熟练地求一个有理数的绝对值.
2.会利用绝对值比较两个负数的大小,将负数的大小比较转化为正数的大小比较,体会转化的数学思想.
3.理解相反数与绝对值之间的关系,能利用数轴解决相关的问题,体会数形结合的思想。
教学重点:利用数轴解决相关的相反数与绝对值的问题.
教学难点:利用数轴解决相关的相反数与绝对值的问题.
教学过程(表格描述)
教学环节
主要教学活动
设置意图
知识回顾
思考:数轴上点A与点A表示的数a之间的关系:
点A在原点的左侧或右侧
数a的正负性
点A到原点的距离
数a的绝对值:
引例 在数轴上把表示3和-3、-3.5的点表示出来,并回答以下问题:
(1)指出表示3和-3这两个点到原点的距离,这两个距离有什么关系?
(2)在数轴上距离原点3.5个单位长度的点有几个,在数轴上表示出来?
(3)-3和-3.5两个点中哪一个在右边,哪一个离原点较远?
解:(1)表示3与-3的两个点到原点的距离是3,距离相等
(2)在数轴上距离原点个单位长度的点有2个
(3)表示-3的点在表示的点的右边,表示的点离原点较远
思考:
1、-3的相反数是多少?
2、3与-3的绝对值分别是多少?有什么关系?
3、若,求a;若,求a;若,则a的值是多少?
2、相反数:
(形)位于原的的两侧,到原点的距离相等的两个点表示的两个数
(数)符号相反,绝对值相等的两个数
a与-a互为相反数,且
3、相反数与绝对值的关系
互为相反数的两个数的绝对值相等
绝对值相等的两个数相等或互为相反数
4、绝对值的求法
注意:
回顾上节课所学知识和方法,为本节课做铺垫.
通过引例,以题带点复习上节课的知识
例题解析
例1
求出绝对值分别是2,,0的有理数.
解:因为,所以绝对值是2的有理数+2或-2
因为绝对值是2,则在数轴上表示这个数的点到原点的距离为2个单位长度,这个点可以在原点的右侧,也可以在原点的左侧,所以绝对值为2的有理数为+2或-2.
通过例1从数与形的不同角度进行分析,培养学生的多种思维方式,以及数形结合的思想意识.
例题解析
例2 比较的大小。
分析:由于在数轴上右边的点所表示的数大于左边的点表示的数,两个负数越是右边的点表示的负数离原点越近,即绝对值越小,故两个负数中,绝对值越小的数反而大。
解:因为
又因为
所以
两个负数的比较转化为两个负数的绝对值的比较,体会转化的数学思想.
拓展提高
例3 有理数a、b、c、d在数轴上对应点的位置如图所示,若有理数b、d互为相反数,则这四个有理数中,绝对值最小的是( )
A a
B
b
C
c
D
d
例4 有理数a、b在数轴上所对应的点如图所示,用“>”、“=”、“<”填空:
(1)a b
(2)
(3)
(4)
(5)
-a -b
例5
已知,求x,y的值。
解:因为,所以,
又因为,所以,
所以x=2,y=3.
深化理解相反数、绝对值的几何意义。
利用数轴理解相反数、绝对值的意义,培养数形结合的意识。
绝对值的非负性的应用。
课堂小结
1、绝对值的意义
2、任何一个有理数包含几个部分?
3、两个数的绝对值的相等,则这两个数的有什么数量关系?
培养学生归纳总结能力及语言表达能力
布置作业
1.回答下列问题,并说明理由:
(1)绝对值是的数有几个?是什么?
(2)绝对值是0的数有几个?是什么?
(3)有没有绝对值是-3.5的数?
2.比较下列各对数的大小
(1)-1.8和-2.01
(2)
和
;
(3)
和
;
(4)和。
3.如图,数轴上的A点所表示的是有理数a,则点A到原点的距离是(
)
A.
a
B.
–a
C.
±a
D.
4.填空:
(1)
的相反数是 ;
(2)-3.5的绝对值的相反数是 ;
(3)-0.5的相反数的绝对值是 ;
(4)若
,则x= ;
(5)绝对值小于3的整数有 个,最小的整数是 .
巩固所学知识
同课章节目录
- 第一章 有理数
- 1.1 负数的引入
- 1.2 用数轴上的点表示有理数
- 1.3 相反数和绝对值
- 1.4 有理数的加法
- 1.5 有理数的减法
- 1.6 有理数加减法的混合运算
- 1.7 有理数的乘法
- 1.8 有理数的除法
- 1.9 有理数的乘方
- 1.10 有理数的混合运算
- 1.11 数的近似和科学记数法
- 1.12 用计算器做有理数的混合运算
- 第二章 一元一次方程
- 2.1 字母表示数
- 2.2 同类项与合并同类项
- 2.3 等式与方程
- 2.4 等式的基本性质
- 2.5 一元一次方程
- 2.6 列方程解应用问题
- 第三章 简单的几何图形
- 3.1 平面图形与立体图形
- 3.2 某些立体图形的展开图
- 3.3 从不同方向观察立体图形
- 3.4 点、线、面、体
- 3.5 直线、射线、线段
- 3.6 角及其分类
- 3.7 角的度量与角的换算
- 3.8 角平分线
- 3.9 两条直线的位置关系
- 3.10 相交线与平行线
- 3.11 用计算机绘图
