京改版七年级上册数学 3.10相交线与平行线(2)-1教案
文档属性
| 名称 | 京改版七年级上册数学 3.10相交线与平行线(2)-1教案 |
|
|
| 格式 | docx | ||
| 文件大小 | 171.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-06 00:00:00 | ||
图片预览


文档简介
教
案
教学基本信息
课题
相交线与平行线(2)
学科
数学
学段:
初中
年级
初一年级
教材
书名:《数学》七年级上册
出版社:北京出版社
出版日期:2016
年
4
月
教学目标及教学重点、难点
教学目标:
1.理解点到直线的距离、垂线段、平行线的概念;能度量点到直线的距离;
掌握结论:线外一点与直线上各点连接的所有线段中,垂线段最短.
2.经历探索概念、结论、画图和度量的过程,提升观察发现、归纳问题的能力.
3.在学习和探索的过程中,增强学习兴趣.
教学重点:垂线段的概念;平行线的概念;度量点到直线的距离.
教学难点:结论的应用.
教学过程(表格描述)
教学环节
主要教学活动
设置意图
引入
一、点到直线的距离
通过上节课的学习,我们已经知道如何过一点画已知直线的垂线,大家看这道题,按要求画一画、测一测:
【实践一】
如图,P是直线
l
外一点,过点P作直线
l
的垂线,垂足为点A.
垂线是一条直线,这节课我们进一步研究垂线上的点P到垂足间的这条线段.
回顾旧知,引入新课.
新课
一、点到直线的距离
1.定义:从直线外一点向这条直线引垂线,该点到垂足之间的线段叫做垂线段.
如图,线段PA就是点P到直线l的垂线段;
垂线段PA的长度,叫做点P到直线l的距离.
2.定义:从直线外一点到这条直线的垂线段的长度,叫做点到直线的距离.
图中,测量得到垂线段PA=3.6cm,那么点P到直线l的距离就等于3.6cm.
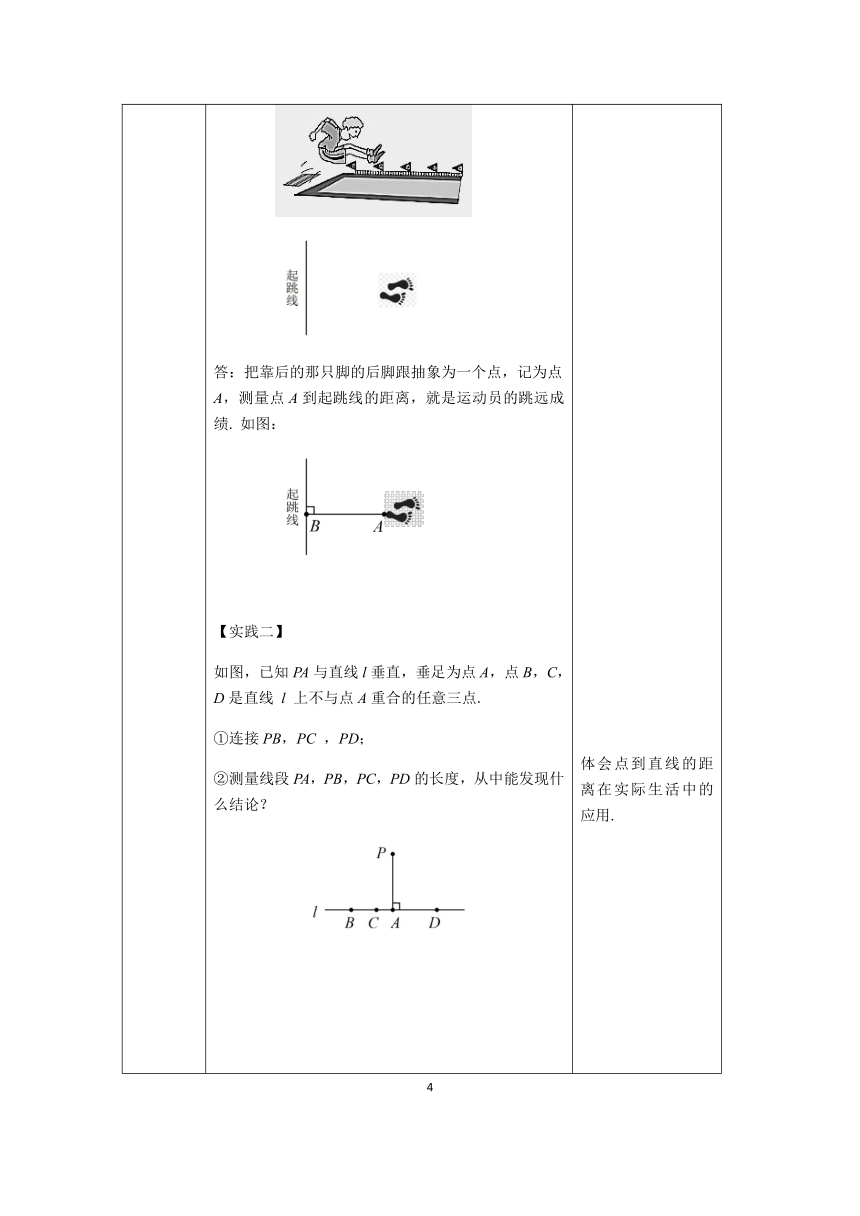
例1.如图,∠ACB=90°,CD⊥AB于点D,则点C到AB所在直线的距离是线段
的长度,线段AC的长度是点A到
所在直线的距离,点B到线段AC所在直线的距离是线段
的长度.
答案:CD,BC,BC.
练习1.
如图,点A在直线a上,点B在直线b上.
(
(1)怎样量出A,B两点间的距离?
(
(2)怎样量出点A到直线b的距离?
怎样量出点B到直线a的距离?
练习2.
如图,作出点A到线段BC所在直线的垂线段,垂足为点D,并测量点A到线段BC所在直线的距离.
(1)
(2)
【思考】
((u))
如图,如何测量运动员的跳远成绩?
答:把靠后的那只脚的后脚跟抽象为一个点,记为点A,测量点A到起跳线的距离,就是运动员的跳远成绩.
如图:
【实践二】
如图,已知PA与直线l垂直,垂足为点A,点B,C,D是直线
l
上不与点A重合的任意三点.
①连接PB,PC
,PD;
②测量线段PA,PB,PC,PD的长度,从中能发现什么结论?
通过测量,得到PA=4.5cm,PB=6.4cm,PC=5cm,PD=5.7cm.
3.结论:直线外一点与直线上各点连接的所有线段中,垂线段最短.
简称,垂线段最短.
例2.计划把河中的水引到水池C中(如图所示),可以先作CD⊥AB,垂足为D,然后沿CD开渠,则能使水渠最短,这种设计方案的根据是___________.
答案:垂线段最短.
例3.直线l外一点P到直线l上一点Q的距离是2cm,则点P到直线l的距离(
)
A.等于2cm
B.小于2cm
C.小于或等于2cm
D.大于2cm
答案:C.
分析:点P到直线l的距离是点P到直线l的垂线段的长度,如图:
①当PQ⊥l时,距离是2cm;
②当PQ与l不垂直时,根据“垂线段最短”,得到距离小于2cm.
平行线
如图,让直线PA绕点P旋转起来,使之与直线l没有交点,此时直线PA
与直线l是什么位置关系呢?
答:互相平行.
日常生活中我们见到笔直的列车轨道和斑马线,都给我们平行的印象:
1.定义:在同一平面内,不相交的两条直线叫做平行线.也说这两条直线互相平行.
图中,直线a与b就是两条平行线.
2.表示方法:平行用符号“∥”表示,读作“平行于”.直线a与b互相平行,记作a∥b或b∥a.
注意:定义中,不能直接说“不相交的两条直线叫做平行线”,必须加上“在同一平面内”.
如图,在长方体中,直线GF和直线AB没有公共点、不相交,但却不是平行线,因为它们不在同一平面内.
练习:观察图中所示的长方体,完成填空:
(1)用符号表示下列两棱所在直线的位置关系:
AB
DC,AD
AB,DH
HG,AE
BF;
(2)DC和BF所在直线是两条不相交的直线,它们
(填“是”或“不是”)平行线,因为只有
内,两条不相交的直线才能叫做平行线.
答案:(1)∥,⊥,⊥,∥;
(2)不是,在同一平面.
分析:
平行线的特点有两点:①在同一平面内
②不相交
加深对点到直线的距离的理解.
会测量点到直线的距离.
体会点到直线的距离在实际生活中的应用.
通过动手实践,提高探究和归纳能力.
应用“直线外一点与直线上各点连接的所有线段中,垂线段最短”解决问题.
联系生活实际,加深对平行线的印象.
加深对平行线概念的理解.
会判断两条直线的位置关系.
总结
两条直线的
位置关系
下面我们对这部分知识进行总结.
我们学习了两条直线的位置关系,包括:相交和不相交.
当两条直线只有一个公共点时,称它们为相交直线.
相交所成的四个角中,当其中一个角等于90°时,称它们互相垂直,是相交时的一种特殊情况.
希望大家掌握垂直的概念和符号表示,会过一点画已知直线的垂线,并能理解,这个点到垂足之间的线段叫做垂线段,这条垂线段的长度叫做这个点到直线的距离.
两条直线不相交,且在同一平面内,称它们为平行线;
两条直线不相交,不在同一平面内,这种位置关系大家高中会进一步学习.
帮助学生明确学习重点,将新知识纳入到已有知识系统中.
作业
1.作出点B到线段AC所在直线的垂线段,垂足为点D;并测量点B到线段AC所在直线的距离.
(1)
(2)
2.观察图中所示的长方体,完成填空:
(1)用符号表示下列两棱所在直线的位置关系:
HD
GC,FB
AB;
(2)AD和GC所在直线
(填“是”或“不是”)平行线,理由是
.
巩固所学新知.
11
案
教学基本信息
课题
相交线与平行线(2)
学科
数学
学段:
初中
年级
初一年级
教材
书名:《数学》七年级上册
出版社:北京出版社
出版日期:2016
年
4
月
教学目标及教学重点、难点
教学目标:
1.理解点到直线的距离、垂线段、平行线的概念;能度量点到直线的距离;
掌握结论:线外一点与直线上各点连接的所有线段中,垂线段最短.
2.经历探索概念、结论、画图和度量的过程,提升观察发现、归纳问题的能力.
3.在学习和探索的过程中,增强学习兴趣.
教学重点:垂线段的概念;平行线的概念;度量点到直线的距离.
教学难点:结论的应用.
教学过程(表格描述)
教学环节
主要教学活动
设置意图
引入
一、点到直线的距离
通过上节课的学习,我们已经知道如何过一点画已知直线的垂线,大家看这道题,按要求画一画、测一测:
【实践一】
如图,P是直线
l
外一点,过点P作直线
l
的垂线,垂足为点A.
垂线是一条直线,这节课我们进一步研究垂线上的点P到垂足间的这条线段.
回顾旧知,引入新课.
新课
一、点到直线的距离
1.定义:从直线外一点向这条直线引垂线,该点到垂足之间的线段叫做垂线段.
如图,线段PA就是点P到直线l的垂线段;
垂线段PA的长度,叫做点P到直线l的距离.
2.定义:从直线外一点到这条直线的垂线段的长度,叫做点到直线的距离.
图中,测量得到垂线段PA=3.6cm,那么点P到直线l的距离就等于3.6cm.
例1.如图,∠ACB=90°,CD⊥AB于点D,则点C到AB所在直线的距离是线段
的长度,线段AC的长度是点A到
所在直线的距离,点B到线段AC所在直线的距离是线段
的长度.
答案:CD,BC,BC.
练习1.
如图,点A在直线a上,点B在直线b上.
(
(1)怎样量出A,B两点间的距离?
(
(2)怎样量出点A到直线b的距离?
怎样量出点B到直线a的距离?
练习2.
如图,作出点A到线段BC所在直线的垂线段,垂足为点D,并测量点A到线段BC所在直线的距离.
(1)
(2)
【思考】
((u))
如图,如何测量运动员的跳远成绩?
答:把靠后的那只脚的后脚跟抽象为一个点,记为点A,测量点A到起跳线的距离,就是运动员的跳远成绩.
如图:
【实践二】
如图,已知PA与直线l垂直,垂足为点A,点B,C,D是直线
l
上不与点A重合的任意三点.
①连接PB,PC
,PD;
②测量线段PA,PB,PC,PD的长度,从中能发现什么结论?
通过测量,得到PA=4.5cm,PB=6.4cm,PC=5cm,PD=5.7cm.
3.结论:直线外一点与直线上各点连接的所有线段中,垂线段最短.
简称,垂线段最短.
例2.计划把河中的水引到水池C中(如图所示),可以先作CD⊥AB,垂足为D,然后沿CD开渠,则能使水渠最短,这种设计方案的根据是___________.
答案:垂线段最短.
例3.直线l外一点P到直线l上一点Q的距离是2cm,则点P到直线l的距离(
)
A.等于2cm
B.小于2cm
C.小于或等于2cm
D.大于2cm
答案:C.
分析:点P到直线l的距离是点P到直线l的垂线段的长度,如图:
①当PQ⊥l时,距离是2cm;
②当PQ与l不垂直时,根据“垂线段最短”,得到距离小于2cm.
平行线
如图,让直线PA绕点P旋转起来,使之与直线l没有交点,此时直线PA
与直线l是什么位置关系呢?
答:互相平行.
日常生活中我们见到笔直的列车轨道和斑马线,都给我们平行的印象:
1.定义:在同一平面内,不相交的两条直线叫做平行线.也说这两条直线互相平行.
图中,直线a与b就是两条平行线.
2.表示方法:平行用符号“∥”表示,读作“平行于”.直线a与b互相平行,记作a∥b或b∥a.
注意:定义中,不能直接说“不相交的两条直线叫做平行线”,必须加上“在同一平面内”.
如图,在长方体中,直线GF和直线AB没有公共点、不相交,但却不是平行线,因为它们不在同一平面内.
练习:观察图中所示的长方体,完成填空:
(1)用符号表示下列两棱所在直线的位置关系:
AB
DC,AD
AB,DH
HG,AE
BF;
(2)DC和BF所在直线是两条不相交的直线,它们
(填“是”或“不是”)平行线,因为只有
内,两条不相交的直线才能叫做平行线.
答案:(1)∥,⊥,⊥,∥;
(2)不是,在同一平面.
分析:
平行线的特点有两点:①在同一平面内
②不相交
加深对点到直线的距离的理解.
会测量点到直线的距离.
体会点到直线的距离在实际生活中的应用.
通过动手实践,提高探究和归纳能力.
应用“直线外一点与直线上各点连接的所有线段中,垂线段最短”解决问题.
联系生活实际,加深对平行线的印象.
加深对平行线概念的理解.
会判断两条直线的位置关系.
总结
两条直线的
位置关系
下面我们对这部分知识进行总结.
我们学习了两条直线的位置关系,包括:相交和不相交.
当两条直线只有一个公共点时,称它们为相交直线.
相交所成的四个角中,当其中一个角等于90°时,称它们互相垂直,是相交时的一种特殊情况.
希望大家掌握垂直的概念和符号表示,会过一点画已知直线的垂线,并能理解,这个点到垂足之间的线段叫做垂线段,这条垂线段的长度叫做这个点到直线的距离.
两条直线不相交,且在同一平面内,称它们为平行线;
两条直线不相交,不在同一平面内,这种位置关系大家高中会进一步学习.
帮助学生明确学习重点,将新知识纳入到已有知识系统中.
作业
1.作出点B到线段AC所在直线的垂线段,垂足为点D;并测量点B到线段AC所在直线的距离.
(1)
(2)
2.观察图中所示的长方体,完成填空:
(1)用符号表示下列两棱所在直线的位置关系:
HD
GC,FB
AB;
(2)AD和GC所在直线
(填“是”或“不是”)平行线,理由是
.
巩固所学新知.
11
同课章节目录
- 第一章 有理数
- 1.1 负数的引入
- 1.2 用数轴上的点表示有理数
- 1.3 相反数和绝对值
- 1.4 有理数的加法
- 1.5 有理数的减法
- 1.6 有理数加减法的混合运算
- 1.7 有理数的乘法
- 1.8 有理数的除法
- 1.9 有理数的乘方
- 1.10 有理数的混合运算
- 1.11 数的近似和科学记数法
- 1.12 用计算器做有理数的混合运算
- 第二章 一元一次方程
- 2.1 字母表示数
- 2.2 同类项与合并同类项
- 2.3 等式与方程
- 2.4 等式的基本性质
- 2.5 一元一次方程
- 2.6 列方程解应用问题
- 第三章 简单的几何图形
- 3.1 平面图形与立体图形
- 3.2 某些立体图形的展开图
- 3.3 从不同方向观察立体图形
- 3.4 点、线、面、体
- 3.5 直线、射线、线段
- 3.6 角及其分类
- 3.7 角的度量与角的换算
- 3.8 角平分线
- 3.9 两条直线的位置关系
- 3.10 相交线与平行线
- 3.11 用计算机绘图
