2020-2021学年数学人教A版(2019)必修第二册直线、平面平行的判定及其性质复习课课件(共20张PPT)
文档属性
| 名称 | 2020-2021学年数学人教A版(2019)必修第二册直线、平面平行的判定及其性质复习课课件(共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 786.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-08 21:55:12 | ||
图片预览





文档简介
(共20张PPT)
直线、平面平行的判定及其性质(复习课)
Line,Plane
Parallel
Judgment
and
Properties(Review)
问题1
若直线
与平面
内的一条直线平行,则
?
问题2
若平面
内有两条直线分别与平面
平行,则
?
问题3
若直线
与平面
平行,则
与平面
内的任意一条直线都平行?
问题4
若平面
与平面
平行,则平面
内的任意一条直线与平面
都平行?
问题5
若一个平面和两个平行平面同时相交,则它们的交线平行?
一、思考辨析(Think
about)
问题1(Question
1)
若直线
与平面
内的一条直线平行,则
?
直线与平面平行的判定定理
若平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行.
一、思考辨析(Think
about)
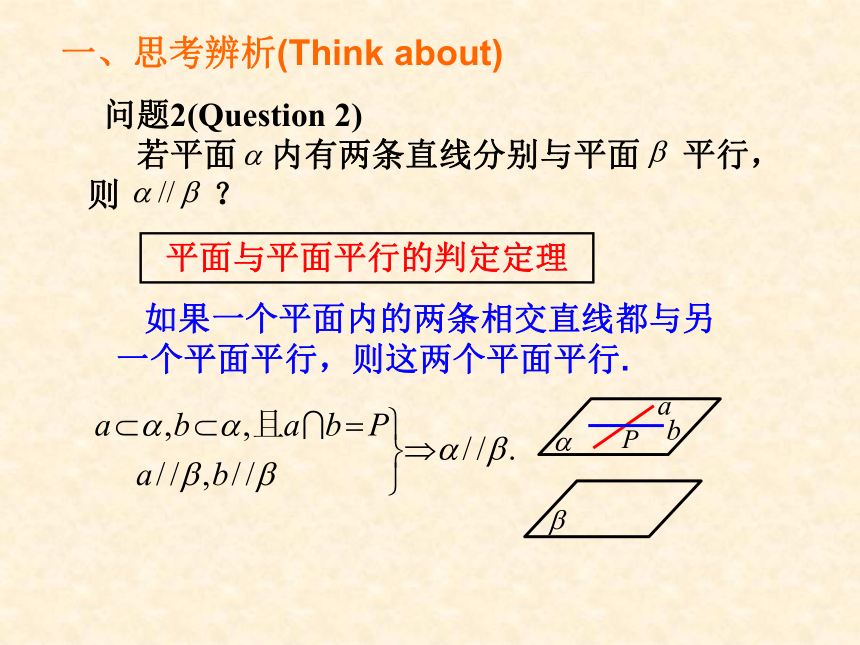
问题2(Question
2)
若平面
内有两条直线分别与平面
平行,则
?
平面与平面平行的判定定理
如果一个平面内的两条相交直线都与另一个平面平行,则这两个平面平行.
一、思考辨析(Think
about)
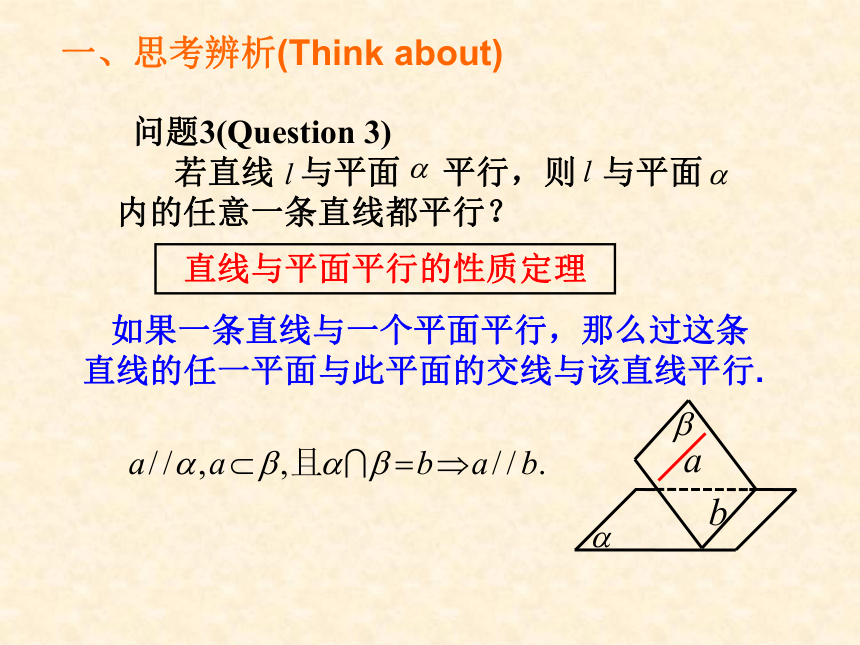
问题3(Question
3)
若直线
与平面
平行,则
与平面
内的任意一条直线都平行?
直线与平面平行的性质定理
如果一条直线与一个平面平行,那么过这条直线的任一平面与此平面的交线与该直线平行.
一、思考辨析(Think
about)
问题4(Question
4)
若平面
与平面
平行,则平面
内的任意一条直线与平面
都平行?
平面与平面平行的性质定理
如果两个平面平行,那么其中一个平面内的任意一条直线必平行另一个平面.
一、思考辨析(Think
about)
问题5(Question
5)
若一个平面和两个平行平面同时相交,则它们的交线平行?
平面与平面平行的性质定理
如果两个平行平面同时和第三个平面
相交,那么它们的交线平行.
一、思考辨析(Think
about)
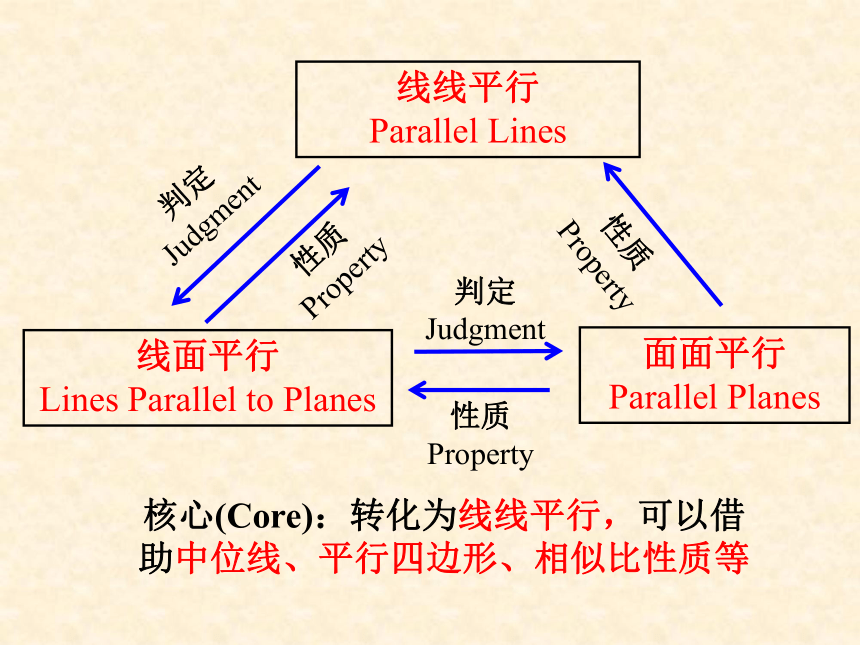
判定
Judgment
核心(Core):转化为线线平行,可以借助中位线、平行四边形、相似比性质等
线面平行
Lines
Parallel
to
Planes
性质
Property
线线平行
Parallel
Lines
面面平行
Parallel
Planes
判定
Judgment
性质
Property
性质
Property
(一)典例剖析(Analysis
of
Typical
Examples)
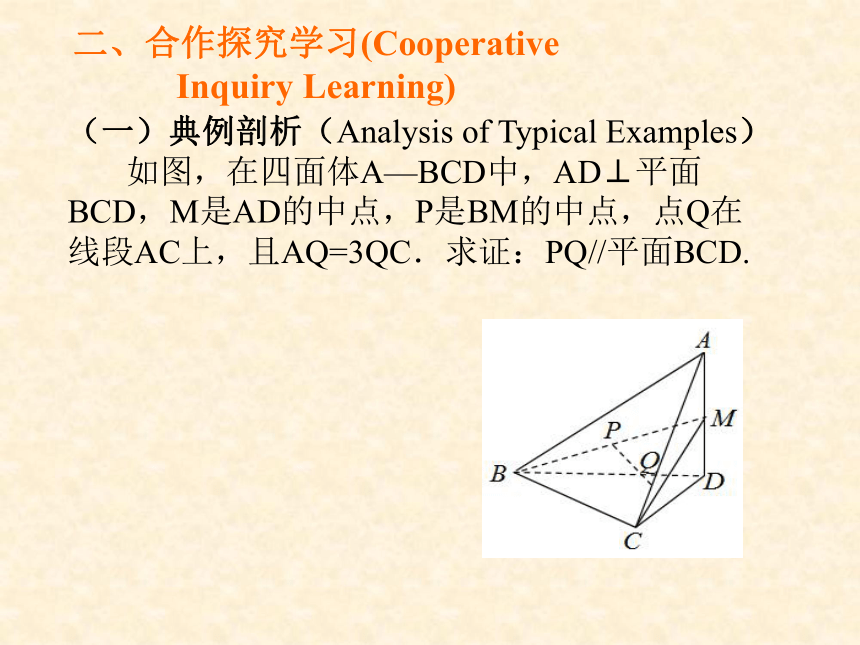
如图,在四面体A—BCD中,AD⊥平面BCD,M是AD的中点,P是BM的中点,点Q在线段AC上,且AQ=3QC.求证:PQ//平面BCD.
二、合作探究学习(Cooperative
Inquiry
Learning)
证法一(Proof
1)
(思路点拨)
取MD边的中点记为E,连接PE,QE,易得
平面PQE//平面BCD,进而推出PQ//平面BCD.
利用相似比性质,推出面面平行,进而推出线面平行
证法二(Proof
2)(思路点拨)
取CD边上的一点记为E,使DE=3CE,取BD边的中点记为F,连接PF,易得四边形EFPQ为平行四边形,进而推出PQ//平面BCD.
构造平行四边形,推出线线平行,进而推出线面平行
证法三(Proof
3)(思路点拨)
连接AP并延长交BD于点E,由相似比性质,易得PQ//EC,进而推出PQ//平面BCD.
利用相似比性质,推出线线平行,进而推出线面平行
§方法小结(Summary)
证明直线、平面平行的关键是把问题转化为“线线平行”,这可以结合几何体的特征,合理利用中位线定理、构造平行四边形、寻找比例式等方法来证明两直线平行.
(二)拓展延伸(Extension)
如图,在四棱锥P—ABCD中,底面ABCD是平行四边形,E是PC的中点,在DE上取一点F,过F和AP作平面交平面BDE于FG,求证FG//AP.
二、合作探究学习(Cooperative
Inquiry
Learning)
证法(Proof)
(思路点拨)
连接AC交BD于点O,连接EO,易得EO//平面PAC,再由线面平行的性质,推出FG//AP.
利用中位线性质,推出线面平行,结合线面平行的性质,进而推出线线平行
§方法小结(Summary)
在寻找直线、平面平行关系时,应注意性质定理的应用,同时应注意交线位置的确定,有时需要过已知直线作辅助平面来确定交线.
线面平行的证明方法有哪些?应注意些什么?面面平行呢?
三、总结与回顾(Summary
and
Review)
完成学案课后作业!
四、作业(Homework)
成长路上,一路相随!
We
will
always
be
with
you!
感谢大家聆听!
Thank
You!
直线、平面平行的判定及其性质(复习课)
Line,Plane
Parallel
Judgment
and
Properties(Review)
问题1
若直线
与平面
内的一条直线平行,则
?
问题2
若平面
内有两条直线分别与平面
平行,则
?
问题3
若直线
与平面
平行,则
与平面
内的任意一条直线都平行?
问题4
若平面
与平面
平行,则平面
内的任意一条直线与平面
都平行?
问题5
若一个平面和两个平行平面同时相交,则它们的交线平行?
一、思考辨析(Think
about)
问题1(Question
1)
若直线
与平面
内的一条直线平行,则
?
直线与平面平行的判定定理
若平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行.
一、思考辨析(Think
about)
问题2(Question
2)
若平面
内有两条直线分别与平面
平行,则
?
平面与平面平行的判定定理
如果一个平面内的两条相交直线都与另一个平面平行,则这两个平面平行.
一、思考辨析(Think
about)
问题3(Question
3)
若直线
与平面
平行,则
与平面
内的任意一条直线都平行?
直线与平面平行的性质定理
如果一条直线与一个平面平行,那么过这条直线的任一平面与此平面的交线与该直线平行.
一、思考辨析(Think
about)
问题4(Question
4)
若平面
与平面
平行,则平面
内的任意一条直线与平面
都平行?
平面与平面平行的性质定理
如果两个平面平行,那么其中一个平面内的任意一条直线必平行另一个平面.
一、思考辨析(Think
about)
问题5(Question
5)
若一个平面和两个平行平面同时相交,则它们的交线平行?
平面与平面平行的性质定理
如果两个平行平面同时和第三个平面
相交,那么它们的交线平行.
一、思考辨析(Think
about)
判定
Judgment
核心(Core):转化为线线平行,可以借助中位线、平行四边形、相似比性质等
线面平行
Lines
Parallel
to
Planes
性质
Property
线线平行
Parallel
Lines
面面平行
Parallel
Planes
判定
Judgment
性质
Property
性质
Property
(一)典例剖析(Analysis
of
Typical
Examples)
如图,在四面体A—BCD中,AD⊥平面BCD,M是AD的中点,P是BM的中点,点Q在线段AC上,且AQ=3QC.求证:PQ//平面BCD.
二、合作探究学习(Cooperative
Inquiry
Learning)
证法一(Proof
1)
(思路点拨)
取MD边的中点记为E,连接PE,QE,易得
平面PQE//平面BCD,进而推出PQ//平面BCD.
利用相似比性质,推出面面平行,进而推出线面平行
证法二(Proof
2)(思路点拨)
取CD边上的一点记为E,使DE=3CE,取BD边的中点记为F,连接PF,易得四边形EFPQ为平行四边形,进而推出PQ//平面BCD.
构造平行四边形,推出线线平行,进而推出线面平行
证法三(Proof
3)(思路点拨)
连接AP并延长交BD于点E,由相似比性质,易得PQ//EC,进而推出PQ//平面BCD.
利用相似比性质,推出线线平行,进而推出线面平行
§方法小结(Summary)
证明直线、平面平行的关键是把问题转化为“线线平行”,这可以结合几何体的特征,合理利用中位线定理、构造平行四边形、寻找比例式等方法来证明两直线平行.
(二)拓展延伸(Extension)
如图,在四棱锥P—ABCD中,底面ABCD是平行四边形,E是PC的中点,在DE上取一点F,过F和AP作平面交平面BDE于FG,求证FG//AP.
二、合作探究学习(Cooperative
Inquiry
Learning)
证法(Proof)
(思路点拨)
连接AC交BD于点O,连接EO,易得EO//平面PAC,再由线面平行的性质,推出FG//AP.
利用中位线性质,推出线面平行,结合线面平行的性质,进而推出线线平行
§方法小结(Summary)
在寻找直线、平面平行关系时,应注意性质定理的应用,同时应注意交线位置的确定,有时需要过已知直线作辅助平面来确定交线.
线面平行的证明方法有哪些?应注意些什么?面面平行呢?
三、总结与回顾(Summary
and
Review)
完成学案课后作业!
四、作业(Homework)
成长路上,一路相随!
We
will
always
be
with
you!
感谢大家聆听!
Thank
You!
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
