沪教版(上海)高一数学上册 2.4基本不等式及其应用_1 课件(共20张PPT)
文档属性
| 名称 | 沪教版(上海)高一数学上册 2.4基本不等式及其应用_1 课件(共20张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 647.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-09 09:05:24 | ||
图片预览








文档简介
(共20张PPT)
基本不等式及其应用
知识与技能
1.
掌握两个基本不等式,并能运用它们解决简单的问题。
2.理解两个不等式的几何意义,并能适当地变形运用它们。
过程与方法
1.通过公式探求过程的学习,体验数学发现的重要意义。
2.通过对变换方法与技巧的学习,领悟转化思想在学习中
存在的普遍价值。
情感态度与价值观
通过最值的学习,深入了解数学在实际生活中的重要价值,
以及数学对经济学的深远影响,提高学习数学的兴趣。
〔教学目标〕
1.
重点掌握两个基本不等式发现的探索过程和应用它们求相关最值。
2.
难点是两个基本不等式的几何意义和变形运用求最值。
3.
在运用基本不等式2求最值时,要注意一正、二定、三等。
4.
在多次使用不等式求最值时,要注意等号成立的条件是否一致。
〔学习要求
〕
这是2002年数学大会的会徽,你们能想象到吗?它与我国数学史却有着深厚的情源?
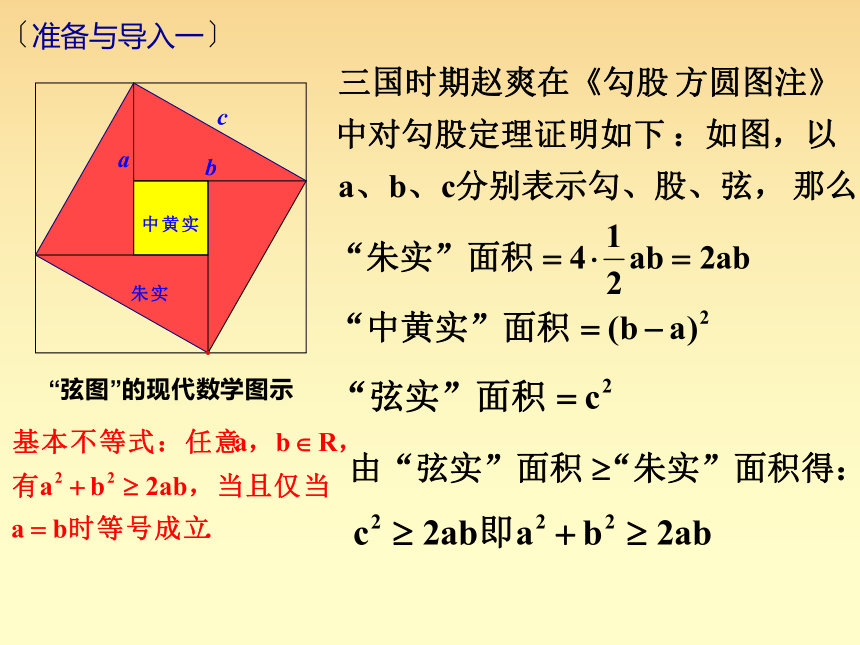
〔准备与导入一〕
首先,请观察图案
〔准备与导入一〕
问题:你能用代数方法证明这两个不等式吗?
〔探究与深化一〕
综上我们发现了两个非常重要的基本不等式:
算术平均数
几何平均数
〔探究与深化一〕
基本不等式1
证明:
注:基本不等式2的证明请学生完成,
并处理本节课开始的围建鸭舍问题。
问题:比较这两个基本不等式,你发现了
它们之间的联系了吗?
从条件上分析
从结构上分析
〔探究与深化一〕
例1.
〔探究与深化一〕
问题:本题能直接用不等式求最值吗?
应补上什么条件?
应选择哪个基本不等式?
等号成立的条件不可少
一正、二定、三等
例2.
〔探究与深化一〕
问题:若把例1中的条件x>1去掉,还有
最小值吗?哪可改为求什么呢?
〔探究与深化一〕
注:1.两个正数的积为定值时,它们
的和有最小值。积定和小。
2.不可忽视等号成立的条件。
答案:错在等号成立的条件不存在。
注:1.两个正数的和为定值时,它们的积
有最大值。和定积大。
2.不可忽视等号成立的条件。
〔探究与深化一〕
〔探究与深化一〕
例5.当x取什么值时,代数式
取最大值?并求出这个最大值.
所以,原代数式的最大值为1/2.
〔回顾与小结〕
本节课研究了两个恒不等式
初步应用两个基本不等式求最值。
〔练习与评价一〕
〔练习与评价一〕
〔作业与拓展一〕
〔作业与拓展一〕
基本不等式及其应用
知识与技能
1.
掌握两个基本不等式,并能运用它们解决简单的问题。
2.理解两个不等式的几何意义,并能适当地变形运用它们。
过程与方法
1.通过公式探求过程的学习,体验数学发现的重要意义。
2.通过对变换方法与技巧的学习,领悟转化思想在学习中
存在的普遍价值。
情感态度与价值观
通过最值的学习,深入了解数学在实际生活中的重要价值,
以及数学对经济学的深远影响,提高学习数学的兴趣。
〔教学目标〕
1.
重点掌握两个基本不等式发现的探索过程和应用它们求相关最值。
2.
难点是两个基本不等式的几何意义和变形运用求最值。
3.
在运用基本不等式2求最值时,要注意一正、二定、三等。
4.
在多次使用不等式求最值时,要注意等号成立的条件是否一致。
〔学习要求
〕
这是2002年数学大会的会徽,你们能想象到吗?它与我国数学史却有着深厚的情源?
〔准备与导入一〕
首先,请观察图案
〔准备与导入一〕
问题:你能用代数方法证明这两个不等式吗?
〔探究与深化一〕
综上我们发现了两个非常重要的基本不等式:
算术平均数
几何平均数
〔探究与深化一〕
基本不等式1
证明:
注:基本不等式2的证明请学生完成,
并处理本节课开始的围建鸭舍问题。
问题:比较这两个基本不等式,你发现了
它们之间的联系了吗?
从条件上分析
从结构上分析
〔探究与深化一〕
例1.
〔探究与深化一〕
问题:本题能直接用不等式求最值吗?
应补上什么条件?
应选择哪个基本不等式?
等号成立的条件不可少
一正、二定、三等
例2.
〔探究与深化一〕
问题:若把例1中的条件x>1去掉,还有
最小值吗?哪可改为求什么呢?
〔探究与深化一〕
注:1.两个正数的积为定值时,它们
的和有最小值。积定和小。
2.不可忽视等号成立的条件。
答案:错在等号成立的条件不存在。
注:1.两个正数的和为定值时,它们的积
有最大值。和定积大。
2.不可忽视等号成立的条件。
〔探究与深化一〕
〔探究与深化一〕
例5.当x取什么值时,代数式
取最大值?并求出这个最大值.
所以,原代数式的最大值为1/2.
〔回顾与小结〕
本节课研究了两个恒不等式
初步应用两个基本不等式求最值。
〔练习与评价一〕
〔练习与评价一〕
〔作业与拓展一〕
〔作业与拓展一〕
