沪教版(上海)高一数学上册 4.2 《指数函数的图像和性质》 教案(Word表格式)
文档属性
| 名称 | 沪教版(上海)高一数学上册 4.2 《指数函数的图像和性质》 教案(Word表格式) |

|
|
| 格式 | doc | ||
| 文件大小 | 258.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-09 09:43:03 | ||
图片预览


文档简介
高一数学上册
《指数函数的图像和性质》
教学设计
教学基本信息
课题
指数函数的图像和性质
授课人
授课时间
授课班级
授课教材
沪教版高一数学上册《指数函数的图像和性质》模块
教学背景分析
教材分析:《指数函数》是高中生在学习了函数的概念及性质后,研究的第一个基本初等函数.它的研究,一方面可以进一步深化学生对第三章《函数的基本性质》的相关知识和思想方法的理解,另一方面也为研究对数函数、幂函数、三角函数等基本初等函数打下基础.本节课的教学内容是指数函数及其性质.教材首先通过实际情境的设置,让学生从实际问题中抽象概括出指数函数的概念;然后从具体的指数函数出发,经过列表、描点、连线的作图过程,画出图像;接着,通过观察图像,从中感悟并归纳出指数函数的性质,这是本节课的一条明线;在探索指数函数性质的过程中,学生体验了研究函数的基本方法,是本节课的一条暗线,也是今后研究其他函数的主线.学情分析:在基本知识上,学生已经较系统地学习了函数的概念及其性质,并完成了指数取值范围的扩充,习得指数幂的运算法则.在基本技能上,学生能借助列表、描点的方法作图,通过观察图象,获得对函数基本性质的直观认识.在基本思想方法上,学生通过第三章函数的研究,形成了一定的数形结合、分类讨论、特殊与一般、归纳的思想方法。在基本活动经验上,学生通过第三章《函数的基本性质》的学习,体验了函数及其性质、一次函数和二次函数的研究过程,给本节课的自主探究积累了经验。
同时,集合概念和函数概念的抽象过程以及函数应用的学习,促使学生经历了从数学角度发现问题、提出问题、分析问题及解决问题的过程,提高了相应的能力。因此本节课通过遵循教材分析中的“明线”来研究指数概念的想法较易实现。然而,学生思维的严谨性、活跃性以及分类讨论、归纳推理等能力有待提高。
教学目标及重难点分析
教学目标:
通过具体事例,了解指数函数的实际意义,理解指数函数的概念。能用描点法画出具体指数函数的图象,探索并理解指数函数的单调性和特殊点,体会数学内容之间的联系,提升并发展数学抽象素养、直观想象素养、逻辑推理素养。教学重点:
指数函数定义、图象、性质及其简单应用。教学难点:指数函数图像和性质的发现、总结过程。
教学设计思想
首先从两个实际问题出发,抽象出指数函数的概念,同时激发学生的学习兴趣。指数函数概念的理解重在对底数取值范围的讨论;然后,对指数函数性质的学习分成两个部分。一是对特殊的指数函数进行探究,利用坐标纸,小组通过分工合作,在同一坐标系中做出不同底数的指数函数图像,借助多媒体,展示小组作品,引导学生发现底互为倒数的两指数函数图象间的对称关系;二是激发学生采用特殊到一般的思想方法,启发他们把特殊的指数函数按底数划分为01两种类型,并给出一般指数函数的性质。
教学过程
教学方式:问题引导,学生探究交流。学生经历观察、分析、归纳、抽象、概况、探究过程,采取合作交流的学习方法,借助多媒体调动学生学习积极性。教学手段:幻灯片、投影仪、几何画板技术准备:演示文稿、指数函坐标纸具体过程:
教学过程
学生活动
设计意图
创设情境
通过第二章的学习,我们了解了函数的概念及其性质,并初步体会了研究函数的一般过程与方法,本节课我们将在前几节课学习的基础上,研究新的函数。首先,先看两个具体的实际问题,研究问题中两个变量之间的依赖关系.情境1:细胞分裂问题某个细胞第一次分裂,1个分裂为2个;第二次分裂,2个分裂为4个,……,这样下去,第10次,分裂后共有多少个细胞?第x次呢?得到细胞个数y与分裂次数x之间的关系式:y=2x情境2:
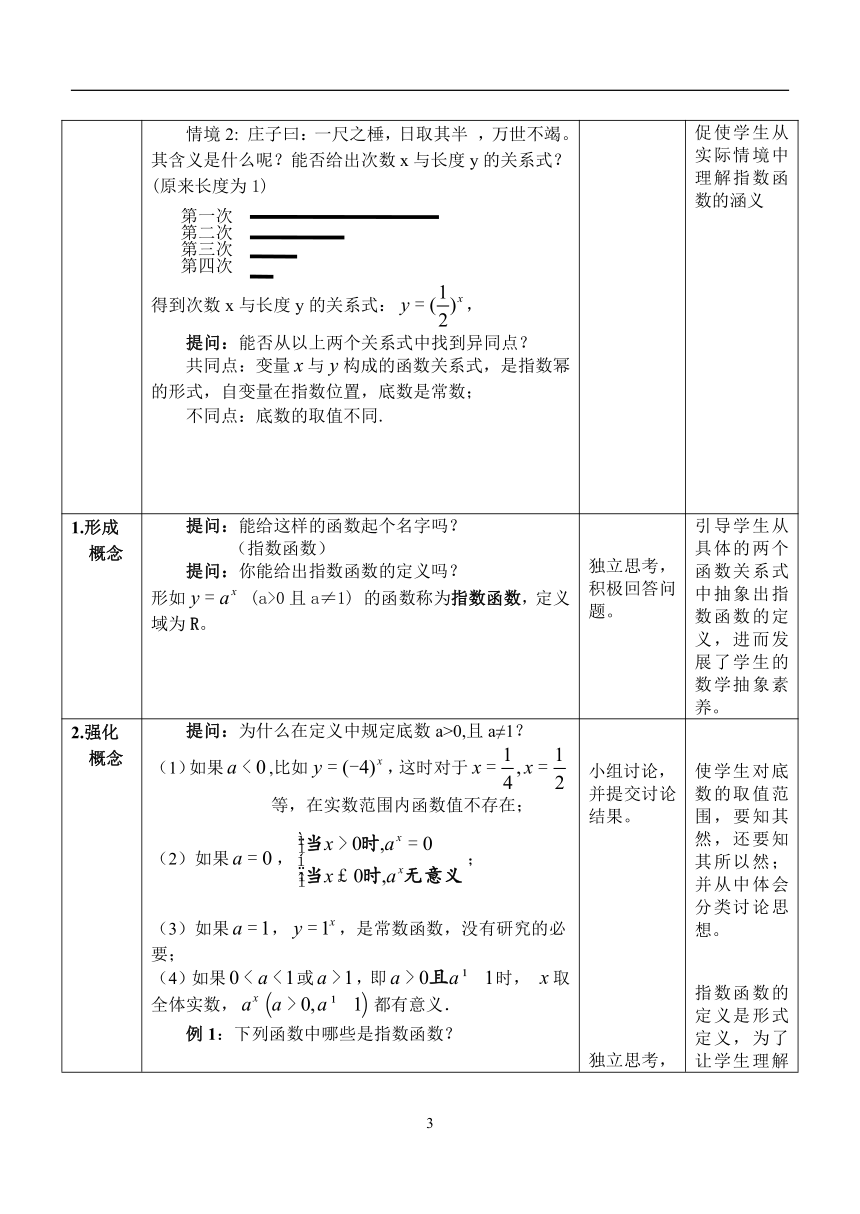
庄子曰:一尺之棰,日取其半
,万世不竭。其含义是什么呢?能否给出次数x与长度y的关系式?(原来长度为1)
得到次数x与长度y的关系式:,提问:能否从以上两个关系式中找到异同点?
共同点:变量与构成的函数关系式,是指数幂的形式,自变量在指数位置,底数是常数;不同点:底数的取值不同.
积极思考,回答问题。
引起学生学习兴趣。促使学生从实际情境中理解指数函数的涵义
1.形成概念
提问:能给这样的函数起个名字吗?(指数函数)
提问:你能给出指数函数的定义吗?形如?(a>0且a≠1)
的函数称为指数函数,定义域为R。
独立思考,积极回答问题。
引导学生从具体的两个函数关系式中抽象出指数函数的定义,进而发展了学生的数学抽象素养。
2.强化概念
提问:为什么在定义中规定底数a>0,且a≠1?(1)如果,比如,这时对于等,在实数范围内函数值不存在;(2)如果,;(3)如果,,是常数函数,没有研究的必要;(4)如果或,即时,
取全体实数,都有意义.例1:下列函数中哪些是指数函数?(1)(2)
(3)
(4)(5)解析:指数函数的定义是形式定义,就必须在形式上一模一样,进而得出只有(1)、(5)是指数函数。
小组讨论,并提交讨论结果。独立思考,并积极回答问题.
使学生对底数的取值范围,要知其然,还要知其所以然;并从中体会分类讨论思想。指数函数的定义是形式定义,为了让学生理解这种形式定义,设置了该问题.
3.探究新知
提问:我们要研究一个函数,光有定义是远远不够的,还要研究什么,如何研究呢?还有函数的图像、性质及应用.一般以函数图象为载体研究函数性质,用图象和性质解决实际问题。所以,下一个要研究的问题就是——指数函数图象小组活动:①每个小组发放一份统一印制有坐标系的绘图纸。②设计4组指数函数:(1)y=2x和;(2)y=3x和;(3)y=2x,y=3x
(4),。制成8张小卡片,每张小卡片上只有一组指数函数(每一组都出现两次),装入信封,由8位小组负责人各抽取一份,要求学生以小组合作的方式,画出它们的图象,根据图像,请给出它们的性质。y=2xy=3x定义域值域是否过定点奇偶性单调性提问:
通过这几组指数函数的研究,你能得出什么结论?请将你的研究结论填入下表,自主完善表格。分类 a>1 00时,
当x<0时,
当x>0时,
当x<0时,
奇偶性 单调性
独立思考,并积极回答教师问题
小组合作探究,用描点法画出4组函数图像,通过观察图像,交流讨论,给出研究发现
重在学生的体验,让学生经过小组合作、自主探究的过程,加深对指数函数图像的认识,从图像中深入理解指数函数的性质,同时积累了研究函数的经验,该探究过程同时也发展了学生的逻辑推理素养及直观想象素养.
4.巩固提高
(可由老师根据课堂所剩时间,灵活选择.)例2、已知指数函数f(x)的图象过点(3,8),比较f(0),
f(1),
f(-3)的大小.例3、(1)函数y=(a2-1)x在R上为增函数,则求a的取值范围.
(2)若函数y=(a2-3a+a)ax是指数函数,求a的值.练习:利用指数函数的性质,比较下列各题中两个值的大小.①30.8与30.7
②0.750.1与0.75-0.
1③0.8-0.1与1.250.2
④0.250.8与0.51.8
学生先独立思考,尝试解决问题,然后规范格式之后再解决.
学生练习
实现学生对指数函数知识的初步应用,让学生体会“实践―认识―再实践”的学习过程。
课后思考
1、本节课学习的主要内容有:
;2、本节课使用的主要数学思想有:
;
学生回顾反思
引导学生对指数函数的知识进行梳理,利于学生系统掌握所学内容,深化知识与技能。
板书设计
4.2
指数函数的图像和性质1.定义:一般地,形如?(a>0且a≠1)
的函数称为指数函数,定义域为R2.图像
a>1
00,即值域是;(2)函数图像在x轴的上方且都过点(0,1);(3)当a>1时,这个函数是增函数;
当0课后反思
1.数学知识在本节探究指数函数图像及性质时,除了引导学生观察指数函数定义域、值域、奇偶性和单调性等一般性质,还应引导学生观察底数与图像的关系:(1)当a>1时,a的值越大,图像就越靠近y轴,递增速度越来越快;
当0在y轴左侧,图像从下到上相应的底数由大变小;2.数学思想本节课在研究指数函数时主要采用了数形结合思想中的“形”
“数”,事实上,如果能结合“数”
“形”,就更能体现出数学的严谨.从这个角度出发,可将学生分为两大组,其中一组从“形”到“数”自主探究指数函数的图像和性质,另外一组,从“数”到“形”探究.3.数学核心素养的培养依据数学教育的理论,数学核心素养的培养可通过教学生“思考”、
教学生“体验”及教学生“表达”来实现。本节课在研究指数函数的过程中关注了学生的思考和体验,然而却忽视了学生的表达,即学生自己表达整个探究过程及结果。4.专业素养及评价在本节课的授课过程中,虽然我的语言精练,但是声音略小,板书规范却不漂亮.同时,在评价学生的回答时,只关注了我的评价,却忽视了学生自己的评价,以及同学们的评价.面对这些不足,我应尽快提高自己的基本素养及课堂评价方式.
第一次
第二次
第三次
第四次
PAGE
6
《指数函数的图像和性质》
教学设计
教学基本信息
课题
指数函数的图像和性质
授课人
授课时间
授课班级
授课教材
沪教版高一数学上册《指数函数的图像和性质》模块
教学背景分析
教材分析:《指数函数》是高中生在学习了函数的概念及性质后,研究的第一个基本初等函数.它的研究,一方面可以进一步深化学生对第三章《函数的基本性质》的相关知识和思想方法的理解,另一方面也为研究对数函数、幂函数、三角函数等基本初等函数打下基础.本节课的教学内容是指数函数及其性质.教材首先通过实际情境的设置,让学生从实际问题中抽象概括出指数函数的概念;然后从具体的指数函数出发,经过列表、描点、连线的作图过程,画出图像;接着,通过观察图像,从中感悟并归纳出指数函数的性质,这是本节课的一条明线;在探索指数函数性质的过程中,学生体验了研究函数的基本方法,是本节课的一条暗线,也是今后研究其他函数的主线.学情分析:在基本知识上,学生已经较系统地学习了函数的概念及其性质,并完成了指数取值范围的扩充,习得指数幂的运算法则.在基本技能上,学生能借助列表、描点的方法作图,通过观察图象,获得对函数基本性质的直观认识.在基本思想方法上,学生通过第三章函数的研究,形成了一定的数形结合、分类讨论、特殊与一般、归纳的思想方法。在基本活动经验上,学生通过第三章《函数的基本性质》的学习,体验了函数及其性质、一次函数和二次函数的研究过程,给本节课的自主探究积累了经验。
同时,集合概念和函数概念的抽象过程以及函数应用的学习,促使学生经历了从数学角度发现问题、提出问题、分析问题及解决问题的过程,提高了相应的能力。因此本节课通过遵循教材分析中的“明线”来研究指数概念的想法较易实现。然而,学生思维的严谨性、活跃性以及分类讨论、归纳推理等能力有待提高。
教学目标及重难点分析
教学目标:
通过具体事例,了解指数函数的实际意义,理解指数函数的概念。能用描点法画出具体指数函数的图象,探索并理解指数函数的单调性和特殊点,体会数学内容之间的联系,提升并发展数学抽象素养、直观想象素养、逻辑推理素养。教学重点:
指数函数定义、图象、性质及其简单应用。教学难点:指数函数图像和性质的发现、总结过程。
教学设计思想
首先从两个实际问题出发,抽象出指数函数的概念,同时激发学生的学习兴趣。指数函数概念的理解重在对底数取值范围的讨论;然后,对指数函数性质的学习分成两个部分。一是对特殊的指数函数进行探究,利用坐标纸,小组通过分工合作,在同一坐标系中做出不同底数的指数函数图像,借助多媒体,展示小组作品,引导学生发现底互为倒数的两指数函数图象间的对称关系;二是激发学生采用特殊到一般的思想方法,启发他们把特殊的指数函数按底数划分为0
教学过程
教学方式:问题引导,学生探究交流。学生经历观察、分析、归纳、抽象、概况、探究过程,采取合作交流的学习方法,借助多媒体调动学生学习积极性。教学手段:幻灯片、投影仪、几何画板技术准备:演示文稿、指数函坐标纸具体过程:
教学过程
学生活动
设计意图
创设情境
通过第二章的学习,我们了解了函数的概念及其性质,并初步体会了研究函数的一般过程与方法,本节课我们将在前几节课学习的基础上,研究新的函数。首先,先看两个具体的实际问题,研究问题中两个变量之间的依赖关系.情境1:细胞分裂问题某个细胞第一次分裂,1个分裂为2个;第二次分裂,2个分裂为4个,……,这样下去,第10次,分裂后共有多少个细胞?第x次呢?得到细胞个数y与分裂次数x之间的关系式:y=2x情境2:
庄子曰:一尺之棰,日取其半
,万世不竭。其含义是什么呢?能否给出次数x与长度y的关系式?(原来长度为1)
得到次数x与长度y的关系式:,提问:能否从以上两个关系式中找到异同点?
共同点:变量与构成的函数关系式,是指数幂的形式,自变量在指数位置,底数是常数;不同点:底数的取值不同.
积极思考,回答问题。
引起学生学习兴趣。促使学生从实际情境中理解指数函数的涵义
1.形成概念
提问:能给这样的函数起个名字吗?(指数函数)
提问:你能给出指数函数的定义吗?形如?(a>0且a≠1)
的函数称为指数函数,定义域为R。
独立思考,积极回答问题。
引导学生从具体的两个函数关系式中抽象出指数函数的定义,进而发展了学生的数学抽象素养。
2.强化概念
提问:为什么在定义中规定底数a>0,且a≠1?(1)如果,比如,这时对于等,在实数范围内函数值不存在;(2)如果,;(3)如果,,是常数函数,没有研究的必要;(4)如果或,即时,
取全体实数,都有意义.例1:下列函数中哪些是指数函数?(1)(2)
(3)
(4)(5)解析:指数函数的定义是形式定义,就必须在形式上一模一样,进而得出只有(1)、(5)是指数函数。
小组讨论,并提交讨论结果。独立思考,并积极回答问题.
使学生对底数的取值范围,要知其然,还要知其所以然;并从中体会分类讨论思想。指数函数的定义是形式定义,为了让学生理解这种形式定义,设置了该问题.
3.探究新知
提问:我们要研究一个函数,光有定义是远远不够的,还要研究什么,如何研究呢?还有函数的图像、性质及应用.一般以函数图象为载体研究函数性质,用图象和性质解决实际问题。所以,下一个要研究的问题就是——指数函数图象小组活动:①每个小组发放一份统一印制有坐标系的绘图纸。②设计4组指数函数:(1)y=2x和;(2)y=3x和;(3)y=2x,y=3x
(4),。制成8张小卡片,每张小卡片上只有一组指数函数(每一组都出现两次),装入信封,由8位小组负责人各抽取一份,要求学生以小组合作的方式,画出它们的图象,根据图像,请给出它们的性质。y=2xy=3x定义域值域是否过定点奇偶性单调性提问:
通过这几组指数函数的研究,你能得出什么结论?请将你的研究结论填入下表,自主完善表格。分类 a>1 0
当x<0时,
当x>0时,
当x<0时,
奇偶性 单调性
独立思考,并积极回答教师问题
小组合作探究,用描点法画出4组函数图像,通过观察图像,交流讨论,给出研究发现
重在学生的体验,让学生经过小组合作、自主探究的过程,加深对指数函数图像的认识,从图像中深入理解指数函数的性质,同时积累了研究函数的经验,该探究过程同时也发展了学生的逻辑推理素养及直观想象素养.
4.巩固提高
(可由老师根据课堂所剩时间,灵活选择.)例2、已知指数函数f(x)的图象过点(3,8),比较f(0),
f(1),
f(-3)的大小.例3、(1)函数y=(a2-1)x在R上为增函数,则求a的取值范围.
(2)若函数y=(a2-3a+a)ax是指数函数,求a的值.练习:利用指数函数的性质,比较下列各题中两个值的大小.①30.8与30.7
②0.750.1与0.75-0.
1③0.8-0.1与1.250.2
④0.250.8与0.51.8
学生先独立思考,尝试解决问题,然后规范格式之后再解决.
学生练习
实现学生对指数函数知识的初步应用,让学生体会“实践―认识―再实践”的学习过程。
课后思考
1、本节课学习的主要内容有:
;2、本节课使用的主要数学思想有:
;
学生回顾反思
引导学生对指数函数的知识进行梳理,利于学生系统掌握所学内容,深化知识与技能。
板书设计
4.2
指数函数的图像和性质1.定义:一般地,形如?(a>0且a≠1)
的函数称为指数函数,定义域为R2.图像
a>1
0
当0
1.数学知识在本节探究指数函数图像及性质时,除了引导学生观察指数函数定义域、值域、奇偶性和单调性等一般性质,还应引导学生观察底数与图像的关系:(1)当a>1时,a的值越大,图像就越靠近y轴,递增速度越来越快;
当0
“数”,事实上,如果能结合“数”
“形”,就更能体现出数学的严谨.从这个角度出发,可将学生分为两大组,其中一组从“形”到“数”自主探究指数函数的图像和性质,另外一组,从“数”到“形”探究.3.数学核心素养的培养依据数学教育的理论,数学核心素养的培养可通过教学生“思考”、
教学生“体验”及教学生“表达”来实现。本节课在研究指数函数的过程中关注了学生的思考和体验,然而却忽视了学生的表达,即学生自己表达整个探究过程及结果。4.专业素养及评价在本节课的授课过程中,虽然我的语言精练,但是声音略小,板书规范却不漂亮.同时,在评价学生的回答时,只关注了我的评价,却忽视了学生自己的评价,以及同学们的评价.面对这些不足,我应尽快提高自己的基本素养及课堂评价方式.
第一次
第二次
第三次
第四次
PAGE
6
