沪教版(上海)高一数学上册 3.2 函数关系的建立 教案
文档属性
| 名称 | 沪教版(上海)高一数学上册 3.2 函数关系的建立 教案 |

|
|
| 格式 | docx | ||
| 文件大小 | 187.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-09 09:33:32 | ||
图片预览


文档简介
函数关系的建立——绝对值和函数模型的建立与运用
教学目标
理解绝对值和函数的几何意义,归纳概括绝对值和函数最值的数学模型.
利用绝对值和函数最值的数学模型,运用化归的思想方法,解决相关问题.
通过创设情境,初步形成自主研究数学问题的能力,养成层层递进地思考数学问题的习惯,体验突破困难取得成功的喜悦.
教学重点:
绝对值和函数性质的探究与其最值数学模型的建模过程.
教学难点:
运用绝对值和函数最值的数学模型解决相关问题.
教学过程:
一、引入课题
我们在作业中遇到过这样一道高考题:
引例(1)(2014安徽)若函数的最小值为,则的值_______.
(解法一)分类讨论、零点分段
当a≥2时,f(x)=
当a<2时,f(x)=
综上可知,a的值为-4或8.
(解法二)几何意义:距离之和
根据绝对值的几何意义,此函数可看做是数轴上一点到的距离与到距离的两倍之和,显然,当介于与之间时,为定值,只需使剩下的取到最小值0时,函数值最小.因此
.a的值为-4或8.
解法一是绝对值和函数问题的常规解法,不过解法二更加高效简洁,形象生动.将上述例题看作是3个绝对值相加的问题,那么如果改变题中绝对值的个数,如4个、5个……绝对值相加,问题的情形会发生哪些变化,它们的一般情况是什么样的呢?今天我们就这个问题做一个深入的探究.
二、模型建立
我们把形如,其中,
的函数称作绝对值和函数.根据绝对值的几何意义,在其定义域上没有最大值,而有最小值,并且最小值处的自变量取值与函数中绝对值的零点有关.
问题分析:类似于例题的情况,当奇数个绝对值相加时,函数的几何意义为数轴上的一点到个零点的距离之和.
显然:要函数值较小,应该取在最外侧两零点之间,并且当时,到这最外侧两零点的距离之和为定值,即:.
那么,我们再考虑在之间的情况,同样可以得到相应的结果.以此类推,重复上述过程,
最终只剩下居中的零点,此时,只需要到的距离最小时,即:时,取最小值.
类似地,当偶数个绝对值相加时,重复上述过程(1)(2),最终将剩下居中的两个零点,此时,当任意,到这两零点的距离之和为定值,函数都可取到最小值.
建模:对于上述绝对值和函数,存在,使得对任意都有.且
(1)当为奇数时,;
(2)当为偶数时,.
模型检验:的选取与零点的个数n有关,与每个点之间的距离无关,特别的,当两点间的距离为0时,上述模型仍适用.
三、模型应用
问题(1)运用最值模型解答下列问题.
(i)函数的最小值.
解:,当时,.
讲解:模型的基本运用,本题是六个绝对值相加的情形.
(ii)不等式,对任意恒成立,其中,求实数的取值范围.
解:令,则.
当时,等号成立.
或
讲解:模型的转化运用,当不是整数时,也可以化归到整数的问题来解.
变式:思考若,是否还能使用最值模型求解?
当时,等号成立.
或
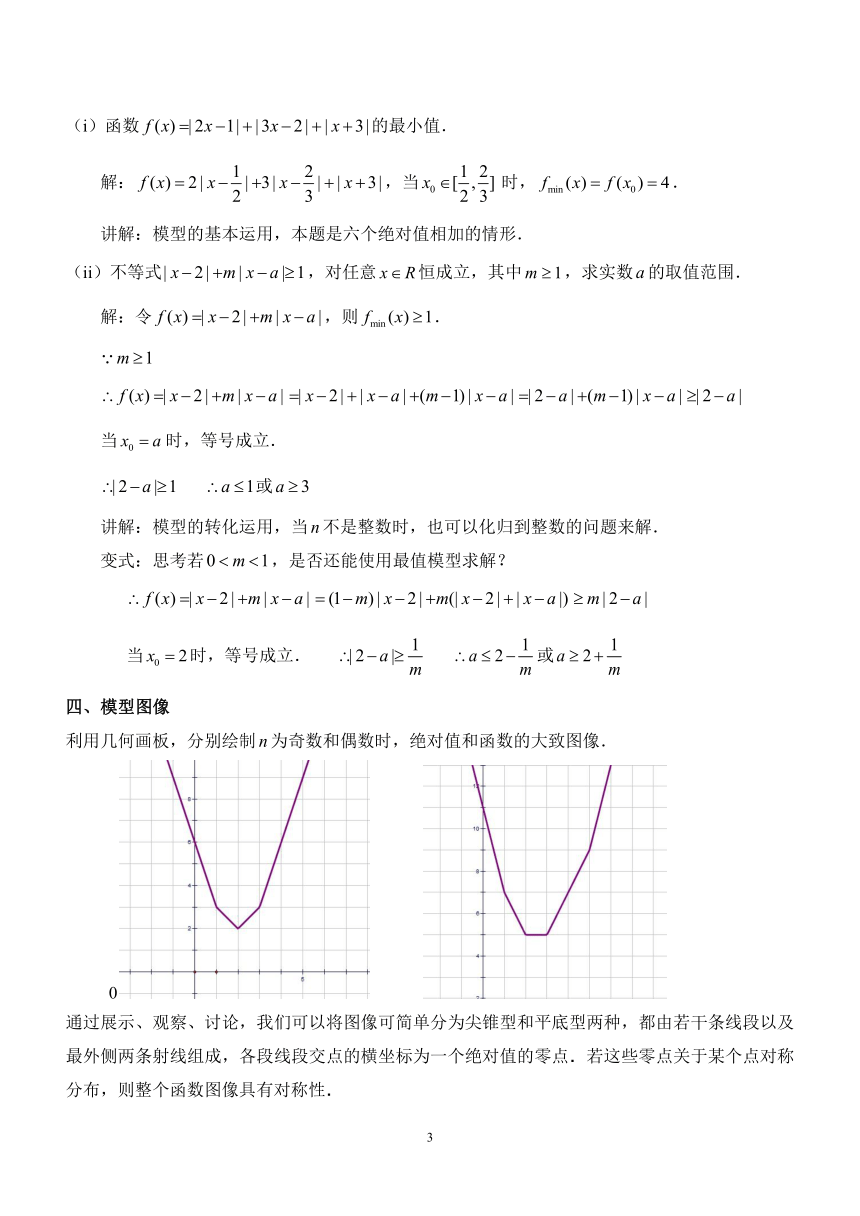
四、模型图像
利用几何画板,分别绘制为奇数和偶数时,绝对值和函数的大致图像.
0
通过展示、观察、讨论,我们可以将图像可简单分为尖锥型和平底型两种,都由若干条线段以及最外侧两条射线组成,各段线段交点的横坐标为一个绝对值的零点.若这些零点关于某个点对称分布,则整个函数图像具有对称性.
五、运用模型,体会感悟
问题(2)借助绝对值和函数的图像,并研究下列问题.
(i)(2012静安一模14)函数关于某条直线对称,求的值.
解:,,
讲解:简单高效,解决难题.
(ii)已知函数
且
,则满足条件的所有互异的整数的和是
.
解:(1)为偶函数,,解得或
(2)根据绝对值和函数性质,当也满足题意,解得
由(1)(2)得,所有互异的整数的和是4.
讲解:解答本题时,往往容易遗漏情况(2),此时需要我们对绝对值和函数的图像有直观的认识以及灵活的运用.
问题(3):(2009年上海市高考数学第14题)
如图:某地区的街道呈现网格状,相邻街距都为1,两街道相交点称为格点.若以互相垂直的两条街道为轴建立直角坐标系,现有格点(-2,2),(3,1),(3,4),(-2,3),(4,5),
(6,6)为报刊零售点.请确定一个格点(除零售点外)为发行站,使6个零售点沿街道到发行站之间路程之和最短.
解:为设发行站选址,到各零售点的距离之和可表示为:
根据绝对值和函数最值模型,当,时,取最小值,考虑到问题的实际情况,我们将发行站设置在点(3,3).
讲解:这道高考题,看似与我们今天的课题关系不大,但其实,通过化归,它实际上是将我们的模型推广到了二维的情况,在分别对进行最优化处理,问题得到了完美的解决.
六、课堂小结
平面几何里有一个基本公理:平面上两点之间的连线,线段最短.这里的最短,就是一种几何优化思想.今天我们通过绝对值和函数的几何意义,运用关于距离的基本公理,建立模型,并运用化归的思想,将许多复杂的问题加以转化,并最终用我们的模型轻松解决.今天的结论固然非常实用有效,我们探究问题的过程也一样精彩.
七、课后作业
(1)最后那道高考题,为我们打开了思路,使我们豁然开朗,在日常生活学习中,还有什么样的问题可以用今天的绝对值和函数模型来求解呢?请收集一些此类问题,或者进一步完善和拓展今天的绝对值和函数模型.
(2)根据本校教学大楼的紧急逃生路线图,根据所学的知识,建立数学模型.给出你认为最佳的逃生路线方案.(改编自2007年美国中学生数学建模竞赛
Problem
A).
教学设计说明:
本节课的特点
本节课是高一函数模型复习课,也是专题类的拓展与探究课.从绝对值的几何意义这个最简单的知识点开始,延伸开去,由点到线:将分奇偶数的整数个绝对值和函数最小值问题;非整数个绝对值和问题;绝对值和函数对称性问题以及二维环境下的绝对值和函数最优化问题这一系列问题加以串联.对近些年高考中能见到此类问题进行了一次全面的复习.同时,由线及面:将数学建模、化归、数形结合、分类讨论、概括归纳等重要数学融入到课堂教学的过程当中.
教学目标的设计
本节课课题的选取可谓非一日之功,而是源于我在近几年教学的点滴积累.特别是最近连续两年的高三教学经历,使我接触到大量的函数最值问题,在其中我对2009年上海高考的理科13题,(本课问题3)引发了我对绝对值和函数最值问题的思考.这看似简单的问题,其实有许多转化和应用,首先是系数为整数的绝对值和问题,再到系数为的问题,再到图像中的对称问题……,我意识到,探究这个问题的过程可以浓缩到一节课中,让学生也完整地经历一遍,一切就这样水到渠成了.
教学过程的设计
针对学生认知水平和实际情况,我设计了已解决问题为主线的教学过程.从作业中遇到的高考真题引入,突出绝对值几何意义解题的优点,激发学生深入探究的积极性.
建立模型,结论明确,便于记忆,并层层递进,逐个击破各类高考中出现过的问题.强调简单模型的广泛应用.
在整个教学过程中,遵循学生的思维过程,引导学生发现问题、解决问题,并在此过程体会化归的思想,主动参与问题的解决,在积累知识的同时,能力得到提高,提升思维品质.
反思与新认识
在教学实施过程中,基本达到了预设的教学目标,学生认知能力较强,使我们毫不费力就得到绝对值和函数的最值模型,并顺利的进入到模型运用于探究的环节.使得本节课整体比较紧凑,保证了教学目标的完成,课后,在与听课的专家老师交流和反思中发现,作为本节课的重点,模型建立的过程,还是有可以细细打磨的地方,比如建模实验过程,可以给学生更多参与的空间;再比如模型的严谨证明,也是研究数学问题的关键步骤.以后有机会,或者在较低年级开设拓展课程是,可以进一步完善.
1
教学目标
理解绝对值和函数的几何意义,归纳概括绝对值和函数最值的数学模型.
利用绝对值和函数最值的数学模型,运用化归的思想方法,解决相关问题.
通过创设情境,初步形成自主研究数学问题的能力,养成层层递进地思考数学问题的习惯,体验突破困难取得成功的喜悦.
教学重点:
绝对值和函数性质的探究与其最值数学模型的建模过程.
教学难点:
运用绝对值和函数最值的数学模型解决相关问题.
教学过程:
一、引入课题
我们在作业中遇到过这样一道高考题:
引例(1)(2014安徽)若函数的最小值为,则的值_______.
(解法一)分类讨论、零点分段
当a≥2时,f(x)=
当a<2时,f(x)=
综上可知,a的值为-4或8.
(解法二)几何意义:距离之和
根据绝对值的几何意义,此函数可看做是数轴上一点到的距离与到距离的两倍之和,显然,当介于与之间时,为定值,只需使剩下的取到最小值0时,函数值最小.因此
.a的值为-4或8.
解法一是绝对值和函数问题的常规解法,不过解法二更加高效简洁,形象生动.将上述例题看作是3个绝对值相加的问题,那么如果改变题中绝对值的个数,如4个、5个……绝对值相加,问题的情形会发生哪些变化,它们的一般情况是什么样的呢?今天我们就这个问题做一个深入的探究.
二、模型建立
我们把形如,其中,
的函数称作绝对值和函数.根据绝对值的几何意义,在其定义域上没有最大值,而有最小值,并且最小值处的自变量取值与函数中绝对值的零点有关.
问题分析:类似于例题的情况,当奇数个绝对值相加时,函数的几何意义为数轴上的一点到个零点的距离之和.
显然:要函数值较小,应该取在最外侧两零点之间,并且当时,到这最外侧两零点的距离之和为定值,即:.
那么,我们再考虑在之间的情况,同样可以得到相应的结果.以此类推,重复上述过程,
最终只剩下居中的零点,此时,只需要到的距离最小时,即:时,取最小值.
类似地,当偶数个绝对值相加时,重复上述过程(1)(2),最终将剩下居中的两个零点,此时,当任意,到这两零点的距离之和为定值,函数都可取到最小值.
建模:对于上述绝对值和函数,存在,使得对任意都有.且
(1)当为奇数时,;
(2)当为偶数时,.
模型检验:的选取与零点的个数n有关,与每个点之间的距离无关,特别的,当两点间的距离为0时,上述模型仍适用.
三、模型应用
问题(1)运用最值模型解答下列问题.
(i)函数的最小值.
解:,当时,.
讲解:模型的基本运用,本题是六个绝对值相加的情形.
(ii)不等式,对任意恒成立,其中,求实数的取值范围.
解:令,则.
当时,等号成立.
或
讲解:模型的转化运用,当不是整数时,也可以化归到整数的问题来解.
变式:思考若,是否还能使用最值模型求解?
当时,等号成立.
或
四、模型图像
利用几何画板,分别绘制为奇数和偶数时,绝对值和函数的大致图像.
0
通过展示、观察、讨论,我们可以将图像可简单分为尖锥型和平底型两种,都由若干条线段以及最外侧两条射线组成,各段线段交点的横坐标为一个绝对值的零点.若这些零点关于某个点对称分布,则整个函数图像具有对称性.
五、运用模型,体会感悟
问题(2)借助绝对值和函数的图像,并研究下列问题.
(i)(2012静安一模14)函数关于某条直线对称,求的值.
解:,,
讲解:简单高效,解决难题.
(ii)已知函数
且
,则满足条件的所有互异的整数的和是
.
解:(1)为偶函数,,解得或
(2)根据绝对值和函数性质,当也满足题意,解得
由(1)(2)得,所有互异的整数的和是4.
讲解:解答本题时,往往容易遗漏情况(2),此时需要我们对绝对值和函数的图像有直观的认识以及灵活的运用.
问题(3):(2009年上海市高考数学第14题)
如图:某地区的街道呈现网格状,相邻街距都为1,两街道相交点称为格点.若以互相垂直的两条街道为轴建立直角坐标系,现有格点(-2,2),(3,1),(3,4),(-2,3),(4,5),
(6,6)为报刊零售点.请确定一个格点(除零售点外)为发行站,使6个零售点沿街道到发行站之间路程之和最短.
解:为设发行站选址,到各零售点的距离之和可表示为:
根据绝对值和函数最值模型,当,时,取最小值,考虑到问题的实际情况,我们将发行站设置在点(3,3).
讲解:这道高考题,看似与我们今天的课题关系不大,但其实,通过化归,它实际上是将我们的模型推广到了二维的情况,在分别对进行最优化处理,问题得到了完美的解决.
六、课堂小结
平面几何里有一个基本公理:平面上两点之间的连线,线段最短.这里的最短,就是一种几何优化思想.今天我们通过绝对值和函数的几何意义,运用关于距离的基本公理,建立模型,并运用化归的思想,将许多复杂的问题加以转化,并最终用我们的模型轻松解决.今天的结论固然非常实用有效,我们探究问题的过程也一样精彩.
七、课后作业
(1)最后那道高考题,为我们打开了思路,使我们豁然开朗,在日常生活学习中,还有什么样的问题可以用今天的绝对值和函数模型来求解呢?请收集一些此类问题,或者进一步完善和拓展今天的绝对值和函数模型.
(2)根据本校教学大楼的紧急逃生路线图,根据所学的知识,建立数学模型.给出你认为最佳的逃生路线方案.(改编自2007年美国中学生数学建模竞赛
Problem
A).
教学设计说明:
本节课的特点
本节课是高一函数模型复习课,也是专题类的拓展与探究课.从绝对值的几何意义这个最简单的知识点开始,延伸开去,由点到线:将分奇偶数的整数个绝对值和函数最小值问题;非整数个绝对值和问题;绝对值和函数对称性问题以及二维环境下的绝对值和函数最优化问题这一系列问题加以串联.对近些年高考中能见到此类问题进行了一次全面的复习.同时,由线及面:将数学建模、化归、数形结合、分类讨论、概括归纳等重要数学融入到课堂教学的过程当中.
教学目标的设计
本节课课题的选取可谓非一日之功,而是源于我在近几年教学的点滴积累.特别是最近连续两年的高三教学经历,使我接触到大量的函数最值问题,在其中我对2009年上海高考的理科13题,(本课问题3)引发了我对绝对值和函数最值问题的思考.这看似简单的问题,其实有许多转化和应用,首先是系数为整数的绝对值和问题,再到系数为的问题,再到图像中的对称问题……,我意识到,探究这个问题的过程可以浓缩到一节课中,让学生也完整地经历一遍,一切就这样水到渠成了.
教学过程的设计
针对学生认知水平和实际情况,我设计了已解决问题为主线的教学过程.从作业中遇到的高考真题引入,突出绝对值几何意义解题的优点,激发学生深入探究的积极性.
建立模型,结论明确,便于记忆,并层层递进,逐个击破各类高考中出现过的问题.强调简单模型的广泛应用.
在整个教学过程中,遵循学生的思维过程,引导学生发现问题、解决问题,并在此过程体会化归的思想,主动参与问题的解决,在积累知识的同时,能力得到提高,提升思维品质.
反思与新认识
在教学实施过程中,基本达到了预设的教学目标,学生认知能力较强,使我们毫不费力就得到绝对值和函数的最值模型,并顺利的进入到模型运用于探究的环节.使得本节课整体比较紧凑,保证了教学目标的完成,课后,在与听课的专家老师交流和反思中发现,作为本节课的重点,模型建立的过程,还是有可以细细打磨的地方,比如建模实验过程,可以给学生更多参与的空间;再比如模型的严谨证明,也是研究数学问题的关键步骤.以后有机会,或者在较低年级开设拓展课程是,可以进一步完善.
1
