湖南省张家界市永定区2020-2021学年八年级下学期期末考试数学试题(Word版 含答案)
文档属性
| 名称 | 湖南省张家界市永定区2020-2021学年八年级下学期期末考试数学试题(Word版 含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 793.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-07 09:31:01 | ||
图片预览


文档简介
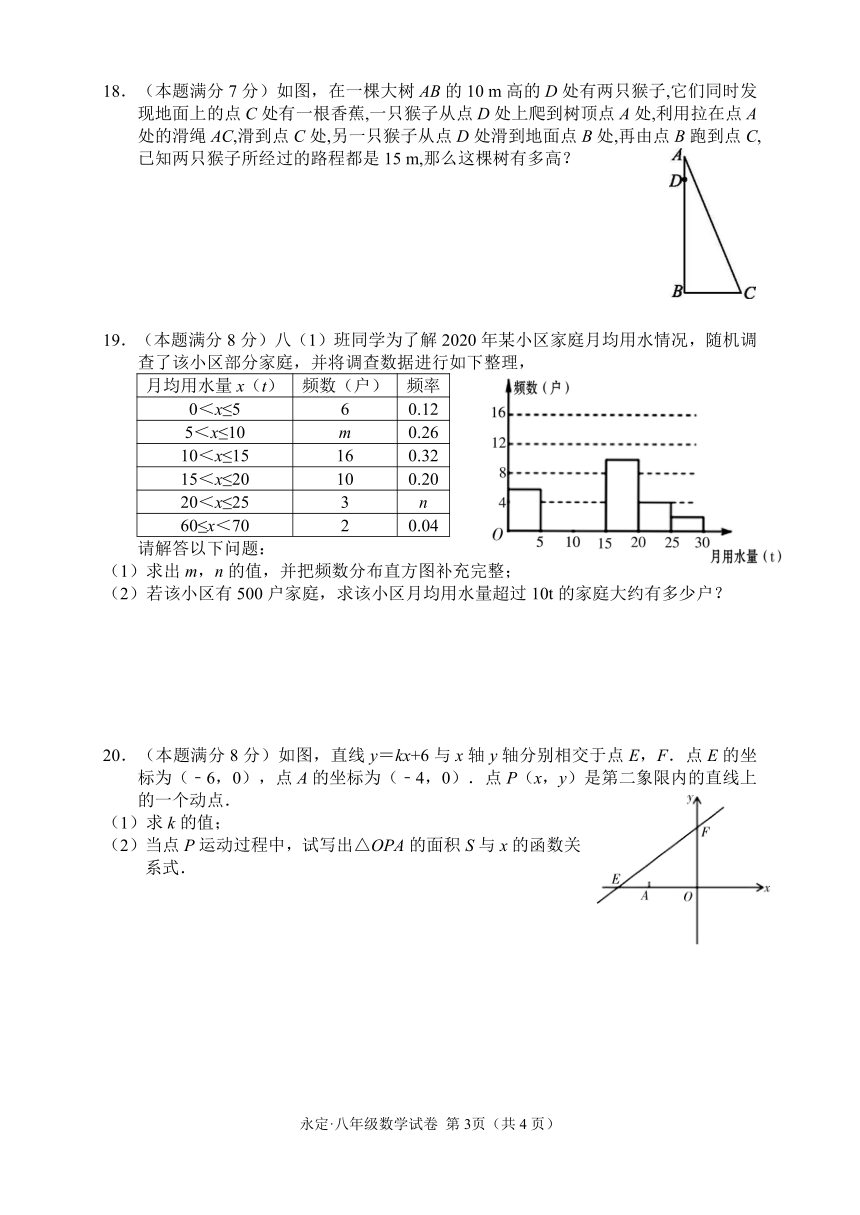
永定区2021年春季八年级期末质量检测试卷
数
学
题
号
一
二
三
总
分
得
分
考生注意:本卷共三道题,满分100分,时量120分钟。
一、选择题(本大题共8个小题,每小题3分,满分24分.请将正确答案的字母代号填在下表中)
题号
1
2
3
4
5
6
7
8
答案
1.下列图形中,是中心对称图形的是
A.
B.
C.
D.
2.下列所给出的点中,在第三象限的是
A.(3,2)
B.(﹣3,﹣2)
C.(3,﹣2)
D.(﹣3,2)
3.下列各组数中,不能作为直角三角形的三边长的是
A.5,4,3
B.5,12,13
C.6,8,10
D.6,4,7
4.将50个数据分成5组列出频数分布表,其中第一组的频数为5,第二组与第五组的频数和为20,第三组的频率为0.2,则第四组的频率为
A.0.3
B.0.5
C.12
D.25
5.如图,菱形ABCD中,对角线AC与BD相交于点O,H为AD边的中点,BC=8cm,则OH的长为
A.8cm
B.6cm
C.4cm
D.2cm
6.对于函数y=-2x+1,下列结论正确的是
A.y值随x值的增大而增大
B.它的图象与x轴交点坐标为(,0)
C.它的图象必经过点(1,-3)
D.它的图象经过第一、二、三象限
7.在矩形ABCD中,AB=6,将△ABD沿对角线BD对折,得到△EBD,DE与
BC交于点F,∠ADB=30°,则EF的长为
A.
B.2
C.3
D.3
8.定义:,,,,,,例如:,,,,,,则g(f(5,-2))=
A.(2,
-5)
B.(-2,5)
C.(-5,2)
D.(-2,-5)
二、填空题(本大题共6个小题,
每小题3分,
满分18分)
9.点(-1,3)关于轴对称的点坐标是
.
10.若一个多边形的每个外角都等于45°,则这个多边形的边数是
.
11.一个水库的水位在最近5h内持续上涨.下表记录了这5h内6个时间点的水位高度,其中x表示时间,y表示水位高度.
x/h
0
1
2
3
4
5
y/m
3
3.2
3.4
3.6
3.8
4
根据表格中水位的变化规律,则y与x的函数表达式为
.
12.若正比例函数中,y随x的增大而增大,则m的值为
.
13.如图,直线EF经过平行四边形ABCD的对角线的交点O,若四边形AEFB的面积为20cm2,则平行四边形ABCD的面积为
cm2.
14.如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交AC,AB于点M、N,再分别以点M、N为圆心,大于MN的长为半径画弧,两弧交于点P,作射线AP交边BC于点D,若CD=2,AB=8,则△ABD的面积是
.
三、解答题(本大题共8个小题,满分58分)
15.(本题满分5分)已知一次函数图象经过(0,-1)和(2,3)两点.
(1)求此一次函数的解析式;
(2)若点(m,-3)在函数图象上,求m的值.
16.(本题满分5分)已知:如图,在四边形ABCD中,AC与BD相交于点O,AB∥CD,
BO=DO.
求证:四边形ABCD是平行四边形.
17.(本题满分7分)如图,AD是△ABC的中线,DE⊥AB于点E,DF⊥AC于点F,且BE=CF.
求证:(1)AD是∠BAC的平分线;(2)AB=AC.
18.(本题满分7分)如图,在一棵大树AB的10
m高的D处有两只猴子,它们同时发现地面上的点C处有一根香蕉,一只猴子从点D处上爬到树顶点A处,利用拉在点A处的滑绳AC,滑到点C处,另一只猴子从点D处滑到地面点B处,再由点B跑到点C,已知两只猴子所经过的路程都是15
m,那么这棵树有多高?
19.(本题满分8分)八(1)班同学为了解2020年某小区家庭月均用水情况,随机调查了该小区部分家庭,并将调查数据进行如下整理,
月均用水量x(t)
频数(户)
频率
0<x≤5
6
0.12
5<x≤10
m
0.26
10<x≤15
16
0.32
15<x≤20
10
0.20
20<x≤25
3
n
60≤x<70
2
0.04
请解答以下问题:
(1)求出m,n的值,并把频数分布直方图补充完整;
(2)若该小区有500户家庭,求该小区月均用水量超过10t的家庭大约有多少户?
20.(本题满分8分)如图,直线y=kx+6与x轴y轴分别相交于点E,F.点E的坐标为(﹣6,0),点A的坐标为(﹣4,0).点P(x,y)是第二象限内的直线上的一个动点.
(1)求k的值;
(2)当点P运动过程中,试写出△OPA的面积S与x的函数关系式.
21.(本题满分8分)周末,小华和爸爸骑自行车从家出发去森林公园游玩,当他骑了一段路时,想起要在新华书店买一本书,于是原路返回到刚经过的新华书店,买到书后继续前往森林公园,如图是他离家的距离与时间的关系示意图,请根据图中提供的信息回答下列问题:
(1)小华家离森林公园的距离是
米;
(2)小华在新华书店停留了
分钟;
(3)买到书后,小华从新华书店到森林公园骑车的平均速度是
米/分;
(4)本次去森林公园途中,小华一共行驶了
米.
22.(本题满分10分)将两块完全相同的且含60°角的直角三角板ABC与AFE按①所示的方式放置.现将Rt△AEF绕点A按逆时针方向旋转∠α(0°<α<90°),如图图②,AE与BC交于点M,AC与EF交于点N,BC与EF交于点P.
(1)求证:AM=AN
;
(2)当旋转角∠α等于多少度时,四边形ABPF是菱形?说明理由.
永定区2021春季八年级期末质量检测试卷
数学参考答案
一、选择题(本大题共8个小题,
每小题3分,满分24分)
题号
1
2
3
4
5
6
7
8
答案
C
B
D
A
C
B
B
A
二、填空题(本大题共6个小题,
每小题3分,
满分18分)
9.(-1,-3)
10.8
11.y=0.2x+3
12.2
13.40
14.8
三、解答题(本大题共9个小题,满分58分)
15.(1)y=2x-1,
(3分)
(2)-1(2分)
16.略
17.证明:(1)∵DE⊥AB,DF⊥AC,∴∠BED=∠CFD=90°.
又∵BD=CD,BE=CF,∴Rt△BDE≌Rt△CDF,
∴DE=DF.又∵DE⊥AB,DF⊥AC,
∴AD是∠BAC的平分线.……………………5分
(2)由(1)知△BDE≌△CDF,∴∠B=∠C,∴AB=AC.
……………………7分
18.解:设树高AB为x
m.
由题意知BC=15-10=5(m),AD=(x-10)m,AC=15-AD=15-x+10=(25-x)m.
在
Rt△ABC中,AB2+BC2=AC2,
即x2+52=(25-x)2,解得x=12.答:这棵树有12
m高。
19.解:(1)13,
0.06,图略;(6分)
(2)500×(0.32+0.2+0.06+0.04)=310(户),
答:该小区月均用水量超过10t的家庭大约有310户.(2分)
20.解:(1)把E(﹣6,0)代入直线解析式得:0=﹣6k+6,
解得:k=1;……………………3分
(2)根据题意得:S=OA?|yP纵坐标|=×4×y=2y,
把P(x,y)代入解析式得:y=x+6,
则S=2x+12.
……………………8分
21.解:(1)3400;(2)8;(3)350;(4)5000
22.(1)证明:∵∠α+∠EAC=90°,∠NAF+∠EAC=90°,
∴∠α=∠NAF.
又∵∠B=∠F,AB=AF,
∴△ABM≌△AFN,∴AM=AN.
……………………5分
(2)当旋转角∠α=30°时,四边形ABPF是菱形.理由:
……………………6分
∵∠α=30°,∠EAF=90°,
∴∠BAF=120°.
又∵∠B=∠F=60°,
∴∠B+∠BAF=60°+120°=180°,∠F+∠BAF=60°+120°=180°,
∴AF∥BP,AB∥PF,
∴四边形ABPF是平行四边形.
又∵△ABM≌△AFN,∴AB=AF,
∴四边形ABPF是菱形.
……………………10分
O
永定·八年级数学试卷
第1页(共4页)
数
学
题
号
一
二
三
总
分
得
分
考生注意:本卷共三道题,满分100分,时量120分钟。
一、选择题(本大题共8个小题,每小题3分,满分24分.请将正确答案的字母代号填在下表中)
题号
1
2
3
4
5
6
7
8
答案
1.下列图形中,是中心对称图形的是
A.
B.
C.
D.
2.下列所给出的点中,在第三象限的是
A.(3,2)
B.(﹣3,﹣2)
C.(3,﹣2)
D.(﹣3,2)
3.下列各组数中,不能作为直角三角形的三边长的是
A.5,4,3
B.5,12,13
C.6,8,10
D.6,4,7
4.将50个数据分成5组列出频数分布表,其中第一组的频数为5,第二组与第五组的频数和为20,第三组的频率为0.2,则第四组的频率为
A.0.3
B.0.5
C.12
D.25
5.如图,菱形ABCD中,对角线AC与BD相交于点O,H为AD边的中点,BC=8cm,则OH的长为
A.8cm
B.6cm
C.4cm
D.2cm
6.对于函数y=-2x+1,下列结论正确的是
A.y值随x值的增大而增大
B.它的图象与x轴交点坐标为(,0)
C.它的图象必经过点(1,-3)
D.它的图象经过第一、二、三象限
7.在矩形ABCD中,AB=6,将△ABD沿对角线BD对折,得到△EBD,DE与
BC交于点F,∠ADB=30°,则EF的长为
A.
B.2
C.3
D.3
8.定义:,,,,,,例如:,,,,,,则g(f(5,-2))=
A.(2,
-5)
B.(-2,5)
C.(-5,2)
D.(-2,-5)
二、填空题(本大题共6个小题,
每小题3分,
满分18分)
9.点(-1,3)关于轴对称的点坐标是
.
10.若一个多边形的每个外角都等于45°,则这个多边形的边数是
.
11.一个水库的水位在最近5h内持续上涨.下表记录了这5h内6个时间点的水位高度,其中x表示时间,y表示水位高度.
x/h
0
1
2
3
4
5
y/m
3
3.2
3.4
3.6
3.8
4
根据表格中水位的变化规律,则y与x的函数表达式为
.
12.若正比例函数中,y随x的增大而增大,则m的值为
.
13.如图,直线EF经过平行四边形ABCD的对角线的交点O,若四边形AEFB的面积为20cm2,则平行四边形ABCD的面积为
cm2.
14.如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交AC,AB于点M、N,再分别以点M、N为圆心,大于MN的长为半径画弧,两弧交于点P,作射线AP交边BC于点D,若CD=2,AB=8,则△ABD的面积是
.
三、解答题(本大题共8个小题,满分58分)
15.(本题满分5分)已知一次函数图象经过(0,-1)和(2,3)两点.
(1)求此一次函数的解析式;
(2)若点(m,-3)在函数图象上,求m的值.
16.(本题满分5分)已知:如图,在四边形ABCD中,AC与BD相交于点O,AB∥CD,
BO=DO.
求证:四边形ABCD是平行四边形.
17.(本题满分7分)如图,AD是△ABC的中线,DE⊥AB于点E,DF⊥AC于点F,且BE=CF.
求证:(1)AD是∠BAC的平分线;(2)AB=AC.
18.(本题满分7分)如图,在一棵大树AB的10
m高的D处有两只猴子,它们同时发现地面上的点C处有一根香蕉,一只猴子从点D处上爬到树顶点A处,利用拉在点A处的滑绳AC,滑到点C处,另一只猴子从点D处滑到地面点B处,再由点B跑到点C,已知两只猴子所经过的路程都是15
m,那么这棵树有多高?
19.(本题满分8分)八(1)班同学为了解2020年某小区家庭月均用水情况,随机调查了该小区部分家庭,并将调查数据进行如下整理,
月均用水量x(t)
频数(户)
频率
0<x≤5
6
0.12
5<x≤10
m
0.26
10<x≤15
16
0.32
15<x≤20
10
0.20
20<x≤25
3
n
60≤x<70
2
0.04
请解答以下问题:
(1)求出m,n的值,并把频数分布直方图补充完整;
(2)若该小区有500户家庭,求该小区月均用水量超过10t的家庭大约有多少户?
20.(本题满分8分)如图,直线y=kx+6与x轴y轴分别相交于点E,F.点E的坐标为(﹣6,0),点A的坐标为(﹣4,0).点P(x,y)是第二象限内的直线上的一个动点.
(1)求k的值;
(2)当点P运动过程中,试写出△OPA的面积S与x的函数关系式.
21.(本题满分8分)周末,小华和爸爸骑自行车从家出发去森林公园游玩,当他骑了一段路时,想起要在新华书店买一本书,于是原路返回到刚经过的新华书店,买到书后继续前往森林公园,如图是他离家的距离与时间的关系示意图,请根据图中提供的信息回答下列问题:
(1)小华家离森林公园的距离是
米;
(2)小华在新华书店停留了
分钟;
(3)买到书后,小华从新华书店到森林公园骑车的平均速度是
米/分;
(4)本次去森林公园途中,小华一共行驶了
米.
22.(本题满分10分)将两块完全相同的且含60°角的直角三角板ABC与AFE按①所示的方式放置.现将Rt△AEF绕点A按逆时针方向旋转∠α(0°<α<90°),如图图②,AE与BC交于点M,AC与EF交于点N,BC与EF交于点P.
(1)求证:AM=AN
;
(2)当旋转角∠α等于多少度时,四边形ABPF是菱形?说明理由.
永定区2021春季八年级期末质量检测试卷
数学参考答案
一、选择题(本大题共8个小题,
每小题3分,满分24分)
题号
1
2
3
4
5
6
7
8
答案
C
B
D
A
C
B
B
A
二、填空题(本大题共6个小题,
每小题3分,
满分18分)
9.(-1,-3)
10.8
11.y=0.2x+3
12.2
13.40
14.8
三、解答题(本大题共9个小题,满分58分)
15.(1)y=2x-1,
(3分)
(2)-1(2分)
16.略
17.证明:(1)∵DE⊥AB,DF⊥AC,∴∠BED=∠CFD=90°.
又∵BD=CD,BE=CF,∴Rt△BDE≌Rt△CDF,
∴DE=DF.又∵DE⊥AB,DF⊥AC,
∴AD是∠BAC的平分线.……………………5分
(2)由(1)知△BDE≌△CDF,∴∠B=∠C,∴AB=AC.
……………………7分
18.解:设树高AB为x
m.
由题意知BC=15-10=5(m),AD=(x-10)m,AC=15-AD=15-x+10=(25-x)m.
在
Rt△ABC中,AB2+BC2=AC2,
即x2+52=(25-x)2,解得x=12.答:这棵树有12
m高。
19.解:(1)13,
0.06,图略;(6分)
(2)500×(0.32+0.2+0.06+0.04)=310(户),
答:该小区月均用水量超过10t的家庭大约有310户.(2分)
20.解:(1)把E(﹣6,0)代入直线解析式得:0=﹣6k+6,
解得:k=1;……………………3分
(2)根据题意得:S=OA?|yP纵坐标|=×4×y=2y,
把P(x,y)代入解析式得:y=x+6,
则S=2x+12.
……………………8分
21.解:(1)3400;(2)8;(3)350;(4)5000
22.(1)证明:∵∠α+∠EAC=90°,∠NAF+∠EAC=90°,
∴∠α=∠NAF.
又∵∠B=∠F,AB=AF,
∴△ABM≌△AFN,∴AM=AN.
……………………5分
(2)当旋转角∠α=30°时,四边形ABPF是菱形.理由:
……………………6分
∵∠α=30°,∠EAF=90°,
∴∠BAF=120°.
又∵∠B=∠F=60°,
∴∠B+∠BAF=60°+120°=180°,∠F+∠BAF=60°+120°=180°,
∴AF∥BP,AB∥PF,
∴四边形ABPF是平行四边形.
又∵△ABM≌△AFN,∴AB=AF,
∴四边形ABPF是菱形.
……………………10分
O
永定·八年级数学试卷
第1页(共4页)
同课章节目录
