湖南省怀化市会同县2019-2020学年八年级下学期期末考试数学试题(Word版 含答案)
文档属性
| 名称 | 湖南省怀化市会同县2019-2020学年八年级下学期期末考试数学试题(Word版 含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 1005.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-07 09:38:17 | ||
图片预览


文档简介
2020年上期八年级期末质量监测卷
数
学
说明:
1.本试卷分试题卷和答题卡两部分。此系试题卷。满分150分,时量120分钟。
2.所有答案都必须做在答题卡标定的位置上,务必注意试题序号和答题卡序号相对应。
一、选择题(每小题4分,共40分)
1.
既是中心对称又是轴对称的图形是
A.等边三角形
B.平等四边形
C.圆
D.等腰梯形
2.
等边三角形的边长为12,则它的中位线长是
A.5
B.6
C.7
D.8
3.
如图为一次函数的图象,则下式一定正确的是
A.
B.
C.
D.
4.
函数中自变量的取值范围是
A.
B.
C.
D.且
5.
六边形的内角和是(
)°
A.540°
B.720°
C.900°
D.1080°
6.
已知如图:菱形ABCD中,边长为8,∠A=60°,则DB=(
)
A.4
B.
C.
D.8
7.
如图所示:在Rt△ABC中,∠A=30°,DE是斜边AC的中垂线分别交AB、AC于D、E两点,BD=1,则AC=
A.
B.
C.
D.
8.
已知如图,∠B=∠D=90°,BC=CD,∠1=30°,则∠2=
A.60°
B.50°
C.40°
D.30°
9.
在平面直角坐标系中,一个智能机器人接到如下指令:从原点O出发,按向右、向上、向右、向下的方向依次不断移动,每次移动1m,其行走路线如图所示,第1次移动到A1,第2次移动到A2……第n次移动到An,则△OA2A2020的面积是
A.505m2
B.m2
C.m2
D.1008
m2
10.
如图,在△ABC点D为AC的中点,且DB⊥BC,BC=4,CD=5,则△ABC中,BC边上的高为
A.6
B.7
C.8
D.9
二、填空题(每小题4分,共24分)
11.
在平面直角坐标系的第二象限内有一点M,点M到轴的距离为3,到轴的距离为4,则点M的坐标是
.
12.
一个多边形的内角和是外角和的3倍,则这个多边形的边数
边.
13.
我们学校在一次竞赛中有40名同学进入复赛,我们把成绩分为六组,第一组至第四组的人数分别为10、5、7、6,第五组的频率是0.2,则第六组的频率是:
.
14.
已知如图:A、B坐标分别为A(1,0),B(0,2),将线段AB平移到.它的坐标分别为A1(2,),B1(,3),则
.
15.
已知如图:在菱形ABCD中,对角线AC、BD相交于点O,请添加一条件,使菱形为正方形,这个条件是
.
16.
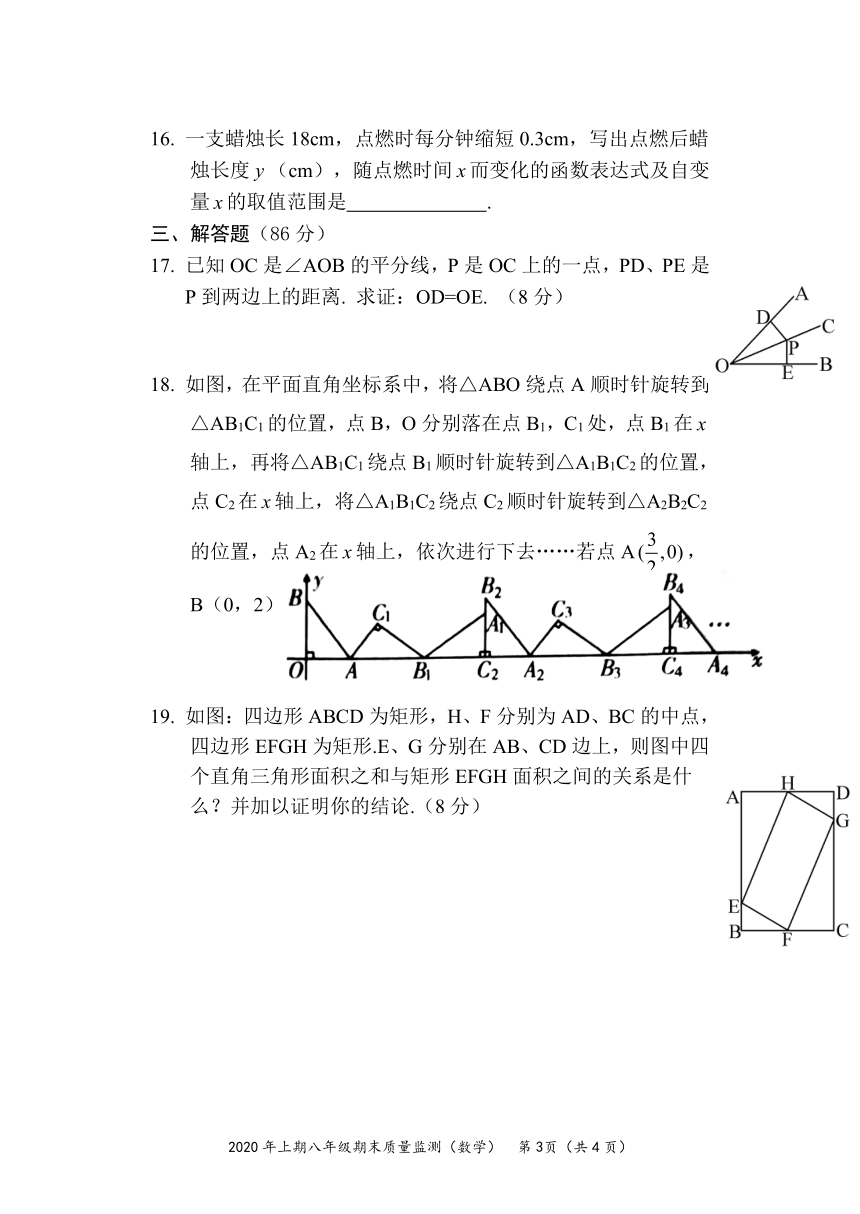
一支蜡烛长18cm,点燃时每分钟缩短0.3cm,写出点燃后蜡烛长度(cm),随点燃时间而变化的函数表达式及自变量的取值范围是
.
三、解答题(86分)
17.
已知OC是∠AOB的平分线,P是OC上的一点,PD、PE是P到两边上的距离.
求证:OD=OE.
(8分)
18.
如图,在平面直角坐标系中,将△ABO绕点A顺时针旋转到△AB1C1的位置,点B,O分别落在点B1,C1处,点B1在轴上,再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置,点C2在轴上,将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置,点A2在轴上,依次进行下去……若点A,B(0,2),则点B2020的坐标是什么?
19.
如图:四边形ABCD为矩形,H、F分别为AD、BC的中点,四边形EFGH为矩形.E、G分别在AB、CD边上,则图中四个直角三角形面积之和与矩形EFGH面积之间的关系是什么?并加以证明你的结论.(8分)
20.
我们学校举行歌咏比赛,组委规定任何一名参赛选手成绩满足赛后整理所有参赛选手的成绩如右表:(6分)
请求出、.
21.
已知如图:矩形ABCD中,AB=4,BC=2.点E、F分别在AB、CD上,且BE=DF=.(8分)
(1)证明:四边形AECF是菱形.
(2)求EF的长度.
22.
如图直线∶和相交于点P(,),与轴交于点A.
与轴交于点B.(8分)
(1)求直线的表达式.
(2)求△ABP的面积.
23.
如图,矩形ABCD中,AB=8,AD=6。点O是对角线BD的中点,过点O的直线分别交AB、CD边于点E、F.(10分)
(1)求证:四边形DEBF是平行四边形.
(2)当DE=DF时,求EF.
24.
如图:△ABC是边长为3cm的等边三角形动点P、Q同时从A、B两点出发,分别沿AB、BC方向匀速移动,它们的速度都是1cm/s,当点P到达B时,P、Q两点停止运动,设点P到达B时,P、Q两点停止运动.设点P运动的时间为t(s).当t为何值时,△PBQ是直角三角形?(10分)
25.
学校为了美化环境,计划分两次购进A、B两种花.(两次价格相同)(12分)
(1)求A、B两种花的单价?
(2)若购买A、B两种花共31棵,且B种
花的数量不大于A种花的数量的2倍.
请给出一种费用最省的方案,并求出该方案所需费用.
26.
将一个直角三角形纸片ABO放置在平面直角坐标系中,点A(,0),点B(0,1),P是边AB上的一点(点P不与A、B重合)沿着P折叠该纸片得点的对应点A′.
(1)如图①当点A′在第一象限,且满足A′B⊥OB时,求A′的坐标.
(2)如图②当P为AB的中点时,求A′B的长.
2020年上期八年级期末质量监测卷
数学参考答案
一、选择题:1——10:C
B
D
D
B
D
B
A
A
A
二、填空:11.(-4,3)
12.
8
13.
0.1
14.
2
15.略(符合题意即可)
16.
三、17.
利用H、L定理证得
18.
利用勾股定理计算:B2(6,2)
B4(12,2)……B2020(6×1010,2)即B2020(6060,2)
19.
相等,提示,连HF利用等底同高,面积相等或其它方法可。
20.
21.
(1)计算后,知AECF为菱形
(2)连AC,则AC=2,∴
22.(1)
(2)与轴交点C(-1,0)
23.
(1)结论成立
(2)DO==5,∵DE=DF,四边形DEBF是菱形,设AE=,则DE=,
∴,∴
24.
(1)
∵,另一情况:
∴当或2时,△PBQ是Rt△.
25.
(1)设A、B两花单价为、,则
(2)要费用最省,需最小且、自然数,∴时,符合题意,费用11×20+20×5=320元
26.
(1)∵A()B(0,1)由对叠可知OA′=OA=,∴A′B=
∴A′(,1)
(2)∵P是中点,AB=,∴OP=为等边三角形,又根据对叠的性质,A′P=AP=1=OB,∠BOA′=60°-∠A′OP=60°-∠POA=30°=∠OAP=∠OA′P=30°A′P∥OB四边形OPA′B是□,∴A′B=OP=1.
(在Rt△AOB中,∠OAB=30°)
分数段
频数
频率
30
0.15
0.45
60
20
0.1
A
B
开支
一次
30
15
675
二次
12
5
265
PAGE
2020年上期八年级期末质量监测(数学)
第1页(共4页)
数
学
说明:
1.本试卷分试题卷和答题卡两部分。此系试题卷。满分150分,时量120分钟。
2.所有答案都必须做在答题卡标定的位置上,务必注意试题序号和答题卡序号相对应。
一、选择题(每小题4分,共40分)
1.
既是中心对称又是轴对称的图形是
A.等边三角形
B.平等四边形
C.圆
D.等腰梯形
2.
等边三角形的边长为12,则它的中位线长是
A.5
B.6
C.7
D.8
3.
如图为一次函数的图象,则下式一定正确的是
A.
B.
C.
D.
4.
函数中自变量的取值范围是
A.
B.
C.
D.且
5.
六边形的内角和是(
)°
A.540°
B.720°
C.900°
D.1080°
6.
已知如图:菱形ABCD中,边长为8,∠A=60°,则DB=(
)
A.4
B.
C.
D.8
7.
如图所示:在Rt△ABC中,∠A=30°,DE是斜边AC的中垂线分别交AB、AC于D、E两点,BD=1,则AC=
A.
B.
C.
D.
8.
已知如图,∠B=∠D=90°,BC=CD,∠1=30°,则∠2=
A.60°
B.50°
C.40°
D.30°
9.
在平面直角坐标系中,一个智能机器人接到如下指令:从原点O出发,按向右、向上、向右、向下的方向依次不断移动,每次移动1m,其行走路线如图所示,第1次移动到A1,第2次移动到A2……第n次移动到An,则△OA2A2020的面积是
A.505m2
B.m2
C.m2
D.1008
m2
10.
如图,在△ABC点D为AC的中点,且DB⊥BC,BC=4,CD=5,则△ABC中,BC边上的高为
A.6
B.7
C.8
D.9
二、填空题(每小题4分,共24分)
11.
在平面直角坐标系的第二象限内有一点M,点M到轴的距离为3,到轴的距离为4,则点M的坐标是
.
12.
一个多边形的内角和是外角和的3倍,则这个多边形的边数
边.
13.
我们学校在一次竞赛中有40名同学进入复赛,我们把成绩分为六组,第一组至第四组的人数分别为10、5、7、6,第五组的频率是0.2,则第六组的频率是:
.
14.
已知如图:A、B坐标分别为A(1,0),B(0,2),将线段AB平移到.它的坐标分别为A1(2,),B1(,3),则
.
15.
已知如图:在菱形ABCD中,对角线AC、BD相交于点O,请添加一条件,使菱形为正方形,这个条件是
.
16.
一支蜡烛长18cm,点燃时每分钟缩短0.3cm,写出点燃后蜡烛长度(cm),随点燃时间而变化的函数表达式及自变量的取值范围是
.
三、解答题(86分)
17.
已知OC是∠AOB的平分线,P是OC上的一点,PD、PE是P到两边上的距离.
求证:OD=OE.
(8分)
18.
如图,在平面直角坐标系中,将△ABO绕点A顺时针旋转到△AB1C1的位置,点B,O分别落在点B1,C1处,点B1在轴上,再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置,点C2在轴上,将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置,点A2在轴上,依次进行下去……若点A,B(0,2),则点B2020的坐标是什么?
19.
如图:四边形ABCD为矩形,H、F分别为AD、BC的中点,四边形EFGH为矩形.E、G分别在AB、CD边上,则图中四个直角三角形面积之和与矩形EFGH面积之间的关系是什么?并加以证明你的结论.(8分)
20.
我们学校举行歌咏比赛,组委规定任何一名参赛选手成绩满足赛后整理所有参赛选手的成绩如右表:(6分)
请求出、.
21.
已知如图:矩形ABCD中,AB=4,BC=2.点E、F分别在AB、CD上,且BE=DF=.(8分)
(1)证明:四边形AECF是菱形.
(2)求EF的长度.
22.
如图直线∶和相交于点P(,),与轴交于点A.
与轴交于点B.(8分)
(1)求直线的表达式.
(2)求△ABP的面积.
23.
如图,矩形ABCD中,AB=8,AD=6。点O是对角线BD的中点,过点O的直线分别交AB、CD边于点E、F.(10分)
(1)求证:四边形DEBF是平行四边形.
(2)当DE=DF时,求EF.
24.
如图:△ABC是边长为3cm的等边三角形动点P、Q同时从A、B两点出发,分别沿AB、BC方向匀速移动,它们的速度都是1cm/s,当点P到达B时,P、Q两点停止运动,设点P到达B时,P、Q两点停止运动.设点P运动的时间为t(s).当t为何值时,△PBQ是直角三角形?(10分)
25.
学校为了美化环境,计划分两次购进A、B两种花.(两次价格相同)(12分)
(1)求A、B两种花的单价?
(2)若购买A、B两种花共31棵,且B种
花的数量不大于A种花的数量的2倍.
请给出一种费用最省的方案,并求出该方案所需费用.
26.
将一个直角三角形纸片ABO放置在平面直角坐标系中,点A(,0),点B(0,1),P是边AB上的一点(点P不与A、B重合)沿着P折叠该纸片得点的对应点A′.
(1)如图①当点A′在第一象限,且满足A′B⊥OB时,求A′的坐标.
(2)如图②当P为AB的中点时,求A′B的长.
2020年上期八年级期末质量监测卷
数学参考答案
一、选择题:1——10:C
B
D
D
B
D
B
A
A
A
二、填空:11.(-4,3)
12.
8
13.
0.1
14.
2
15.略(符合题意即可)
16.
三、17.
利用H、L定理证得
18.
利用勾股定理计算:B2(6,2)
B4(12,2)……B2020(6×1010,2)即B2020(6060,2)
19.
相等,提示,连HF利用等底同高,面积相等或其它方法可。
20.
21.
(1)计算后,知AECF为菱形
(2)连AC,则AC=2,∴
22.(1)
(2)与轴交点C(-1,0)
23.
(1)结论成立
(2)DO==5,∵DE=DF,四边形DEBF是菱形,设AE=,则DE=,
∴,∴
24.
(1)
∵,另一情况:
∴当或2时,△PBQ是Rt△.
25.
(1)设A、B两花单价为、,则
(2)要费用最省,需最小且、自然数,∴时,符合题意,费用11×20+20×5=320元
26.
(1)∵A()B(0,1)由对叠可知OA′=OA=,∴A′B=
∴A′(,1)
(2)∵P是中点,AB=,∴OP=为等边三角形,又根据对叠的性质,A′P=AP=1=OB,∠BOA′=60°-∠A′OP=60°-∠POA=30°=∠OAP=∠OA′P=30°A′P∥OB四边形OPA′B是□,∴A′B=OP=1.
(在Rt△AOB中,∠OAB=30°)
分数段
频数
频率
30
0.15
0.45
60
20
0.1
A
B
开支
一次
30
15
675
二次
12
5
265
PAGE
2020年上期八年级期末质量监测(数学)
第1页(共4页)
同课章节目录
