2021-2022学年北师大版数学九年级上册4.7相似三角形的性质课件(18张ppt)
文档属性
| 名称 | 2021-2022学年北师大版数学九年级上册4.7相似三角形的性质课件(18张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-07 13:47:06 | ||
图片预览



文档简介
(共18张PPT)
第四章
图形的相似
4.7相似三角形的性质
1.什么叫做相似三角形?
2.你有几种方法判定两个三角形是相似三角形?
三角分别相等、三边成比例的两个三角形叫做相似三
角形.
(1)两角分别相等的两个三角形相似.
(2)两边成比例且夹角相等的两个三角形相似.
(3)三边成比例的两个三角形相似.
1.探索相似三角形的性质.
2.发展学生合情推理和有条理的表达能力.
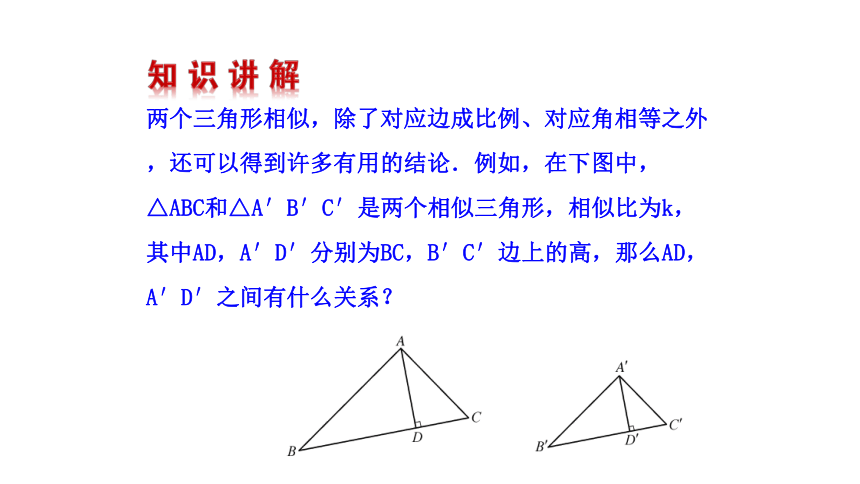
两个三角形相似,除了对应边成比例、对应角相等之外,还可以得到许多有用的结论.例如,在下图中,△ABC和△A′B′C′是两个相似三角形,相似比为k,其中AD,A′D′分别为BC,B′C′边上的高,那么AD,A′D′之间有什么关系?
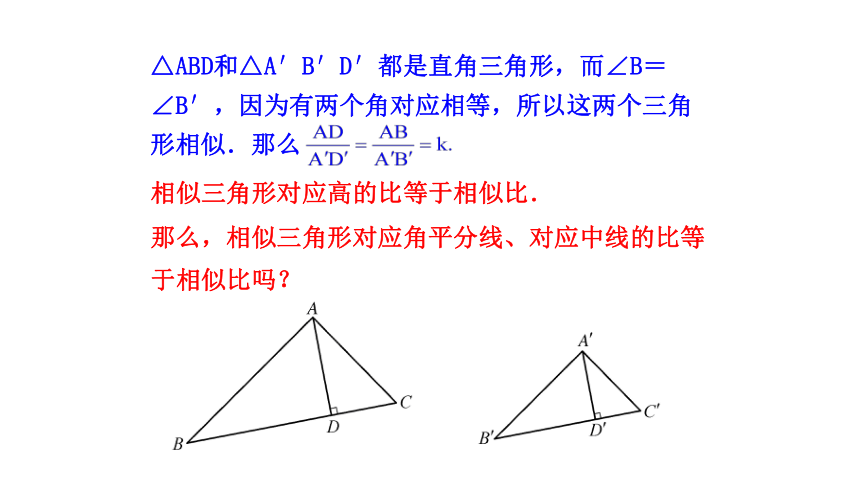
△ABD和△A′B′D′都是直角三角形,而∠B=
∠B′,因为有两个角对应相等,所以这两个三角
形相似.那么
相似三角形对应高的比等于相似比.
那么,相似三角形对应角平分线、对应中线的比等于相似比吗?
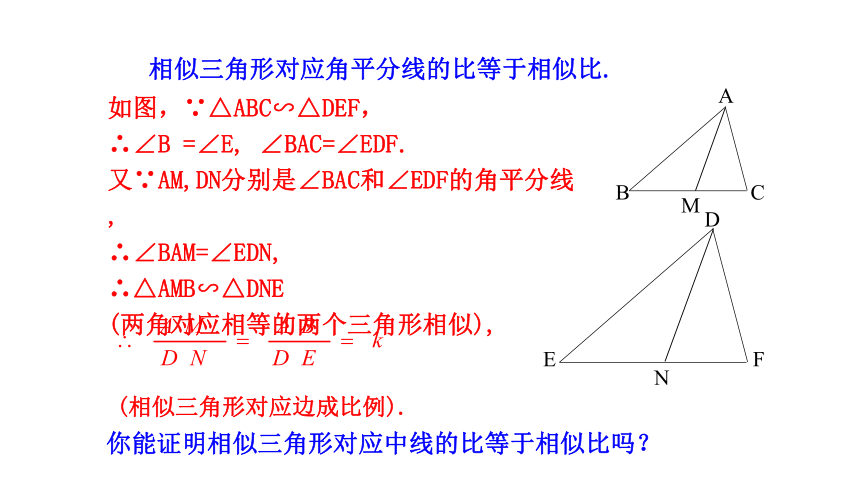
如图,∵△ABC∽△DEF,
∴∠B
=∠E,
∠BAC=∠EDF.
又∵AM,DN分别是∠BAC和∠EDF的角平分线,
∴∠BAM=∠EDN,
∴△AMB∽△DNE
(两角对应相等的两个三角形相似),
相似三角形对应角平分线的比等于相似比.
(相似三角形对应边成比例).
A
B
C
M
D
E
F
N
你能证明相似三角形对应中线的比等于相似比吗?
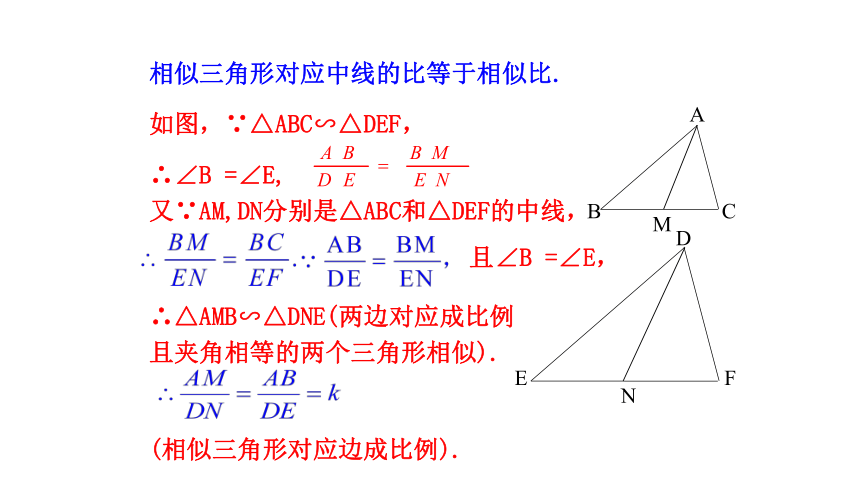
如图,∵△ABC∽△DEF,
∴∠B
=∠E,
相似三角形对应中线的比等于相似比.
(相似三角形对应边成比例).
A
B
C
M
D
E
F
N
又∵AM,DN分别是△ABC和△DEF的中线,
∴△AMB∽△DNE(两边对应成比例且夹角相等的两个三角形相似).
且∠B
=∠E,
定理:相似三角形对应高的比、对应角平分线的比、对应中线的比都等于相似比.
相似三角形的性质
如果△ABC和△A′B′C′是两个相似三角形,相似比为k,那么
由等比性质,得
定理:相似三角形的周长比等于相似比.
相似三角形的面积比与相似比有什么关系?
如果△ABC和△A′B′C′是两个相似三角形,相似比为k,高为AD,A′D′,那么
根据三角形的面积计算公式及有关定理,得
定理:相似三角形的面积比等于相似比的平方.
下图中(1)、(2)、(3)分别是边长为1,2,3的等边三角形,它们都相似.
(2)与(1)的相似比=_______,
(2)与(1)的面积比=_______,
(3)与(1)的相似比=_______,
(3)与(1)的面积比=_______.
2:1
4:1
3:1
9:1
【例题】
1.如果两个三角形相似,相似比为3∶5,那么对应
角平分线的比等于多少?______.
2.相似三角形对应边的比为0.4,那么相似比为
______,
对应角平分线的比为______,周长的比为______,
面积的比为______.
3∶5
0.4
0.4
0.16
3.若两个三角形面积之比为16:9,则它们的对应
高之比为________,对应中线之比为________.
4:3
4:3
0.4
【跟踪训练】
掌握相似三角形的性质:
(1)对应角相等,对应边成比例.
(2)相似三角形对应高的比,对应角平分线的比,对应中线的比都等于相似比.
(3)相似三角形的周长比等于相似比.
(4)相似三角形的面积比等于相似比的平方.
1.(2021?济宁质检)两个相似三角形对应中线的长分别
为6cm和12cm,若较大三角形的面积是12cm2,则较小的
三角形的面积为( )
.
A.1
B.3
C.4
D.6
B
2.(2021?鄞州质检)如图,已知△ABC∽△BDC,其中AC=4,CD=2,则BC=( )
A.2
B.
C.
D.4
B
3.(2021?湖南期末)已知△ABC∽△DEF,若∠A=30°,∠E=70°,则∠F的度数为( )
A.30°
B.70°
C.80°
D.120°
C
4.(2021?西林县期末)已知△ABC∽△DEF,且面积比为1:9,若△ABC的周长为8cm,则△DEF的周长是
cm.
【考点】相似三角形的性质.
【专题】图形的相似;数据分析观念.
24
5.(2021?南京期末)如图,△ABC∽△A′B′C′,AD,A′D′分别是它们的中线,求证:AD:A′D′=AB:A′B′.
证明:∵AD,A′D′分别是△ABC和△A′B′C′的中线,
∵△ABC∽△A′B′C′,
∴△ABD∽△A′B′D′,
∴AD:A′D′=AB:A′B′.
6.(2021?武侯质检)已知:如图,Rt△ABC∽Rt△ACD,若AC=3,BC=4,求AD.
解:∵AC=3,BC=4,∠ACB=90°,
由勾股定理得:AB=5,
∵Rt△ABC∽Rt△ACD,
第四章
图形的相似
4.7相似三角形的性质
1.什么叫做相似三角形?
2.你有几种方法判定两个三角形是相似三角形?
三角分别相等、三边成比例的两个三角形叫做相似三
角形.
(1)两角分别相等的两个三角形相似.
(2)两边成比例且夹角相等的两个三角形相似.
(3)三边成比例的两个三角形相似.
1.探索相似三角形的性质.
2.发展学生合情推理和有条理的表达能力.
两个三角形相似,除了对应边成比例、对应角相等之外,还可以得到许多有用的结论.例如,在下图中,△ABC和△A′B′C′是两个相似三角形,相似比为k,其中AD,A′D′分别为BC,B′C′边上的高,那么AD,A′D′之间有什么关系?
△ABD和△A′B′D′都是直角三角形,而∠B=
∠B′,因为有两个角对应相等,所以这两个三角
形相似.那么
相似三角形对应高的比等于相似比.
那么,相似三角形对应角平分线、对应中线的比等于相似比吗?
如图,∵△ABC∽△DEF,
∴∠B
=∠E,
∠BAC=∠EDF.
又∵AM,DN分别是∠BAC和∠EDF的角平分线,
∴∠BAM=∠EDN,
∴△AMB∽△DNE
(两角对应相等的两个三角形相似),
相似三角形对应角平分线的比等于相似比.
(相似三角形对应边成比例).
A
B
C
M
D
E
F
N
你能证明相似三角形对应中线的比等于相似比吗?
如图,∵△ABC∽△DEF,
∴∠B
=∠E,
相似三角形对应中线的比等于相似比.
(相似三角形对应边成比例).
A
B
C
M
D
E
F
N
又∵AM,DN分别是△ABC和△DEF的中线,
∴△AMB∽△DNE(两边对应成比例且夹角相等的两个三角形相似).
且∠B
=∠E,
定理:相似三角形对应高的比、对应角平分线的比、对应中线的比都等于相似比.
相似三角形的性质
如果△ABC和△A′B′C′是两个相似三角形,相似比为k,那么
由等比性质,得
定理:相似三角形的周长比等于相似比.
相似三角形的面积比与相似比有什么关系?
如果△ABC和△A′B′C′是两个相似三角形,相似比为k,高为AD,A′D′,那么
根据三角形的面积计算公式及有关定理,得
定理:相似三角形的面积比等于相似比的平方.
下图中(1)、(2)、(3)分别是边长为1,2,3的等边三角形,它们都相似.
(2)与(1)的相似比=_______,
(2)与(1)的面积比=_______,
(3)与(1)的相似比=_______,
(3)与(1)的面积比=_______.
2:1
4:1
3:1
9:1
【例题】
1.如果两个三角形相似,相似比为3∶5,那么对应
角平分线的比等于多少?______.
2.相似三角形对应边的比为0.4,那么相似比为
______,
对应角平分线的比为______,周长的比为______,
面积的比为______.
3∶5
0.4
0.4
0.16
3.若两个三角形面积之比为16:9,则它们的对应
高之比为________,对应中线之比为________.
4:3
4:3
0.4
【跟踪训练】
掌握相似三角形的性质:
(1)对应角相等,对应边成比例.
(2)相似三角形对应高的比,对应角平分线的比,对应中线的比都等于相似比.
(3)相似三角形的周长比等于相似比.
(4)相似三角形的面积比等于相似比的平方.
1.(2021?济宁质检)两个相似三角形对应中线的长分别
为6cm和12cm,若较大三角形的面积是12cm2,则较小的
三角形的面积为( )
.
A.1
B.3
C.4
D.6
B
2.(2021?鄞州质检)如图,已知△ABC∽△BDC,其中AC=4,CD=2,则BC=( )
A.2
B.
C.
D.4
B
3.(2021?湖南期末)已知△ABC∽△DEF,若∠A=30°,∠E=70°,则∠F的度数为( )
A.30°
B.70°
C.80°
D.120°
C
4.(2021?西林县期末)已知△ABC∽△DEF,且面积比为1:9,若△ABC的周长为8cm,则△DEF的周长是
cm.
【考点】相似三角形的性质.
【专题】图形的相似;数据分析观念.
24
5.(2021?南京期末)如图,△ABC∽△A′B′C′,AD,A′D′分别是它们的中线,求证:AD:A′D′=AB:A′B′.
证明:∵AD,A′D′分别是△ABC和△A′B′C′的中线,
∵△ABC∽△A′B′C′,
∴△ABD∽△A′B′D′,
∴AD:A′D′=AB:A′B′.
6.(2021?武侯质检)已知:如图,Rt△ABC∽Rt△ACD,若AC=3,BC=4,求AD.
解:∵AC=3,BC=4,∠ACB=90°,
由勾股定理得:AB=5,
∵Rt△ABC∽Rt△ACD,
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
