2021—2022学年冀教版数学八年级上册 17.1等腰三角形课件(32张ppt)
文档属性
| 名称 | 2021—2022学年冀教版数学八年级上册 17.1等腰三角形课件(32张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-07 13:48:27 | ||
图片预览







文档简介
(共32张PPT)
等腰三角形
17.1
欣赏生活中的三角形
欣赏生活中的三角形
欣赏生活中的三角形
从生活走进数学
这些三角形有什么共同特点呢?
它们是否具有一般三角形所不具备的特有的性质?
从生活走进数学
这些从实际物体中抽象出来的三角形,具备怎样的共同特点?
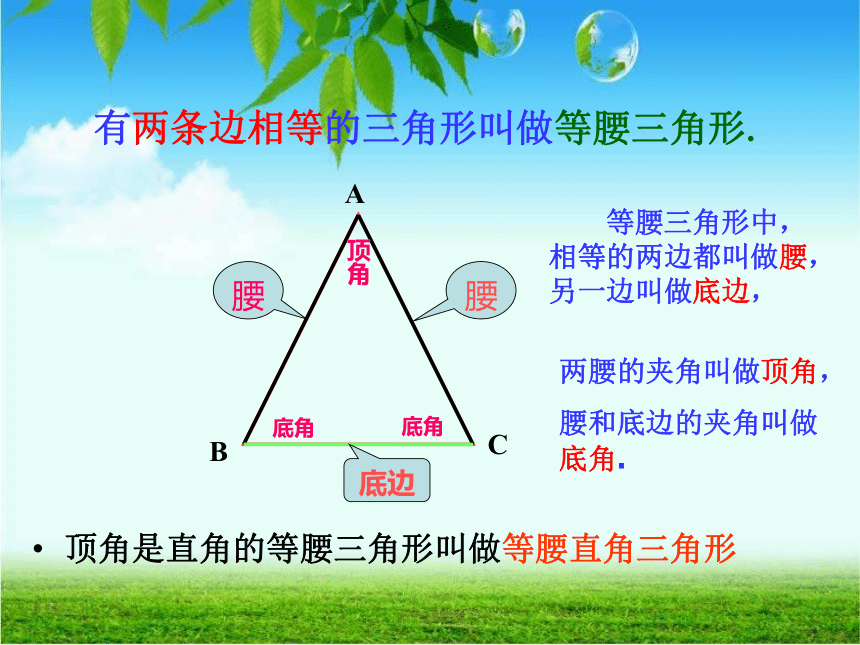
有两条边相等的三角形叫做等腰三角形.
等腰三角形中,相等的两边都叫做腰,另一边叫做底边,
A
C
B
腰
腰
底边
顶角
底角
底角
两腰的夹角叫做顶角,
腰和底边的夹角叫做底角.
顶角是直角的等腰三角形叫做等腰直角三角形
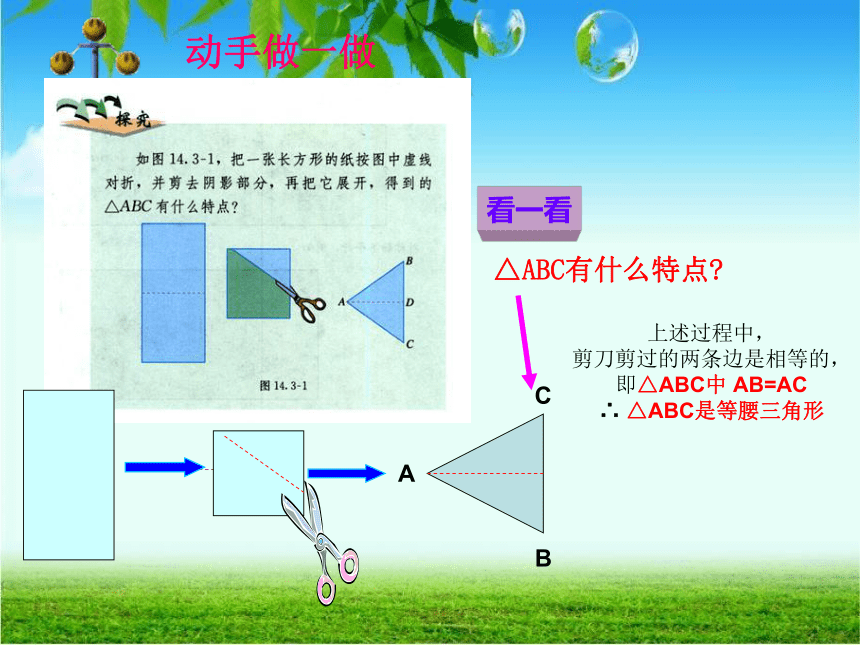
动手做一做
A
C
B
△ABC有什么特点?
看一看
上述过程中,
剪刀剪过的两条边是相等的,
即△ABC中
AB=AC
∴
△ABC是等腰三角形
探究:
把剪出的等腰三角形ABC沿折痕对折,找出其中重合的线段和角.
找一找
由这些重合的线段和角,你能发现等腰三角形的性质吗?说说你的猜想。
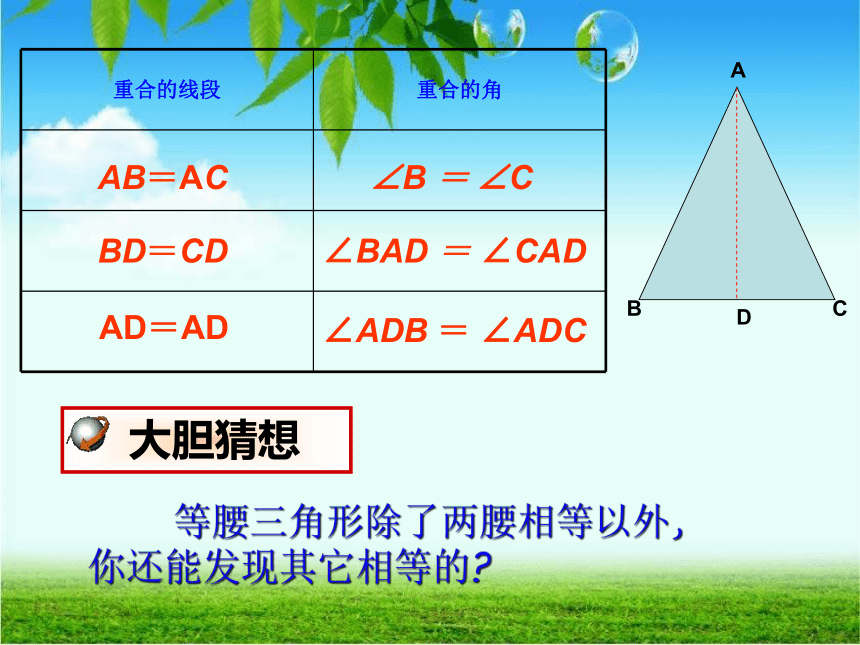
重合的线段
重合的角
A
C
B
D
AB=AC
BD=CD
AD=AD
∠B
=
∠C
∠BAD
=
∠CAD
∠ADB
=
∠ADC
等腰三角形除了两腰相等以外,
你还能发现其它相等的?
大胆猜想
猜想与论证一:
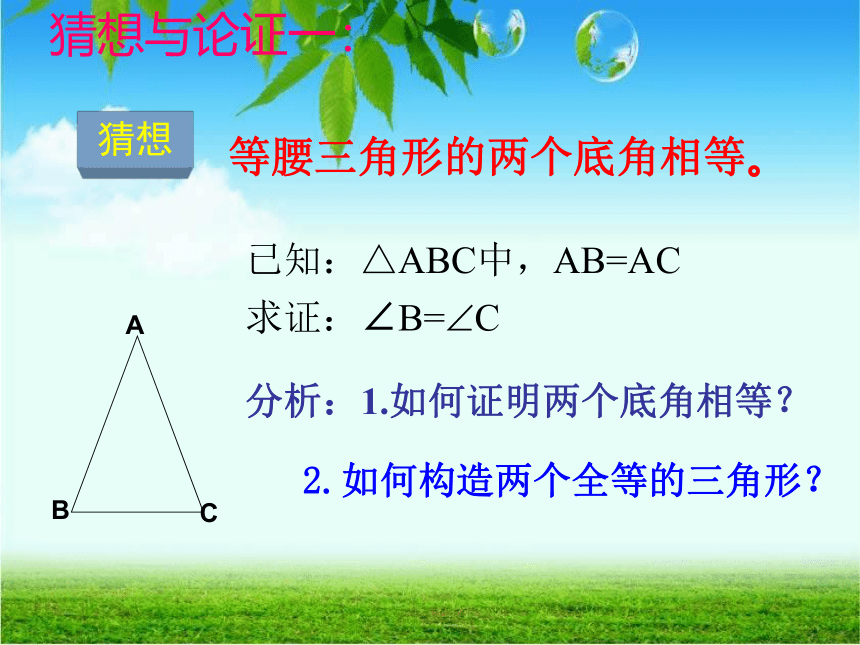
等腰三角形的两个底角相等。
已知:△ABC中,AB=AC
求证:∠B=?C
分析:1.如何证明两个底角相等?
2.如何构造两个全等的三角形?
A
B
C
猜想
A
B
C
则有∠1=∠2
D
1
2
在△ABD和△ACD中
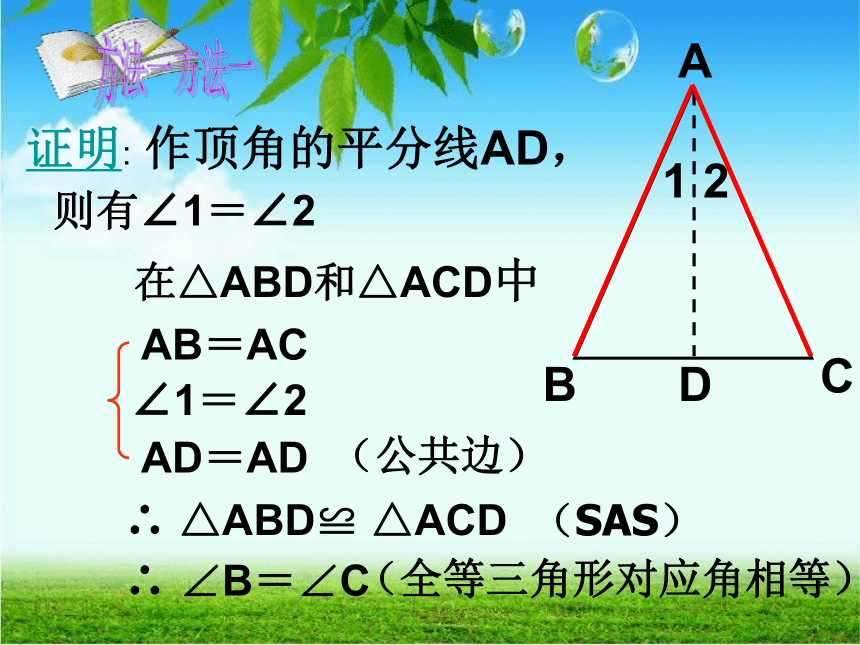
证明:
作顶角的平分线AD,
AB=AC
∠1=∠2
AD=AD
(公共边)
∴
△ABD≌
△ACD
(SAS)
∴
∠B=∠C
(全等三角形对应角相等)
方法一
A
B
C
则有
BD=CD
D
在△ABD和△ACD中
证明:
作△ABC
的中线AD
AB=AC
BD=CD
AD=AD
(公共边)
∴
△ABD≌
△ACD
(SSS)
∴
∠B=∠C
(全等三角形对应角相等)
方法二
A
B
C
D
证明:
作△ABC
的高线AD
方法三
等腰三角形性质
性质1:
等腰三角形两个底角相等,
简称“等边对等角”
在△ABC中,∵
AB=AC
∴
=
,
数学语言
∠B
∠C
A
B
C
A
B
C
则有∠1=
∠2
D
1
2
在△ABD和△ACD中
证明:
作顶角的平分线AD,
AB=AC
∠1=∠2
AD=AD
(公共边)
∴
△ABD≌
△ACD
(SAS)
∴
∠B=∠C
(全等三角形对应角相等)
在刚才的证明过程中你还能得到其它的结论吗?
A
B
C
D
等腰三角形性质
性质2
等腰三角形的顶角平分线、底边
上的中线、底边上的高互相重合。
(可简记为“三线合一”)
性质2:在△ABC中,
(
1
)
∵
AB=AC
AD是角平分线,
∴
⊥
,
____=_____
;
(
2
)
∵
AB=AC
AD是中线,
∴
⊥
,∴∠
=
∠____;
(
3
)
∵
AB=AC
AD⊥BC,
∴∠_____=∠______,_____=______
。
BAD
CAD
BAD
CAD
AD
BC
AD
BC
BD
CD
BD
CD
数学语言
等腰三角形是轴对称图形,对称轴是什么?
思考
※等腰三角形是轴对称图形,底边上的中线
(顶角平分线,底边上的高)所在的直线就是
它的对称轴。
A
B
P
l
A
A
B
┌
作△ABC的高AD.
D
C
B
C
等腰三角形常见辅助线
1
作顶角的平分线AD.
D
2
A
B
C
作△ABC底边BC的中线AD.
D
等腰三角形的性质定理:
等腰三角形的两个底角相等。(简称“等边对等角”)
等腰三角形的顶角平分线、底边上的中线、底边上的高重合。(简称“三线合一”)
归纳与概括
(1)已知等腰三形的一个顶角为36°,则它的两个底角分别为
。
(3)已知等腰三角形的一个角为40°则其它两个内角分别为
。
(4)已知等腰三角形的一个角为110°,则其它的两个内角分别为
。
72°
、72°
70°
、70°,
40°
、100°
35°
、35°
(2)已知等腰三形的一个底角为36°,则它的两个内角分别为
。
36o
,108o
应用与提高
已知等腰三角形的一个内角的度数,求其它两角时,
(a)①
顶角度数+2×底角度数=180°
②
0°<顶角度数<180°
③
0°<底角度数<90°
(b)若已知角为钝角或直角,则它一定是顶角;
(c)若已知角为锐角,它可能是顶角,也可能是底角.
归纳总结
分类讨论
例1
:如图△ABC是一个屋顶的平面示意图,已知屋椽AB=AC,立柱AD⊥BC,底角∠B=40°,梁长BC=10米,则顶架上∠CAD=______度,BD=_____米.
A
B
C
D
延
伸
与
拓
展
50
5
例2:
如图,在△ABC中,
AB=AC,BD,CE
分别为∠ABC,∠ACB
的平分线。
求证:BD=CE.
A
B
C
D
E
延
伸
与
拓
展
延
伸
与
拓
展
A
B
C
D
E
证明:
∵BD,CE
分别为∠ABC,∠ACB
的平分线,
∴
∠ABD=
∠ABC,
∠ACE=
∠ACB
(角平分线的定义)
∵
AB=AC(已知)
∴
∠ABC=∠ACB
(等边对等角)
∴
∠ABD=
∠ACE(等量代换)
在△ABD和
△
ACE中
∠A=
∠A(公共角)
AB=AC(已知)
∠ABD=
∠ACE(已证)
∴
△ABD≌
△
ACE(ASA)
∴BD=CE(全等三角形对应边相等)
2
1
2
1
三边都相等的三角形叫做等边三角形。
等边三角形是等腰三角形的特例。
等边三角形的边和角又分别有怎样的关系呢?为什么?
能证明你发现的命题吗?
猜
想
与
证
明
A
B
C
已知:如图,在△ABC中,AB=BC
=
AC.
求证:
∠A=
∠B=∠C=60°.
等边三角形的性质定理:
等边三角形的三个角都相等,并且每一个角都等于60°.
应用与提高
如图,△ABC是等边三角形,D是BC的中点,点E在AC上,且AE=AD,求∠EDC
(等边对等角)
(三线合一)
解:
(等边三角形每一个角都是60°)
回
顾
与
反
思
这节课我们研究了哪些问题?
我们在研究这些问题时,经历了怎样的过程?
通过这个研究过程,你有什么感受和体会?
等腰三角形是轴对称图形,底边上的中线(顶角平分线,底边上的高)所在的直线就是它的对称轴。
性质1:等腰三角形两个底角相等,简称“等边对等角”(前提是在同一个三角形中。)
性质2
:等腰三角形的顶角的角平分线、底边上的中线、和底边上的高互相重合,简称“三线合
一”(前提是在同一个等腰三角形中。)
等腰三角形
小
结
等边三角形的性质定理:
等边三角形的三个角都相等,并且每一个角都等于60°
作业
中午作业:课本第143页,
A组
1、3题.
晚上作业:《同步》17.1等腰三角形(一)
去掉第8题。
谢谢大家
等腰三角形
17.1
欣赏生活中的三角形
欣赏生活中的三角形
欣赏生活中的三角形
从生活走进数学
这些三角形有什么共同特点呢?
它们是否具有一般三角形所不具备的特有的性质?
从生活走进数学
这些从实际物体中抽象出来的三角形,具备怎样的共同特点?
有两条边相等的三角形叫做等腰三角形.
等腰三角形中,相等的两边都叫做腰,另一边叫做底边,
A
C
B
腰
腰
底边
顶角
底角
底角
两腰的夹角叫做顶角,
腰和底边的夹角叫做底角.
顶角是直角的等腰三角形叫做等腰直角三角形
动手做一做
A
C
B
△ABC有什么特点?
看一看
上述过程中,
剪刀剪过的两条边是相等的,
即△ABC中
AB=AC
∴
△ABC是等腰三角形
探究:
把剪出的等腰三角形ABC沿折痕对折,找出其中重合的线段和角.
找一找
由这些重合的线段和角,你能发现等腰三角形的性质吗?说说你的猜想。
重合的线段
重合的角
A
C
B
D
AB=AC
BD=CD
AD=AD
∠B
=
∠C
∠BAD
=
∠CAD
∠ADB
=
∠ADC
等腰三角形除了两腰相等以外,
你还能发现其它相等的?
大胆猜想
猜想与论证一:
等腰三角形的两个底角相等。
已知:△ABC中,AB=AC
求证:∠B=?C
分析:1.如何证明两个底角相等?
2.如何构造两个全等的三角形?
A
B
C
猜想
A
B
C
则有∠1=∠2
D
1
2
在△ABD和△ACD中
证明:
作顶角的平分线AD,
AB=AC
∠1=∠2
AD=AD
(公共边)
∴
△ABD≌
△ACD
(SAS)
∴
∠B=∠C
(全等三角形对应角相等)
方法一
A
B
C
则有
BD=CD
D
在△ABD和△ACD中
证明:
作△ABC
的中线AD
AB=AC
BD=CD
AD=AD
(公共边)
∴
△ABD≌
△ACD
(SSS)
∴
∠B=∠C
(全等三角形对应角相等)
方法二
A
B
C
D
证明:
作△ABC
的高线AD
方法三
等腰三角形性质
性质1:
等腰三角形两个底角相等,
简称“等边对等角”
在△ABC中,∵
AB=AC
∴
=
,
数学语言
∠B
∠C
A
B
C
A
B
C
则有∠1=
∠2
D
1
2
在△ABD和△ACD中
证明:
作顶角的平分线AD,
AB=AC
∠1=∠2
AD=AD
(公共边)
∴
△ABD≌
△ACD
(SAS)
∴
∠B=∠C
(全等三角形对应角相等)
在刚才的证明过程中你还能得到其它的结论吗?
A
B
C
D
等腰三角形性质
性质2
等腰三角形的顶角平分线、底边
上的中线、底边上的高互相重合。
(可简记为“三线合一”)
性质2:在△ABC中,
(
1
)
∵
AB=AC
AD是角平分线,
∴
⊥
,
____=_____
;
(
2
)
∵
AB=AC
AD是中线,
∴
⊥
,∴∠
=
∠____;
(
3
)
∵
AB=AC
AD⊥BC,
∴∠_____=∠______,_____=______
。
BAD
CAD
BAD
CAD
AD
BC
AD
BC
BD
CD
BD
CD
数学语言
等腰三角形是轴对称图形,对称轴是什么?
思考
※等腰三角形是轴对称图形,底边上的中线
(顶角平分线,底边上的高)所在的直线就是
它的对称轴。
A
B
P
l
A
A
B
┌
作△ABC的高AD.
D
C
B
C
等腰三角形常见辅助线
1
作顶角的平分线AD.
D
2
A
B
C
作△ABC底边BC的中线AD.
D
等腰三角形的性质定理:
等腰三角形的两个底角相等。(简称“等边对等角”)
等腰三角形的顶角平分线、底边上的中线、底边上的高重合。(简称“三线合一”)
归纳与概括
(1)已知等腰三形的一个顶角为36°,则它的两个底角分别为
。
(3)已知等腰三角形的一个角为40°则其它两个内角分别为
。
(4)已知等腰三角形的一个角为110°,则其它的两个内角分别为
。
72°
、72°
70°
、70°,
40°
、100°
35°
、35°
(2)已知等腰三形的一个底角为36°,则它的两个内角分别为
。
36o
,108o
应用与提高
已知等腰三角形的一个内角的度数,求其它两角时,
(a)①
顶角度数+2×底角度数=180°
②
0°<顶角度数<180°
③
0°<底角度数<90°
(b)若已知角为钝角或直角,则它一定是顶角;
(c)若已知角为锐角,它可能是顶角,也可能是底角.
归纳总结
分类讨论
例1
:如图△ABC是一个屋顶的平面示意图,已知屋椽AB=AC,立柱AD⊥BC,底角∠B=40°,梁长BC=10米,则顶架上∠CAD=______度,BD=_____米.
A
B
C
D
延
伸
与
拓
展
50
5
例2:
如图,在△ABC中,
AB=AC,BD,CE
分别为∠ABC,∠ACB
的平分线。
求证:BD=CE.
A
B
C
D
E
延
伸
与
拓
展
延
伸
与
拓
展
A
B
C
D
E
证明:
∵BD,CE
分别为∠ABC,∠ACB
的平分线,
∴
∠ABD=
∠ABC,
∠ACE=
∠ACB
(角平分线的定义)
∵
AB=AC(已知)
∴
∠ABC=∠ACB
(等边对等角)
∴
∠ABD=
∠ACE(等量代换)
在△ABD和
△
ACE中
∠A=
∠A(公共角)
AB=AC(已知)
∠ABD=
∠ACE(已证)
∴
△ABD≌
△
ACE(ASA)
∴BD=CE(全等三角形对应边相等)
2
1
2
1
三边都相等的三角形叫做等边三角形。
等边三角形是等腰三角形的特例。
等边三角形的边和角又分别有怎样的关系呢?为什么?
能证明你发现的命题吗?
猜
想
与
证
明
A
B
C
已知:如图,在△ABC中,AB=BC
=
AC.
求证:
∠A=
∠B=∠C=60°.
等边三角形的性质定理:
等边三角形的三个角都相等,并且每一个角都等于60°.
应用与提高
如图,△ABC是等边三角形,D是BC的中点,点E在AC上,且AE=AD,求∠EDC
(等边对等角)
(三线合一)
解:
(等边三角形每一个角都是60°)
回
顾
与
反
思
这节课我们研究了哪些问题?
我们在研究这些问题时,经历了怎样的过程?
通过这个研究过程,你有什么感受和体会?
等腰三角形是轴对称图形,底边上的中线(顶角平分线,底边上的高)所在的直线就是它的对称轴。
性质1:等腰三角形两个底角相等,简称“等边对等角”(前提是在同一个三角形中。)
性质2
:等腰三角形的顶角的角平分线、底边上的中线、和底边上的高互相重合,简称“三线合
一”(前提是在同一个等腰三角形中。)
等腰三角形
小
结
等边三角形的性质定理:
等边三角形的三个角都相等,并且每一个角都等于60°
作业
中午作业:课本第143页,
A组
1、3题.
晚上作业:《同步》17.1等腰三角形(一)
去掉第8题。
谢谢大家
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
